前回は「3つのてんびん算の仕組みとポイント〜「混ぜて半分」を描いて理解・図解してポイントを見つける・「混ぜて半分」の食塩水・食塩と水の正体・食塩水と食塩と水の算数的視点・問題 12解法〜」の話でした。
問題 12
文章題の流れを図解して理解：大事なポイントと量
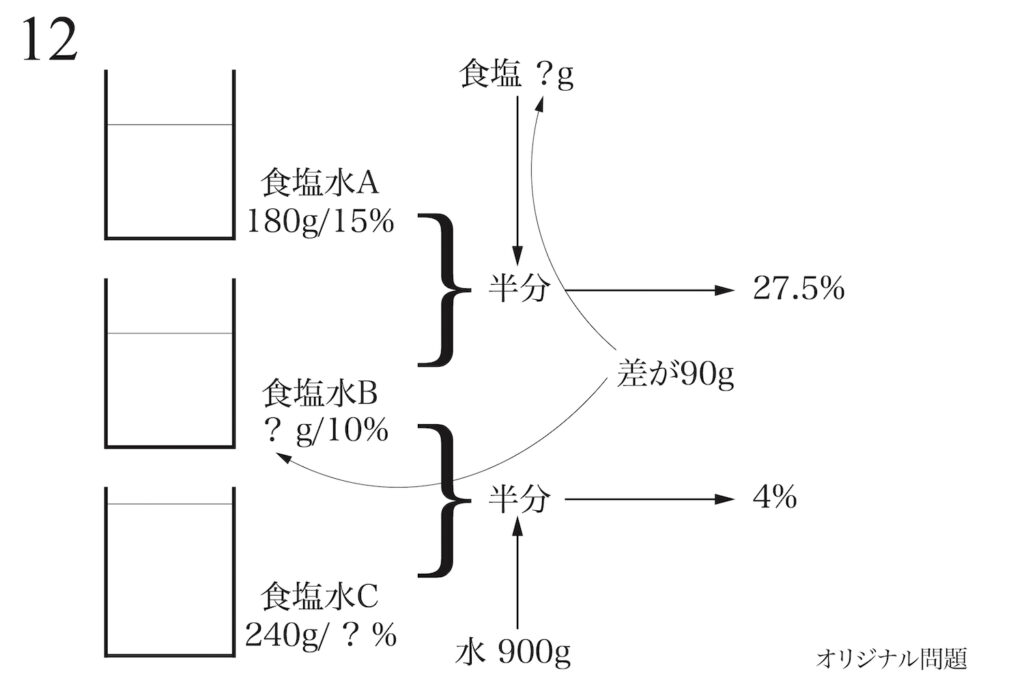
食塩水が2つであることが多い、食塩水の問題。
今回は食塩水が3つ登場し、さらに「混ぜて半分」にして、その後、食塩・水を加えます。
プロセスが複雑なので「難しく見える」のですが、プロセスを上のように絵で描いてみましょう。
男子小学生問題文読めば、
分かるよ。
文章を読めば、「内容は分かる」と思います。
上のように、「状況を整理する」と見えてくることがあります。
・状況を簡単な絵や図に描く
・状況をしっかり理解することが解く第一歩
・大事な量・長さなどを見落とさない
対象が3つになると「難しく感じられる」のは、理科の電気・電流の話と同じです。
電流・電圧・抵抗の三つも登場する電気の問題は、「考える対象が多いので難しい」のです。
上記リンクでは、電気の問題で「主役は電圧」と考える話をご紹介しています。
電気・電流では「主役は電圧」でしたが、食塩水の問題では「主役は濃度と重さ」です。
この「濃度と重さ」のどちらかが優先されることが多いです。
てんびん算でも方程式で考えても、「濃度と重さは同等に扱う」ことが多いです。
・食塩水の濃度は0%から100%まで連続的に変化する
・塩は「濃度100%の食塩水」で（真）水は「濃度0%の食塩水」
「食塩があるから食塩水になる」という意味では、「濃度」がやや重要性が高いと考えます。
・電気の問題：主役は電圧
・食塩水の問題：主役は濃度（重さの時もある）
こういう「複雑に見える」問題で、問題文を読んで「すぐ解き始める」のはやめましょう。
とても算数が得意な方は、「すぐ解き始める」でも良いかもしれません。
上のように状況を整理することは、「問題を解く・考える第一歩」で非常に大事な姿勢です。
数学や物理（算数・理科）を考えるとき、最も大事なことは「状況把握」です。
上のような状況の図を描いただけでも、記述式の学校なら「何点か入る可能性」があります。
男子小学生でも、これだと、
何も解いてないよ・・・
確かに「解いてない」のですが、「状況把握」の大事な姿勢が伺えます。
採点者からすると、「図や絵を描いて理解する姿勢」は非常に好ましいのです。
このような絵が描かれていると、採点者は、
採点者問題を
よく理解しているな・・・
このように考えて、解くのが途中で終わっていても、
採点者ここまでは、
よく出来ている・・・
「ここまではOK」として、ある程度の点数を与えるでしょう。
記述タイプの出題で、比較的大きな解答欄がある場合は、上のような図を必ず描きましょう。
例えば、武蔵中の場合は上の図だけで何も進んでいなくても、必ず1点以上加点されます。
武蔵中に合格するための秘訣を、上記リンクでご紹介しています。
それぞれの学校にも様々なカラーがありますが、武蔵は「自分で考えること」を最重視します。
また、記述タイプの問題の解き方や考え方を上記リンクでご紹介しています。
「知識がある」や「テクニックがある」ことは「自分で考えること」より「遥かに劣ること」です。
採点者「知っていること」よりも、
「自分で考えること」が大事！
こういう発想・教育理念を持つ学校が武蔵中学校・高校です。
そこが武蔵中高の武蔵中高たる所以であり、アカデミックな学校である点です。
武蔵中高の校長を務めた山川健次郎の話を、上記リンクでご紹介しています。
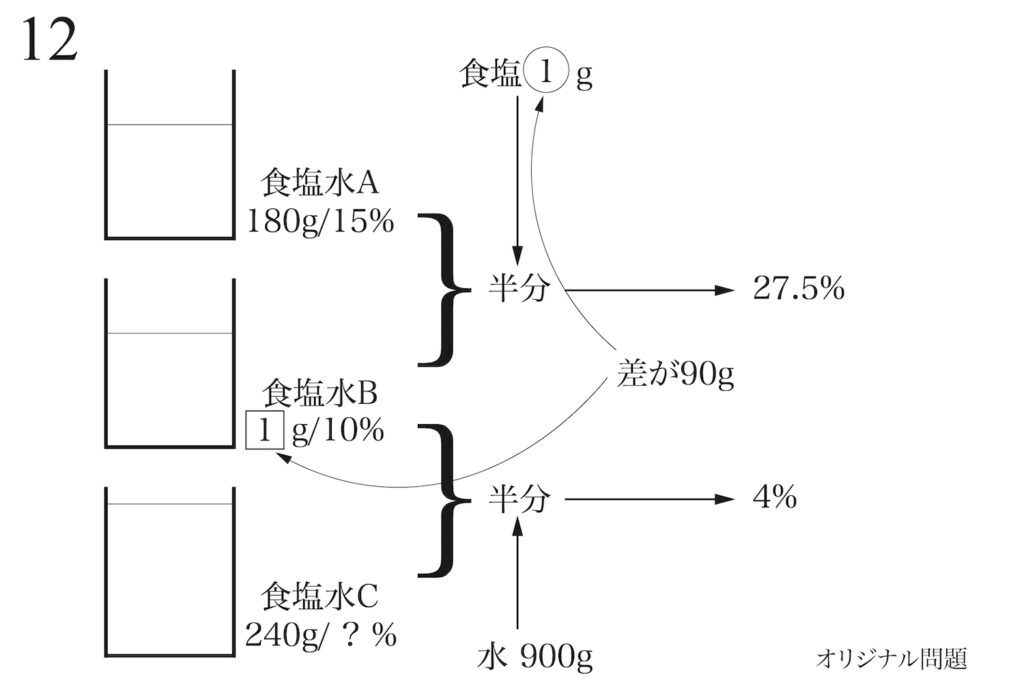
上のように状況を描きましたが、「？%」などでは進みませんので、未知数を設置しましょう。
分からないモノが3つありますが、まずは食塩水Bの重さ、AとBに加える食塩の重さを未知数でおきます。
考える対象を3つから2つへ絞る
女子小学生「混ぜて半分」が「半分にして混ぜる」ことと
同じなのは分かったけど・・・
女子小学生食塩水が3つもあると、
分からなくなってしまう・・・
ここで、食塩水Cの濃度は後回しにします。
女子小学生でも、解かなければ
ならないでしょ？
「食塩水Bの重さ」と「AとBに加える食塩」のみ先に考えることにした理由があります。
それは、「これらの差が90g」があるからです。
食塩水のプロセスから、これら二つの関係式が出てきます。
そして、「これらの差が90g」の条件から、
女子小学生この二つは
分かりそうだ！
このように考えると良いでしょう。
この問題が「難しく見える」理由は、プロセスが複雑なのと、「分からないモノが3つある」ことです。
電気・電流のところでも話をしましたが、人は対象が2つから3つになると途端に混乱しがちです。
男子小学生うん。
なんか難しいと感じてしまうよ・・・
そこで、「対象とする不明な量・モノを2つに絞る」ことが大事です。
これは、上のように図を描くと気づくことです。
女子小学生確かに、
こういう図を描くと分かりやすいかも・・・
こういう図を描かずに、問題文を読み込んだり、にらめっこしていても気づかないことが多いです。
字は走り書きでも雑でも良いので、「状況を整理しながら、考えながら描く」をやってみましょう。
「自分さえ分かれば良い」という描き方で良いでしょう。
記述式の答案に書く際には、多少「採点者に見てもらう」姿勢も大事ですが、書くことを優先しましょう。
何か描いてあれば、採点者は算数・数学のプロなので、
採点者ああ、これは
こういうことを考えているんだな・・・
一目でわかるでしょう。
「採点者に分かりやすい」答案がベストですが、それを「あまり気にしすぎない」姿勢も大事です。
3つの食塩水のてんびん算
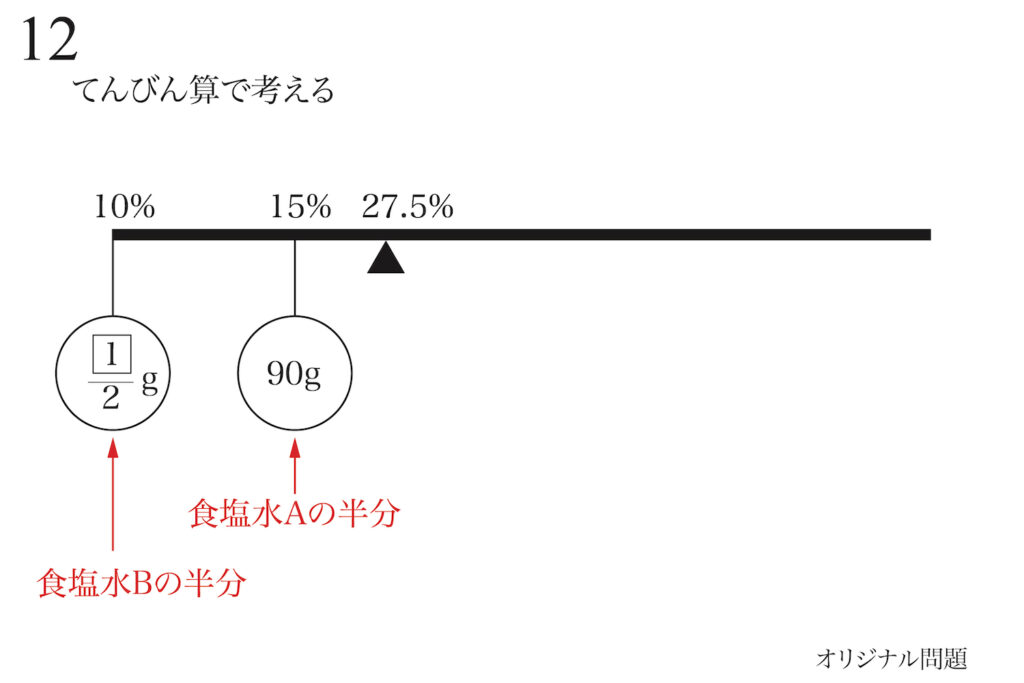
てんびん算で考えましょう。
「混ぜて半分」は「半分にしてから混ぜる」と同じことが分かりました。
そこで、上図のように「食塩水Aの半分」と「食塩水Bの半分」を加えます。
これが最初のプロセスなので、これら「A,Bでてんびん算を描いて解く」でも良いです。
今回は、一気に3つを対象にしましょう。
男子小学生ちょっと
難しそう・・・
女子小学生てんびん算で
3つは大変そう・・・
しっかり理解できれば、難しくないので、やってみましょう。
てんびん算でも他の「〜算」でも、基本原理をしっかり理解していれば、大丈夫です。
考える対象が少し増えても、計算の手間が少し増えるだけです。
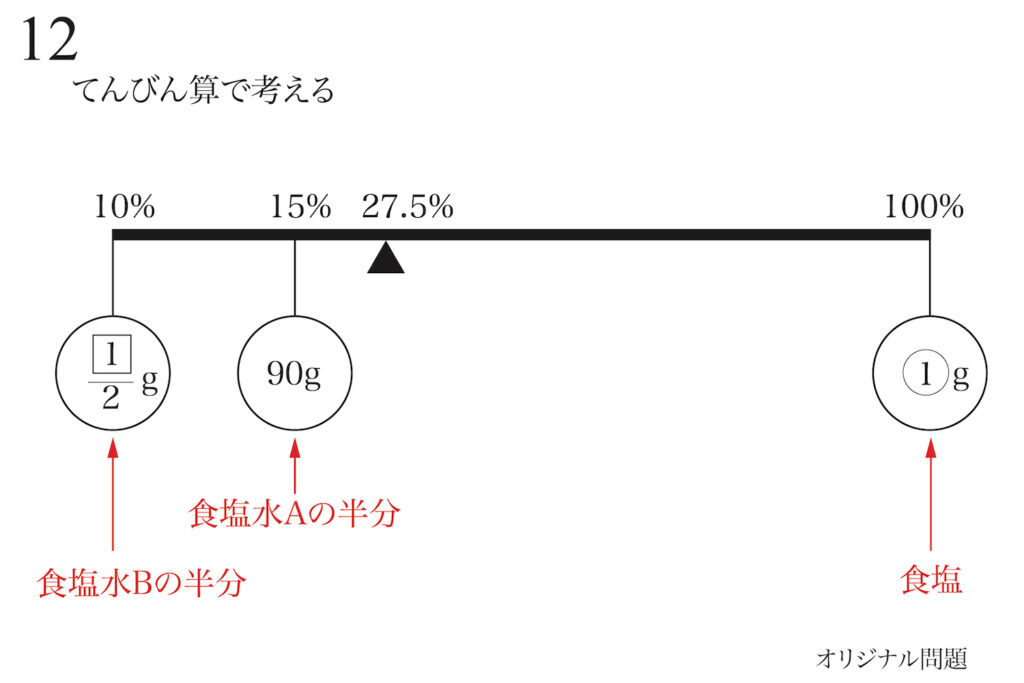
ここで、なかなか「てんびん算」では出てこない「食塩」を描きこみましょう。
食塩は「100%の濃度の食塩水」と考えることができます。
・食塩水の濃度は0%から100%まで連続的に変化する
・塩は「濃度100%の食塩水」で、（真）水は「濃度0%の食塩水」
これで、てんびんが出来ました。
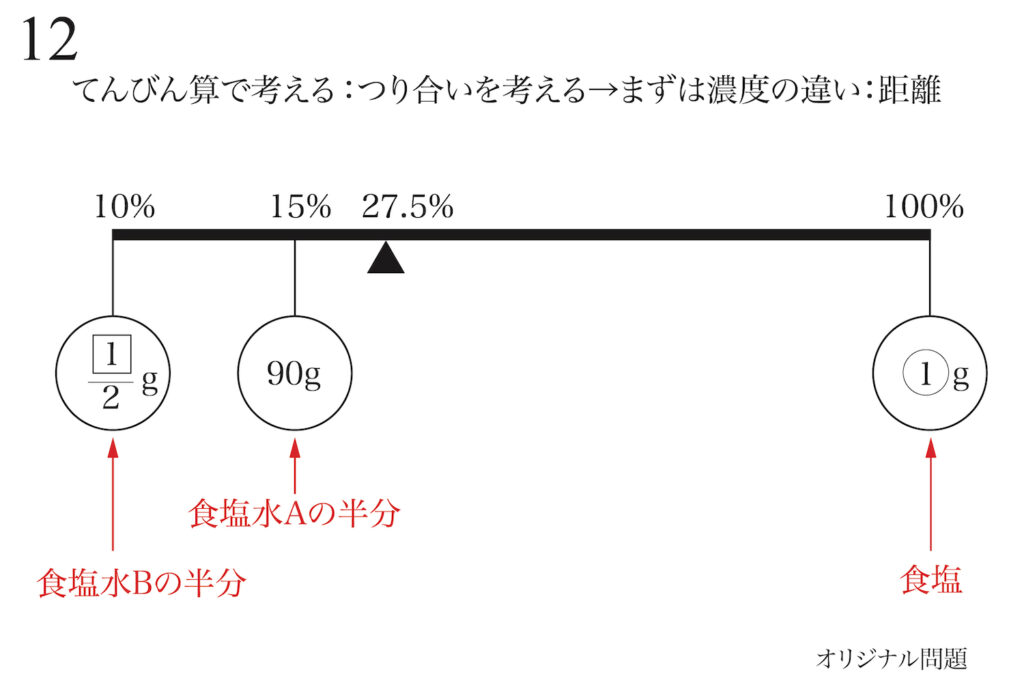
てんびん算は、まずは「つり合いを考える」ので「濃度の違い：食塩同士の距離」を考えます。
ここで、上のような「てんびんを描く」時、「濃度の違いの比例関係」は気にしないようにしましょう。
上の図では、それを表現して「濃度の違い」を適切に表現することも考えました。
その場合、食塩水Aと食塩水Bが「近すぎて、描きにくい」のです。
「濃度の違いの比例関係」は、図の上では「本質的なこと」です。
自宅で大きな紙に描いて勉強するときは、「濃度の違い」を適切に描くと良いでしょう。
試験などで問題を解くときは「考えやすさ」を優先しましょう。
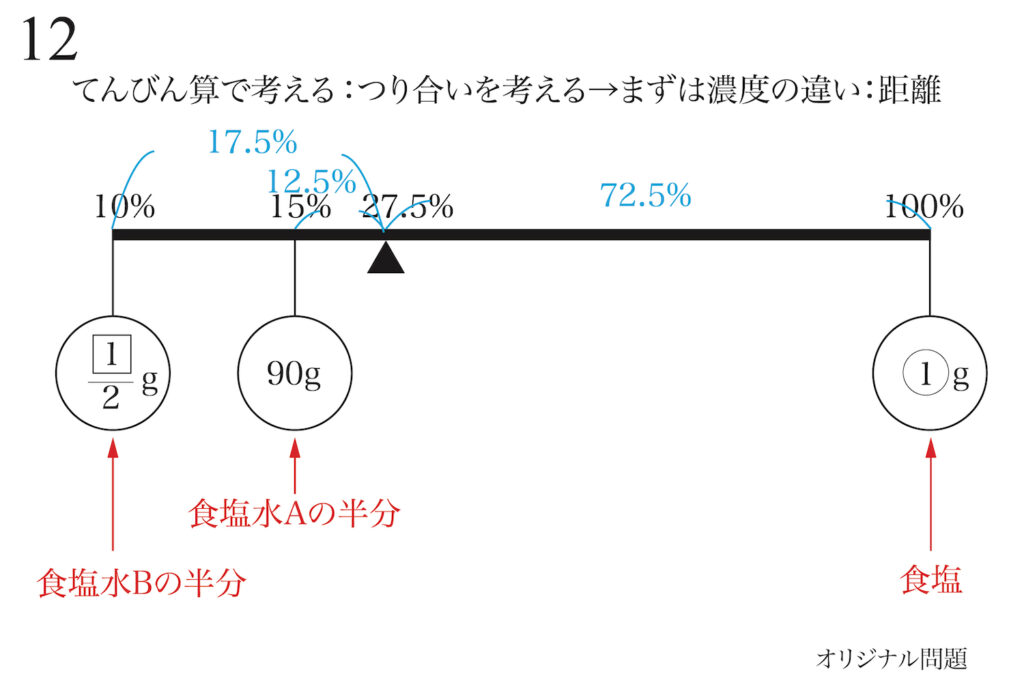
濃度の違いを計算して、てんびんに描きましょう。
この時、上の図のように「17.5%」の%は描かなくても良いです。
大事なことはバランスですから、無次元でも良いのです。
考える対象が3つの時も同じ：2つの時と同じように考える
算数・理科で、てんびん・てこなどで「考える対象が2つ」であることが多いです。
「対象が3つ出てくる」電気・電流ですが「抵抗を求めよ」という問題は少ないです。
男子小学生確かに求めるのは
電流か電圧だね・・・
女子小学生電球の明るさを考えることも
あるけど、電流だね・・・
基本的には「電流を求めよ」で、考える対象は「電圧・電流」であることが多いです。
電気の問題の分かりやすい考え方を、上記リンクでご紹介しています。
上のてんびんのように、対象が3つになると、
女子小学生ちょっと、
これは難しそう・・・
「難しそう」と感じる方も多いかもしれません。
この「難しそう」は、実は「難しく見える」だけです。
「てんびん算」でも電気でも、「考えること（原理・法則）は変わらない」のです。
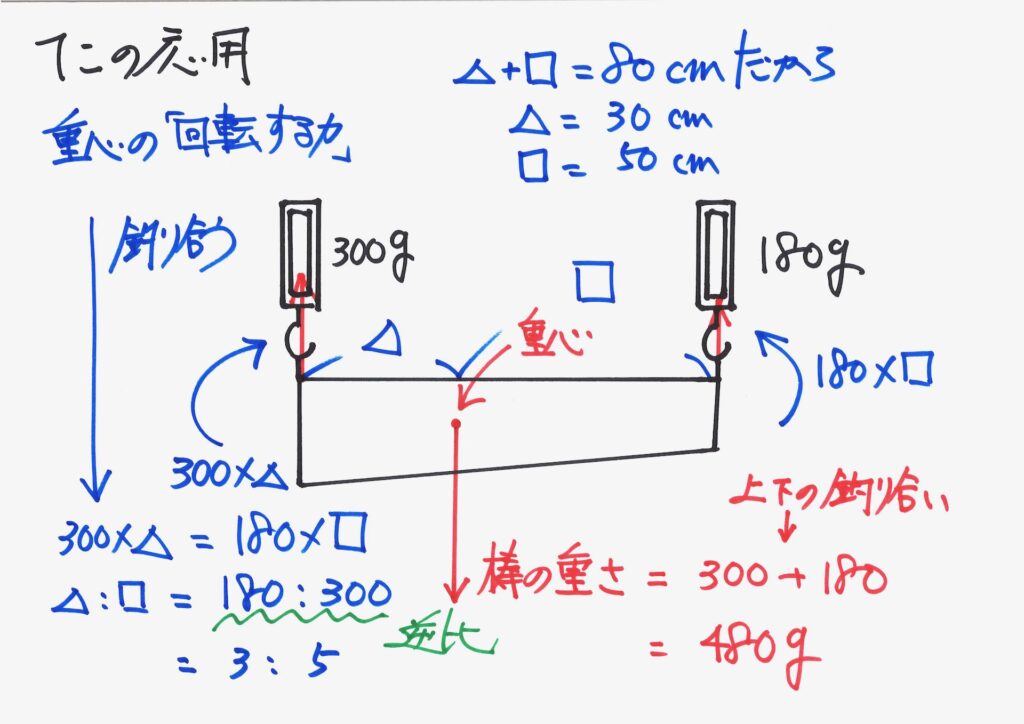
3つの回転する力（モーメント）を計算して、考えてみましょう。
次回は下記リンクです。
