3つの食塩水を「混ぜる」がわかるコツ・ポイント〜3つの重さがある「てんびん」・計算は出来るだけ簡単にする・約数を考えて計算ミスを減らす・大小関係は大まかに考える・問題 12解法〜｜中学受験・算数・3つの食塩水5

前回は「3つの食塩水のてんびん算を「使えない」から「なぜ？」を分かりやすく考えるコツ〜文章題の流れを図解して理解・大事なポイントと量・考える対象を3つから2つへ絞る・考える対象が3つの時も同じ・問題 12解法〜」の話でした。

問題 12

3つの重さがある「てんびん」

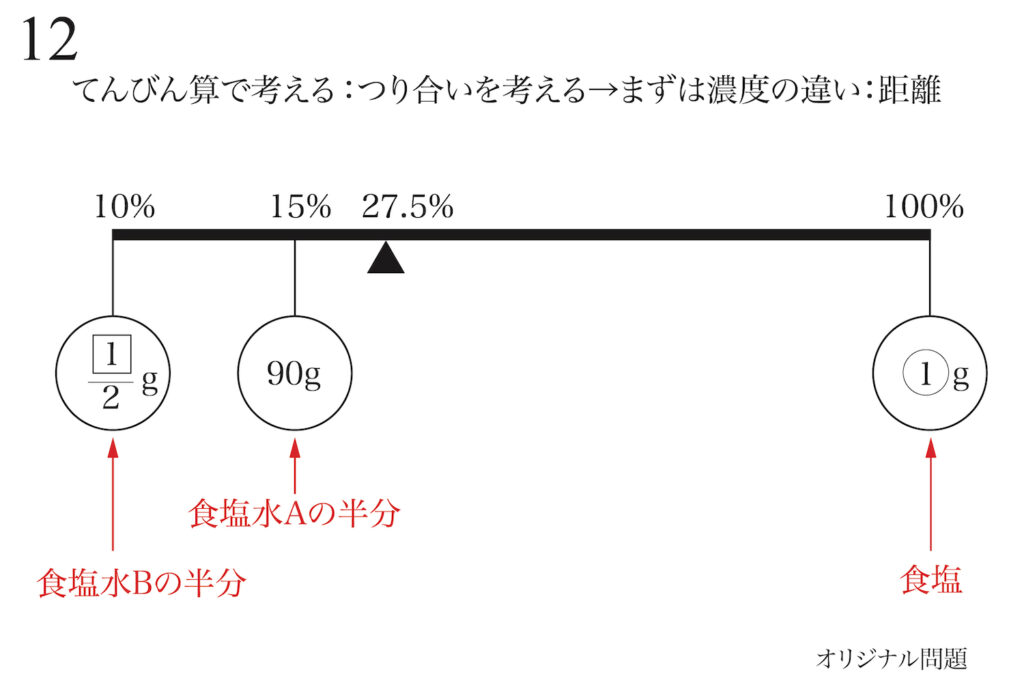
3つの食塩水を混ぜるので、「3つの食塩水をまとめて、てんびん算で考える」をやってみましょう。

てんびんの原理・てんびん算は、「おもり（食塩水）がいくつあっても考えることは同じ」です。

「3つの重さ」が出てきた「てんびん」を、いつも通り考えてみます。

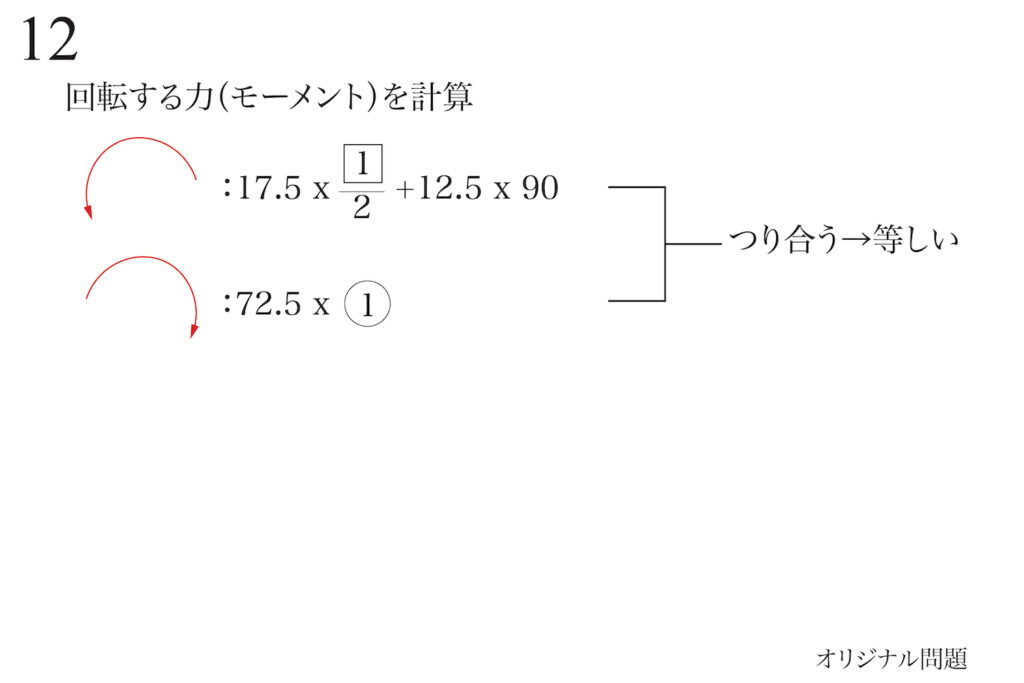
「てんびんのつり合い」を回転する力（モーメント）を計算して考えましょう。

「左回りの回転する力（モーメント）」と「右回りの回転する力（モーメント）」をそれぞれ合算します。

対象が3つになって、難しく見えるかもしれませんが、考えることは同じです。

食塩水が3つより多い、例えば4つ以上の食塩水でも考えることは同じです。

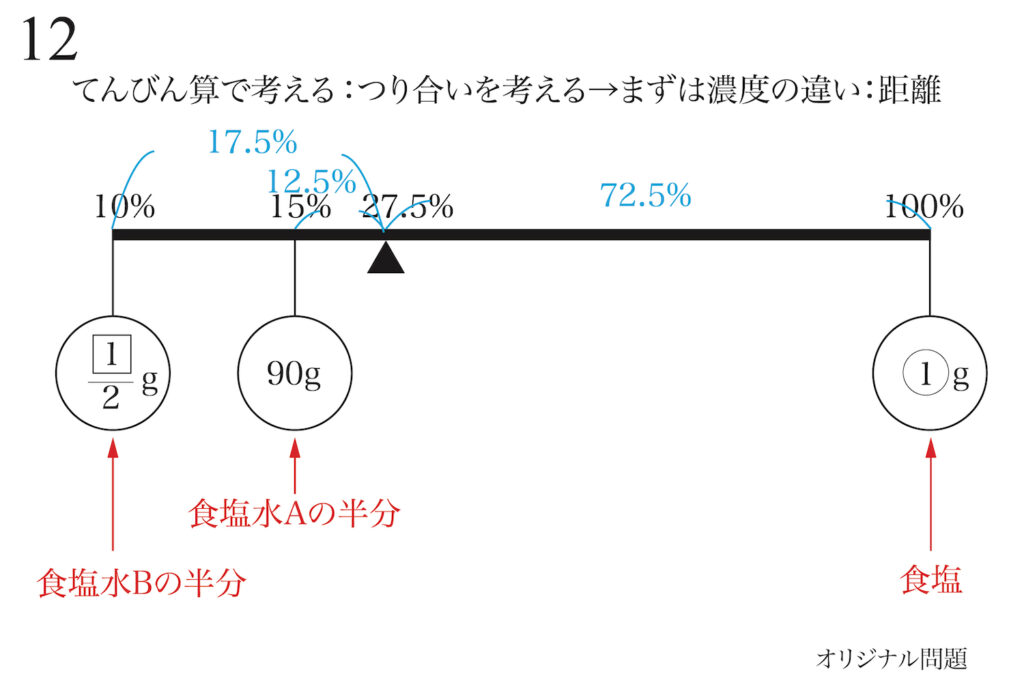
「てんびんがつり合う」ことは、「これらの二つの回転する力（モーメント）が等しい」です。

関係式が立式出来ました。

計算は出来るだけ簡単にする：約数を考えて計算ミスを減らす

ここで、ちょっと待ってください。

ちょっと大変そうな計算式です。

小数点以下があり、事実上3桁の数字を掛け算するのは、少し時間がかかります。

「計算力があること」は、とても良いことです。

こういう時は「計算が簡単にならないかな」と考えましょう。

このように3桁（小数も含めて）の計算で、1/2もあると「計算ミス」の可能性があります。

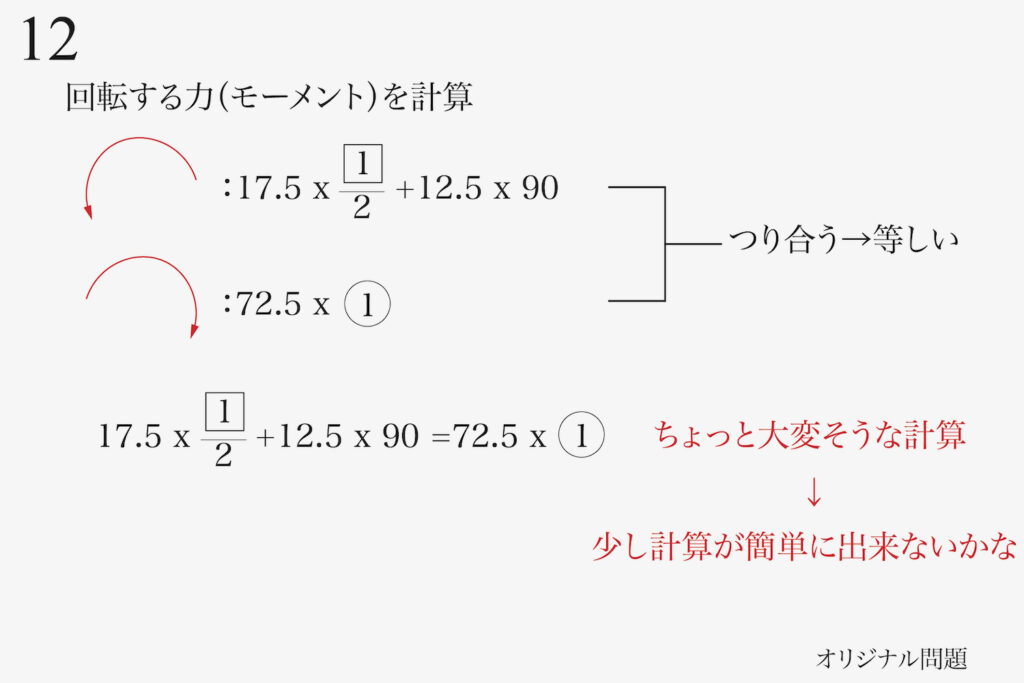
17.5、12.5、72.5を掛けますが、これら「掛ける数」には共通点がありそうです。

少し複雑な計算は「約数を考える」ようにしましょう。

これら3つの数は、全部「2.5の倍数」です。

それぞれが「2.5x〜」なので、

左右の辺で「共通の2.5を割って、消去」出来ます。

このように、ただの計算問題だけではなく、文章題でも「計算の簡略化」を考えるようにしましょう。

算数において、こういう「省力化」と「ミスを防ぐ」姿勢は大事です。

未知数を比較

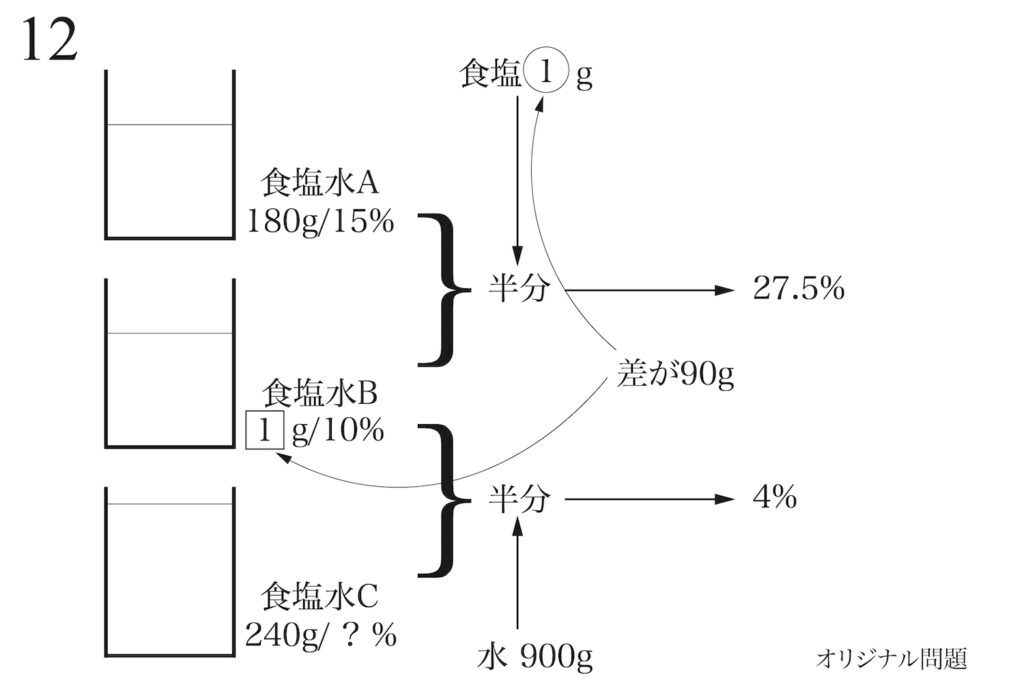
ここで、問題文の「食塩水Bと食塩の差が90g」に注目します。

これで、分からない数（未知数）二つの関係が分かりました。

こういう問題では「〜は〜より90g大きいです」ということが多いです。

この問題は「二つの差が90g」とうところが少し難しいところです。

おそらく「食塩の重さ」の方が小さいです。

ただ、これは「おそらく」なので、しっかり考える必要があります。

以下の部分は少し難しいので、最難関校志望の方向けです。

二つの大小関係を考えるときは、「仮にどうか」を考えます。

「どちらかを考えて（仮定して）おかしい（矛盾する）」ことを考えましょう。

おそらく「食塩の重さ①の方が小さい」ので、「①の方が大きい」と考えます。

そして、「おかしい結論になる」かどうか考えましょう。

大小関係から、上のように「□と◯の大小」が「◯の大小」のみの式になります。

これで、「①がどのくらいか？」が分かりました。

①は「ある数より小さい」で、これを計算してみましょう。

450と51は「3が公約数」ですが、「51=3 x17」で17は素数ですから、計算が小数点以下になります。

これは計算が大変そうです。

大小関係は大まかに考える：「だいたい〜」を考える大事さ

この計算をそのまま実行して、「①<〜」と考えても良いですが、大まかに考えてみましょう。

「〜=〜」という等号関係ならば、計算する必要があります。

「〜<〜」などの大小関係は「大小が分かれば良い」のです。

ここで、「450を割り切れて、51より少し小さい数」を考てみましょう。

すると、50があるので、上のようになります。

これなら、暗算でできるくらい簡単な計算です。

ここで、おかしなことが発生しました。

①は「90より大きく、18より小さい」ので、あり得ないことです。

そこで、「□の方が◯より大きい」ことが分かりました。

算数・理科で、「だいたい〜」と考えることは非常に大事な姿勢です。

上記リンクでは、速さをアバウトに考える話をご紹介しています。

「厳密に分かる」のが望ましいですが、世の中「厳密には絶対に分からない」ことが多いのです。

理科の実験問題でも、「だいたいの大小関係」や「だいたい、こんな感じ」と考えると良いでしょう。

「大体こうかな？」から分かることが多いでしょう。

対して、暗記は「しっかり覚える」必要があります。

その時、「語呂合わせ」でも「丸暗記」でも「暗記できれば良い」です。

「だいたい〜」と考えることも大事です。

社会の暗記に関する話を上記リンクで、ご紹介しています。

社会・歴史の「年号並び替え問題」は、「年号が分かった方が良い」のです。

分からなくても「推測して考える」ようにしましょう。

この「推測」は「だいたい〜」ということです。

「入試に出るすべての年号を暗記する」のは、ほぼ不可能です。

大事な年号は覚える必要がありますが、「細かな知識」が出題される可能性があります。

上記リンクでは、「流れを理解する」歴史の学び方をご紹介しています。

そこで、歴史に限らず暗記も「流れ」を理解しながら直前期頑張ってゆきましょう。

ここまできたら、あとは「しっかり・着実に」計算しましょう。

二つの関係式から、一つの文字を消去して、代入します。

「代入」というと「少し難しい」と感じるかもしれませんが、文字通り「代わりに入れる」のです。

足し算や引き算が中心ですが、しっかり計算してゆきましょう。

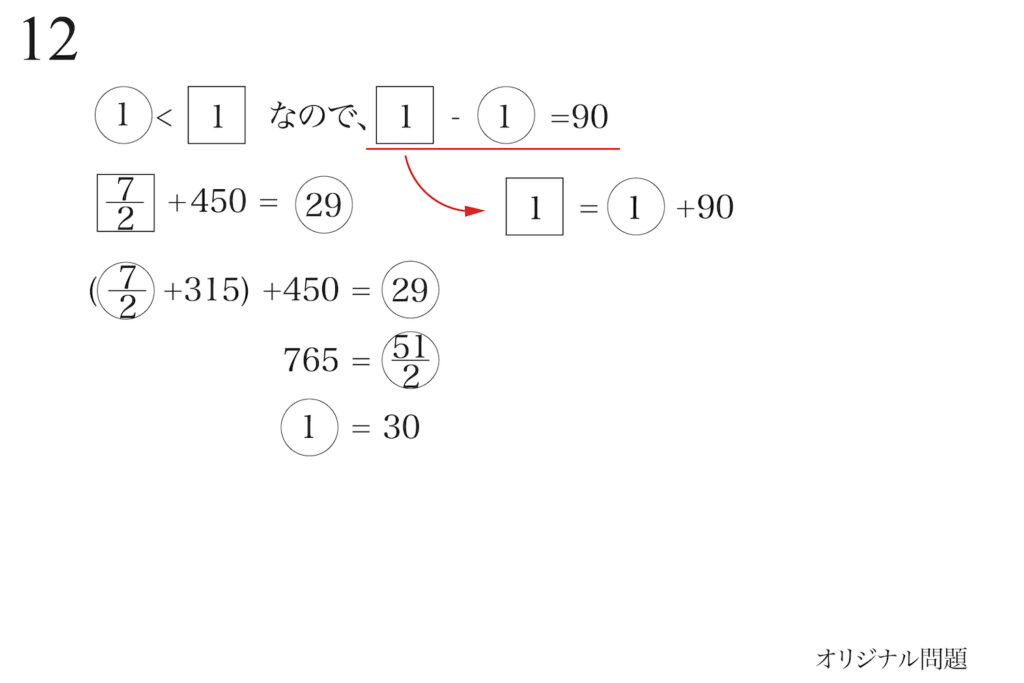
これで①が分かりました。

□も分かりました。

あと一つだけです。

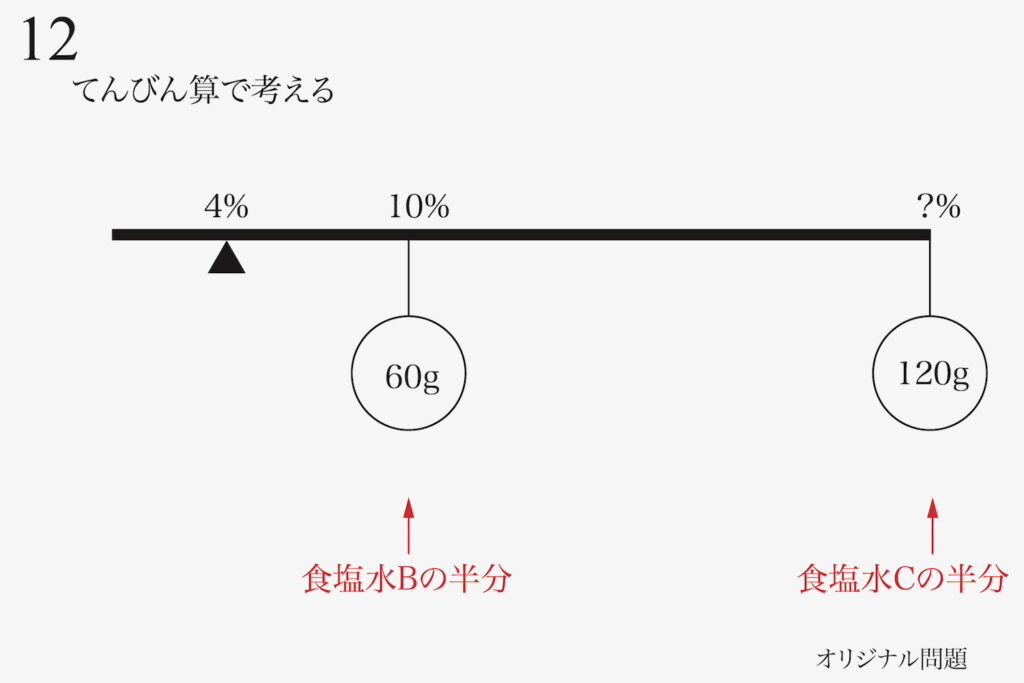
前半と同じように、「食塩水Bの半分」と「食塩水Cの半分」を考えます。

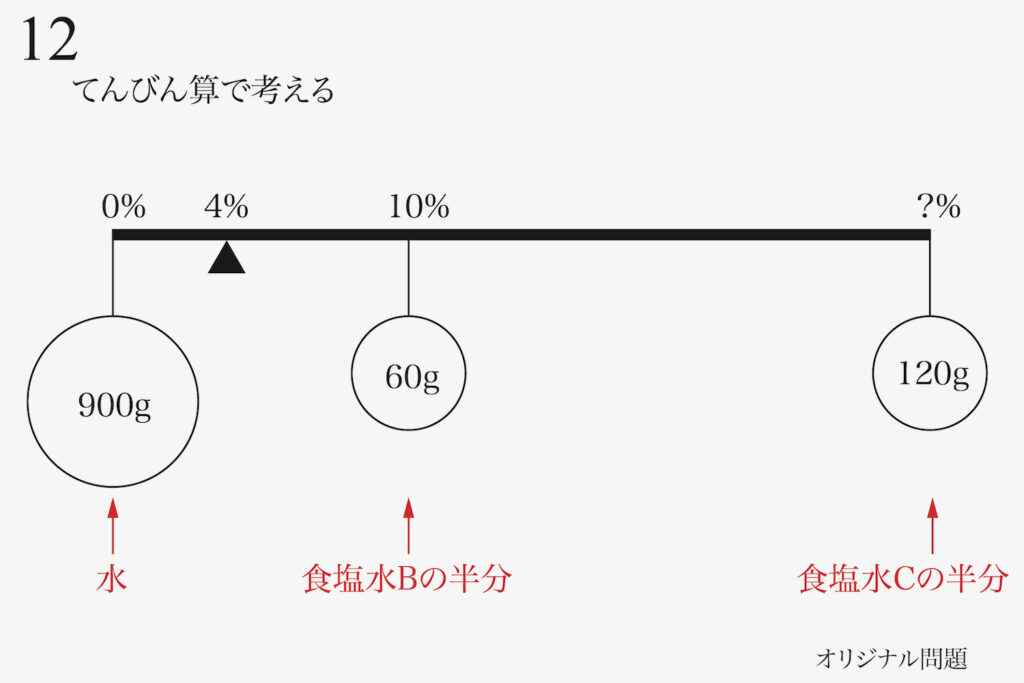
水は「濃度0%の食塩水」ですから、上のようにてんびんが完成します。

濃度の差を考えましょう。

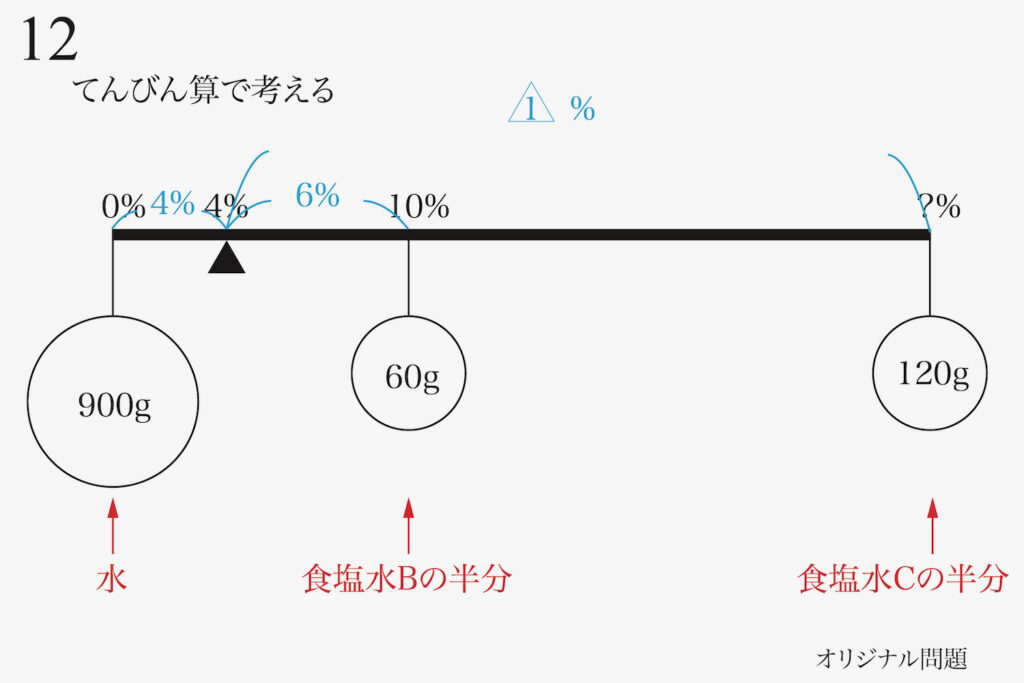
ここで、「食塩水Cの濃度を未知数」としても良いですが、「支点=4%との差を未知数」としましょう。

これは、その方が「計算が楽だから」です。

「食塩水Cの濃度を未知数」として計算しても良いでしょう。

具体的に「回転する力（モーメント）」を計算しましょう。

回転する力（モーメント）のつり合いから、式が求まります。

ここで、少し立ち止まって「簡単に出来ないかな」と考えましょう。

60の倍数が、たくさんあります。

「両辺を60で割る」と、一気に式が簡単になりました。

これで、△が分かったので、食塩水Cの濃度が分かりました。

以上から、

これで、問題12の答えが求まりました。

少し長かったですが、これで長い、複雑な文章題を考える力もつくでしょう。

次回は下記リンクです。