前回は「図図形問題の解き方・ポイント・コツ 1〜色々な補助線・図形全体を描いて学ぶ・センスよりも勘を磨く・図形問題出題が多い理由〜」の話でした。
図形の補助線と「きれいに分割」：辺の比と面積比
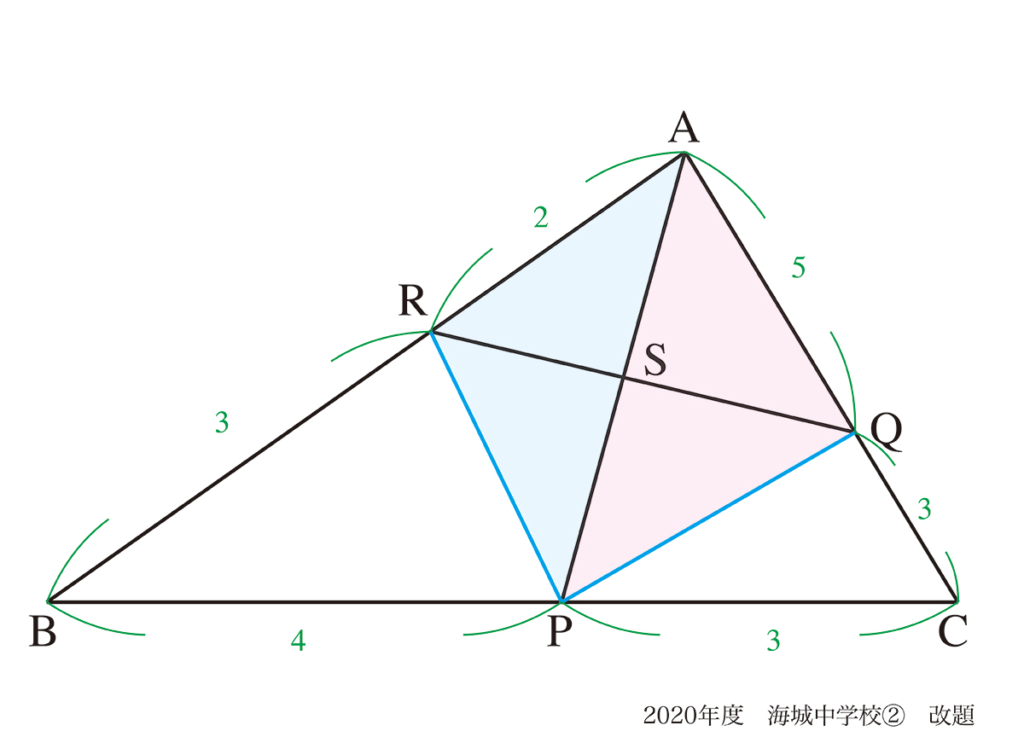
辺の比、または面積比に注目することが多い図形問題。
最も多いのは、相似形を見つけて辺の比を考えて解いてゆく解法です。
最終的に「面積比を求める」問題も多いですが、「面積比を利用する」問題は少数派かもしれません。
その中、算数実践 3でご紹介した解法は「面積比」に着目するとスッキリ解けました。（上記リンク）
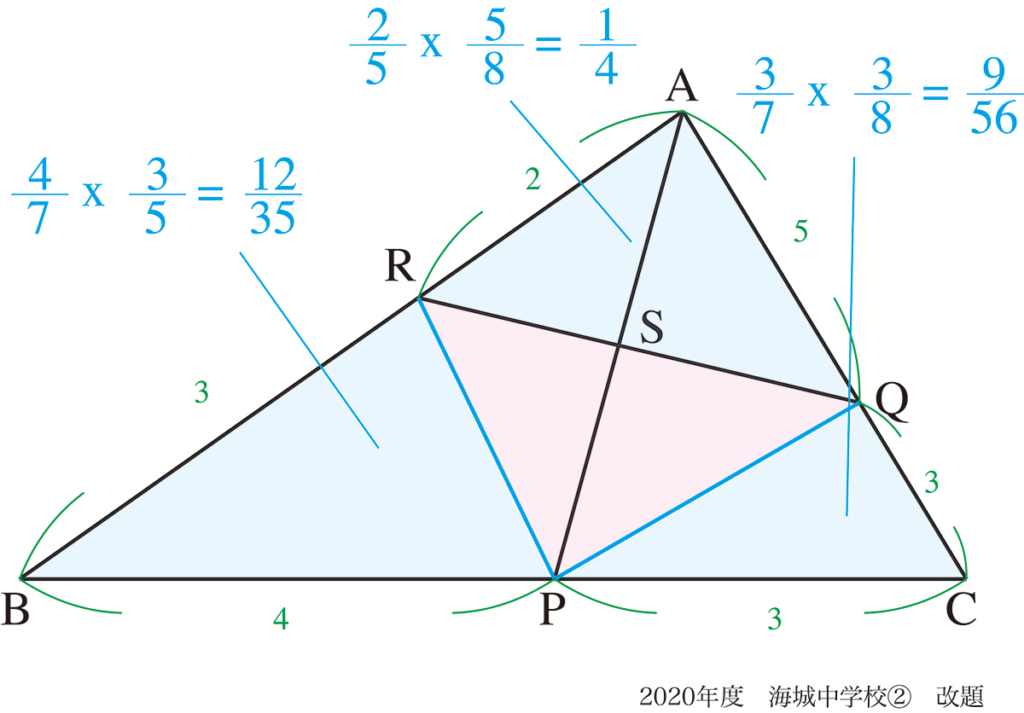
上のように補助線を二本引くと、「いくつかの三角形に分割」出来て、きれいに面積比が分かります。
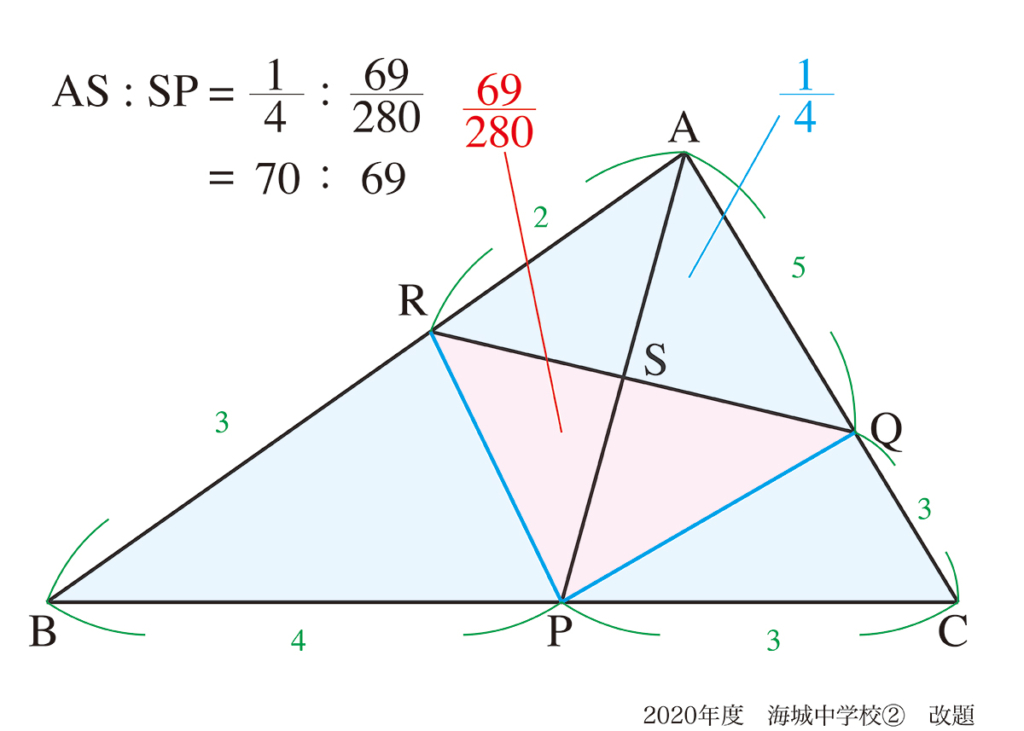
そして、問題の問いの「AS : SP」が求まりました。
「辺の比」から「面積比」や「辺の長さ」を求めることが多い中、この解き方は少し違います。
男子小学生この解き方見たら、
考え方は、分かるよ・・・
男子小学生でもさ、辺の比と面積比の
どちらを考えたら良いのか、どう考えれば良いの？
女子小学生やっぱり、沢山問題解いて、
パターンを理解するのが良いのかな？
この問題では、「図形問題の王道：平行線を引いて、辺の比を考える」が上手くいきませんでした。
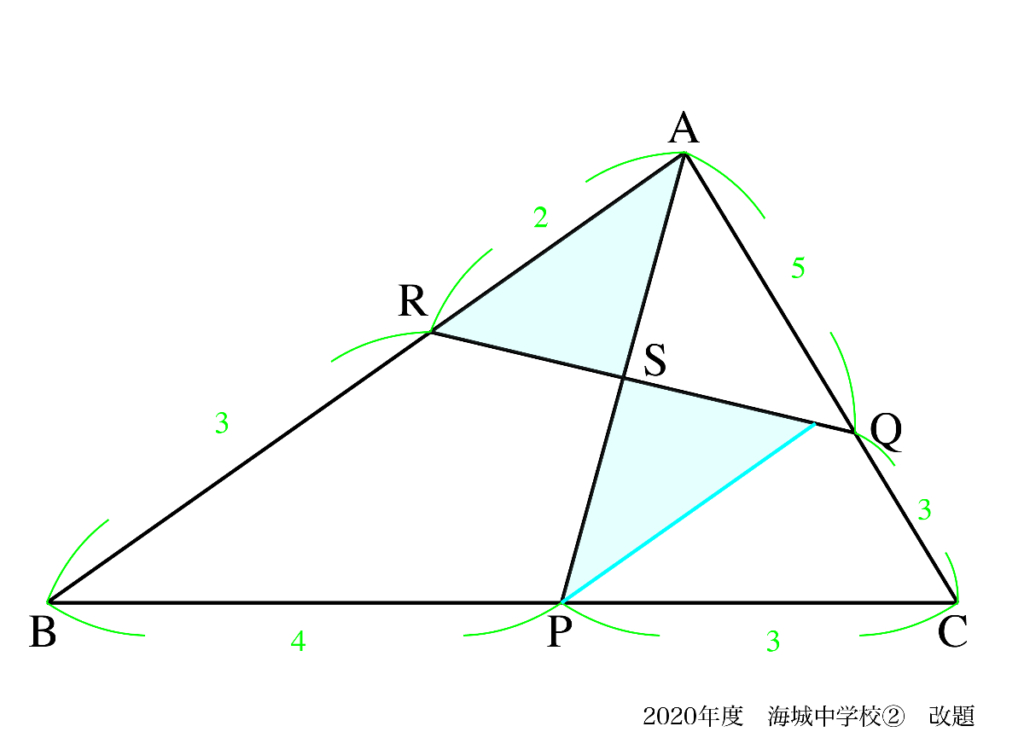
それは、「AS : SP」を求めるために「平行線を引く」と、
女子小学生ここで、「△ASPと△PS〜が相似」
ってやりたいんだけど・・・
女子小学生△PS〜の〜が、
辺SQの途中にあって、分からない・・・
「相似形が見えない」状況になってしまいました。
男子小学生そう・・・
だから、「辺の比でつまづいたら、面積比」なの？
女子小学生どちらかでトライして、
難しそうなら、違う視点で解くの？
そのような考え方もあるかもしれません。
この問題の一つのポイントは、二本の補助線で「図形をきれいに三角形に分割できる」ことでした。
つまり、上の「相似形を考える」時に「辺の途中の分からない」点のような点が登場しないことです。
・図形の中に補助線を1,2本引いたら、三角形・四角形にきれいに分割する
・きれいに分割できたら、それぞれの面積を辺の比から考える
・面積比から、求めたい辺の比を求める
補助線が一本ではなく二本であるのが、少し難しく感じるかもしれません。
ここで、ポイントは「問題の図形が、三角形・四角形にきれいに分割」できることです。
このように、「図形を小さく・きれいに分割」できそうな時は、面積比を考えてみましょう。
男子小学生なるほど・・・
「きれいに分割」がポイントだね。
相似形と辺の比で考えるポイント：図形の外へ飛び出す視点
先ほど、お話ししました通り、「相似形・辺の比」で解こうとすると、手が止まりがちな状況です。
男子小学生じゃ、
相似形・辺の比では解けないんだね。
図形問題では、「解けない補助線・方法」はありますが、「解けない考え方」は、ほぼないです。
「考え方」は、相似形・辺の比・面積比など基本的な考え方です。
男子小学生それでは、
どうやって、この問題を辺の比で考えるの？
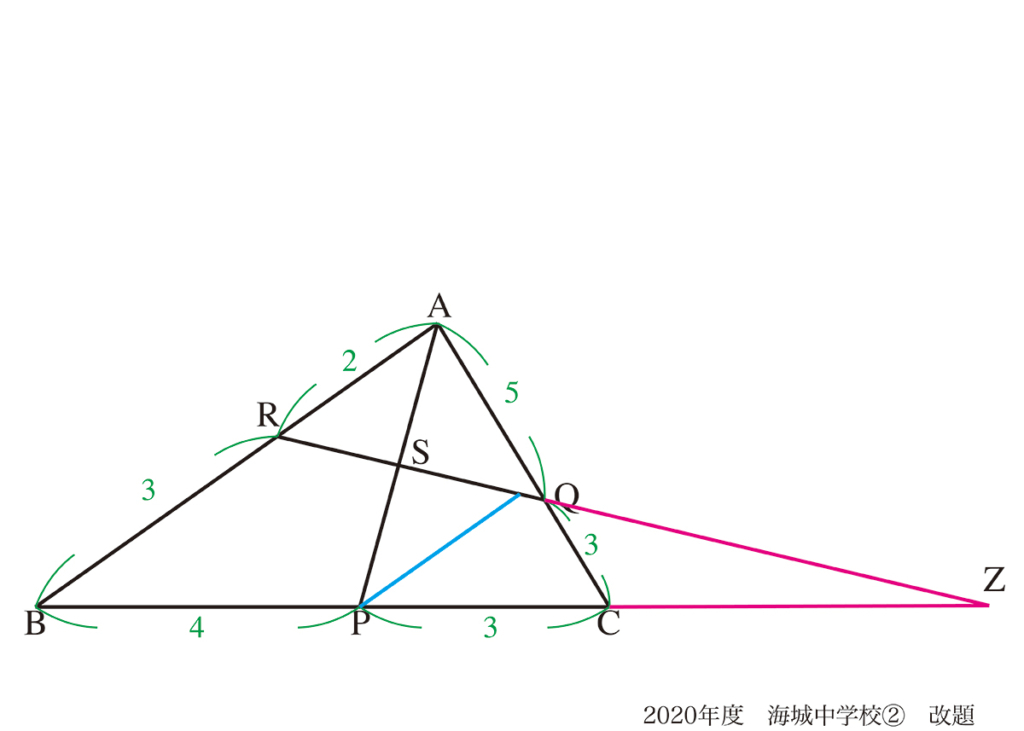
「ABと平行で、Pを通る直線」を引くと、上手くできない雰囲気がありました。
そこで、図形の外に飛び出してみましょう。
女子小学生色々な線・点が増えて、
難しくなるのでは？
「考える対象が増える」と難しくなりそうですが、少しずつ相似形を発見してゆきましょう。
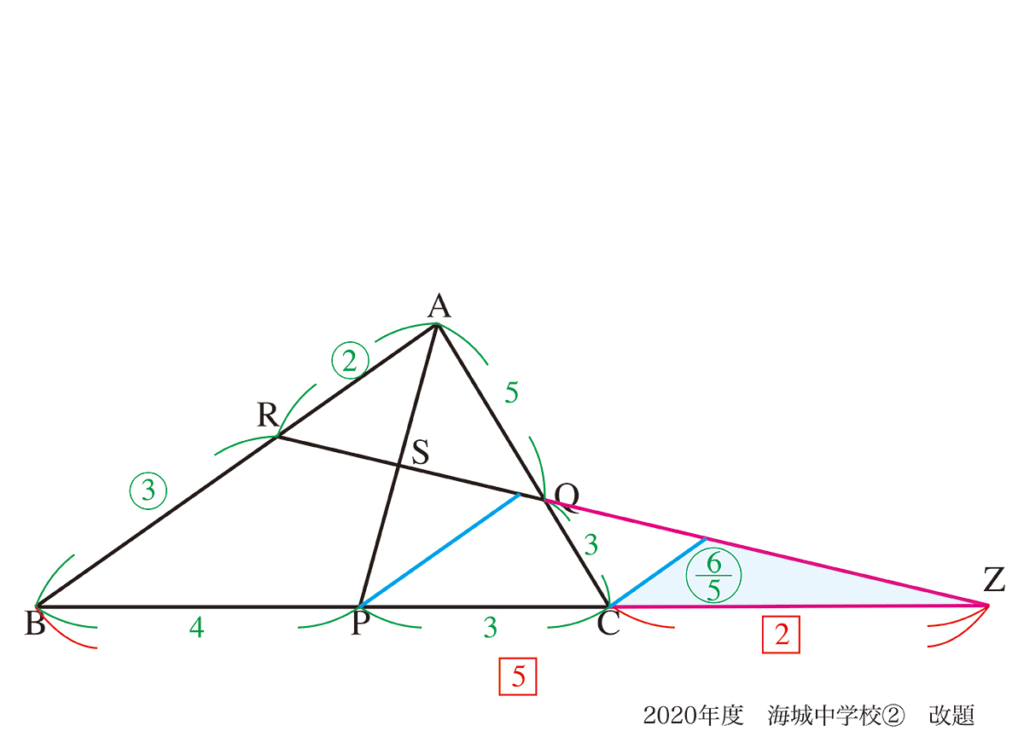
新しい線・点に加えて、相似形もたくさん登場しますが、「順に考えてゆく」ようにします。
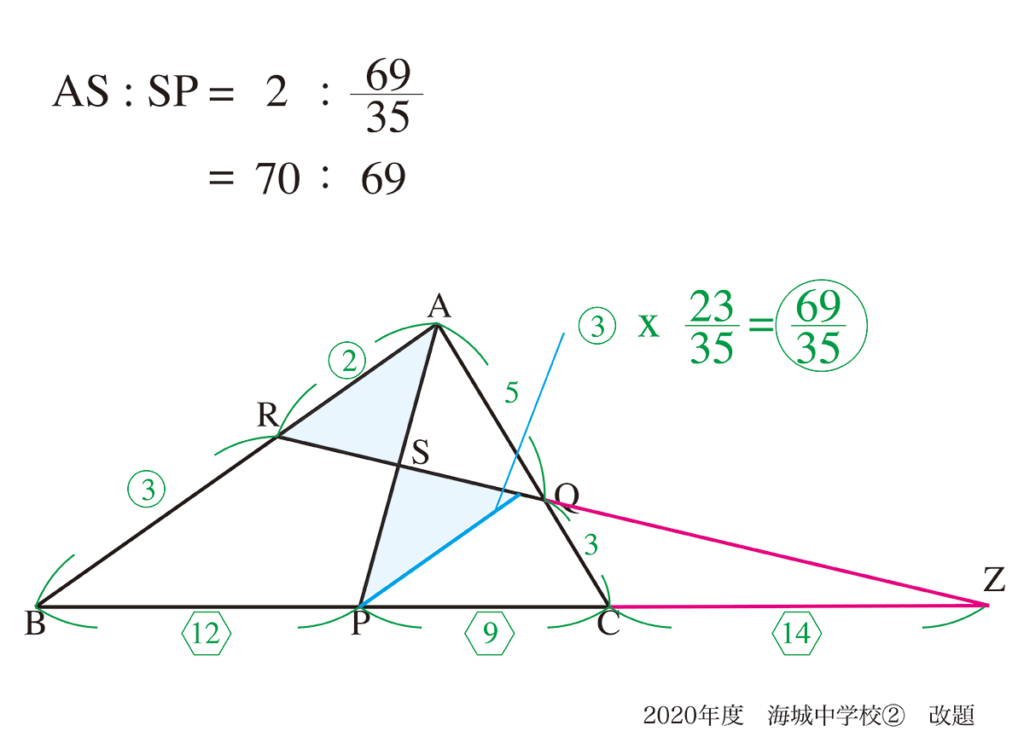
少し、対象とする三角形が多くなり、計算が多いですが、答えにたどり着きました。
ここでは、かなり簡略して表現しているので、詳しくは上記リンクをご覧ください。
男子小学生やっぱり、この問題は
「面積比」の方が簡単だね。
女子小学生「辺の比」でも
解けたけど、ちょっと大変・・・
図形全体を描いてみること=全体像を見ること
二つの解法は、「三角形の面積に着目する」か「相似三角形から辺の比に着目するか」です。
いずれも大事な考え方です。
個人的には、後者の方が応用範囲は広いように思います。
男子小学生そうなの？
でも、「こういう問題は、こう解く」と考えた方が良いのでは？
「こう考える」「こう解く」よりも、意味を考えると学力が上がります。
塾講師こういう問題は、こう解くから、
このパターンを理解して！
このように「ある程度パターン化」して教わる方もいるかもしれません。
算数では「こう考えなければ、解けない」ということは、少ないです。
実際は、「様々な考え方で解ける」のです。
そこで、「こういう問題は、こう」ではなく「こういう考え方もある」と学ぶと良いでしょう。
いずれの解法も「自分で図形全体を描く」ようにしましょう。
図形全体を描いてみると、問題の全容が見えてきます。
男子小学生描かなくても、
見れば分かるけど・・・
「見れば分かる」とは考えず、描いてみましょう。
中学受験・高校受験・大学受験の方は、ぜひこの「図形全体を描く」をやってみましょう。
高校受験の中学生は、図形問題で円が多く登場します。
「円をフリーハンドできれいに描く」のは難しいので、少し歪でも良いので描いてみましょう。
そして、「描くこと」に慣れてゆくようにしましょう。
描いているうちに、慣れてきたりコツがつかめてくるでしょう。
そして、描く時間が短くなり、本質的なことが分かるようになってきます。
「少しでも時間が欲しい」中学受験生〜大学受験生。
こういう遠回りなことをすると、
男子小学生やることが、
たくさんあるよ・・・
男子小学生描くと、
時間がもったいない・・・
「時間がもったいない」と、思うかもしれません。
ぜひ一度やってみましょう。
上記の問題でも、塾や参考書の問題でもいいです。
描いてみると「頭で分かっていたつもり」のことが、より具体化して「見えてくる」感じになります。
この「図形全体を描いてみる」ということが、問題解決のキッカケになることがあります。
図形全体を描いてみることは「全体像を見る・つかむこと」につながります。
解くキッカケがつかめないで、ウンウン悩んで時間が経過してしまうことがあります。
女子小学生確かに、模試とかで
そういう経験たくさんある・・・
「図形を描く手間と時間」があっても、解けた方が良いでしょう。
そして「手を動かして一生懸命考えている痕跡」は、記述式試験において、大いに効果があるでしょう。
図形問題に限らず、文章題でも「描くこと」は効果を発揮します。
上記の解法例では、りんご、みかん、かきを入れる箱は描きませんでした。
ここで、自分で箱を書いてみて、
男子小学生これがりんごで、
これがみかんで・・・
このように、手を動かして状況を理解すると、解きやすくなります。
こういう時の「箱」は、斜め上から見た立体の絵でも、□の平面の絵でも良いです。
男子小学生形は、どちらが
いいの？
立体の絵を描くより、平面の箱を□で表現した方が、早く描けます。
一方で、
女子小学生私は、「箱」は立体的に
描いた方が、わかりやすいけど・・・
「立体的な方が良い」人は、少し時間がかかっても「立体的に描いた箱」にしましょう。
女子小学生どちらでも
いいの？
「どういう考え方が良いか」を考えがちですが、「どう言う考え方が好きか」も大事です。
それもまた「それぞれの方の個性」次第です。
・「どういう考え方が良いか」より「どういう考え方が好きか」
・自分に合った考え方を、しっかりと理解する
この箱の絵を「平面か立体か」でかかる時間の違いは、10秒〜20秒程度でしょう。
一方で、算数で「考えて思考が停滞する」とき、20秒は一瞬で経過します。
「自分の好きな方法」だと、描く効果も高まります。
そして、具体的イメージがハッキリして、思考が進むでしょう。
「こういう時は、こうする！」ばかりではなく、
男子小学生僕は、こうしてみるのが
好きだな・・・
「自分なりの考え方」を大事にして、「好きな方法」を延ばして学力を上げましょう。
手を動かして脳を活性化+イメージ膨らませる
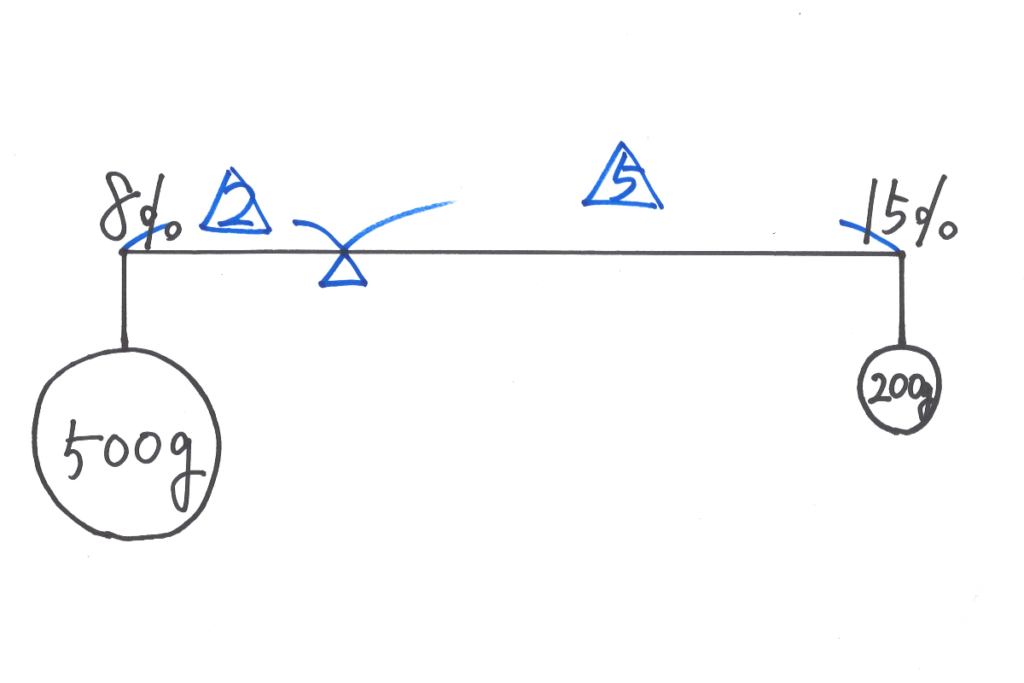
手を動かすことは、脳が活性化します。
悩んでしまって、手が止まってしまうよりも、手を動かして考えてみましょう。
その際は、イメージを膨らませてみるのも良いでしょう。
このてんびんの図は、筆者が手描きで描きましたが、少し誇張しています。。
500gと200gの食塩水をおもりに見立てる時、おもりの直径が食塩水の量に比例するように描きました。
実際は量＝面積と考えられるので、直径が500/200=2.5倍で描くと面積が2.5×2.5=6.25倍になります。
厳密には左側のおもりのサイズ（直径）は右のおもりのサイズ（直径）の「2.5の平方根倍」になります。
量の違いはイメージできた方が良いので、大きい方を大きめに書いてみました。
慣れてくると「同じ大きさ」で、おもりを描くと思います。
このように量や大きさが大きいものを実際に大きく描いてみると、イメージが膨らみます。
算数と理科が横断的に繋がって、理解力が深まるでしょう。
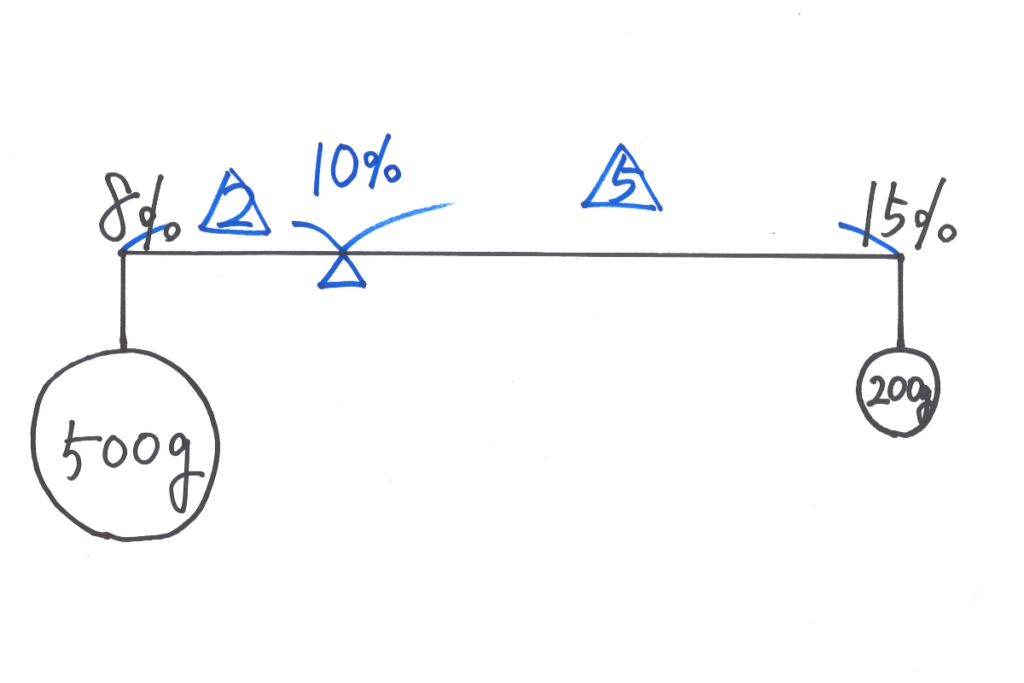
てんびんの釣り合い位置は、掛け算（モーメント）で考えます。
感覚的にも大体下記のような感じだと分かります。
図形でも文章題でも、自分がイメージ膨らむようにどんどん描いてみましょう。
そして、解法のキッカケを、自分の手でどんどんつくってゆくようにしましょう。
次回は下記リンクです。
