前回は「図形問題を「苦手」「嫌い」にならない姿勢〜三角形と相似形の解き方・面積比・辺の比・問題 2〜」の話でした。
問題2（再掲載）
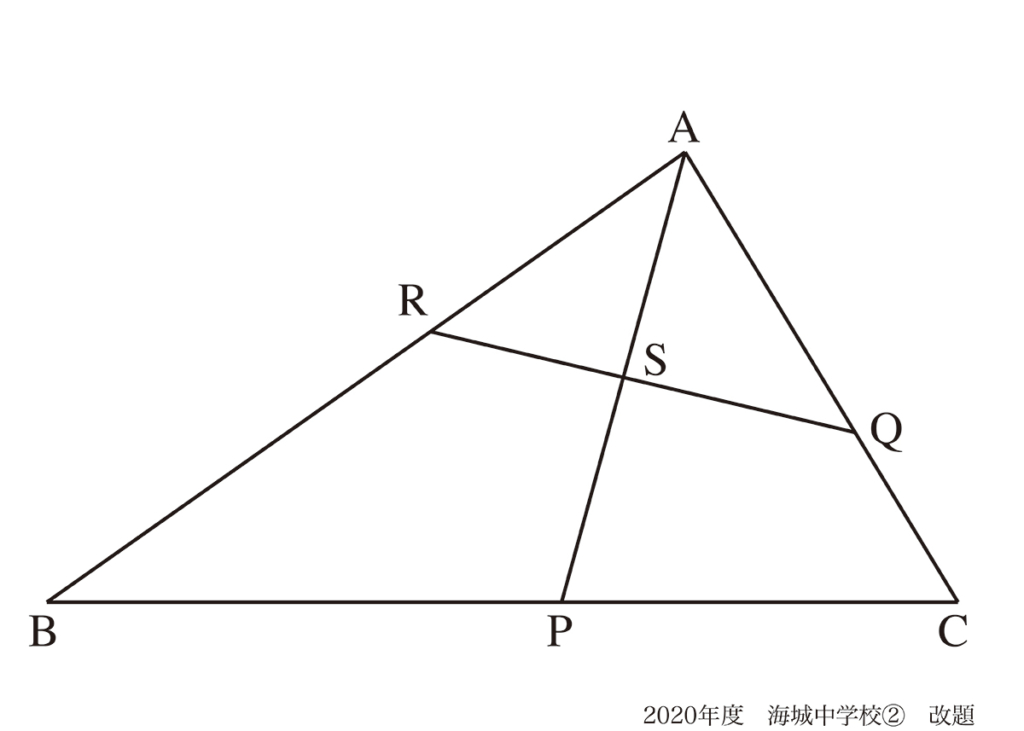
三角形の一辺に平行な補助線：補助線の役割(2)解法A
今回は、三角形の相似比から考えます。
辺ABに平行で、点Pを通る補助線を引いて見ましょう。
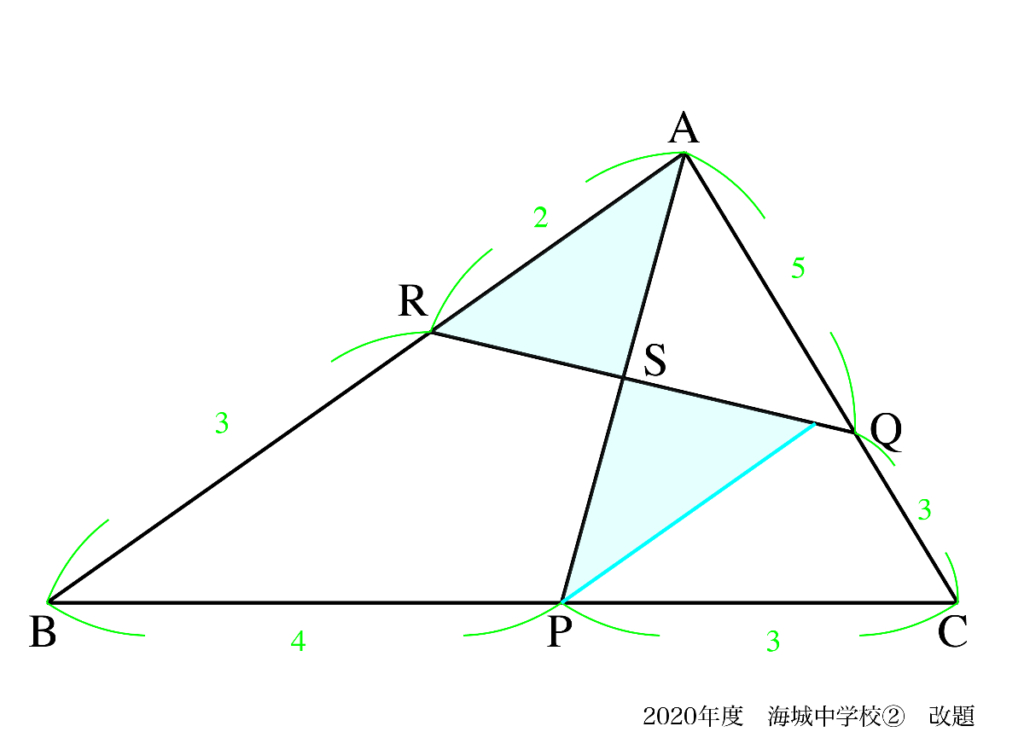
男子小学生上の図で水色の二つの図形は
相似形だけど・・・
男子小学生これでは、
進まない気がする・・・
なかなか「解くキッカケになる相似三角形」が見えません。
男子小学生この補助線では
解けないのかな・・・
この問題を「辺の比」で解こうとすると、前回の「面積比」で解くよりも「やや難しい」かもしれません。
前回、「面積比」で考えた時と今回「辺の比」で考えている時、補助線の大きな違いは何でしょう。
女子小学生補助線の違いを
考えるの？
今回の「ABに平行で、Pを通る補助線」は、なぜ「解けない感じ」なのでしょうか。
女子小学生それはね・・・
あ、そうだ！
女子小学生この補助線が
辺SQの途中でぶつかっているからだ！
男子小学生そう！
この補助線が、たとえばPQだったら解けそう！
問題に登場していない「新しい点」が出てきたことが、「この補助線」の問題点です。
そのため、「相似形を解くための比が分からない」状況です。
男子小学生そういうことだね。
では、この補助線では解けないの？
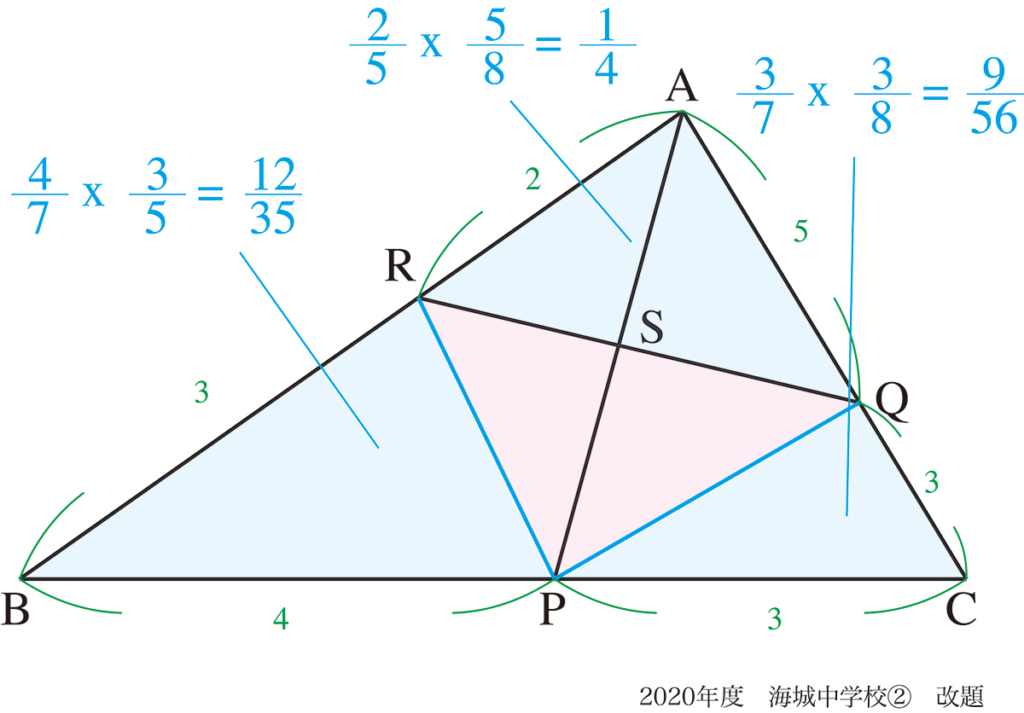
実は、この補助線でも解けるので考えて見ましょう。
図形の世界を広げる発想：視野を広げる
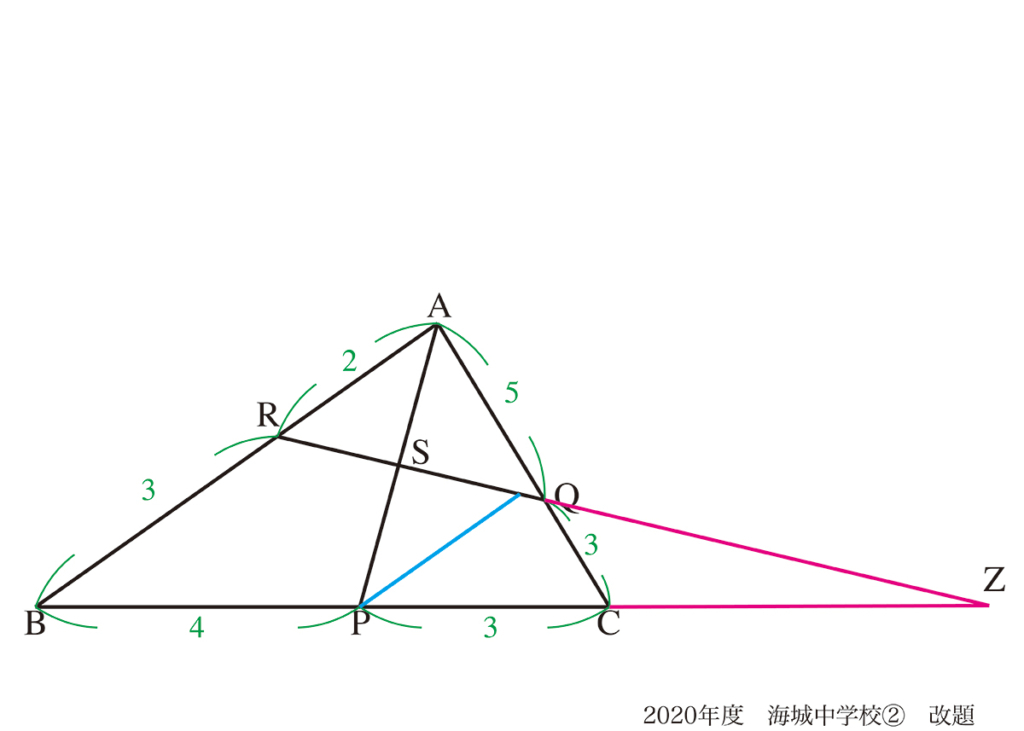
少し視野を広げて、図形の外に飛び出して、新しい三角形を作ってみましょう。
図形問題は「与えられた図形の中だけ」で考える必要はありません。
男子小学生これは、解くのが
難しくなるんじゃない？
女子小学生三角形ABCの外に出ると、
図形が難しくなった気がする・・・
「難しい」ように見えるかもしれませんが、一つ一つ「相似形・辺の比」を考えて見ましょう。
RQとBCの延長線の交点をZとします。
これによって、△BRZが現れ、相似三角形が見えてきました。
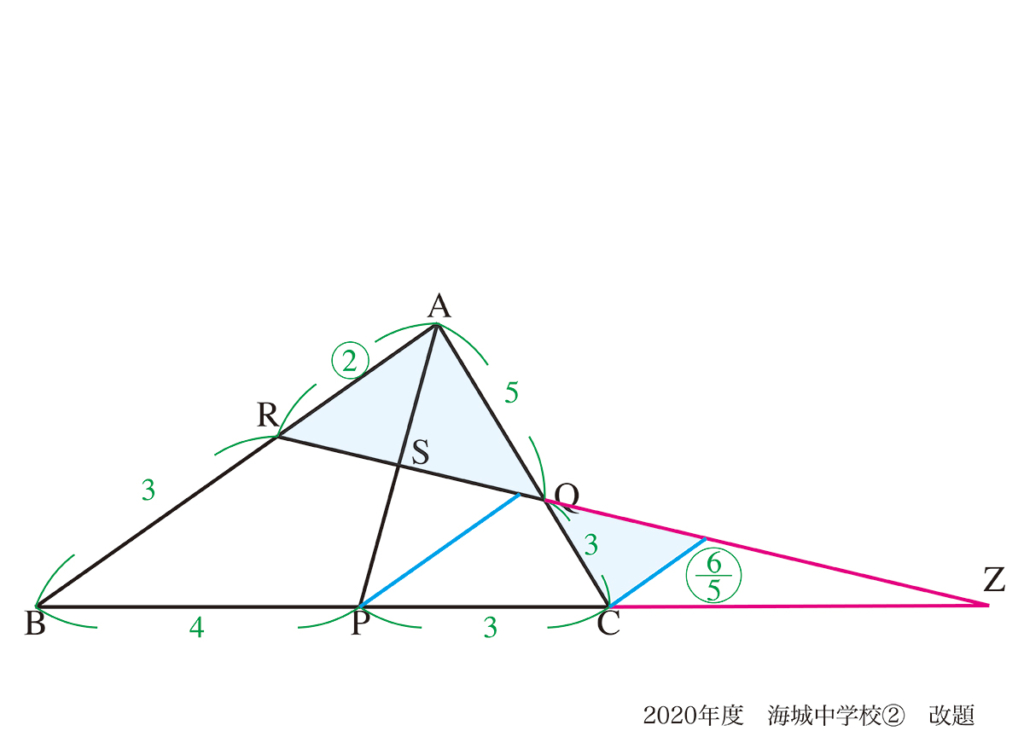
まずは、△BRZにおいて、BP : PC : CZの比を考えましょう。
上図でCからABに平行な直線を引き、水色の相似三角形を考えて、辺の比が求まります。
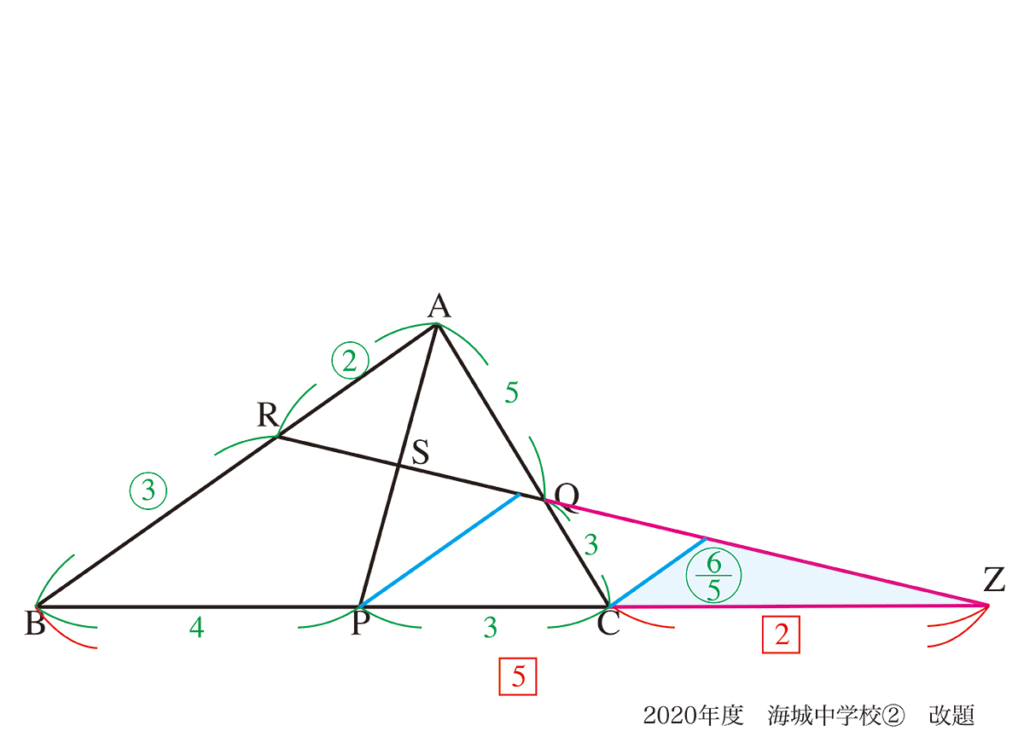
そして、△BRZと上図水色の三角形が相似なので、BZ : CZ =3 : 6/5 = 5 : 2となります。
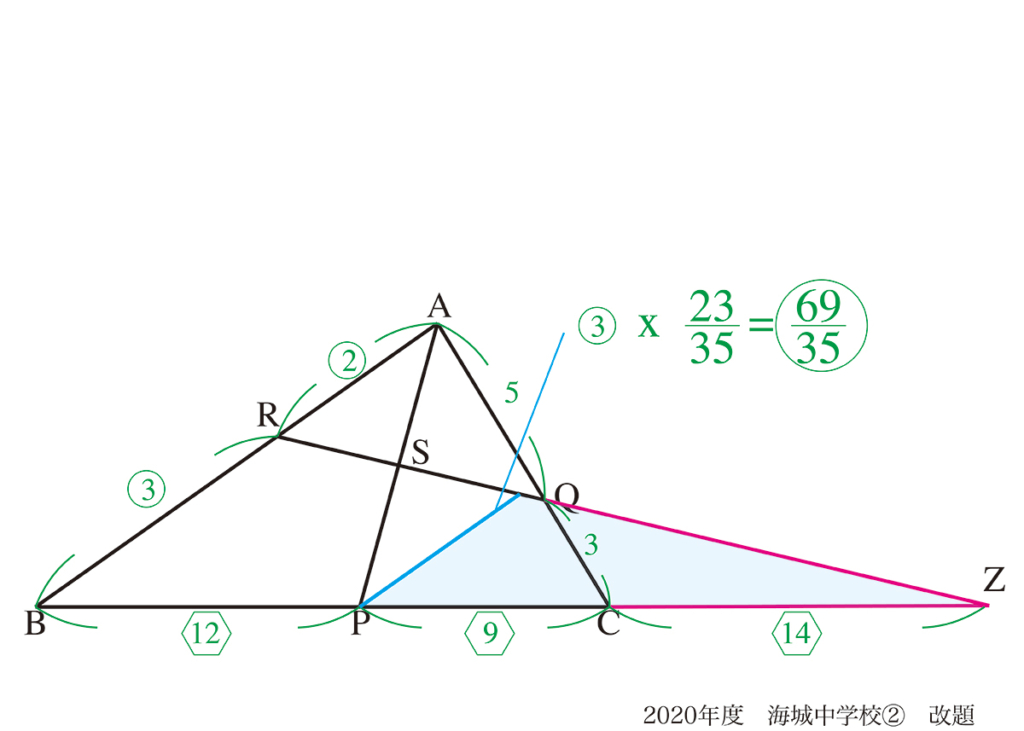
辺BZにおいて比を整理して、BP : PC : CZ= 12 : 9 : 14と求まります。
最後に△BRZと上図水色の三角形が相似ですので、辺の比が求まります。
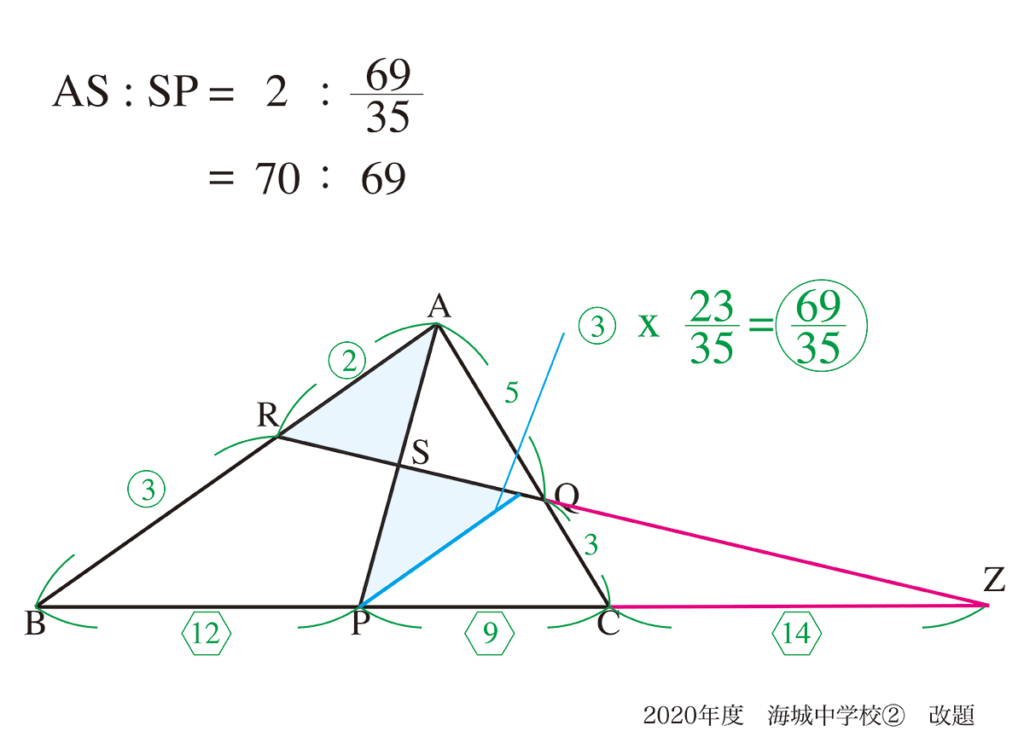
すると、AS : SP= 70:69と求まります。
多角的視点：複数の解法を習得して様々な角度から考える姿勢
面積比と辺の比の両方の考え方を比較してみましょう。
(2)に関しては解法Bの方が考え方は易しいですが、計算が大変です。
解法Aは丁寧な説明を心がけたため、少し図が多くなりました。
慣れれば、相似三角形を自分でどんどん作れるので、計算は比較的簡単です。
男子小学生慣れるようになるには、
どうしたら良いの？
慣れるには、「自分でどんどんやってみる」のが一番良いです。
・図形全体を描いて、しっかり考える
・自分で補助線を引いてみる
解法Aの方が短い時間で解答に至り、「計算ミスを防ぐ」面でも効果的と思います。
異なる視点で説いてみましたが、解法Aで大事なことは「図形の外に飛び出す」ことです。
問題の世界は、出題者の決めた中で完結しなくても良いのです。
特に図形問題は、「自分で世界を広げて考えてみる」をやってみましょう。
次回は下記リンクです。
