前回は「「出来ない・成績が上がらない」から「出来る・成績が上がる」勉強法〜「採点者に自分の考えを伝えること」が大事な記述問題・考え方と解法の流れを書く・式の羅列に接続詞を追加〜」の話でした。
「伸びない・解けない」から「伸びる・出来る」勉強法：条件を明確化
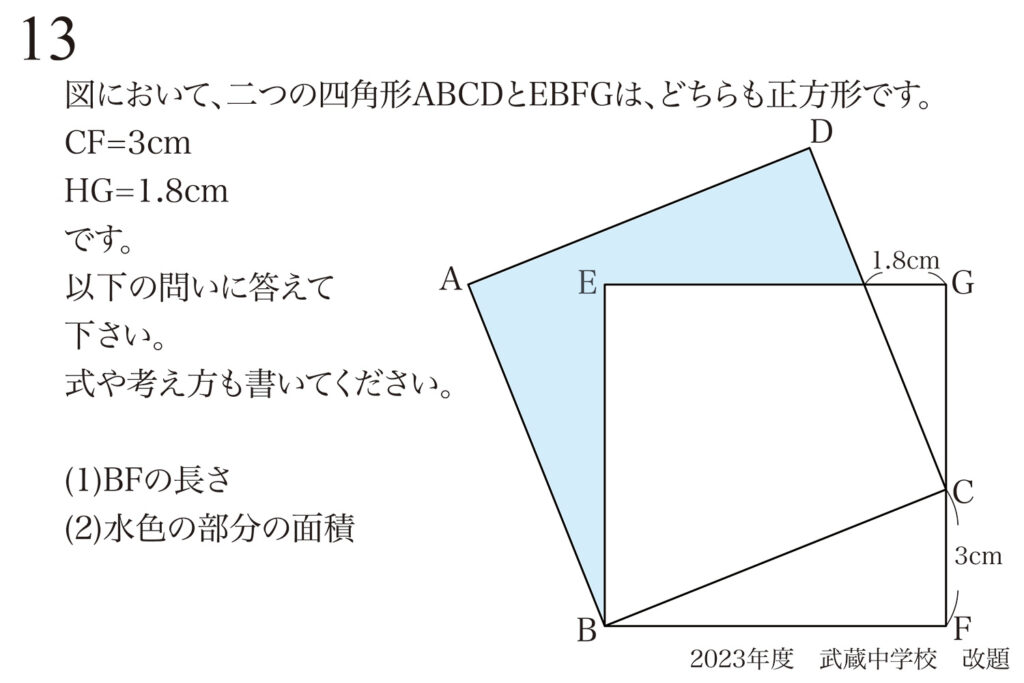
二つの正方形が登場する上のような問題を考えました。
図形問題の条件では、正方形や正三角形が頻繁に登場します。
男子小学生確かに、図形の一部が
正方形の問題は多いね・・・
女子小学生あと直角三角形も
比較的見かけるけど・・・
正方形や正三角形は「非常にわかりやすい」図形です。
その基本的性質は「分かっている」方が多いので「正方形」があったら、
男子小学生この正方形は
分かるから、問題の〜を考えて・・・
「正方形は分かるから、大丈夫」と考える方がいるかもしれません。
方眼紙やグラフ用紙などで「馴染み深い」正方形は、「わかりやすい図形」です。
わかりやすく、非常に基本的な図形である正方形・正三角形には「問題を解く鍵」が詰まっています。
・非常に特徴的な図形であり、全ての基本的性質を理解
・正方形・正三角形には「基本的性質=問題を解く鍵」が沢山ある
正方形の基本的性質を復習しましょう。
・全ての辺が同じ長さ
・全ての角が同じで直角
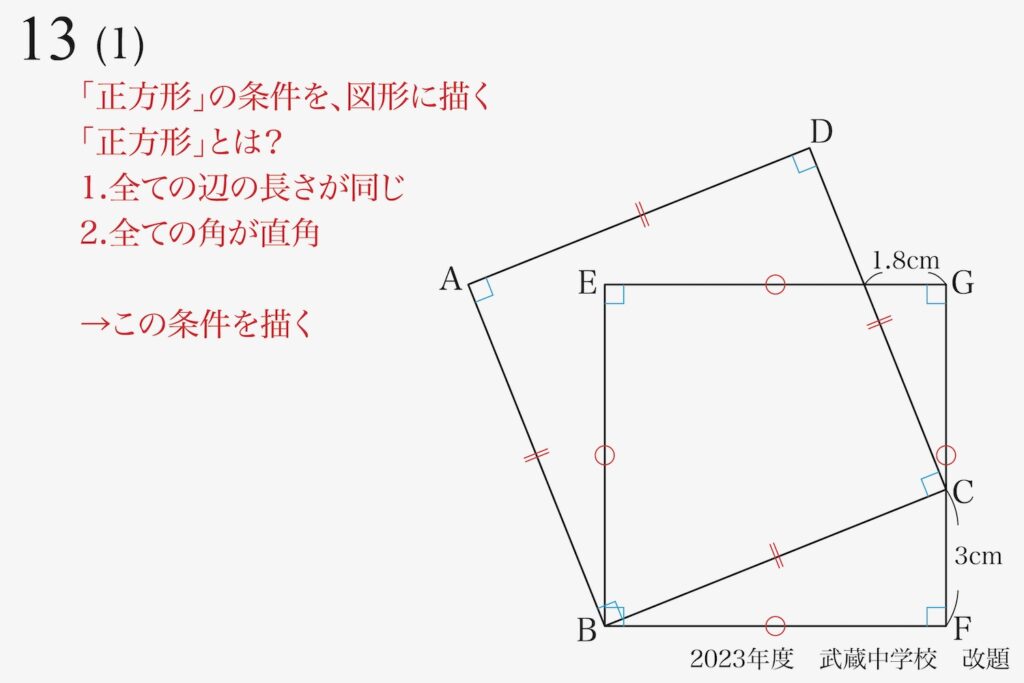
まずは、これらの「等しい辺と直角」を図形に描きこみましょう。
これだけでも「問題を解く鍵」が見えてくる可能性が一気に高まります。
男子小学生確かに、こうして
描きこんだ方が分かる気がする！
女子小学生「全部わかっていること」なのに、
描いた方がとっても分かるね！
いくつか補助線を引いてみる姿勢
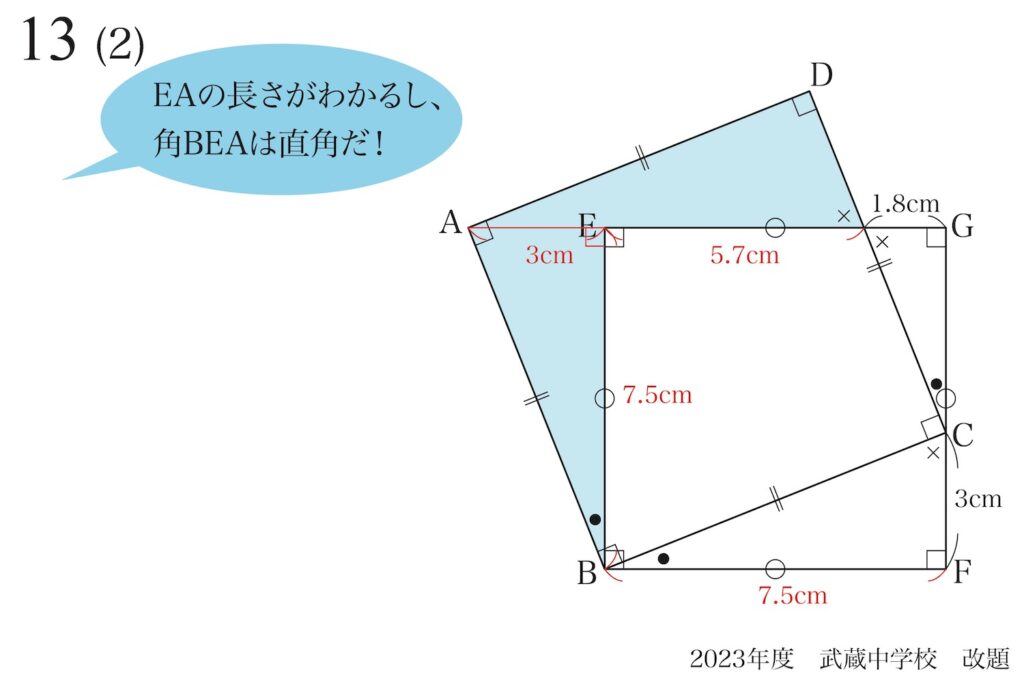
図形問題では、「どのように補助線を引くのが効果的か」などを考えてみましょう。
問題集などでは、補助線が突然引かれることが多いです。
塾講師この補助線が
良いです。
塾講師この補助線を
思いつけるようになりましょう。
補助線には「良い補助線」と「良くない補助線」があります。
「良い補助線」とは「見通しが良い補助線」です。
「良くない補助線」とは「見通しが良くない、解けない補助線」です。
このような図形問題が解けない時、解答を読んで、
男子小学生ああ、ここに
補助線引けば良かったんだ・・・
男子小学生ふ〜ん・・・
こう引いて、ああそうか・・・
「そうなんだ」と感じることが多いです。
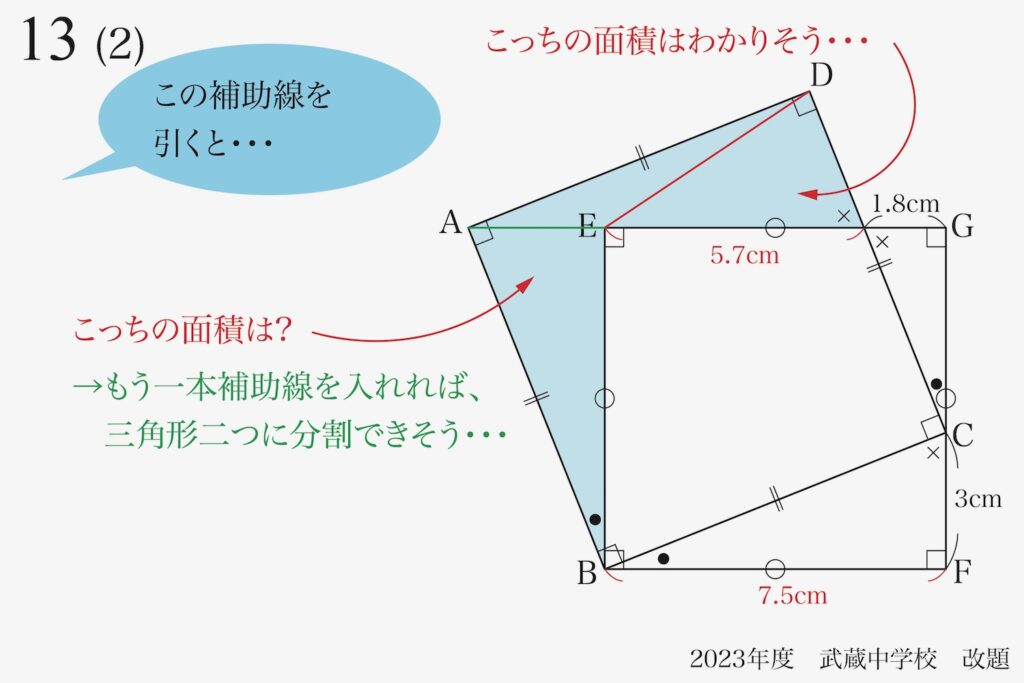
ここで、「自分が考えた補助線」や「異なる補助線」と「解答の補助線」を比較してみましょう。
女子小学生この補助線では、
解けなそう・・・
比較してみると、「解けなそう」であることが分かります。
そういう「見通しの良くない」補助線を実際に体験することも大事でしょう。
女子小学生なぜ、この補助線が
見通しが良くなるんだろう・・・
この「なぜ？」の視点も大事です。
二つの正方形の問題を解くコツを、上記リンクでご紹介しています。
・「良い補助線=見通しが良い補助線」と「良くない補助線=見通しが良くない補助線」を比較
・比較することから「補助線のコツ・勘」が磨かれる
将来につながる「なぜ？」「どうして？」：試験対策と本質的学力
「なぜ？」「どうして？」という視点は、算数・理科では非常に大事です。
「なぜ？」を大事にしたエジソンの話を、上記リンクでご紹介しています。
中学受験の算数は、非常に難しい問題も多いです。
そうした難問が「解けること」は、非常に高い学力・解決能力を持っていることになります。
ところが、その「解決能力」が「その後につながる学力か」は別問題です。
水泳の泳ぎ方と学び方に関する話を、上記リンクでご紹介しています。
難しい問題が多く、時間内に解くべき問題数も多い難関校〜最難関校の中学入試。
問題単体を見ても「難しい」と感じる問題が多数あります。
さらに、50~60分で対処しなければならない問題数もかなりのものです。
「70%程度をしっかり解ければ、合格ライン」であっても、その「70%を確保」するのは大変です。
中学入試の全体、主に算数の難化傾向があります。
その理由は「長年にわたって様々な問題が蓄積されてきたこと」が大きな理由です。
出題者は算数・数学のプロで、
出題者この問題面白そうだけど、
〜中学に過去に出ていた気がする・・・
出題者他の中学の過去問と類似するのは
避けたいから、やめよう・・・
「他校や過去の問題とは異なるタイプの問題」を作成する責務があります。
その中、「新たなタイプ」の問題を作成を試みると、
出題者ちょっとここを
こうひねって・・・
どうしても「難易度が上がってゆく」傾向になります。
こうした「難問」に対して「解法テクニックを多数習得する」勉強の仕方もあります。
「解法テクニックの蓄積」が、「将来大いなる力に結びつくか」は大いに疑問があります。
50~60分の間に、4~5題の難問に対処することは非常に大変なことです。
「ペーパーテストで測れる力」には限界があり、もう少し問題数を限った方が良いように思います。
50~60分の試験時間ならば、「2~3題程度の出題がちょうど良い」ように思います。
出題数を少し少なくして、「深く考えさせる」タイプの問題が増えてゆくことも考えられます。
その方が出題者側としても問題を作成しやすく「将来的に学力が伸びる」志願者を選びやすいでしょう。
食塩水の問題は、文章が長いタイプと短いシンプルなタイプに分かれます。
てんびん算で考える、「食塩の量に着目」か「水の量に着目」など考えられます。
食塩水の問題に限らず「何に着目するのがポイントか」は簡単な絵や図を描くと気付きやすいです。
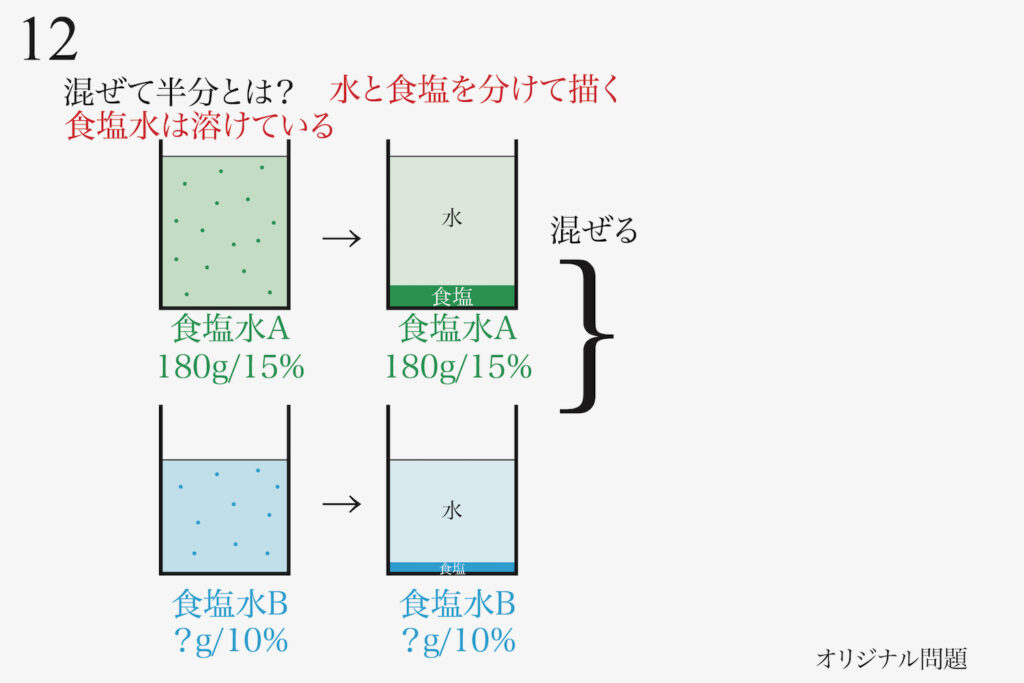
描いてみると気づくことが沢山あります。
てんびん算の問題を解くポイントを、上記リンクでご紹介しています。
文章題を出題して、「状況を図などに整理しなさい」という問題も考えられるでしょう。
「深く考える」問題への対応のためにも、しっかり思考を整理するようにしましょう。
特に難問〜超難問が解けるようになるためには、「解く鍵」に着目することが最も大事です。
・簡単な図や図解を描く
・「溶けている=食塩と水を分離」など分解して「解く鍵」を探す
このように勉強することで試験対策になり、本質的学力の増強も見込めるでしょう。
多数の難しい問題に取り組む受験生の皆さんは、とても大変ですが合格目指して学びましょう。
次回は下記リンクです。
