前回は「文章題のイメージトレーニング〜内容を具体的にイメージ・理解・複数の科目を横断して学力アップ・育む複眼的思考・問題9〜｜中学受験・算数実践27」の話でした。
問題 9（再掲載）
具体的な状況を理解：自分が登場人物になる
今回は解き方を考えてみます。
この文章題の状況を具体的にイメージしてみましょう。
まず、大事なことはなんでしょうか。
男子小学生太郎君が、間違えて
枚数を逆にしちゃったんだよね・・・
「間違えて二種類の硬貨の枚数を逆に計算」が、この問題の大事なポイントです。
つまり、どういうことでしょう。
男子小学生「枚数を逆にした」んだから、
「入れ替えてしまった」ということかな！
具体的に太郎君が硬貨を数えているイメージをしましょう。
男子小学生僕が太郎君になったつもりが、
いいんだよね！
算数の文章題を解く時には、「自分が登場人物の〜だったら」と考えると、イメージ出来るでしょう。
・具体的に状況をイメージ
・「ポイントとなる」ことを探す
・「各科目を横断的に学ぶ姿勢」で、算数以外の学力もアップ
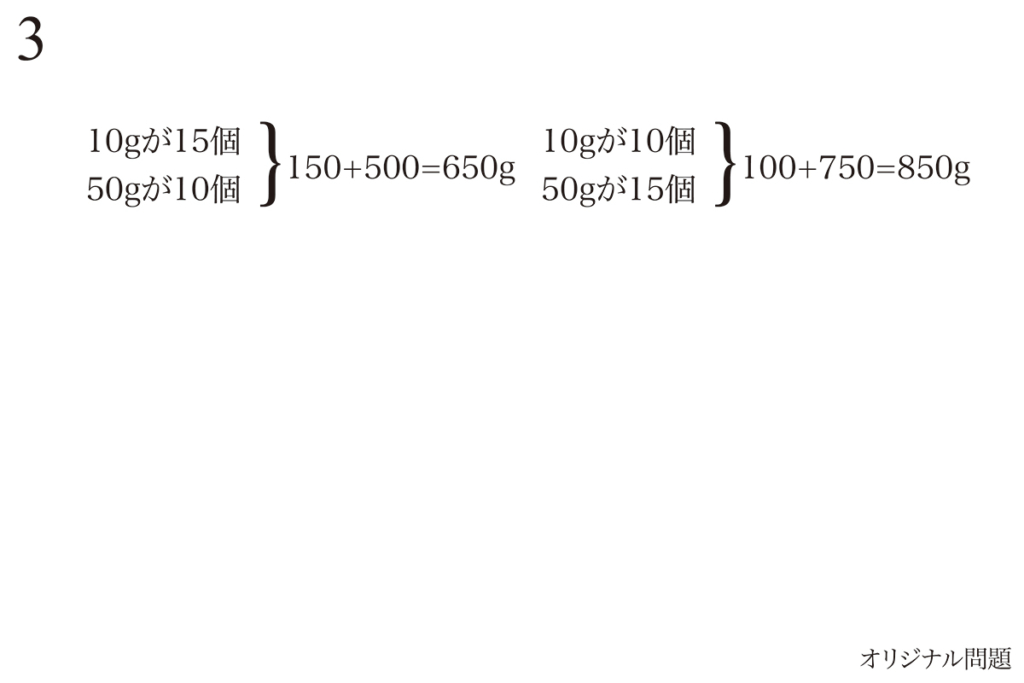
入れ替える問題は、問題3でもありました。（上記リンク）
分かりにくい時は、
男子小学生枚数を逆にしたら、
どうなるのかな？
自分で簡単な実験してみましょう。
女子小学生実験する時は、
簡単な枚数が良いんだよね！
「分からない」から「分かる」へ：考える対象を少なくして実験
今回は、硬貨が3種類ありますが「まずは2種類で考えてみる」ようにしましょう。
女子小学生なぜ、3種類あるのに、
2種類にするの？
3種類を一度に考えるのは難しいです。
ところが、「2種類だったら、だいぶ簡単になる」からです。
・登場する硬貨・おもりなどが3種類（以上）あったら、まず2種類で考える
・自分で具体的・簡単な枚数・数などを設定して実験
例えば、「10円玉10枚、50円玉20枚」で考えましょう。
女子小学生この場合、合計1100円で、
逆にしたら700円だね！
女子小学生逆にしたら、
400円下がった！
この計算の過程で「枚数の違いが問題」と気づきます。
実験する時は、暗算でも出来るくらい「簡単な数字」でやりましょう。
なぜ、400円下がったんでしょうか。
女子小学生10枚と20枚で「共通の10枚」は
計算の時に、同じだった・・・
同じ枚数の10枚は関係なくて、20-10=10枚の違いがポイントです。
そして、「枚数を逆にした時の金額の違い」を生み出します。
女子小学生そっか！
ここで硬貨の金額の違いが影響している！
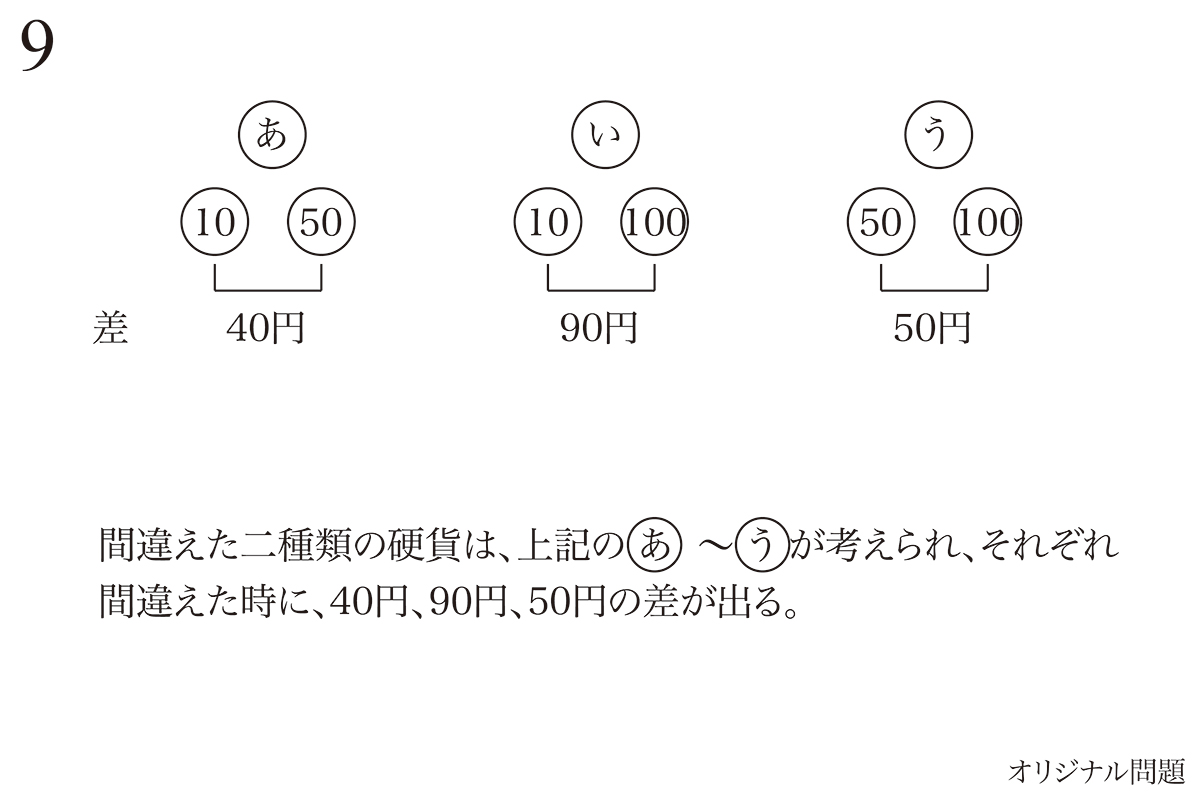
今回は3種類の硬貨があり、逆にするパターンは3種類あります。
上記の通り、あ〜うでそれぞれ逆にした時の差が出ます。
女子小学生3つのパターンで、
それぞれ「逆にする・交換する」と差が違うね・・・
ここからどう考えるか、です。
問題では、「4,260円から3,900円に変わった」です。
女子小学生さっきの「私の実験」では、
「逆にした」ら400円下がったから・・・
女子小学生今回も、
下がる金額が大事だと思う！
「違い＝差」を考えましょう。
差は「入れ替えた1枚あたり金額の差」の倍数になるはず。
そこで、「う」のパターンがなくなり、3パターンから2パターンに絞られます。
整数問題では、すぐに①などの未知数を置かないで、倍数や約数を考えましょう。
男子小学生すぐに未知数を置くと、
行き詰まることがあるね・・・
ここから、「どうやって答え=1パターンに絞る」か考えましょう。
男子小学生う〜ん、
分からないな・・・
わからない時は、とりあえず①など未知数を設置してみましょう。
文章題の内容・条件を全て把握：文章にマーク
とりあえず、二つの場合で、各枚数が出てきました。
さあ、ここからは何がポイントか、考えてみましょう。
「使ってない問題の条件」があるかどうか、は大事な視点です。
文章題では、大事なポイントにマルなどマークしましょう。
そして、「出てくる条件を全て理解」するようにしましょう。
・しっかり状況をイメージ・理解
・出てくる状況・条件などをマルなどでマーク
理科の実験問題のコツの話を、上記リンクでご紹介しています。
理科の実験問題などでも、「大事な数字」や「状況が変わるポイント」をマークすると良いでしょう。
女子小学生考えていない
条件・・・
女子小学生あった！
「間違えた二種類ではない硬貨の枚数=奇数」だ！
「奇数か偶数か」は大きな条件です。
男子小学生確かに「奇数」か「偶数」は、
大事！
奇数は一つに絞られます。
穴埋め式だったら、
男子小学生こっちだ！
余白に○を書いて進めます。
記述式の場合もきちんと文章にせず、下記のように簡潔に表現しても良いでしょう。
記述式などでは「偶数-偶数=偶数」「奇数-偶数=奇数」と書くと丁寧で、採点者は、
採点者ちゃんと
分かってるね！
このように感じてくれて、好感を持ってくれるでしょう。
「わかっていること」は走り書きでも、メモの形式でも良いですから、書きましょう。
整数問題：差を考える・奇数と偶数
ここまで来たら、あとは立式して計算すれば解けます。
合計で4,260円、二種類入れ替えたら3,900円など「比較的大きな数字」が出てきている時。
その時は、差をとってみましょう。
整数問題で、和・差を取ることは本質的なことで、なんらかの特徴が出てきます。
この場合、4260-3900=360を考えると、
男子小学生少し
楽になる気がする・・・
考える対象が一桁小さくなるのが大事で、ずいぶん扱いやすくなります。
女子小学生あ、そうか。
確かに、桁が小さくなると簡単に見えるね！
これで、非常に問題が考えやすくなります。
そして、問題3と本問のように、「入れ替えたら」という問題が出たら、
女子小学生あっ、
差が大事！
このように「入れ替えた結果の差」に注目すると良いでしょう。
いくつか整数問題取り上げましたが、これで大抵の整数問題は解けると思います。
「整数問題→倍数・約数・和・差を考える」を、きちんと頭に入れておきましょう。
次回は下記リンクです。
