前回は「文章題をしっかり理解する姿勢〜・整数の性質・倍数・比・問題6〜」の話でした。
今回は解法Aの話です。
問題 6（再掲載）
ある小学校の男子生徒、女子生徒の比は16:15です。
3年生から6年生まで各学年の人数は同じですが、最近新しいマンションが建ったので人口が増えました。
そして、他の学年より1年生は42人、2年生は24人多いです。
ある日、全校生徒が21台のバスで遠足に出かけました。
全てのバスには同じ人数が乗りました。
全校生徒は2000人以下です。1年生の生徒は何人ですか。（オリジナル問題）
条件を整理して未知数を設定：解法A
3つの条件が、出てきます。
それぞれに対して、未知数を設定して整理してみましょう。
全校生徒の人数が3つの式で表され、それらが等しいです。
これらが等しい条件を等式にして、比較します。
これでは、
求まらないんじゃない？
確かに、この式からは答えを求めることができません。
分からないもの（未知数）が3つあったら、3つの独立した等式が必要です。
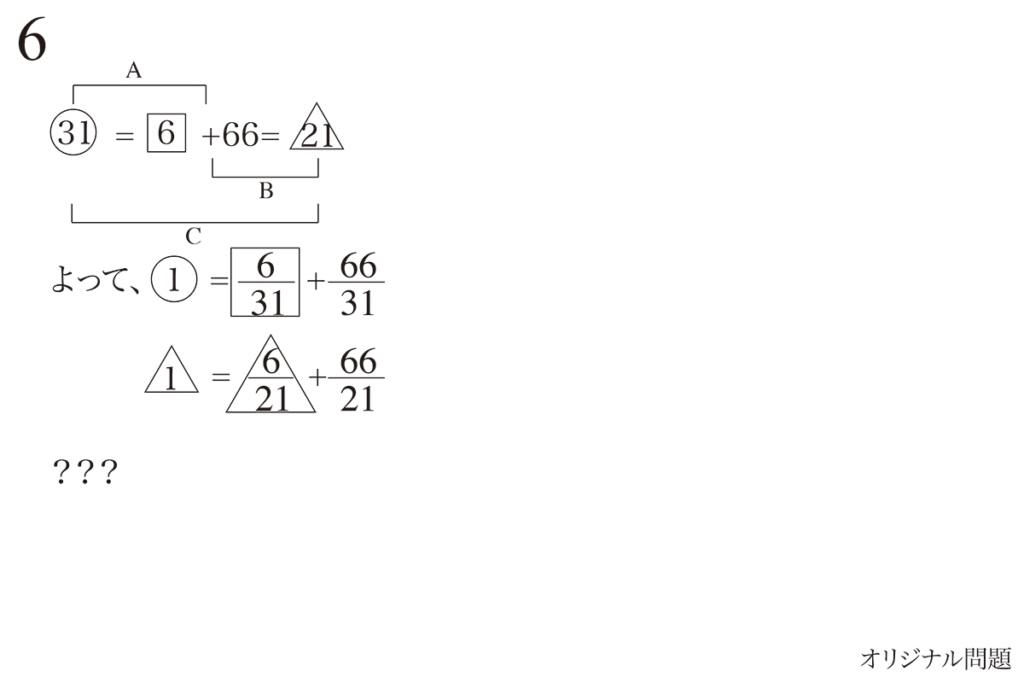
A,Bの等式から条件式を求めましたが、CはA、Bから導かれます。
3つ独立した等式ではなく、2つの等式しかありません。
本当に、A,Bの等式からCが出てくるか、実際に計算して試してみましょう。
同様に、AとCからBが出てくることも確認してみましょう。
なぜ、こういうことになったのでしょうか。
上の条件式では、設定した分からないもの（未知数）が整数でなくても良いのです。
人数は整数ですから、「整数であること」の条件を使いましょう。
男子 : 女子の比とバスの台数から、全校生徒の人数は31と21の倍数です。
倍数を考える：「整数であること」を活かす
全校生徒は3通り考えられます。
ここからは、一学年の人数を設定してみましょう。
それぞれの場合で計算して、整数となる解を選んで、答えに至ります。
約数を考える：解法B
整数問題の基本は、倍数や約数を考えることです。
上記の回答でも良いですが、ある本質的なことに気づくと、少し簡単に解けます。
整数であることをより意識して、倍数を考えてみましょう。
解法Bは次回ご紹介します。
