前回は「文章題が「苦手」から「得意」へ〜「入れ替える」ことを具体的に考える・頭で考えすぎず手を動かす・どういうことか理解する・問題3〜」の話でした。
問題3(再掲載)

文章題のおすすめ考え方・解き方:実験して考える

「分からないものが2つ」だと、分かりやすいです。
「分からないものが3つ以上」になると、急に難易度が上がります。
中学受験では「分からないものが4つ以上」は出題されないでしょう。
そこで、「分からないものが3つ」でも慌てない姿勢が大事です。
大勢の方が「苦手」と感じる電気・電流は、「電圧・電流・抵抗の3つ」が登場します。
「考える対象が3つ」になると、複雑な感じになりますが、具体的に考えてみましょう。
 男子小学生
男子小学生う〜ん・・・
分からない・・・
少し手が止まるかもしれません。
すぐにパッと、解く鍵が見つかる場合は良いです。
悩むときは「自分で簡単な場合をつくって、考える」をやってみましょう。
いわば、実験してみるのです。
簡単な場合を考える:状況をしっかり把握
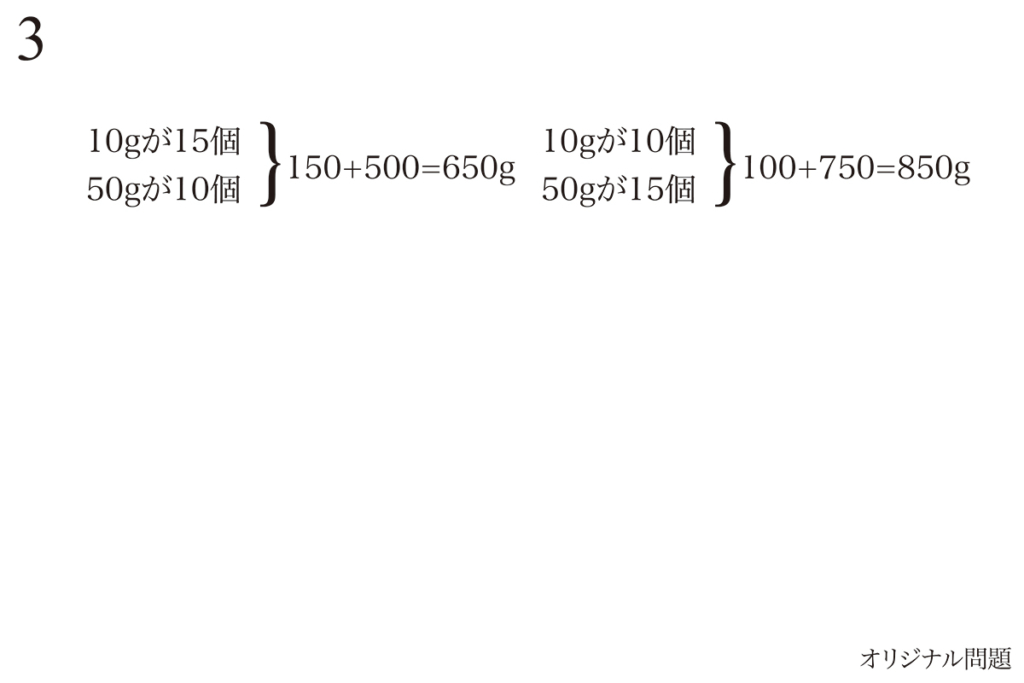

10gと50gのおもりを入れ替えることがポイントなので、この二つを考えましょう。
例えば「10g:10個、50g:15個→合計850g」となります。
入れ替えると「10g:15個、50g:10個→合計650g」です。
入れ替えたら、どうなりましたか。



200g
減ったね!
実際に計算してみましょう。
10 x 10 + 50 x 15 =850
10 x 15 + 50 x 10 =650
「数を入れ替えると言っても、共通する数(この場合10個)は影響がない」と気付きます。
差の200gは「50gと10gのおもりの差の40g」が関わっていそうです。
ここで、



あっ、
ひょっとして・・・
と気づく場合があります。
実験する時は、暗算で出来るくらいな簡単な設定にしましょう。
よく分からない文章題や数列に出会った時、「実験してみる」のは本質的で、難問では有効な場合が多いです。
まずは状況をしっかり把握することから始まります。
「自分の実験」と答案:考えていることを答案にアピール


解法に行く前に「試験において」の話です。
実際の試験において、上記のようなメモは問題文の余白にすることが多いでしょう。
答案用紙でやっても良いでしょう。
例えば、答案用紙の端に上記の「自分の実験」を書いたとします。
そして、ここで実験したら、



よし!
これで分かったぞ!
それから本題に入っても良いのです。
綺麗に描かなくても、走り書きでも良いでしょう。



余計なことを書いたら、
減点されるのでは・・・
こう懸念する方がいらっしゃるかもしれません。
採点者の判断によりますが、記述式の問題では「減点はしない」と考えます。
不安でしたら、下記のように[ ]で閉じたり「草案ですよ」というマークをしても良いでしょう。

どんな問題でも、解法のポイントがあります。
「大事なこと・ポイントに気づくこと」は「きちんと解答に辿り着くこと」の大きな部分を占めると言えます。
大事なことに気づけば、ある程度の点数はもらえるでしょう。
大抵、これらのメモを答案は試験用紙の余白に書きます。
記述式試験の場合、余白でなく小さく答案の端に「ちょっと書く」感じでも良いでしょう。
こういうメモは、「小さめの文字で簡単に書く」のが良いです。



大きい文字で
書いたら・・・



本題の答案を書く場所が、
なくなってしまった・・・
あまり大きな字で書かずに、、適切なサイズの字で書く様にしましょう。
大きく書く・描くことは大事なことです。
試験では「試験答案」という世界があるので、「その世界の中でおさめる」ようにしましょう。
解法がすぐに思いつけば、すぐに本題の解法に入れば良いでしょう。
これを「答案用紙に書くこと」の意味は、採点者に「一生懸命考えています」とアピールすることです。
記述問題のコツの話を、上記リンクでご紹介しています。
大学生の時、塾のクラス分け試験やテストゼミの数学の採点をしたことがあります。
記述式の場合、必ず部分点があります。
部分点は「ここまで出来たら〜点」みたいな基準がありますが、採点者の裁量で多少は上下します。
そうすると、やはり「頑張ってポイントに気付こうとしている人」には点を上げたくなるのが人情です。
上記のような、メモがあるだけの答案を見た採点者はどう感じるでしょうか。
大事なことに気付こうと努力している姿は、微笑ましいでしょう。



あっ、ポイントに
気付きかけているな・・・
採点者がこう考えれば、1点か2点、場合によってはもう少し点を上げることがあるでしょう。
白紙答案であれば、



白紙だったら
✖️しかつけようがない・・・
「0点をつける」しか方法はないのです。
「解く何らかのキッカケを探そうと努力して、気付きかけている」ことをアピールする事は大事です。
特に、時間制限のある試験では大きな意味のある事だと思います。
「大事な差」に着目


先ほどの「実験」で、大事な事に気づきました。
総重量が減ることは「50gのおもりの方が多く」「差の40gがその差を生む」事です。
問題3では総重量が360g減少し、その原因は一つあたり50-10=40gです。
そこで、360/40=9個の分だけ、50gのおもりが多いです。
これで、だいぶ見えて来ました。
分からない10gのおもりの数を①とおいて、下記の通り10gのおもり15個と分かります。
答えは、10g:15個、20g:11個、50g:24個です。
10g:15個
20g:11個
50g:24個
最初の「360gの差」が問題の本質的部分ですが、その後は少し違った見方が出来ます。
次回ご紹介しますので、少し考えてみて下さい。
ヒントは「平均」です。
次回は下記リンクです。



