前回は「国語力・読解力と文章題の解き方〜具体的な状況を理解・自分が登場人物になる・「分からない」から「分かる」へ・考える対象を少なくして実験・文章題の内容・条件を全て把握・文章にマーク・整数問題・差を考える・奇数・偶数・問題9解法A〜」の話でした。
問題 9(再掲載)

棒グラフと平均を考える姿勢:解法B

今回は別の考え方で解いてみましょう。
今回は、少し異なる視点で考えてみましょう。
途中まで前回と同一で、「あ、い」の2パターンに絞られます。
前回は、ここから未知数を設置して解きました。
今回は、未知数を設置しないで解いてみましょう。
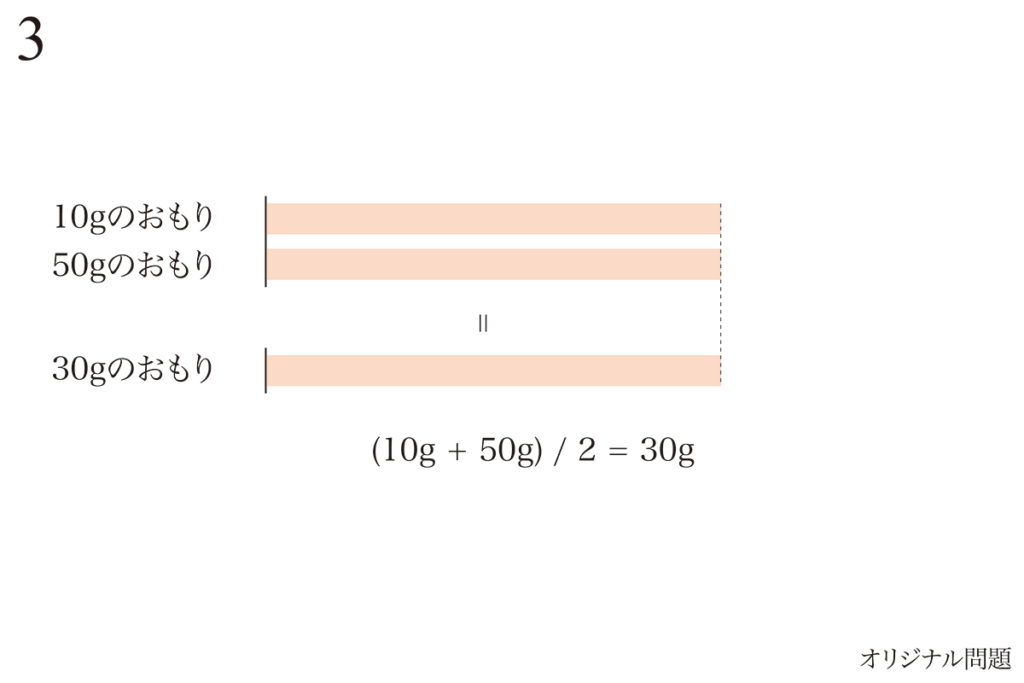
問題3の解法で、二つのおもりの平均をとって「まとめる」解法をご紹介しました。(上記リンク)
同様な考え方で、(い)の場合から考えてみましょう。
棒グラフを書いてみましょう。
この時、「100円玉の方が10円玉より4枚多い」以外に、50円玉の枚数がわかりません。
 男子小学生
男子小学生棒の長さを、
どうするか?
「長さはどのくらい?」と考えてしまうかもしれませんが、わからないので、適当な長さで良いです。
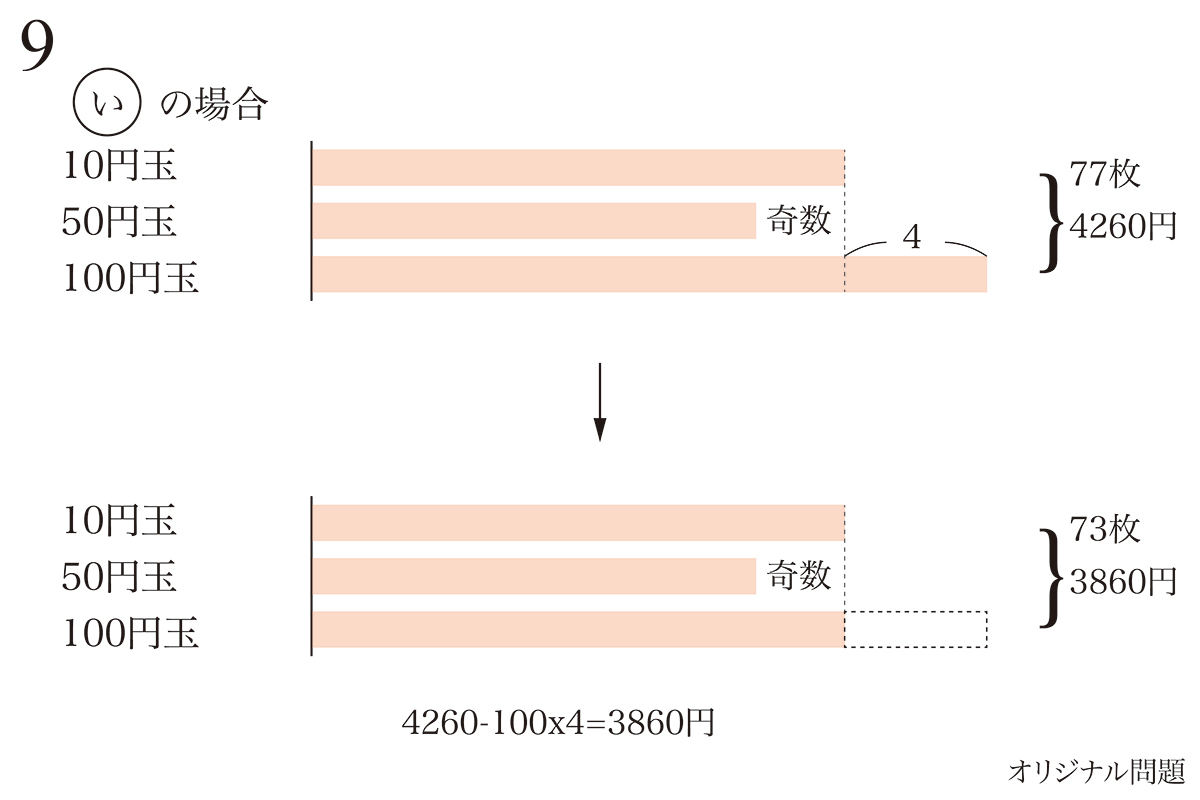

時には「適当に考えて進む」事も大事です。
分かりやすくするように、「差の4枚」をカットして枚数と総額を減らします。
「10円玉と100円玉の個数が同一」になったので、これらの平均をとれば、一つにまとめられます。
2つを1つにまとめる発想:考える対象を減らす
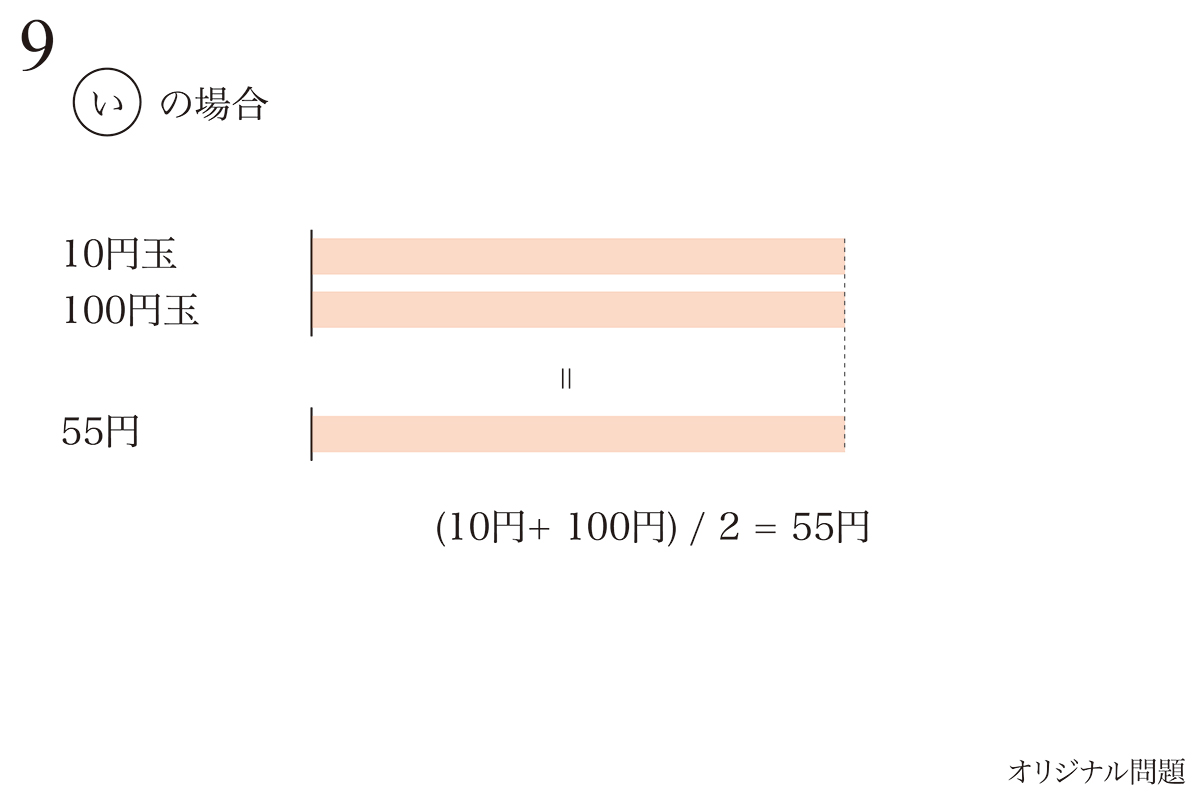

55円玉はありませんが、10円玉と100円玉の分が、55円にまとめられました。
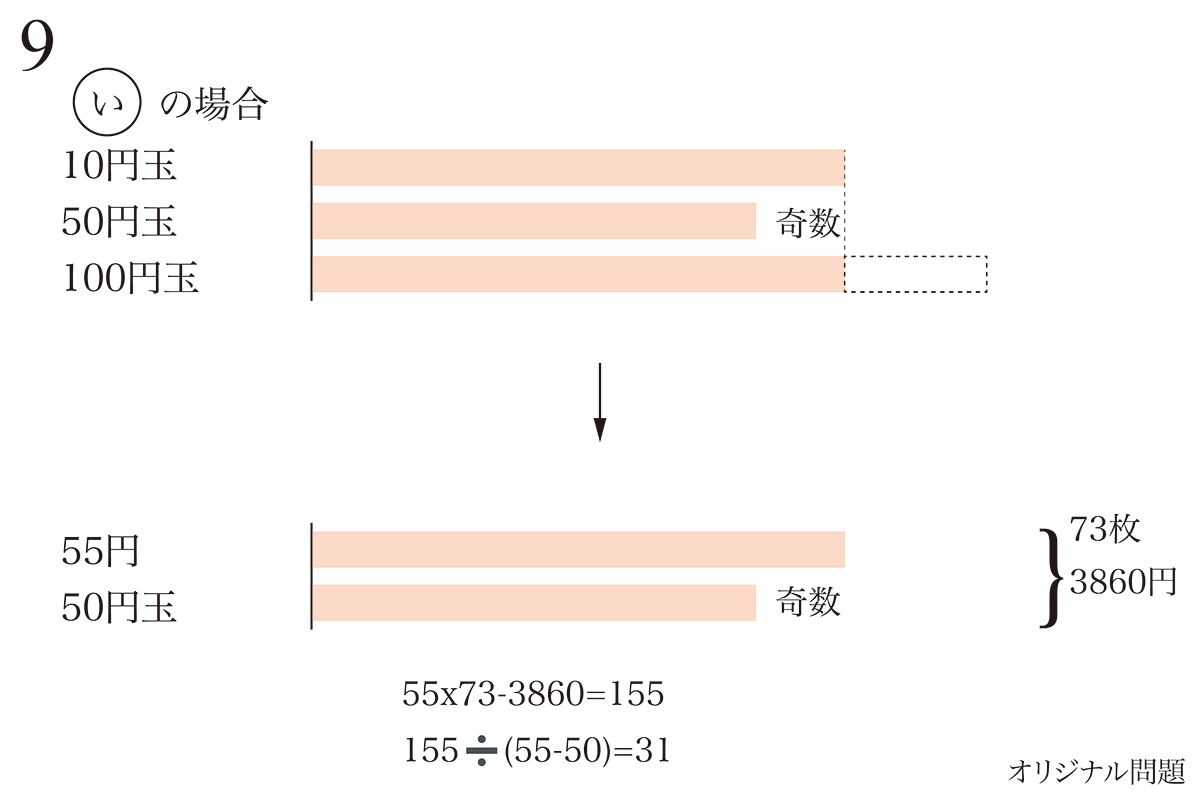

対象が3つから2つになると、あとは鶴亀算です。
50円玉が31枚と分かり、確かに奇数ですからOKです。
すると、55円は残り42枚ですから、10円玉は21枚となります。
「対象が3つある」と、考えるのが難しいです。
このように「平均をとる」ことで、「2つを1つにまとめる」ことは非常に本質的な考え方です。
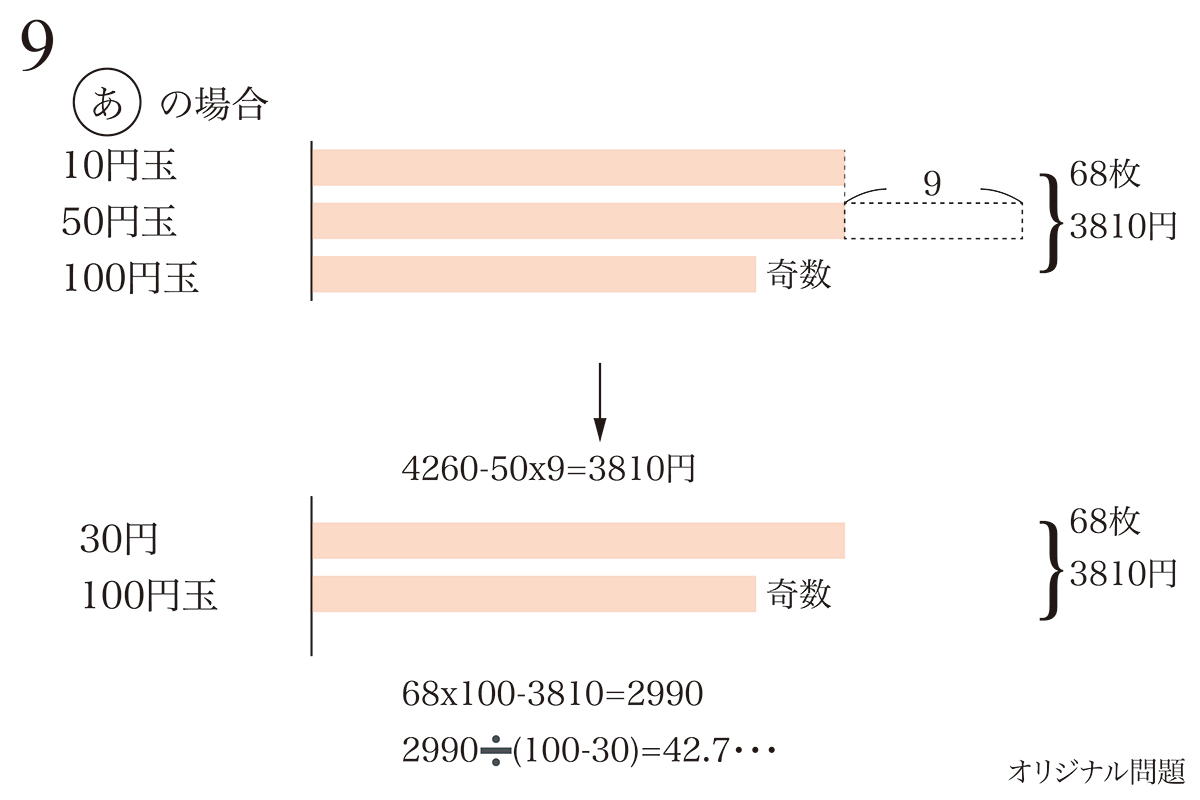

同様に、(あ)を考えましょう。
(あ)の場合、鶴亀算で考えると「整数であるべき枚数」が整数になりませんから、ここで✖️となります。
「入れ替えていない硬貨の枚数が奇数」は条件としてなくても、解けることになります。
これは、僕が前回の解法のように考えて、奇数か偶数かを考えた結果でした。
前回の考え方も大事ですから、押さえておきましょう。
大事な平均


平均を取って「2つ以上の対象をまとめる」考え方は非常に有効だと思います。
解法Aのように「未知数を設定する」ことは、整数問題では決定打にはなりにくい場合があります。
そのため、この解法Bの方が良い面があります。
問題3でも書きましたが、対象が2つであれば易しいのです。
ところが、対象が2つから3つになると「変化するものが3つ」となり、途端に扱いづらくなります。


電流・電圧・抵抗の3つが登場する電気の問題は、苦手意識を持つ方が多い分野です。
それは、「電流・電圧・抵抗の3つが登場」するからで、



3つも考えるのは、
ちょっと大変・・・
考える対象が多いから、難しく感じられます。
そこで、電気の問題では、「主役は電圧」と考えることが大事です。
「平均を考える」ことは対象を絞ることになり、スッと解きやすくなる場合が多いです。
例えば「1から10の整数の和」を考える時、



最初の1と最後の10の
平均は5.5だから、



5.5を個数分10かけて、
5.5×10=55
このように考えることも出来ます。
整数問題に限らず、



どれか、
まとめられないかな・・・
「平均を取る」などして、まとめると分かりやすくなる場合が多いので、お勧めです。
次回は下記リンクです。



