前回は「複数の同じ図形の問題を考えるコツ・ポイント〜図形の基本性質に着目・2つの正方形は同じ性質・「正方形とは何か」を考える・描く・「固定された点や線」に着目・少し考えてみる大事さ・「急がば回れ」で学力向上・問題 13(2)解法〜」の話でした。
問題 13
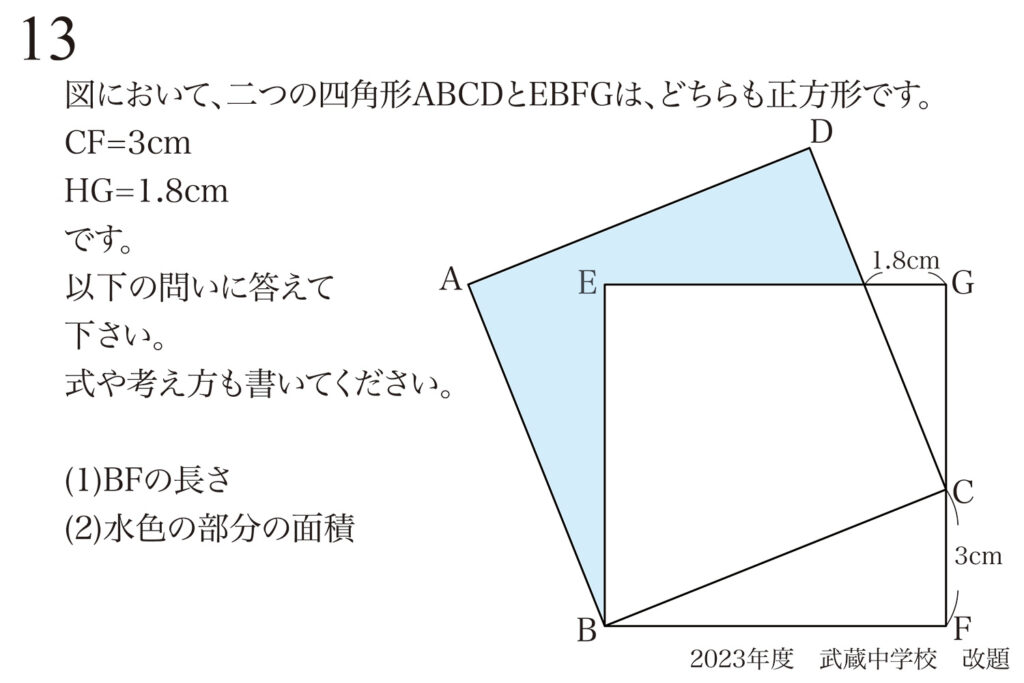
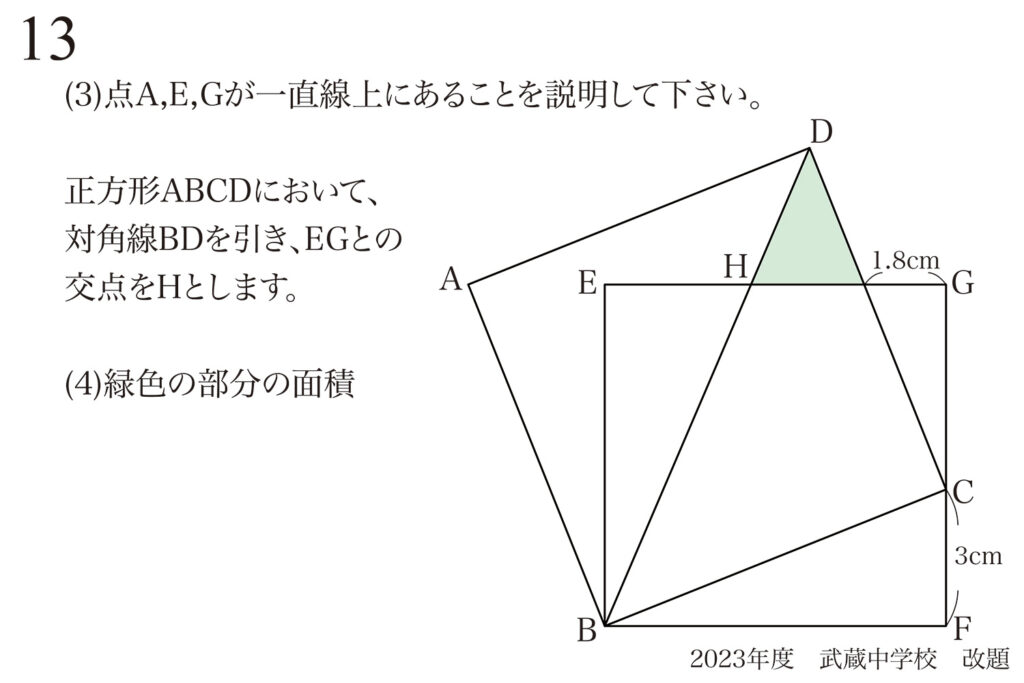
矢印で図形問題を攻略するコツ・ポイント
「矢印」の考え方から、今回の問題を考えてみましょう。
「矢印」の考え方は、高校数学で勉強する「ベクトル」の基本です。
男子小学生えっ？
ベクトル・・・？
男子小学生なんか、
難しそう・・・
ベクトルは、完全に小学校の算数の課程外です。
そのため、小学生は「ベクトル」という言葉も知らなくて大丈夫です。
女子小学生知らなくて
いいの？
ここでは「ベクトル」という言葉を紹介しただけです。
男子小学生なんか、かっこいい
名前だね！
本格的には、中学生・高校生で勉強することを楽しみにしてください。
ここでは「ベクトル」という言葉は忘れて、「矢印」で考えてみましょう。
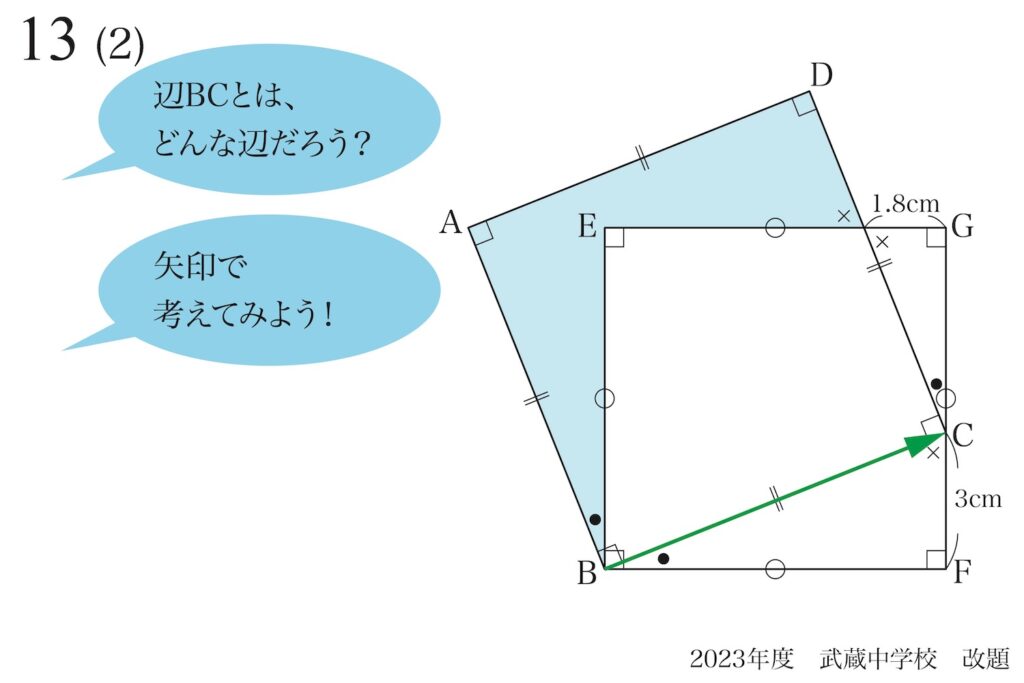
辺BCを「矢印BC」と考えてみましょう。
そして、矢印BCを「二つの矢印に分けて考える」ようにしてみましょう。
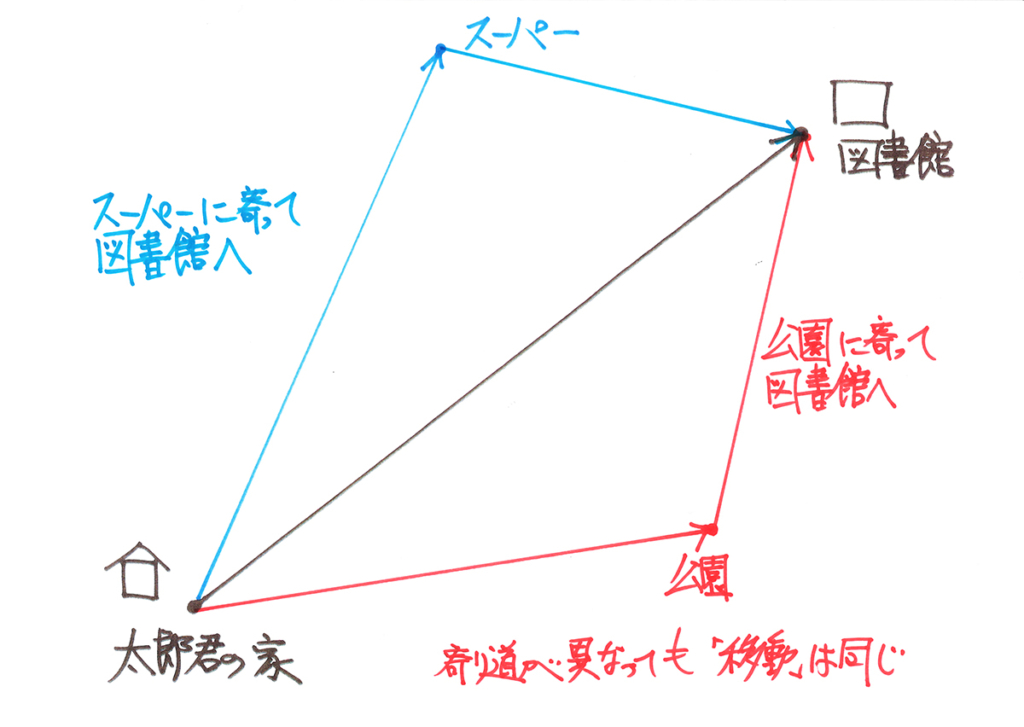
上の図と同じように「寄り道」で考えてみましょう。
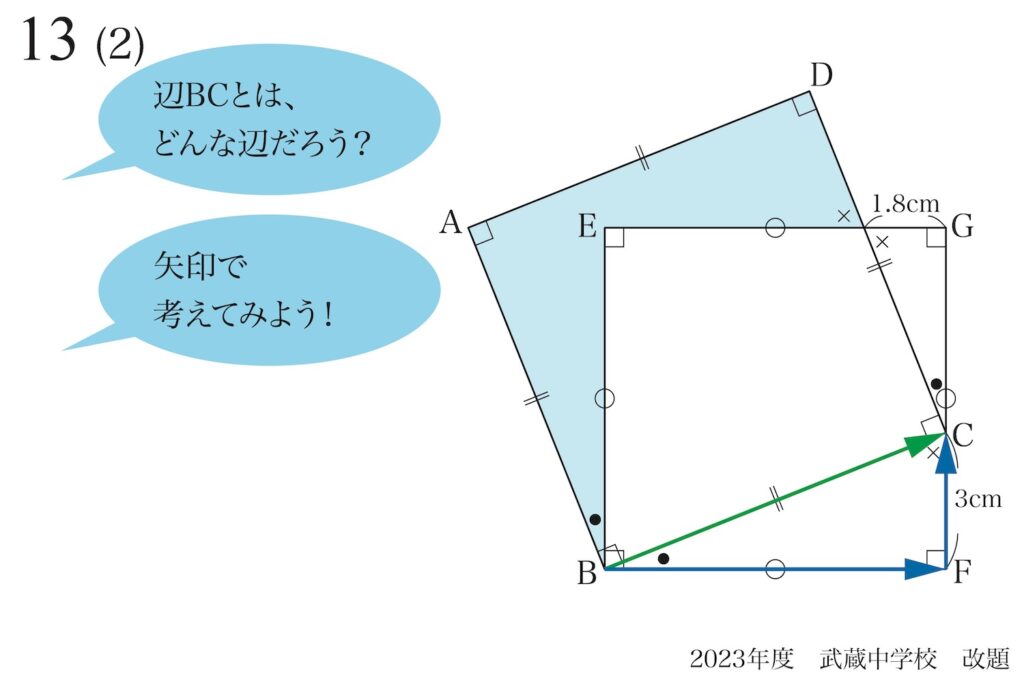
男子小学生同じように矢印を組み合わせて、
「寄り道しても同じ」だね！
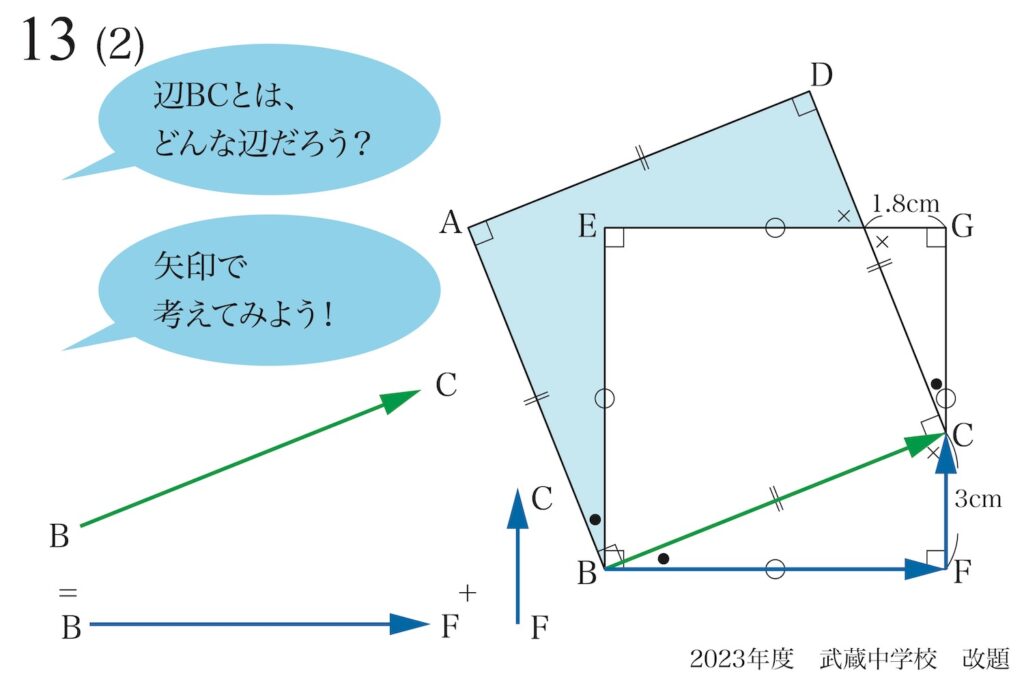
「矢印BC=矢印BF+矢印FC」となります。
自分の手で描く大事さ：水泳と勉強は同じ
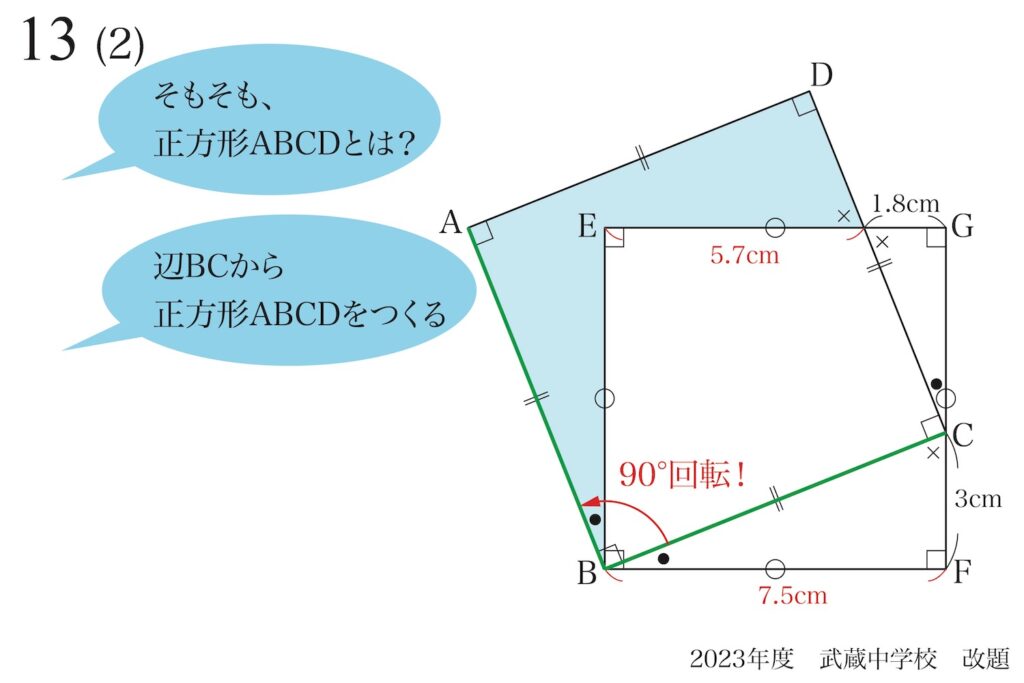
前回、「正方形ABCDを辺BCからつくる」ことを考えました。
同じように、矢印ごと辺を回転してみましょう。
ちょっと自分で描いてみてください。
女子小学生上手く
描けるかな・・・
絵や図は「上手な方が良い」ですが、それを気にしていると「描けなくなる」のです。
画家などの美術家を目指している方は別かもしれません。
算数や理科では「下手でも良い」くらいな気持ちで描きましょう。
描いているうちにコツが掴めてきて、少しずつ上手になってきます。
でも「描かないと上手にはならない」のです。
これは、水泳などと同じです。
水泳と学びの比較の話を、上記リンクでご紹介しています。
「畳の水練」という言葉があります。
本を読んだりするだけで「水泳が上手になること」は絶対にないでしょう。
女子小学生確かに
そう！
何はともあれ「実際に水の中に入って泳いでみる」ことをしなければ、水泳が上手になることはないです。
それと同様で、「描いてみることなしに、描くことが上手になる」こともないのです。
矢印ごと回転：分かったことを図形に描きこむ
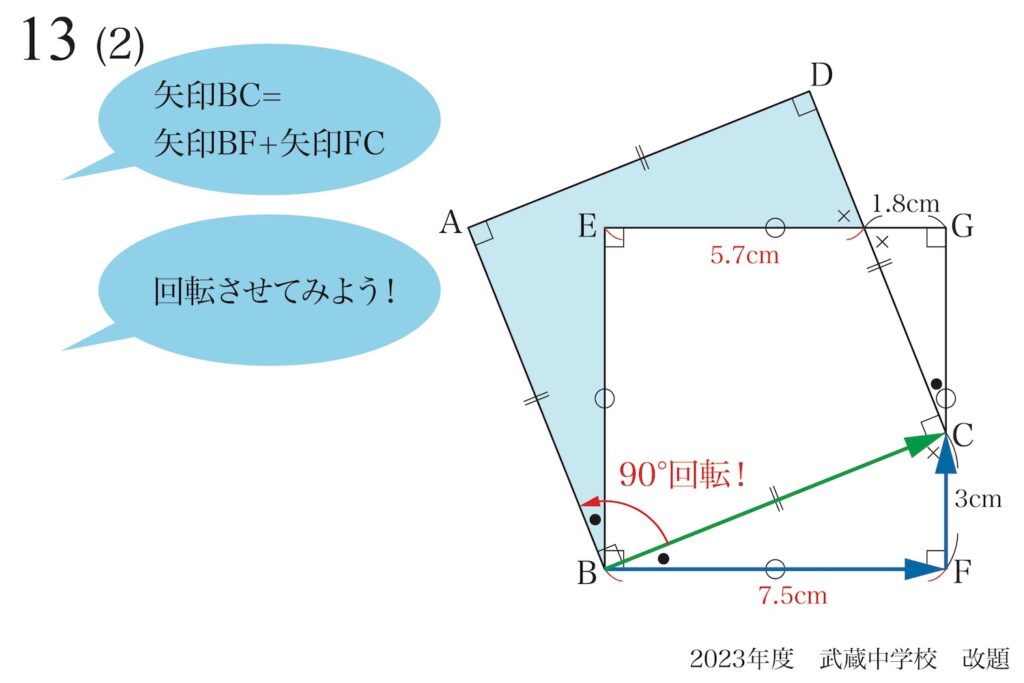
3つの矢印をエイっと90度回転してみましょう。
男子小学生ということは、
矢印の三角形ごと回転させるのかな・・・
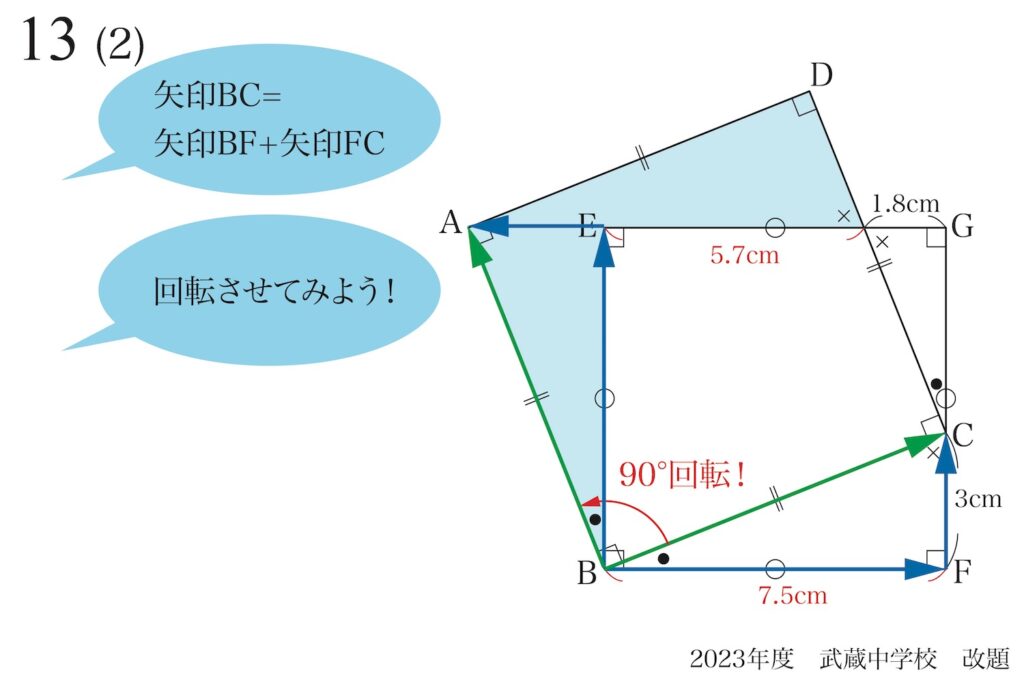
ここで、
男子小学生あっ、
ひょっとして・・・
あることに気づいた方も多いでしょう。
気づかなかった方は、もう少し図形問題を考えてみると分かるようになるので進んでみましょう。
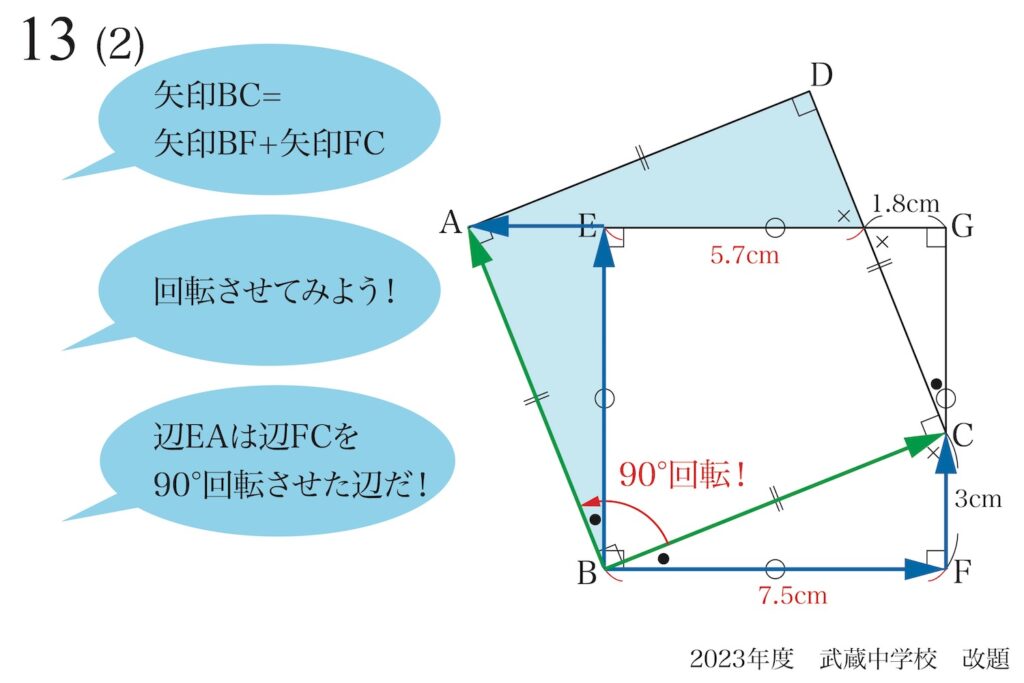
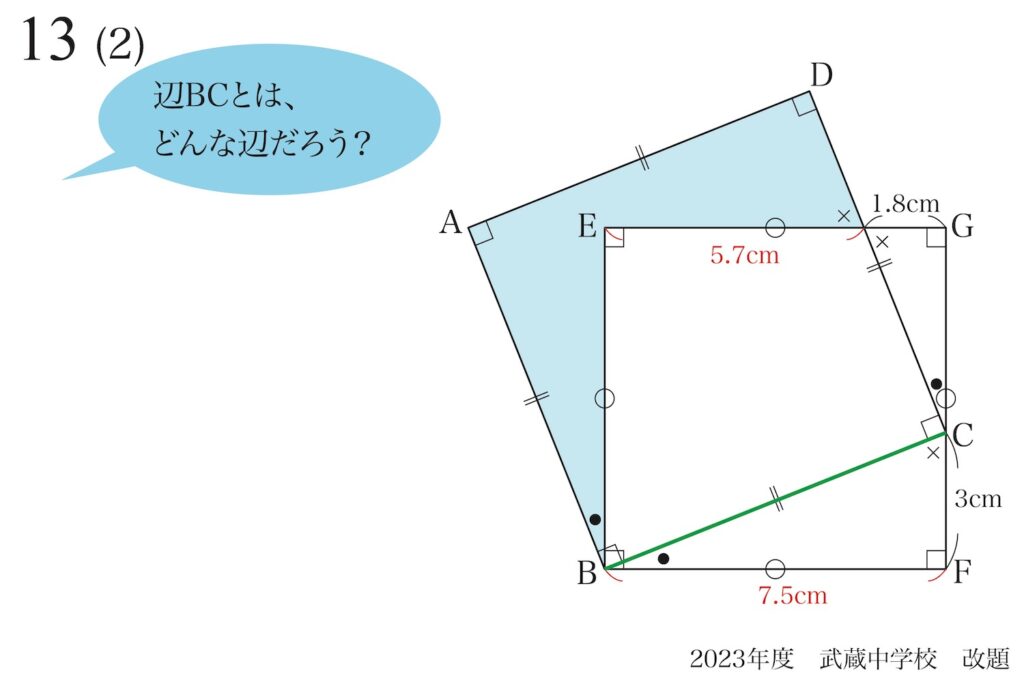
「辺EAは辺FCを90°回転させた辺」であることが分かります。
このことが、この問題の大事なポイントです。
「△BFCと△BEAが同じ（合同）」であることが分かります。
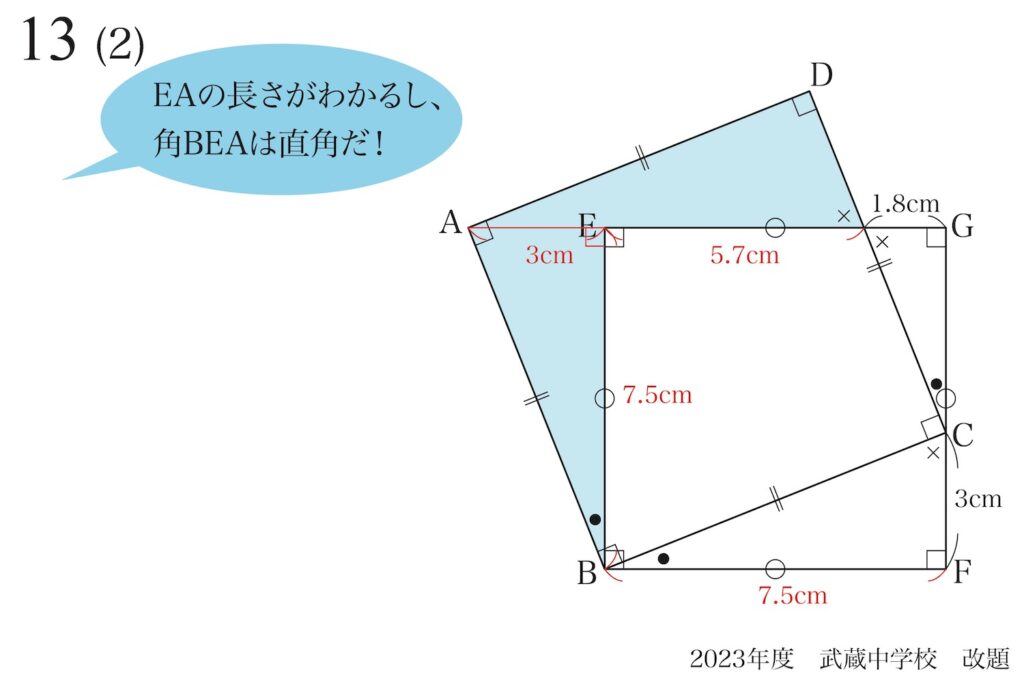
これで、EAの長さと角BEAが直角であることが分かりました。
このように「分かったこと」は、図形にどんどん描いてゆきましょう。
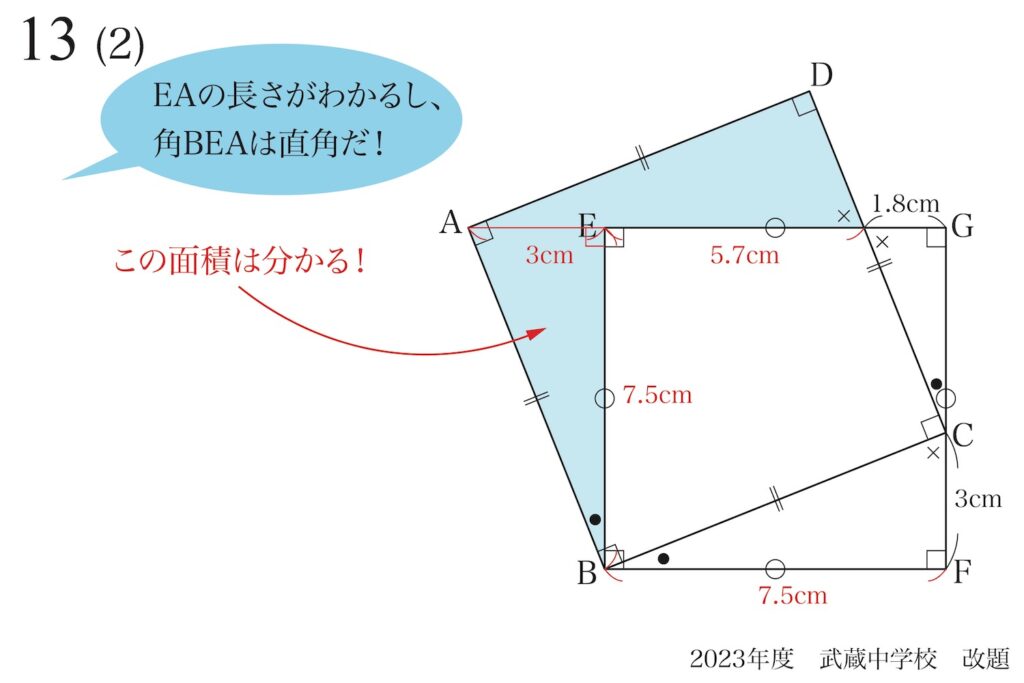
これで、直角三角形BEAの面積がわかるので、一歩前進です。
このように図形問題でも他の分野でも、算数の問題を解いているときは一歩前進したら、
男子小学生これで、
答えに近づいているはず！
「答えに辿り着ける」気持ちを強く持ちましょう。
・「問題文に記載されていること」と「分かったこと」は「図形に描きこむ」など明確に意識
・一歩前進したら「答えに近づいているはず」という気持ちを強く持つ
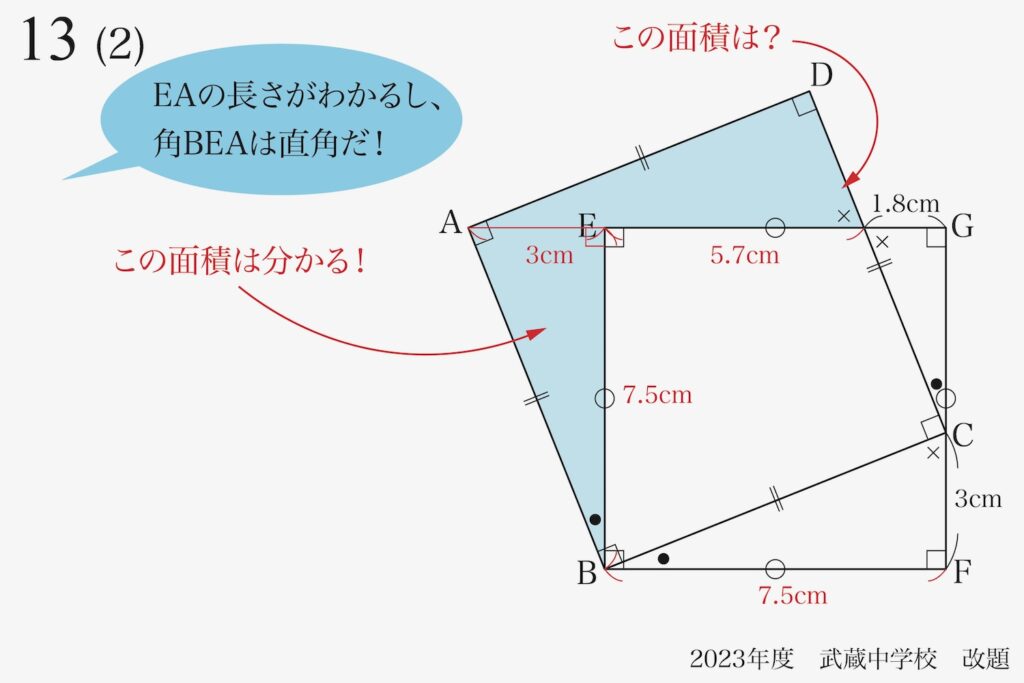
そして、問題の青色の面積を求めるには、もう一つの三角形の面積がわかると良さそうです。
図形のどこに着目するか：「分かっていること」を大事に
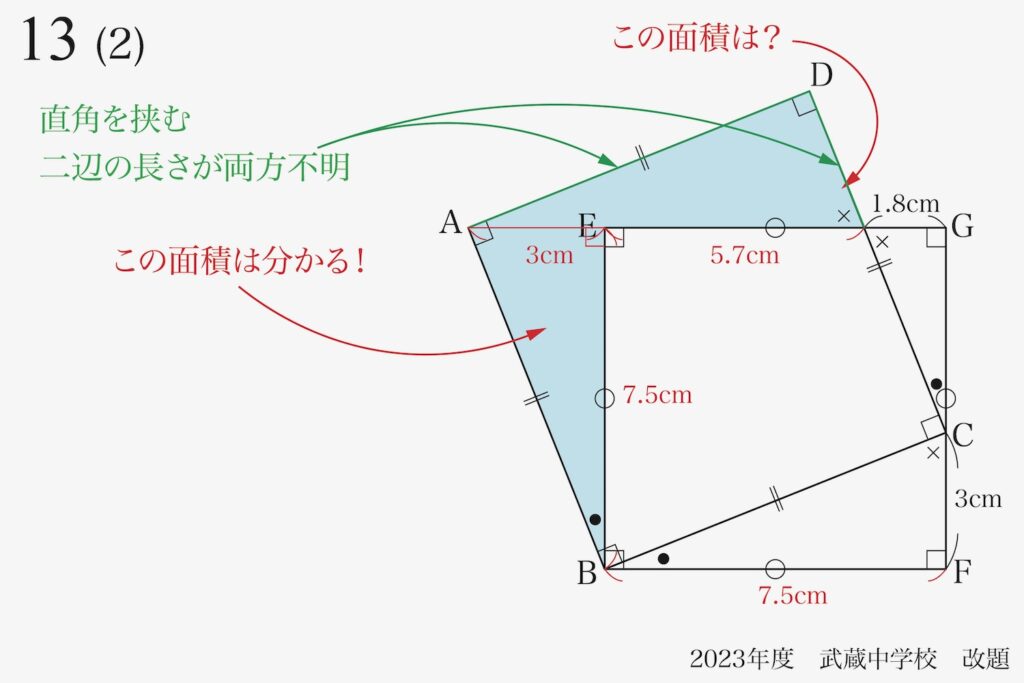
こちらの三角形は直角三角形なので、「直角を挟む二辺の長さが分かれば面積が計算可能」です。
ところが、「直角を挟む二辺の長さ両方が不明」です。
このように「わからない辺（こと）が二つ残っている」ときは、
男子小学生両方の
辺の長さを求めよう！
このように考えずに、
男子小学生別の方法で、
三角形の面積が求まらないかな・・・
「違う方法」や「異なる視点」を考えるようにしましょう。
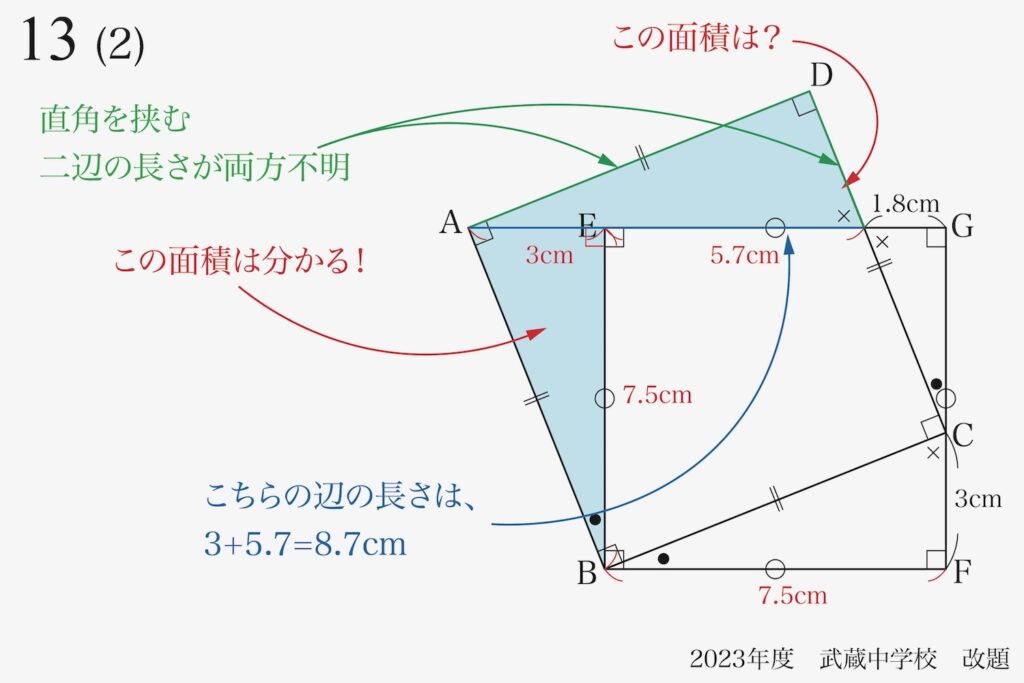
この直角三角形は斜辺の長さは、辺の長さを足せば求まります。
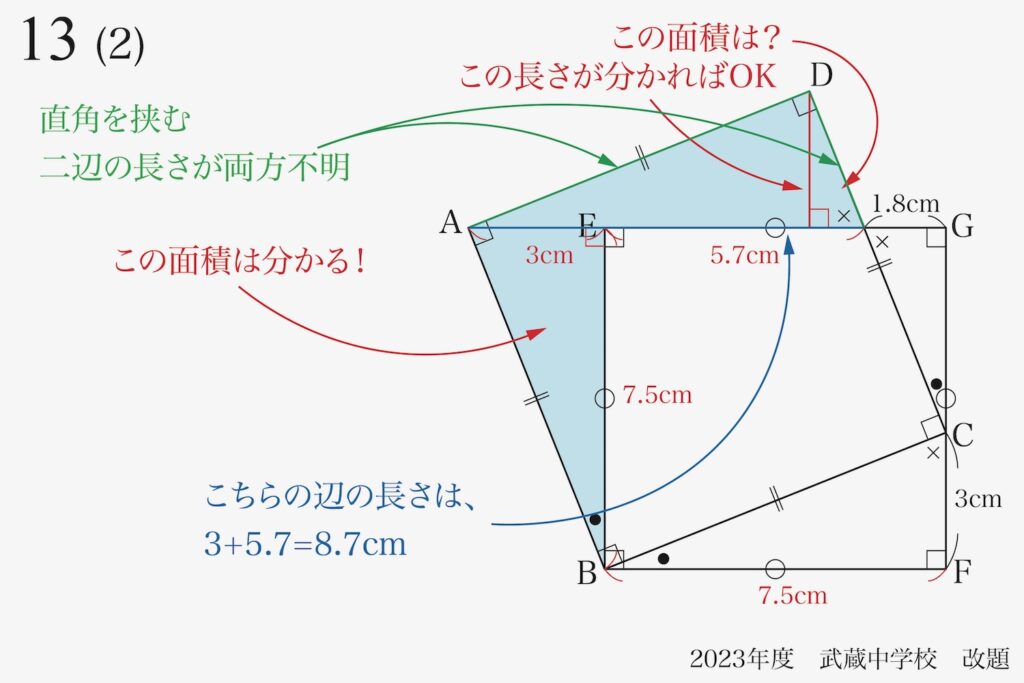
ここで、Dからこの斜辺に垂直に線を下ろす（垂線）ことを考えてみましょう。
「赤線の長さ」が分かれば、上の三角形の面積は求まりそうです。
このように「分かっていることを出来るだけ活かす」ことを大事にしましょう。
・直角三角形や正方形など「直角がある図形」の面積は、「直角を挟む辺の長さ」が大事
・「直角を挟む辺の長さ」が分からない時は、「分かっていること」を出来るだけ活かす
ここで、
男子小学生どうしたら
面積求められるかな・・・
手が止まってしまう方もいるでしょう。
そういう時は、
男子小学生もう少し
同じ角度はないかな？
同じ角度や同じ長さを探してみましょう。
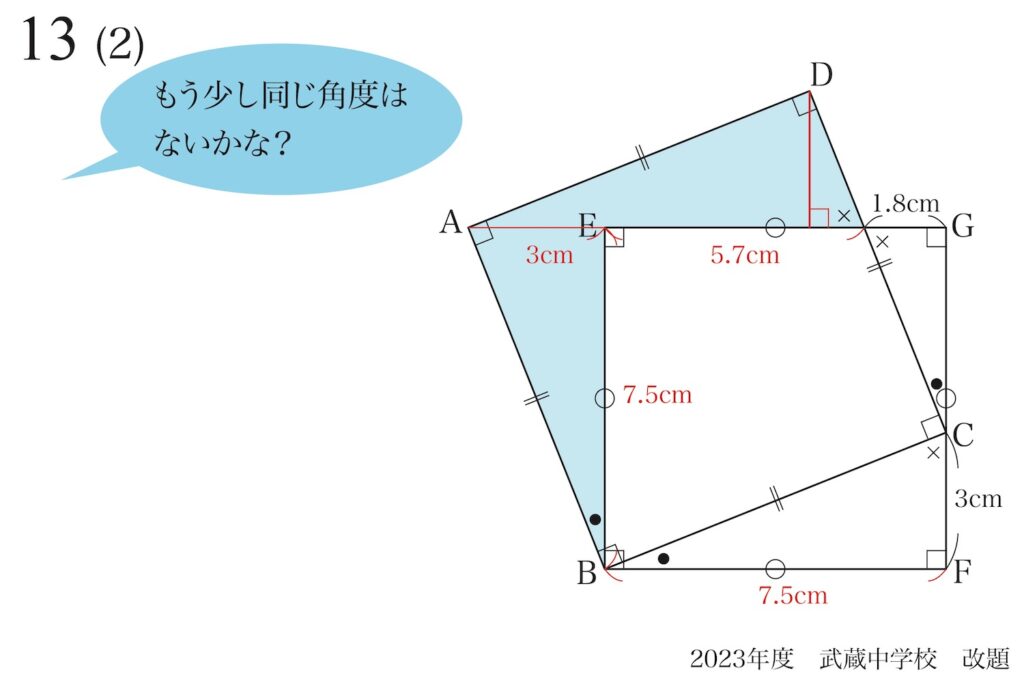
(2)の問題はもう少しです。
上の話でご紹介した通り、図形問題では「分かったこと」が活かせるように考えることが大事です。
次回は、一気に答えまで到達しましょう。
次回は下記リンクです。
