前回は「回転移動する図形が得意になる考え方〜いつも平行な辺を探す姿勢・「平行な辺」と相似図形・前の問題で考えたこと・解いた結果を意識・後の問題のヒント・相似から辺の比を考える姿勢・問題 8(2)解法〜」の話でした。
問題 8（再掲載）
面積比：相似比を2回掛ける・2乗
今回は(3)の解法です。
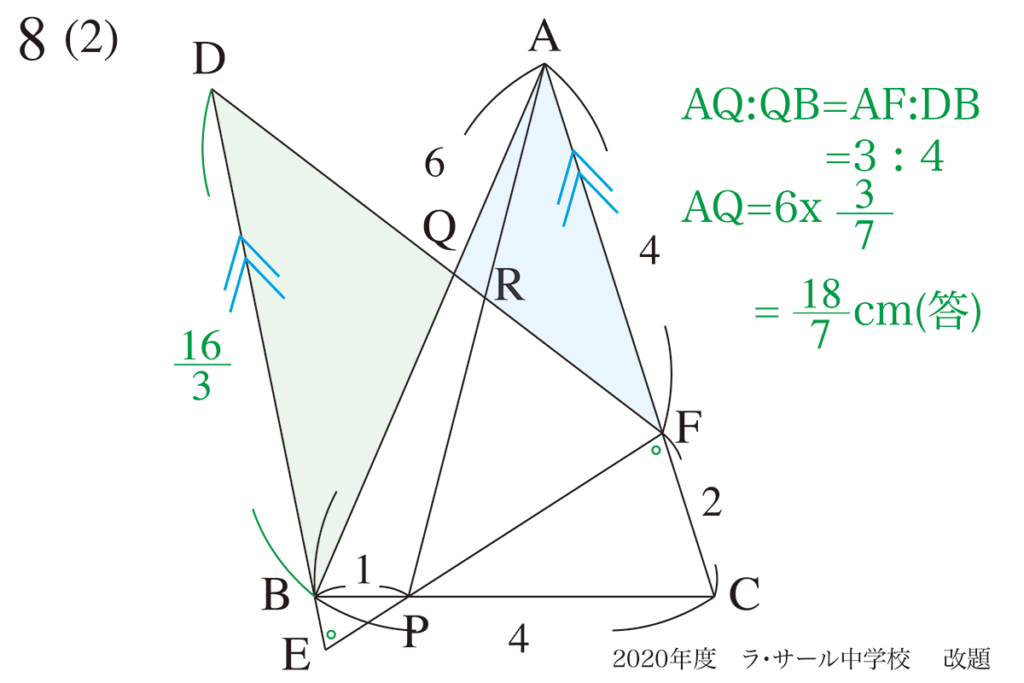
(2)までで移動・回転した二つの図形の状況が、だいぶ分かりました。
・回転した図形も、元の図形も「同じ図形」であることを強く認識
・「同じ辺の長さ」と「同じ角度」を図形に描きこむ
・たくさんの「同じ角度」から、相似形を見つけて相似比を考える
最も大事な性質は、「辺ACと辺DEが平行」であることです。
・直線が互いに交わらない
・直線が互いに「全く同じ向き」を向いている
図形問題で最も大事なことは「平行な辺・直線を見つける」姿勢です。
・平行な直線同士の錯角は同じ
・錯角が同じ直線同士は平行
(3)以降は求める対象が、辺の長さから面積に変わります。
いくつかの考え方があります。
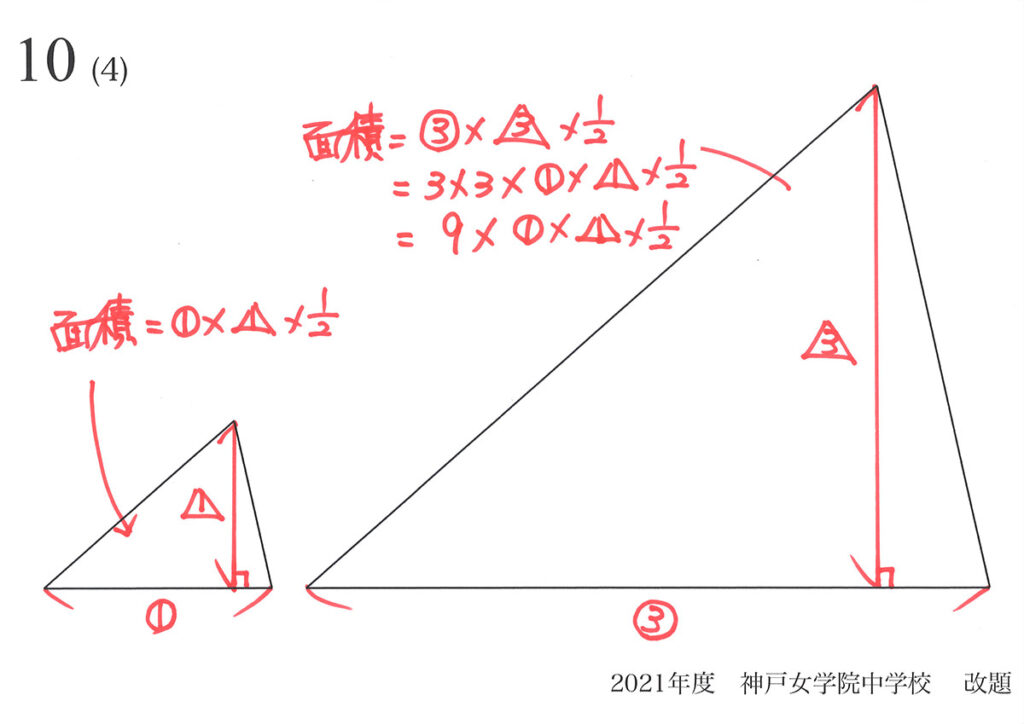
相似図形の面積比は、「辺の比」を2回掛ける（2乗）と計算できます。
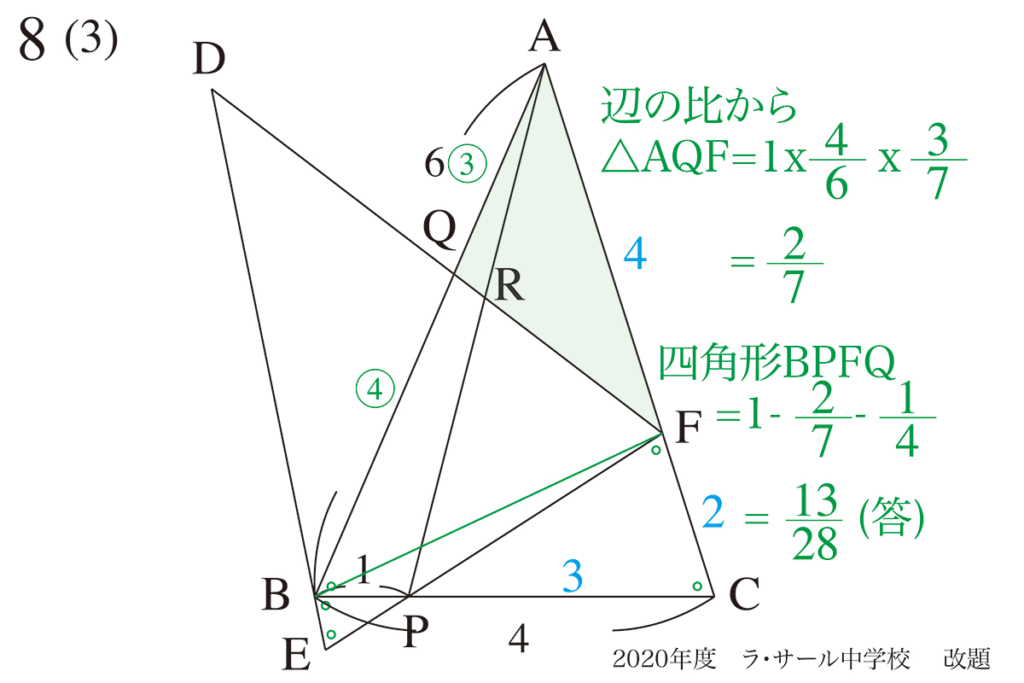
△ABCと△PFCの相似関係を、利用しましょう。
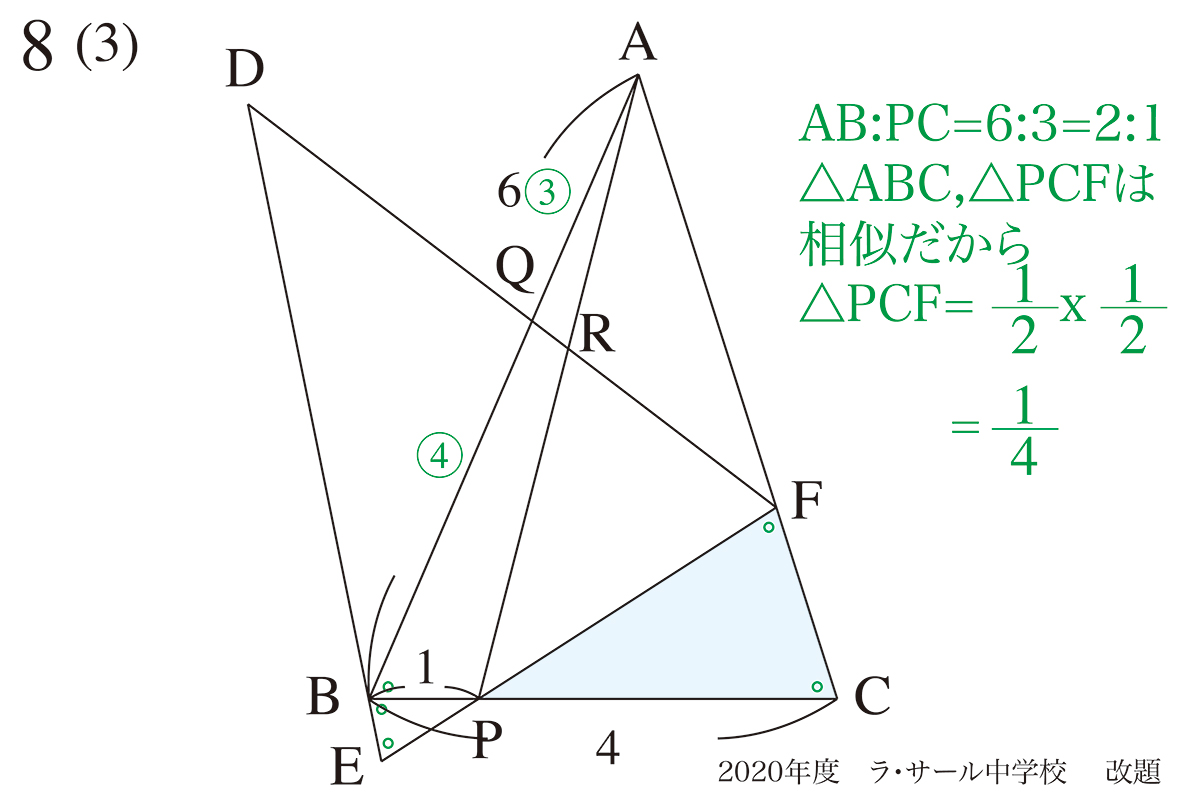
四角形BPFQの面積を考えるには、いくつか考え方があります。
今回は、「△ABCから△PCFと△AQFの面積を引く」で考えましょう。
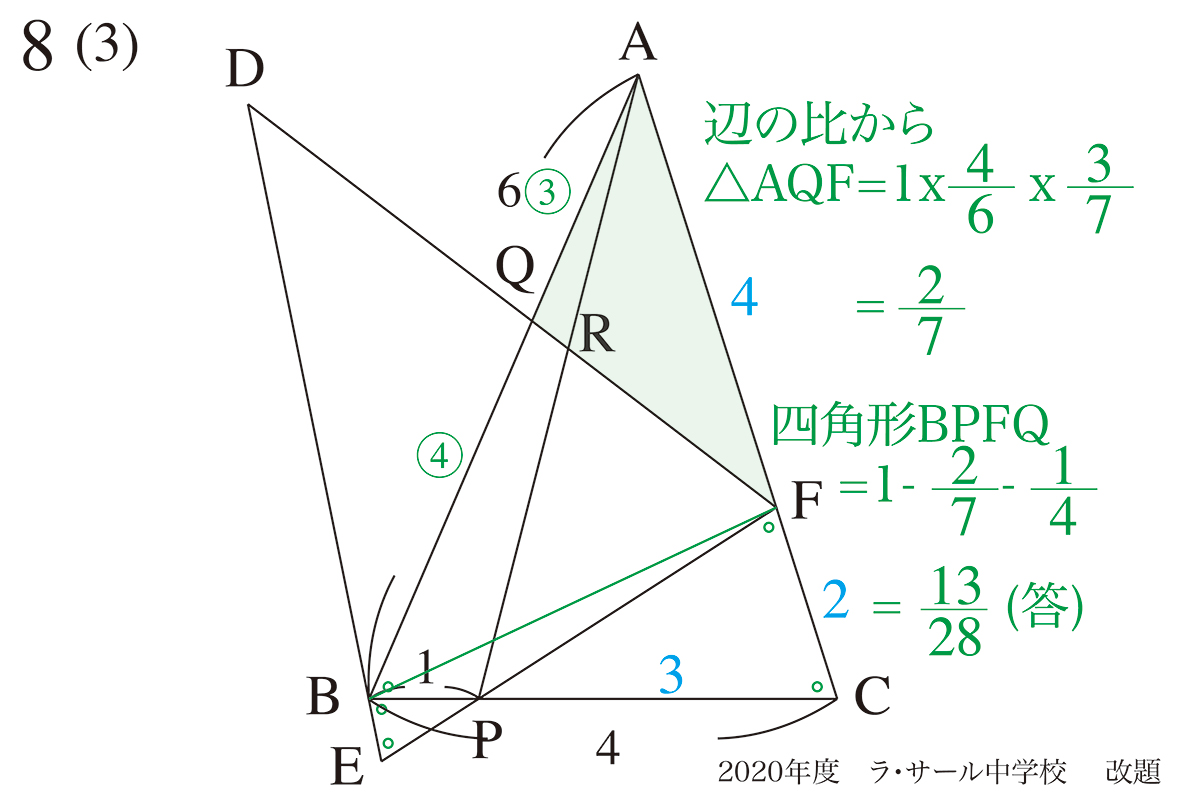
(1)(2)で求めた比を使えば、比較的簡単に求まりました。
男子小学生やっぱり、前の
問題で考えたこと・結果って大事なんだね！
女子小学生問題解いていると、
その問題ばかり気になるけど・・・
女子小学生小問に分かれている時は、
前の問題を気にしよう！
・前の問題が後の問題のヒント・鍵になっていることが多い
・「前で考えたこと・解いた結果」は常に意識
多角的に考える姿勢：違う考え方で解く
図形問題は、たくさんの考え方・解放があります。
今回のように「面積を求める」場合は、「どの図形から、どの図形を引くか」など考えられます。
難関校以上の中学校志望者の方は、図形問題は解法を自分でも考えてみましょう。
男子小学生自分で
考えるの・・・
男子小学生それは、
ちょっと難しいよ・・・
難しく考えすぎずに、
男子小学生こう補助線引いたら、
上手くゆくかな？
色々とトライして、考えてみましょう。
男子小学生あれ？
うまくゆかない・・・
このように「うまくいかない」と気づいた時、それもまた勉強です。
今回は△ABCから二つの三角形を引いて、四角形BPFQの面積を求めました。
△DEFは△ABCと同じです。
女子小学生△DEFは△ABCを回転させたから、
同じね！
そこで、四角形BPFQの面積は、△DEFから△DBEと△PBEの面積を引いても求められます。
色々と考えてみましょう。
女子小学生違う方向から、
面積を求められるのかな？
図形問題は「自分でも別の解き方を考えてみる」ことは、とても良い学びになります。
そして、図形問題が多角的に考えられるようになります。
女子小学生こうしたら、
出来ないかな？
自分で色々考えてみると良いでしょう。
答えが同じになれば、
女子小学生あっ、
出来た！
自分の力で、解き方を考えられると嬉しくなります。
算数・数学では「答えが同じ」=「考え方・解き方が正しい」ことでないことがあります。
「答えがたまたま同じだけ」という可能性もあります。
男子小学生「たまたま同じ」になることが
あるの？
「たまたま同じ」は「ほとんどない」ですが、そういうこともあります。
図形問題においては、「答えが同じ」であれば「考え方も正しい」ことがほとんどです。
男子小学生あっ、違う考え方で解いたら、
答え一緒だった！
男子小学生なんか嬉しいし、図形問題が
得意になった気がする！
すると、図形問題を考えることが好きになるでしょう。
やや難しいですが、図形問題のいい仕上げになります。
少し考えてみて上手く行かなかったら、上記の解法（リンク）を参考にしてください。
(4)解法は次回ご紹介します。
次回は下記リンクです。
