前回は「回転移動する図形の基本・ポイント・コツ〜「同じ辺」と「同じ角度」に注目・図形に「分かること」を描いて「大事な性質」を理解・図形問題は「平行」な辺がポイント・問題 8(1)解法〜」の話でした。
問題 8(再掲載)

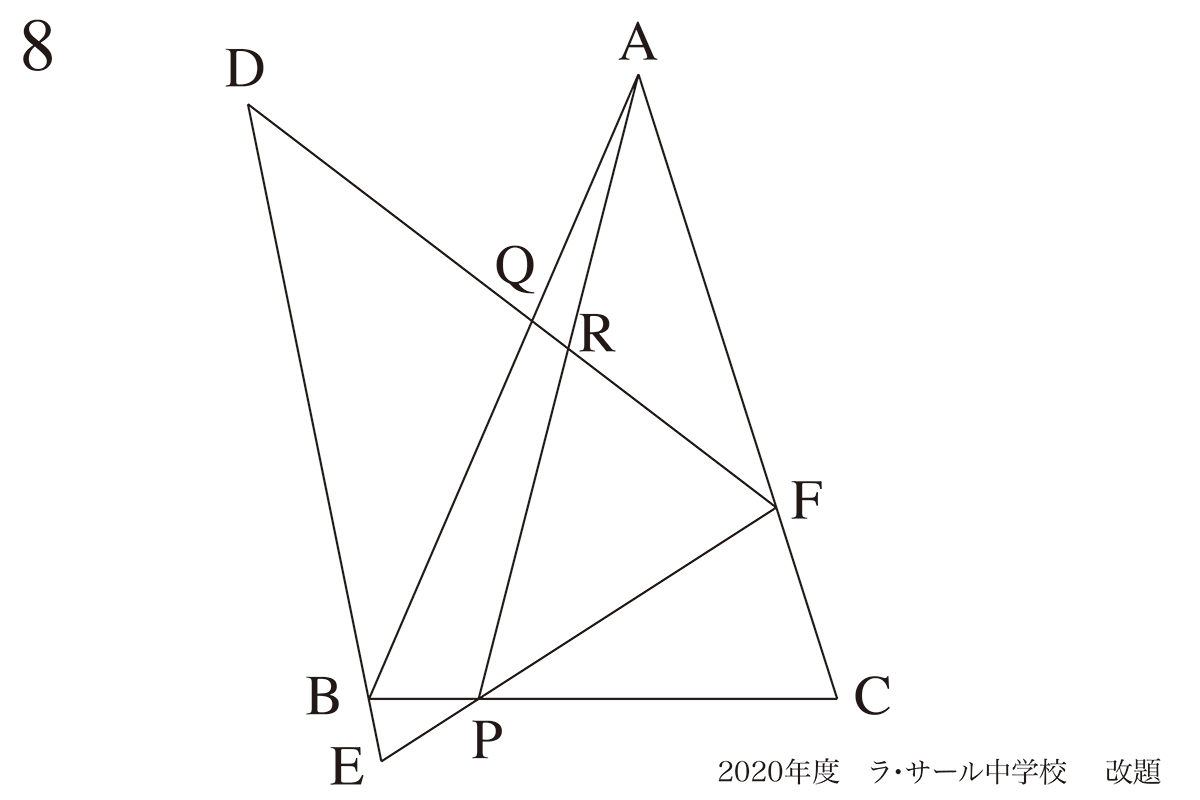
いつも平行な辺を探す姿勢:「平行な辺」と相似図形
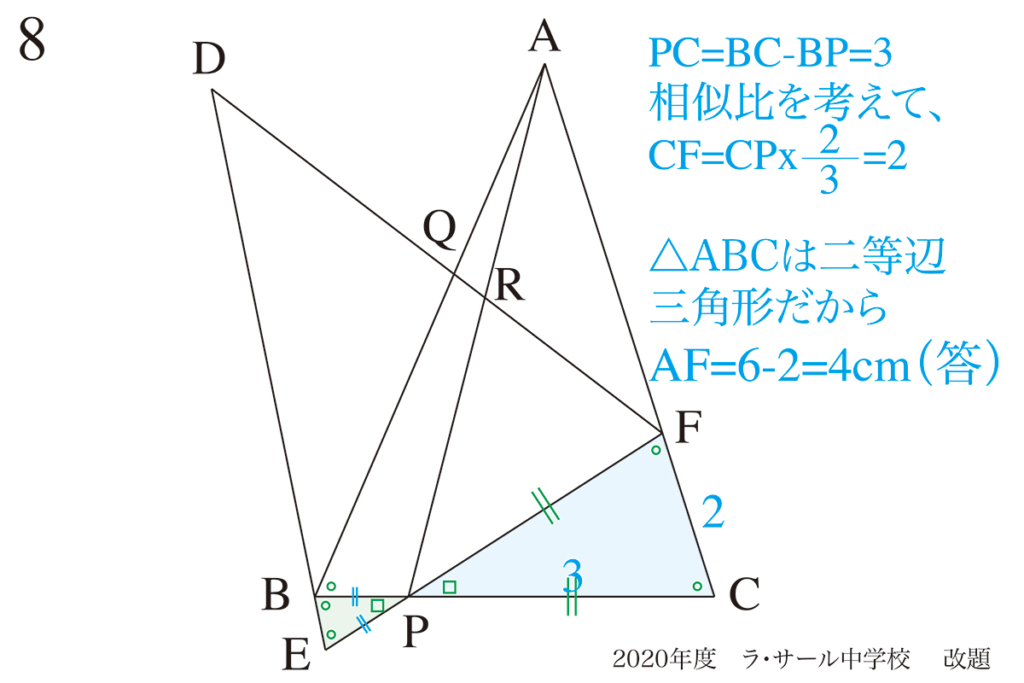
今回は(2)の解法です。
最初は「三角形を回転して重ねた」状況だった二つの三角形。
「同じ角度」を具体的に図形に描きこみ、大事な性質が分かってきました。
・回転した図形も、元の図形も「同じ図形」であることを強く認識
・「同じ辺の長さ」と「同じ角度」を図形に描きこむ
・たくさんの「同じ角度」から、相似形を見つけて相似比を考える
図形問題を解く際には、「いつも平行な辺を探す」姿勢が良いでしょう。
「平行な辺」は、「辺同士がお友達」です。
そして、「平行な辺を見つける」と図形問題を解く鍵となることが多いです。
 男子小学生
男子小学生平行な辺は
どこかな・・・
平行な辺を探してみましょう。



う〜ん・・・
どこかな?
難しく考えすぎないで、「平行」の大事な性質は「同じ方向」です。
・直線が互いに交わらない
・直線が互いに「全く同じ向き」を向いている
「同じ向き」をした辺を探しましょう。



あっ、
ひょっとして!
DEとACが平行です。
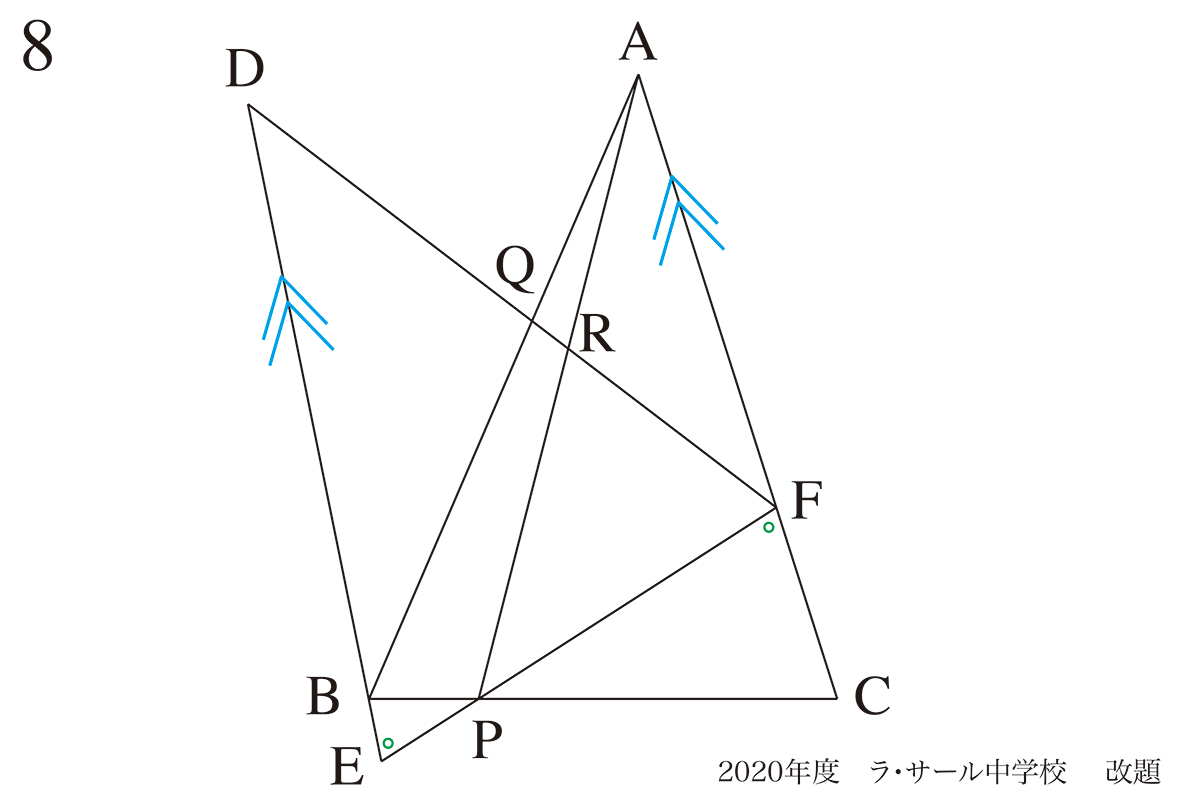

辺EFに対して、角CFP=角BEPなので「DEとACが平行」です。
・平行な直線同士の錯角は同じ
・錯角が同じ直線同士は平行
平行な変が分かれば、相似図形が次々に見えてきます。


△AQFと△BQDは、相似図形です。
平行な辺に対して、直線がクロスするようにあると、同一の錯角・対頂角により相似形が出てきます。



何だか、
これで解けそうな気がしてきた・・・
新たに「平行な辺の組みを見つけた」ら、「解けそうだ」と思うことも大事です。
AQは比を考えれば、求まりそうです。
そのために、DBの長さを出したいのです。
前の問題で考えたことや結果をヒントに:相似から辺の比を考える
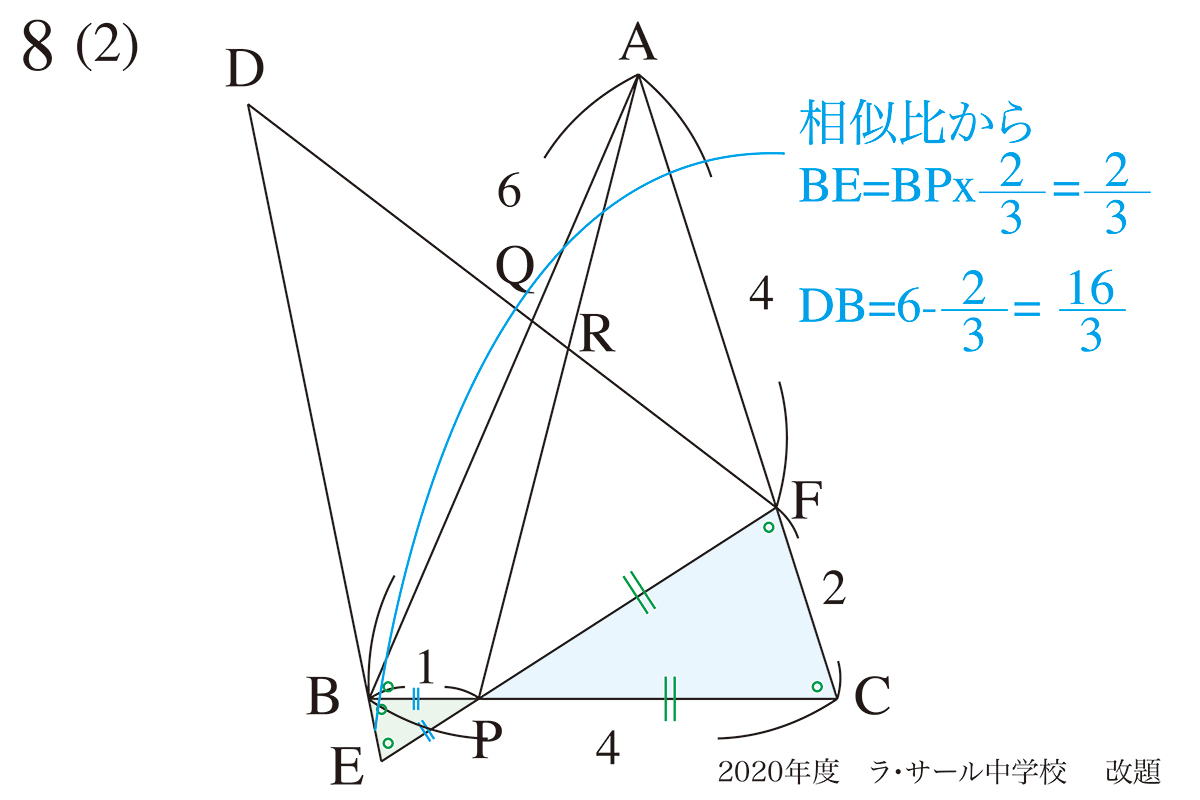

(1)でわかった相似図形を考えて、BEを求めましょう。



ここで、(1)で分かったことが
使えるのね!
文章題などでは、「前で考えたこと・解いた結果」は常に意識しましょう。
小問に分かれている問題は、大抵の場合「前の問題が後の問題のヒント」になっています。
・前の問題が後の問題のヒント・鍵になっていることが多い
・「前で考えたこと・解いた結果」は常に意識
DB=DE-BEですから、DBが求まります。
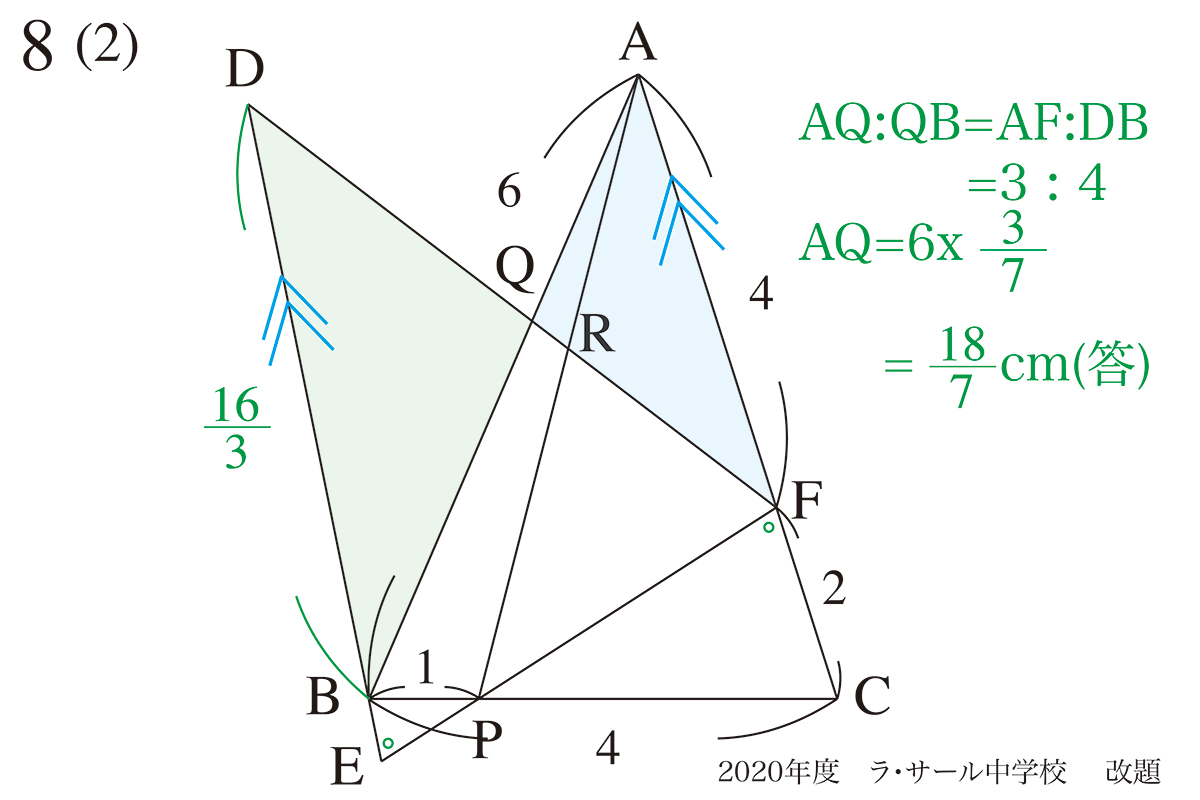

そして、△AQFと△BQDの相似関係から、比を考えると上のようにAQは求まります。
「平行」は非常に大事な性質で、とても役に立ちます。
図形問題では、



平行な辺が
あるか作る!
「平行な辺を見つけるか作る」ことを目指しましょう。
「平行な辺が登場しない平面図形問題」もありますが、比較的少ないです。
大抵の平面図形問題には、「平行な辺がある」か「平行な辺を作る」がポイントになります。
(3)は三角形の面積比を、辺の比から着実に求めてゆきましょう。
(3)解法は次回ご紹介します。
次回は下記リンクです。


