前回は「回転移動する図形が得意になる考え方〜面積比・相似比を2回掛ける・2乗・多角的に考える姿勢・違う考え方で解く・辺の比をしっかり考える・問題 8(3)解法〜」の話でした。
問題 8（再掲載）
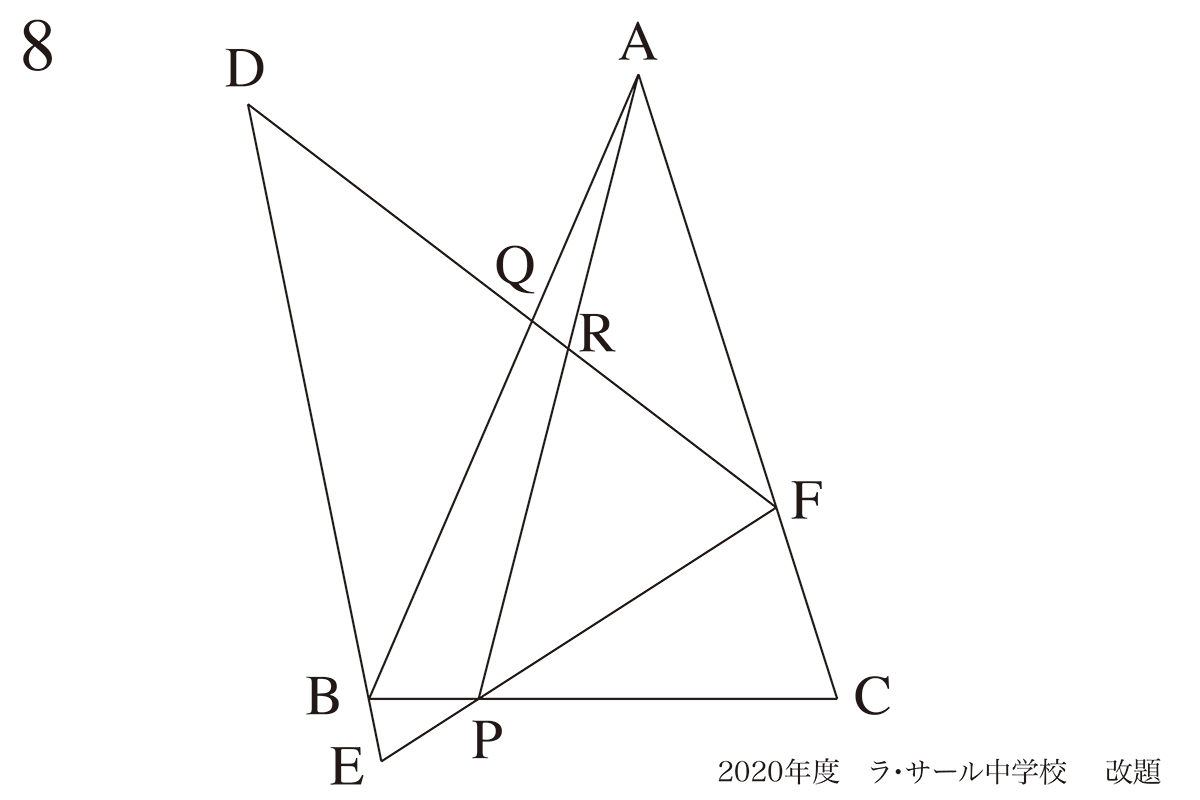
まずは分かったことを整理
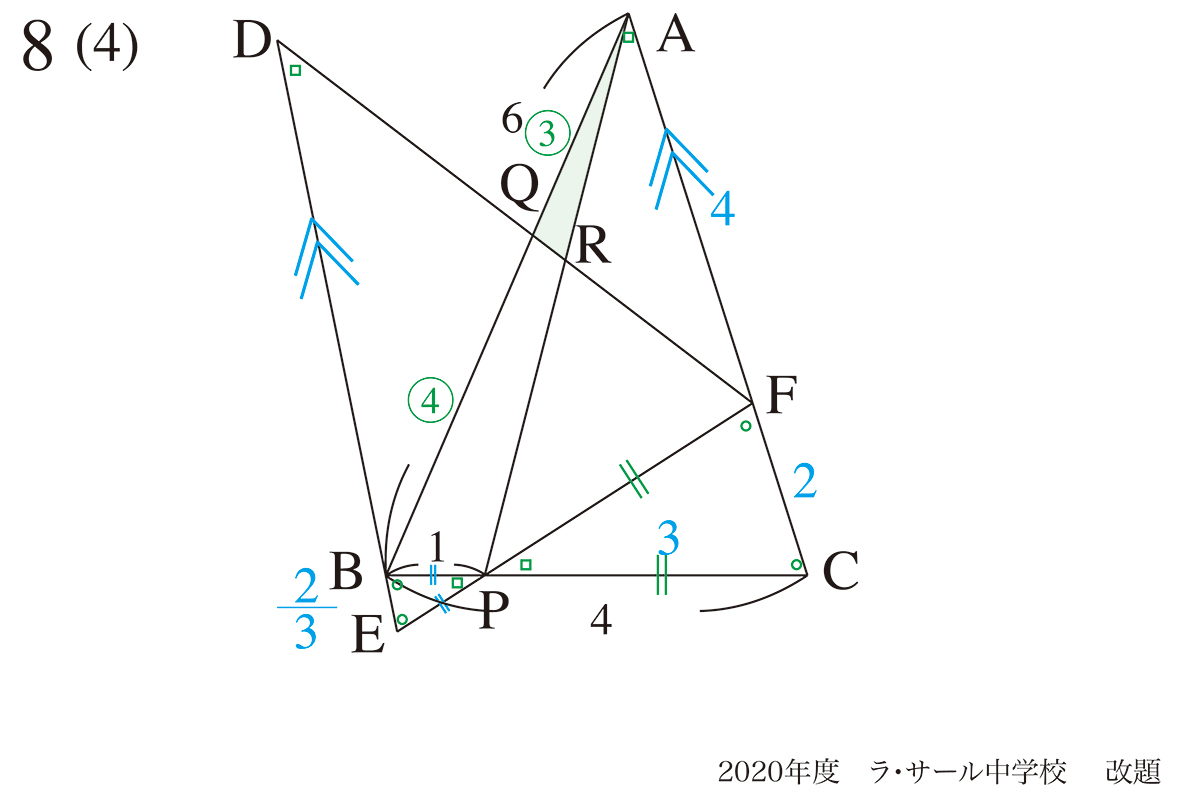
今回は(4)の解法Aです。
まずは(3)まで分かったことを整理してみましょう。
複数の小問がある時は、前の問題がヒントになっていることが多いです。
・前の問題が後の問題のヒント・鍵になっていることが多い
・「前で考えたこと・解いた結果」は常に意識
△AQRを求めるには辺QRと辺RFの比が分かれば良さそうです。
こういう時は「まずは平行の辺に着目して、相似三角形を見つける」です。
男子小学生今まで考えた相似形以外に
相似形はないんじゃない？
見つからない時は、「平行の辺に着目して、相似三角形を自分で作る」のがポイントです。
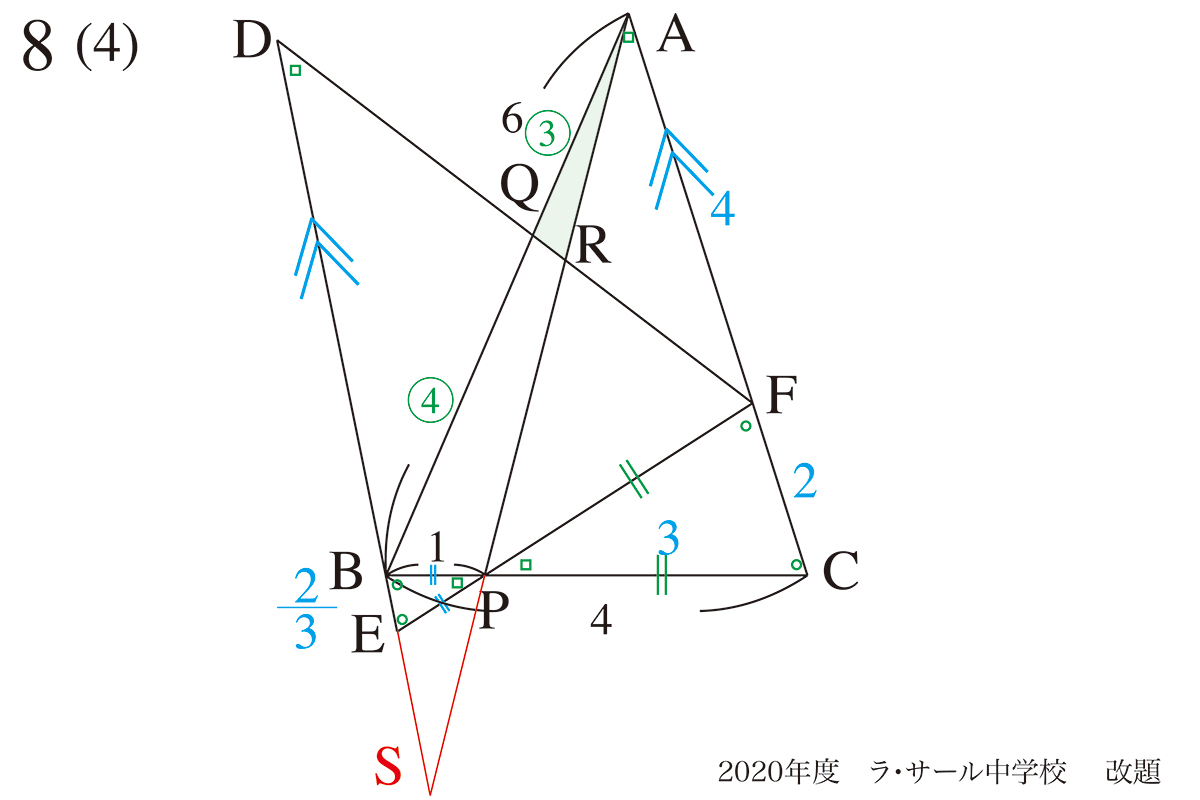
辺APと辺DEを延長した線の交点をSとして、与えられた図形の外に出て行ってみましょう。
女子小学生これなら、新しく
相似形が見つかる！
図形の外に線を延長：外の世界に出る発想
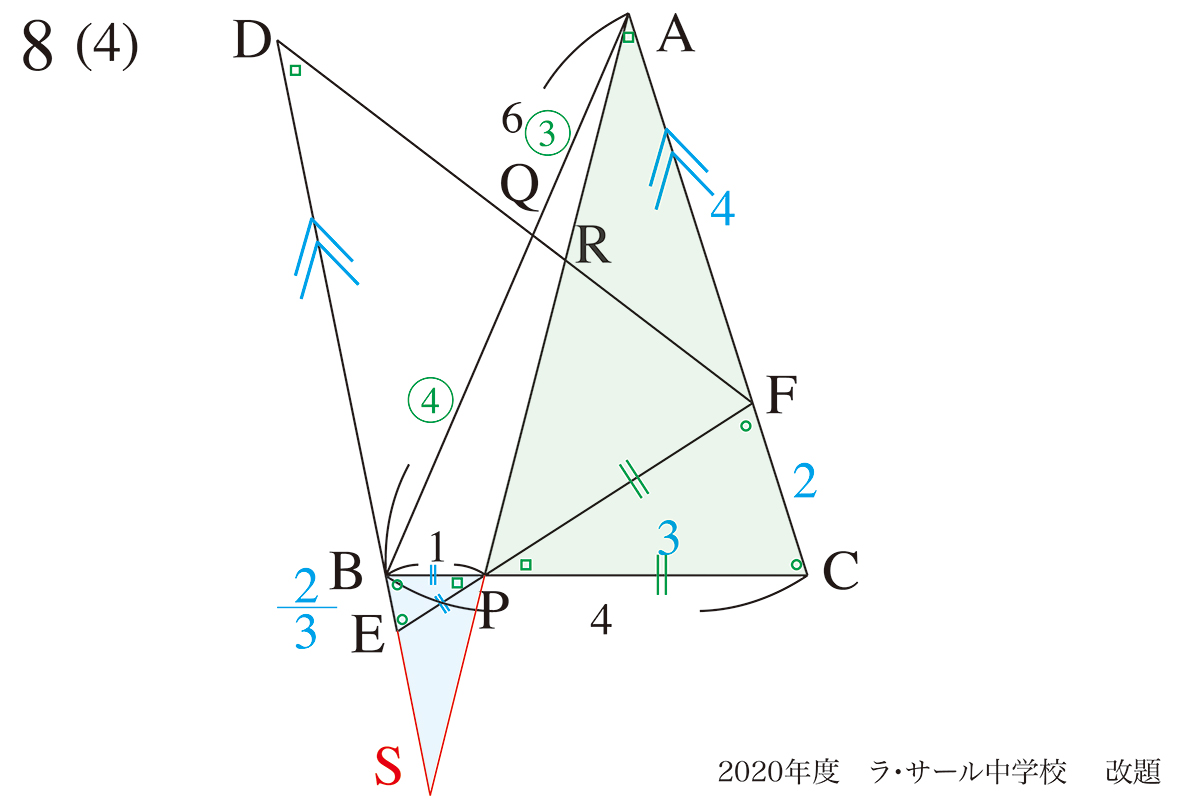
平行な辺があると、たくさんの相似三角形が見えてきます。
△APCと△SPBが相似三角形です。
平行な線があったら、それを利用して線を延長してみましょう。
辺や線を延長して「自分で世界を広げると、見えてなかったコトが見えてくる」ことがあります。
・平行な直線のうち、一つまたは二つの直線を延長する
・平行ではない直線を延長して、新たな交点を作ると相似形が出てくる
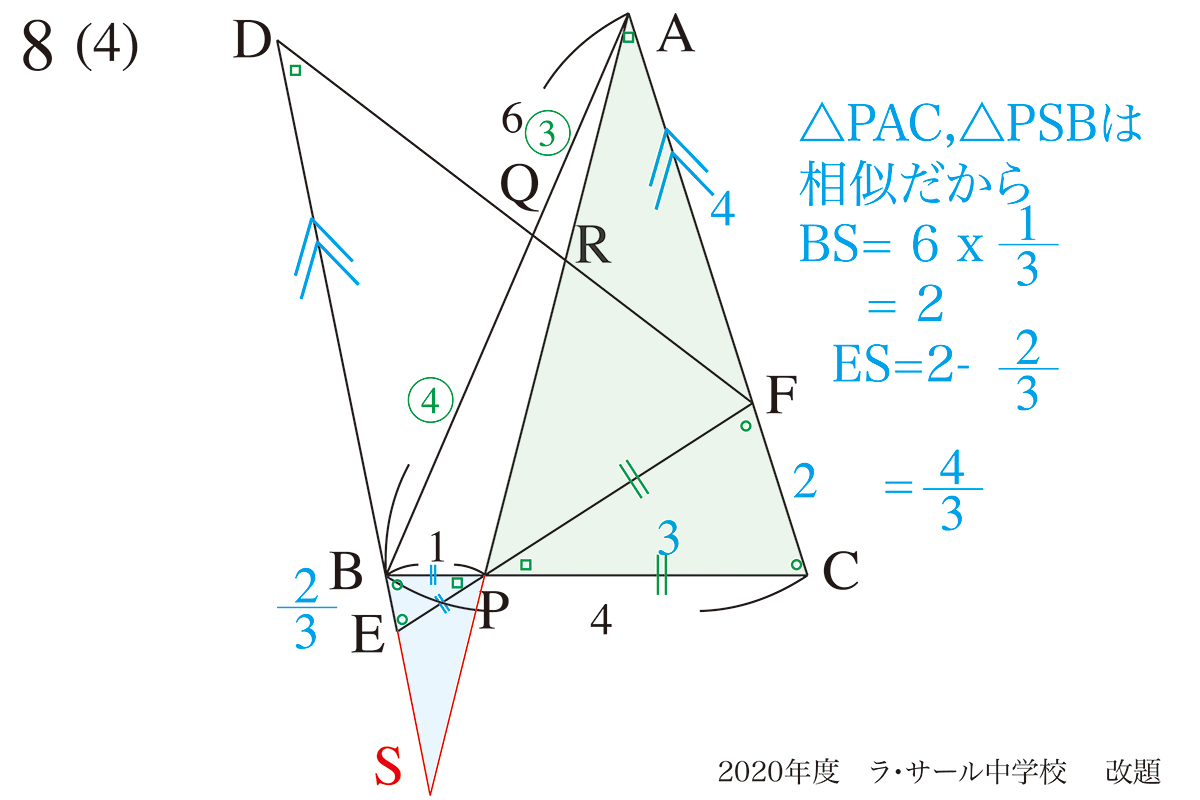
相似関係を利用して、BS、ESの長さが計算できます。
もう一つの相似三角形を見つけたいですが、探してみましょう。
男子小学生そうだね、
ちょっと探してみよう・・・
相似形は「近くに他の相似形のペアがある」ことが多いです。
男子小学生あっ！
△RAFと△RSDが相似だ！
分析するように少しずつ解明：「謎解き」のように楽しい感覚
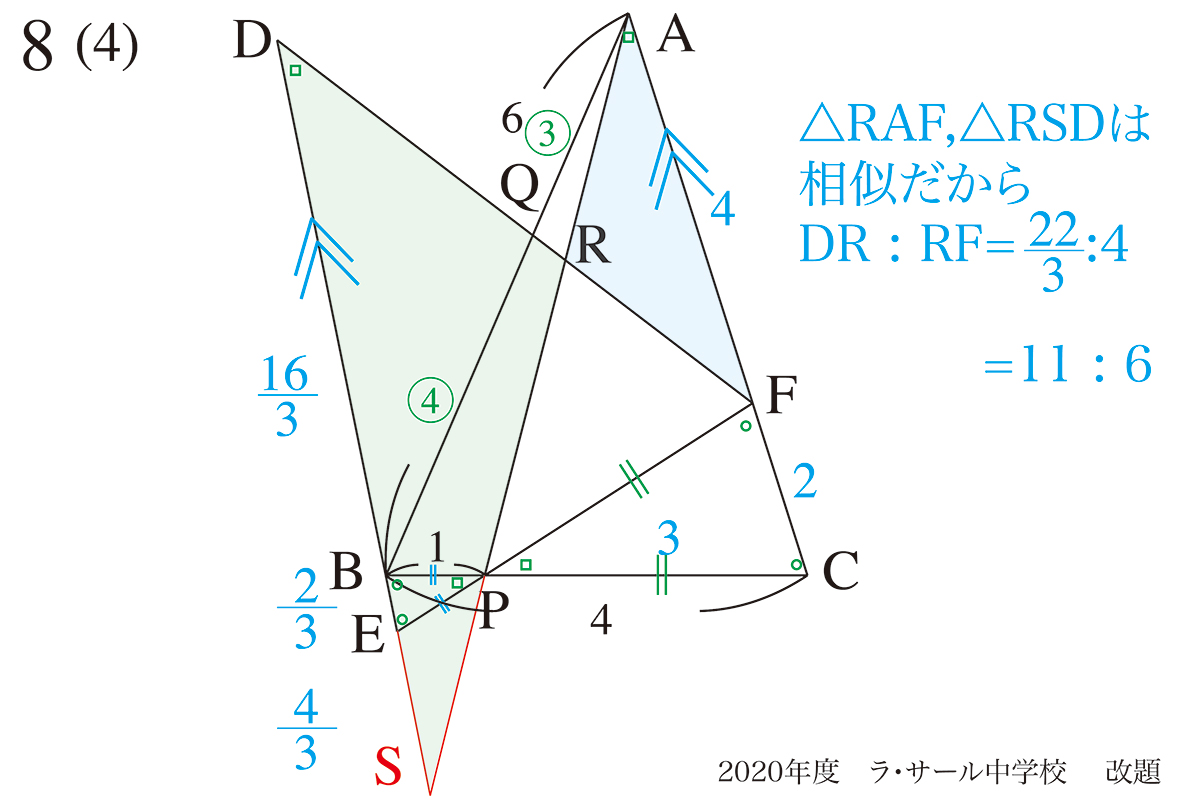
これで、DR : RFの比が分かりました。
女子小学生少しずつ分かってくると、
楽しい！
図形問題は「分析するような視線で、少しずつ解明する」のが良いでしょう。
すると「謎解き」みたいな感じで、楽しく考えられるでしょう。
女子小学生確かに、謎解きみたいに、
「分かる」のが楽しいかも！
あとは、(2)で分かったAQ:QB=FQ:QDを考えて、線分DFにおける辺の比を考えましょう。
DR : RF=11 : 6（11+6=17)
DQ : QF=4 : 3（4+3=7)
二つの比が出てきたので、17と7の最小公倍数17×7=119を考えてみましょう。
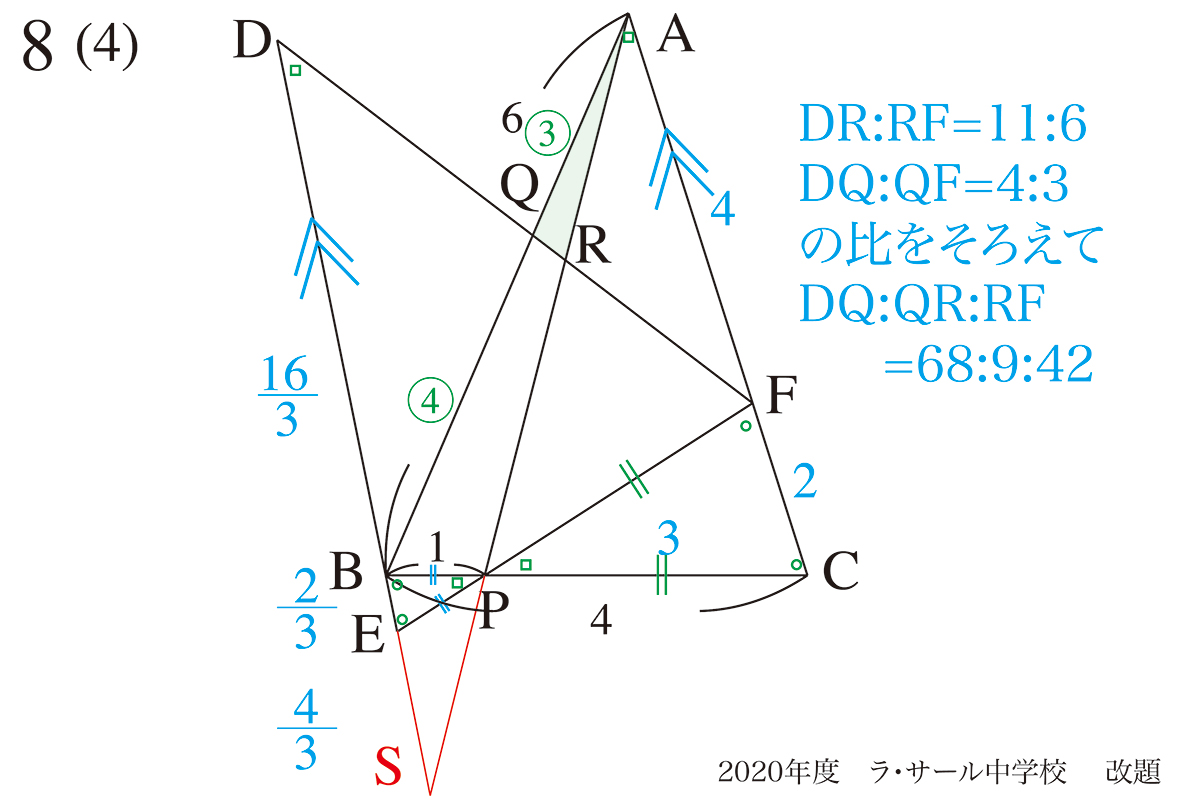
比を整理してみると、上のようになります。
これで、QR:RFが分かったので、△AQRの面積は分かりそうです。
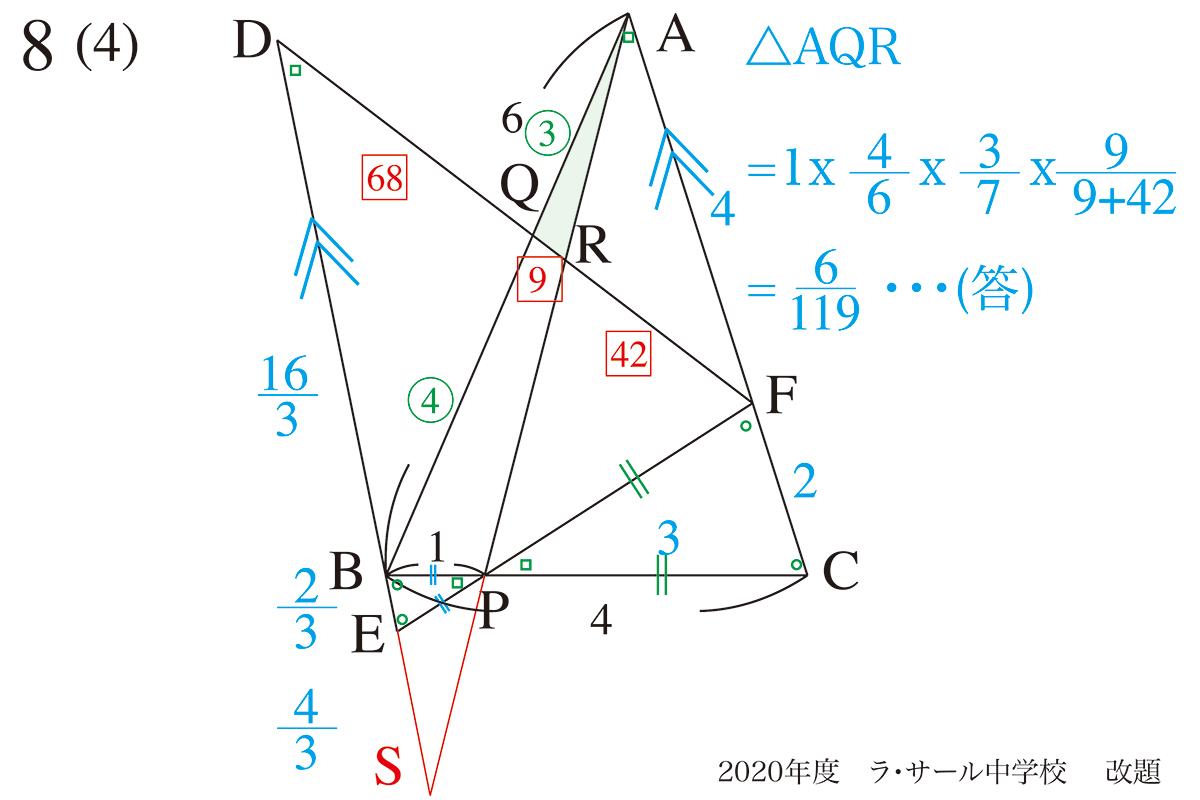
最後の計算で、9+42=51を暗算して、9/51と書いてもいいのです。
9+42は、暗算で
すぐできるよ！
「すぐに計算できる」方も多いと思います。
分数で9+42と書いた方が「きちんと理解している」ことを示すことになります。
また、もし計算ミスで答えを間違えてしまった場合、
採点者いい線行っているけど、
答えが違う・・・
採点者ああ、ここで計算ミスしたのか・・・
きちんと分かっているから、部分点を上げよう・・・
上記のように記載しておく方が「部分点をもらいやすい」です。
記述式では「自分が考えていること」「自分が理解していること」は、明確に表現しましょう。
この解法が最も素直です。
一方で、図形問題は様々な解法があります。
色々と考えてみることは「本質的な学び」になり、「学力が大きくアップする」ことにつながります。
少し異なった視点で、(4)を考えてみましょう。
ヒントは「自分で平行な直線を新たに作ってみる」です。
(4)解法Bは、次回ご紹介します。
次回は下記リンクです。
