前回は「難問が解けるようになる勉強法〜なぜ「動く点を止める」のか・思考の流れを整理・考え方の「引き出し」を整頓・瞬発力鍛える勉強法・大問と小問への対応力アップ〜」の話でした。
算数が得意になる勉強法：手を動かしながら考える
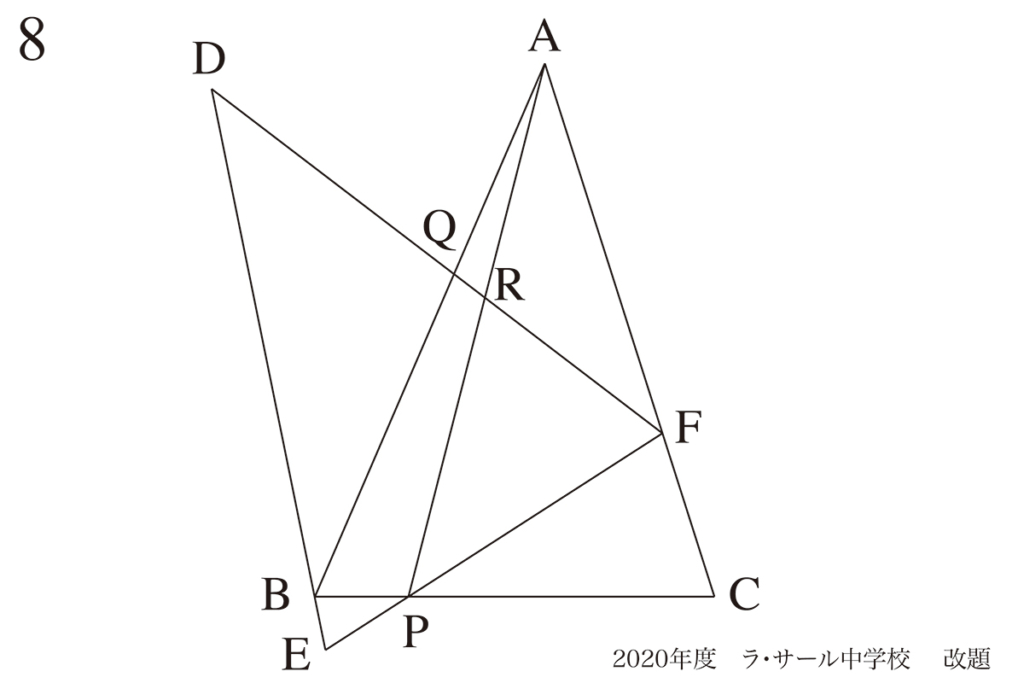
中学受験・高校受験・大学受験の算数・数学において、前段に小問が並ぶ形式の試験の場合。
合格点を確保するためには、これらの小問を見たら前の方の問題に対しては、
男子小学生ああ、
あれだな・・・
こう気づいて、「すぐに手が動く」ことが望ましいです。
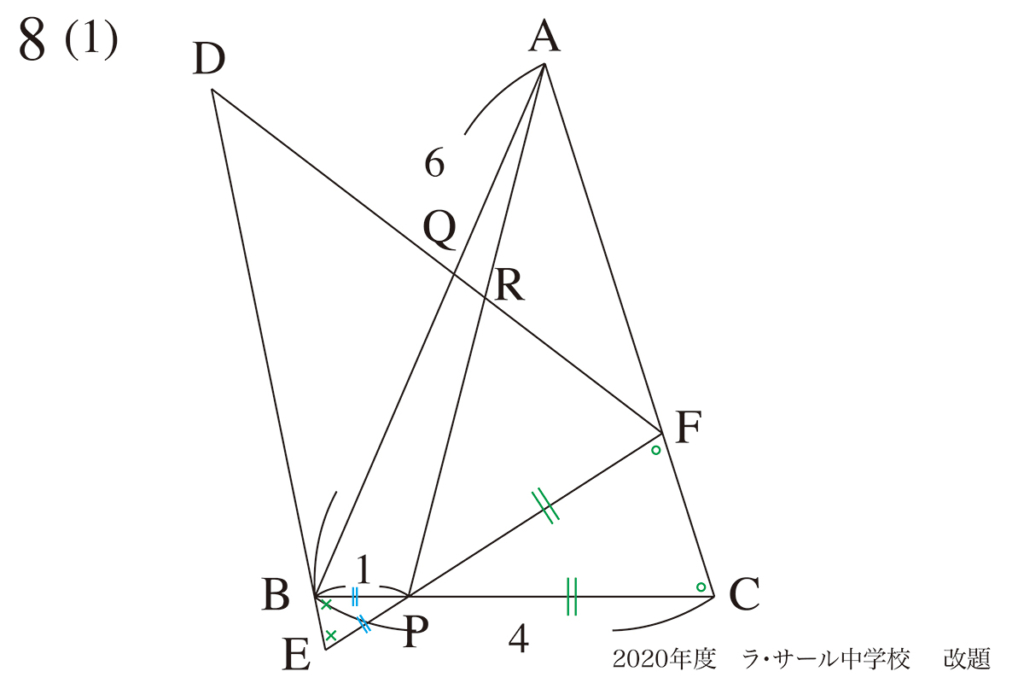
図形問題では正三角形・正方形・二等辺三角形・直角三角形等「特徴のある図形」が登場します。
明確にこれらの「特徴ある図形」が登場しなくても、問題を解いている過程で、
男子小学生あっ、
これは実は二等辺三角形だ・・・
女子小学生この三角形は
正三角形だったんだ！
こう気づくように「特徴的な図形が隠れている」ことが多いです。
・回転した図形も、元の図形も「同じ図形」であることを強く認識
・「同じ辺の長さ」と「同じ角度」を図形に描きこむ
・たくさんの「同じ角度」から、相似形を見つけて相似比を考える
図形問題では「角度や辺の長さが等しい」条件が必ずあります。
逆に、そうした「何かが等しい」等の条件がなければ、問題の作成が難しいです。
出題者この問題では、
ここにポイントの図形があるから・・・
出題者この図形をうまくアレンジして、
問題を作ろう・・・
そこで、「何かが等しい」などの前提条件は図形にどんどん描きこんで、
男子小学生この辺とこの辺の長さが
等しいから・・・
「相似形や合同図形を探す」ようにします。
・直線が互いに交わらない
・直線が互いに「全く同じ向き」を向いている
そして、「平行である辺」を探す、作り出す（補助線）ことがポイントになります。
・平行な直線同士の錯角は同じ
・錯角が同じ直線同士は平行
これら「解く初動ステップ」を強く意識して、どんどん解いてゆくようにしましょう。
そして、この初動ステップで、手を動かしながら考えるようにしましょう。
素早い対応力と問題解決力を育成
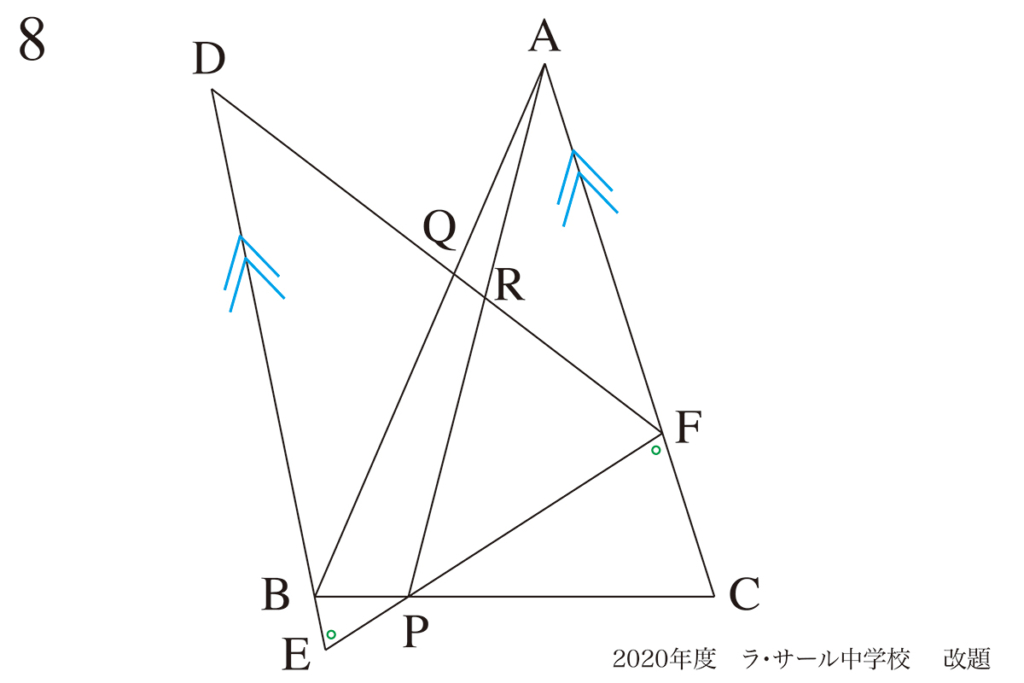
平行な直線が発見できたら、
男子小学生よしっ！
これは解けるぞ！
こう「解ける」と強く思う姿勢も大事です。
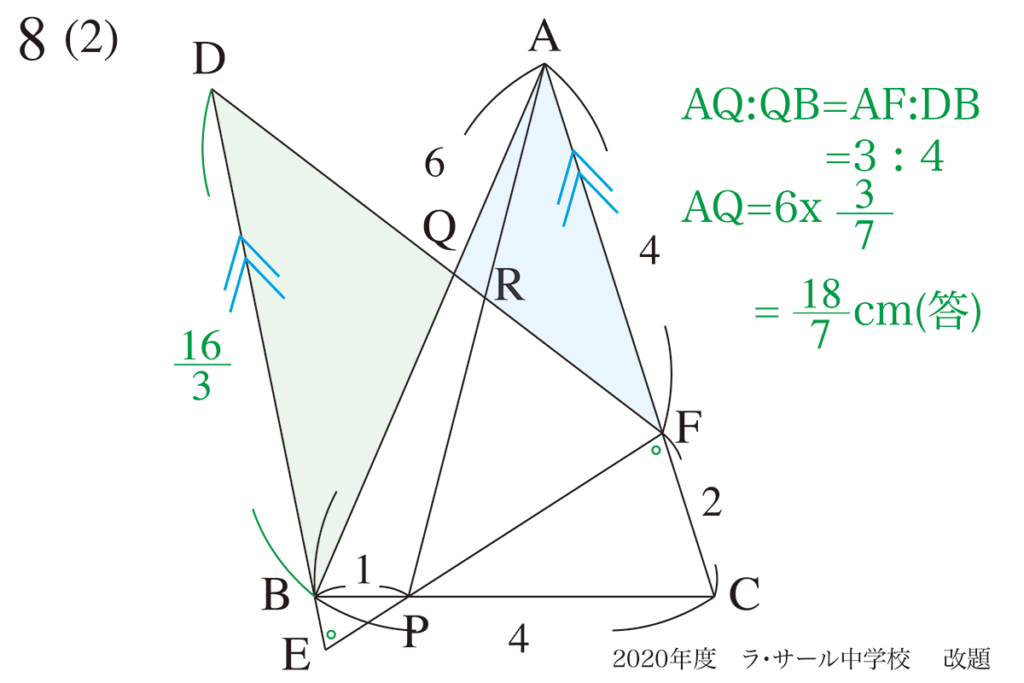
平行な直線が見えたり、作成したら、どんどん手が動いてゆくように学びましょう。
受験期後半〜直前期では、ある程度の目算が立つまで「しっかりと手を動かして考える」姿勢が大事です。
女子小学生これは
どういうことだろう？
女子小学生どこに
着目すれば良いのだろう・・・
こういうことを考えることも大事ですが、その時「手を止めて考える」ことはしないようにしましょう。
「手を動かしながら思考する」姿勢が、難問を解く際には大事です。
難問でも、小問がある時は最初の方の問題はそれほど難しくないことが多いです。
それらの「前段の問題」は、出来るだけ素早くできるようにしましょう。
これは「クイズに早く答えるようになる」ようなことで「本質的な能力」とは関係ないことです。
「学習の習熟度」を測るのは、「何を、どのように学んできたか」という問題が良いです。
一方で「素早い対応力・問題解決力」も入試では大事なので、
女子小学生パッと出来る瞬発力も
大事だね！
そのような問題が出題される形式には、着実に・素早く対応しましょう。
「解法の引き出し」と「解法パターン」：複数の問題が解けるようになる軸
倍数や最小公倍数などが、テーマになりやすい整数の問題。
整数問題の考え方を上記リンクでご紹介しています。
こういう、文章題を考える時、
男子小学生ああ、あれかな？
いや、あれかな？
解法の「とっかかり」が見つからず、
男子小学生よく
分からない・・・
「よく分からない」「解けない」時もあります。
そういう時は、自分で簡単な図形を描いたり、「簡単な具体例」を考えてみましょう。
手を動かして書いて・描いてみると、
男子小学生実は
こういうことかな？
このように「解く鍵」に気付ける可能性が、飛躍的に高くなります。
「分からない」と問題文とにらめっこしていても、なかなか出来るようになりません。（上記リンク）
男子小学生でもさ。
書いたりしてると、時間が過ぎてしまう・・・
女子小学生そう、焦ってしまうことが
多いけど・・・
女子小学生「具体例を考える」良さも分かるけど、
時間がかかって・・・
こういう「自分で具体例を考える」のも「思考の流れを作る」のに役立つのです。
・「こうすれば解ける」ではなく「こうしなかったら、どうなるか」を考える
・なぜ「こうすれば解ける」のか改めて考える
自分で勉強する時は、
男子小学生これは、
どういうことかな？
「なぜこう考えるのか」を意識して考えてみましょう。
ここで、ひたすら、
塾講師解き方はこうです。
この解法を習得しましょう！
「解法を理解すること」に集中していると、「解法のパターン」の習得を重視する学び方になります。
ここで、「思考の引き出し」を整理整頓することを意識すると良いでしょう。
女子小学生そういえば、この間の
あの問題では、こう考えて・・・
女子小学生この問題では、
こういうことに注目して・・・
考え方を整理しながら応用問題や難問に取り組むと、大きく学力が上がります。
「解法の引き出し」を整理すると、
男子小学生この問題は、
あの考え方を使えば良さそう・・・
「どの『解法の引き出し』を使って考えると、問題を解く道筋が見えてくるか」が明確になるでしょう。
・分野ごとに共通する「考え方=思考の軸」を考える
・問題ごとのバリエーションの違いは「同じ」と考えられる思考力育成
この「解法の引き出し」は「解法パターン」と似ていますが、少し異なります。
女子小学生この問題は、
あのパターンだ！
「解法パターン」は、問題ごとに対して解く傾向が強いです。
男子小学生この問題に対しては、
こう考えるのが大事かな・・・
対して、「解法の引き出し」は「問題に対して、どのように考えるか」という思考の軸が詰まった箱です。
・解法パターン：1つ〜2つ程度の問題ごとに対して解くパターン
・解法の引き出し：方向性を明確にして、複数の問題が解けるようになる思考の軸が詰まった箱
「パターン習得が近道」という考え方もありますので、「その方法が良い」ならば良いでしょう。
そういう思考性も、また個性です。
「解法のパターンの習得」ばかりしていると、応用力が育ちにくくなると考えます。
「自分で具体例を考えた上で、解法を学ぶ」と、「考え方の流れ」がしっかりと身に付きます。
「考え方の流れ」が身につくと、応用力・学力が上がり成績も上がるでしょう。
特に応用問題や難問は、多くの問題をこなすよりも「しっかり考える」を実践してみましょう。
すると、算数の学力は大きく上昇するでしょう。
次回は下記リンクです。
