前回は「記述問題に「楽しく取り組む」ポイント〜私立中学のカラーとボーダーラインの合否判断・エッセーや記述が「当たり前」の欧米の受験制度〜」 の話でした。
記述式問題の対策とコツ：出来るだけ「考えていること」を簡潔に書く
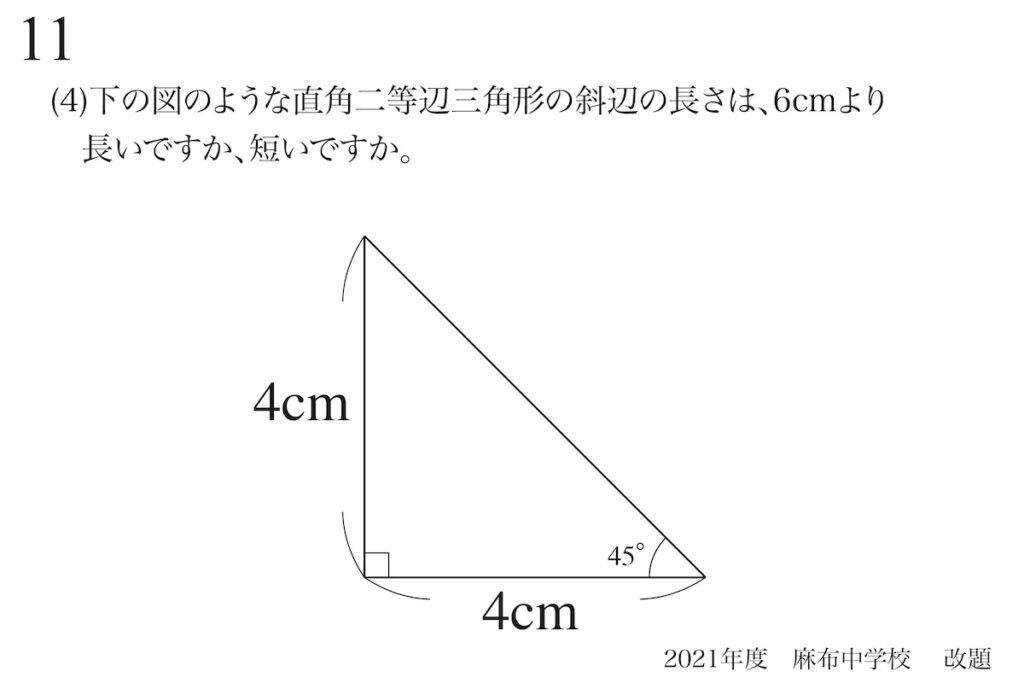
算数実践において、「斜辺の長さと6cmを比較」した問題を考えました。
本問題の考え方は、上記リンクでご紹介しています。
小学生・中学受験生の方で、「ピタゴラスの定理」を知っている方もいらっしゃるでしょう。
基本的には「三角形の斜辺の長さ」は小学校の算数の範囲外ですが、面積の視点から考えてみました。
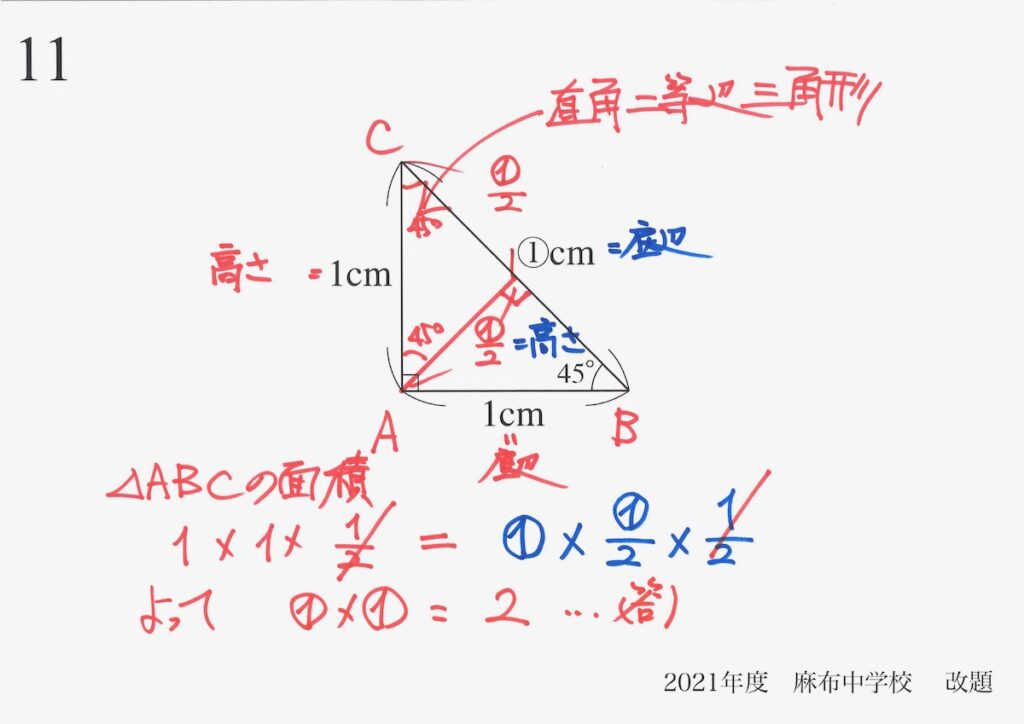
こういう問題は、記述式で出題される可能性があると考えます。
同じ問題の「前の小問」で、上のように「斜辺の長さを2回掛けた数」を考えました。
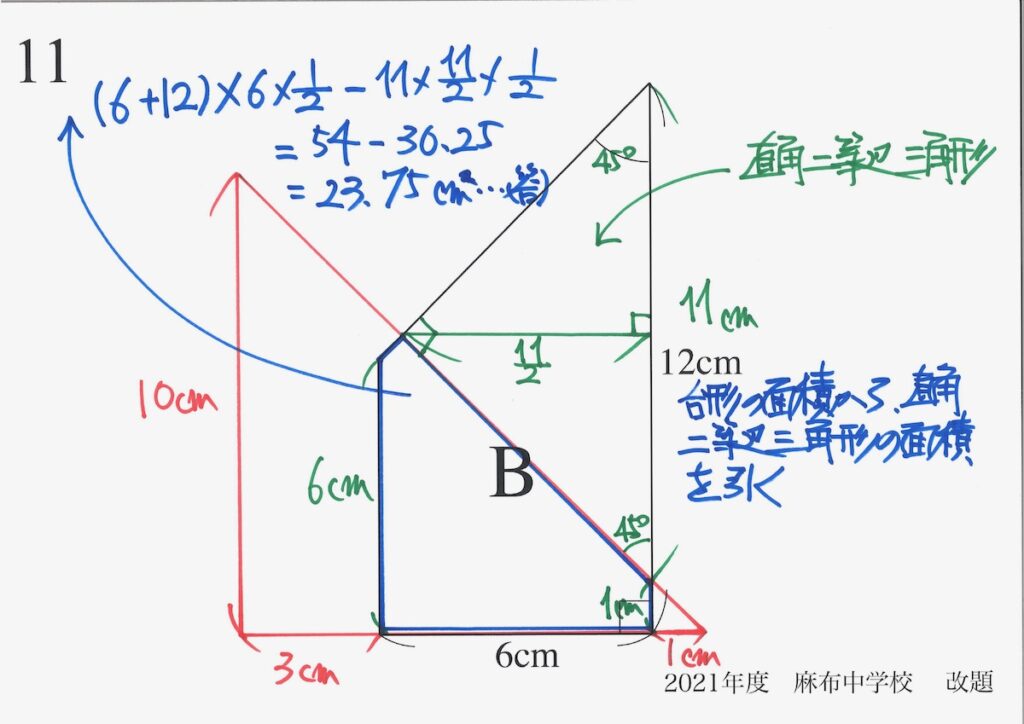
この直角二等辺三角形を「4倍にした時、どうなるか」を考えるのが、本問です。
ここでは、「分からない数を2回掛ける」のがポイントです。
すると「分からない数」が比較できるようになります。
「2回掛けて」→「大小比較して」→「答え」でも良いですが、出来るだけ理由を書きましょう。
上の解答例では「長さを2回掛けた大小と長さの大小は同じだから」と書いています。
男子小学生当たり前だから、
書かなくてもいいんじゃない・・・
女子小学生時間が
もったいないけど・・・
「時間が大事」ですが、記述式ではこういう「理由を明記・表現する」と採点者は、
採点者よく
分かっているね！
この様に好感を持つでしょう。
小学校の算数の範囲では「2回かけた大小」と「その数の大小」は同じです。
実は中学以降の数学では、「2回かけた大小とその数の大小は必ずしも一致しない」のです。
男子小学生え？
なぜ？
これは、算数の範囲を逸脱するので、中学以降の数学でのお楽しみとしてください。
「思考力を判断したい」という記述問題出題者の考え
採点しているのは、中学・高校の数学教師です。
「数学のプロ」から見て、「当たり前ではないこと」には敏感になる傾向があります。
そこで、解答例では「長さを2回かけた」と具体的に書いています。
ここで「長さ」に触れずに「2回かけた・・・」と表現すると、数学的にはバツになってしまいます。
算数としては、この部分は表現しなくても✖️にはならないと考えます。
この意味では、「書かなくてもよいこと」ですが、「書いた方が、論理的」です。
時間が惜しいようでしたら「もっと短く、端的に」でも良いでしょう。
「記述式」の形式にする理由は様々ありますが、
採点者志望者の
思考力を見たい・・・
最も大事なことは「思考力を判断したい」ことです。
記述式を課す学校にとって「丸暗記」ではなく、「考える思考性を持つ」子どもの方が望ましいでしょう。
この「ほんの少し」の配慮で、採点者は、
採点者しっかり
理解している子だ・・・
採点者きちんと
考えているね！
この様に考えるでしょう。
記述問題で思考力を増強
受験生の立場からすると、
男子小学生一点でも多く
点数を上げたい・・・
女子小学生とにかく、あと少し
成績を上げたい・・・
こういう気持ちになる方が多いでしょう。
実際に、「一点差」で当落が起こるのが試験・受験です。
「答えのみ」の問題であれば、「答えがあっているかどうか」のみで採点が判断されます。
そして、記述式問題の出題が多い学校でも「記述のみ」ということは、ありません。
必ず「選択肢を選ぶ」問題や「答えのみ」の問題があるので、
男子小学生記述も大事だけど、
時間制限があるから・・・
この様に焦ってしまう気持ちになります。
一方で、こうしたことを「きちんと表現する」ことは、採点上有利になると考えます。
「時間制限がある」ので、文字が少し雑でも良いでしょう。
「走り書き」でも良いので、どんどん「考える姿勢」を表現しましょう。
このように「記述問題だから書く・描く対策」と同時に、記述問題は思考力の増強につながります。
参考書や問題集の解答を写してみると、
男子小学生これって、
こういうことかな・・・
この様に色々な気づきが生まれることがあります。
こうして思考の流れを記述してみることは、考え方の整理につながります。
「記述対策」だけではなく、「記述してみる」学びは本質的な学力を高めるでしょう。
そして、この「記述してみる」ことは思考力の整理につながり、学力がアップするでしょう。
次回は下記リンクです。
