前回は「ばね・てこのコツ・ポイント 2〜「つり合っている」イメージ・異なる点でのつり合い・「棒の重さ」が「ある」と「ない」・「ない」に仮定して簡単に・他の点でのつり合いを考える〜」の話でした。
棒の重心と中心：「複雑」を「簡単」に考える姿勢
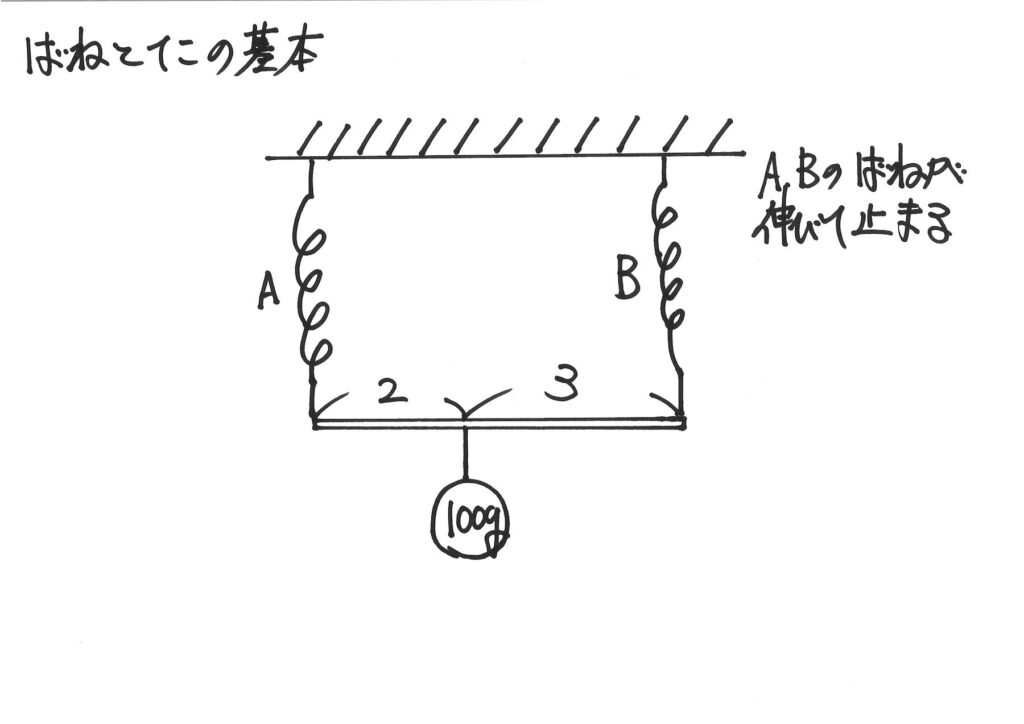
「棒の重さがない」仮定・前提で、上のバネA、Bに「かかる力=引っ張り上げる力」を考えました。
「ある」はずの「棒の重さ」を「ないもの」として考えると、簡単です。
・「ある」ものを「ない」と仮定して考える
←「状況を簡単にして、解けるようにする」ため
考える対象を簡単にして、「分かりやすくする」のが、理科・物理の大事な考え方です。
「複雑なままでも分かる」のが良いですが、それでは「全然わからない」ことが多いです。
そこで、「複雑な状況を簡単にする」ことで、「大事な性質を理解する」ことも大事です。
そして、「複雑」を「簡単」にすることで、「全く分からないこと」の概要がわかるようになります。
算数でも理科でも、バシッと「ピッタリとした答え」が分かれば良いですが、難しい面もあります。
「複雑なモノ・コトを簡単にする」姿勢は、算数・理科では大事です。
・状況を少し簡単にして大事なことを知る
・複雑な状況に対して、簡単なモデルを想定して本質的・大事なことを探す
「棒の太さが同じで、密度も同じ（一様）」であれば、「棒の重さ」を考えるのは難しくありません。
「棒の重さ」が「ある」場合は、「棒の重さが重心に全て集中している」と考えます。
男子小学生重心って、
難しそう・・・
「重心」と言う言葉は、中学〜高校の数学で習いますから、まずは「モノの中心」と考えましょう。
・モノの中心
・モノの重さが集中してかかる場所
例えば、円の重心は中心です。
正三角形、正方形（正四角形）、正六角形などの重心も中心にあります。
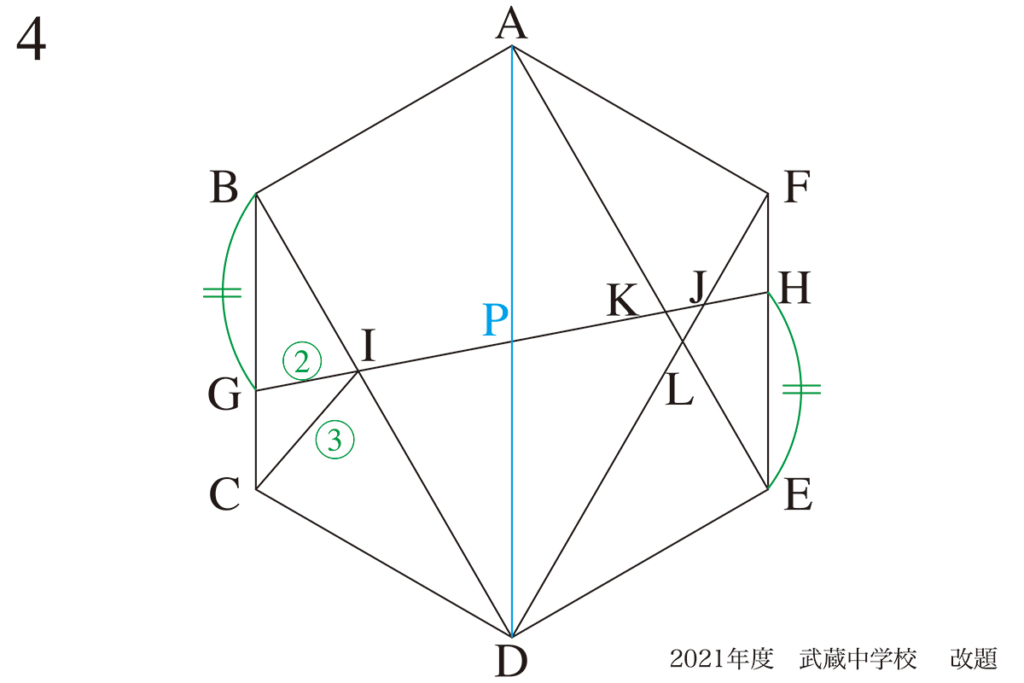
重心・中心は、「モノの中心」なので、非常に大事です。
そして、「重心・中心を考えると、何か大事なことが分かる」可能性が高いです。
図形問題では、中心・重心に注目するようにしましょう。（上記リンク）
中心・重心を通る補助線は、「何か大事なことが分かる補助線」であることが多いです。
・中心=重心から大事なことが分かることが沢山ある
・中心=重心を通る補助線は大事
つり合っている=安定している：色々な点でのつり合い
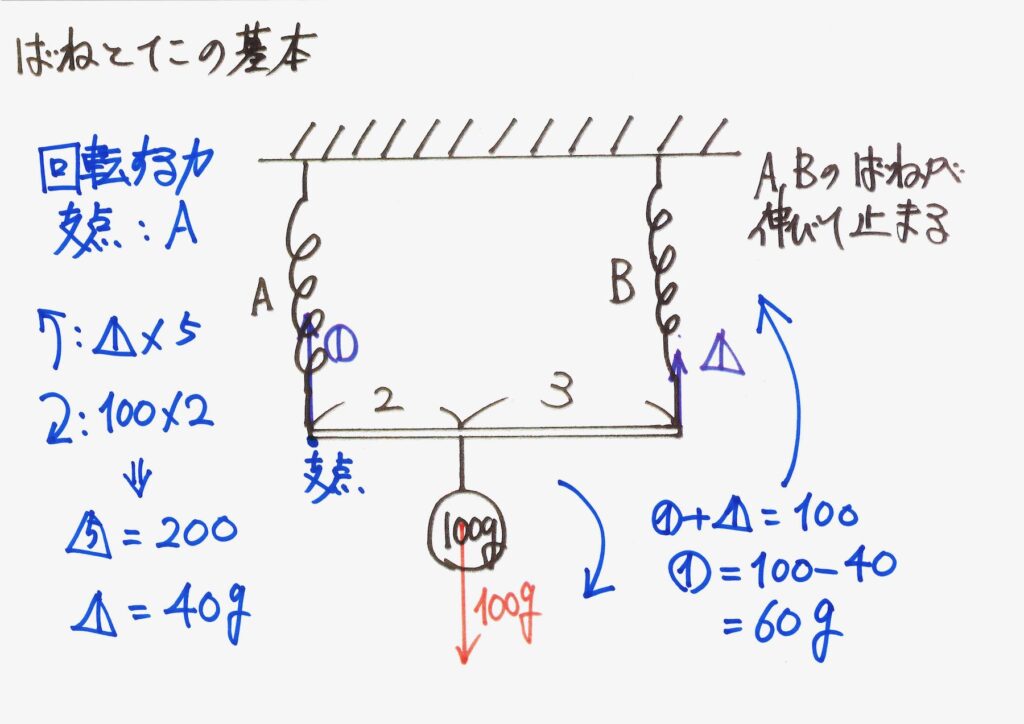
バネAと棒の接点を中心に「モーメント（回転する力）のつり合い」を考えました。
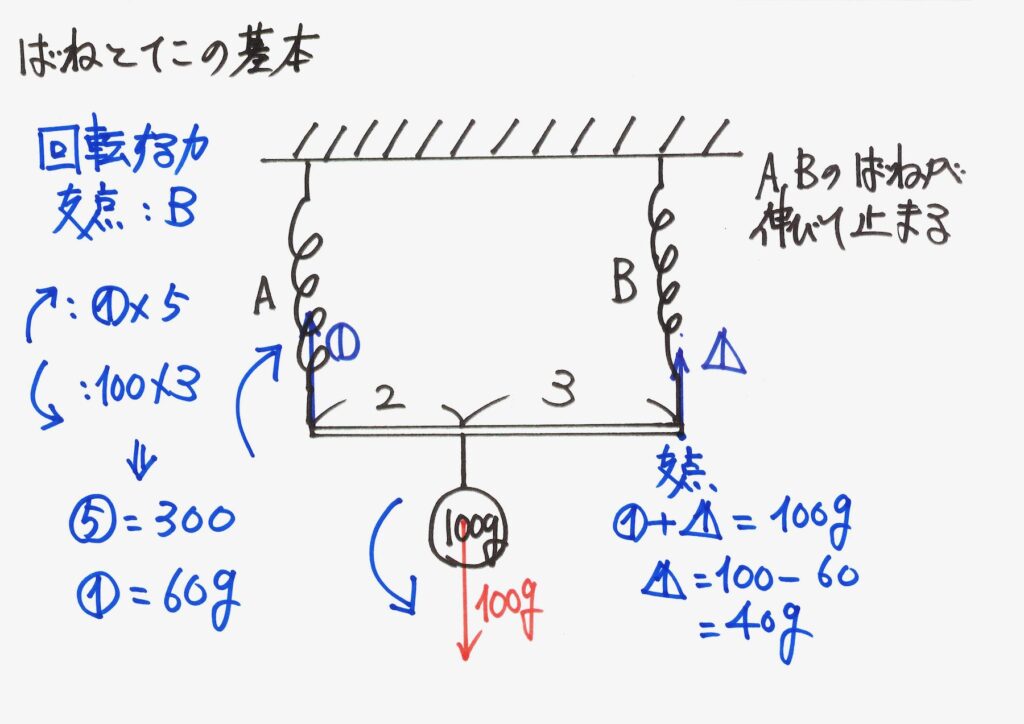
バネBと棒の接点を中心に「モーメント（回転する力）のつり合い」を考えました。
いずれの場合でも、バネA、Bにかかる力を計算することが出来ました。
「棒とバネ全体がつり合っている=安定している」ことは、「棒のどの点でもつり合っている」のです。
・安定（静止）している状態
・棒のどの点でもつり合っている=安定している状態
男子小学生じゃあ、
棒の他の点でも「つり合っている」んだね！
女子小学生他の点でのつり合いを
考えても出来るのかな？
実際に「他の点でのつり合い」を考えましょう。
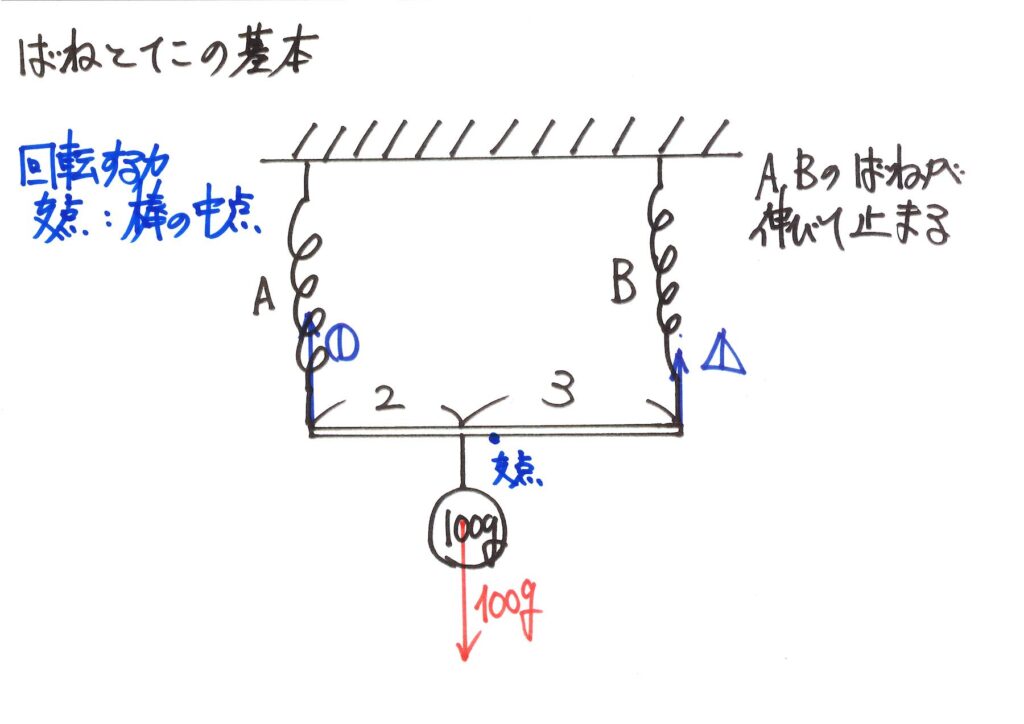
今回は、棒の中点で「回転する力」を考えてみましょう。
男子小学生今回は、棒の中心は
関係ないけど・・・
女子小学生そうだね。
勝手に考えていいのかな？
棒の中心は問題では触れられてなく、「関係ない」です。
棒が釣り合って止まっているので、どの点を考えても「釣り合っている」はずです。
女子小学生確かに、
そうだね。
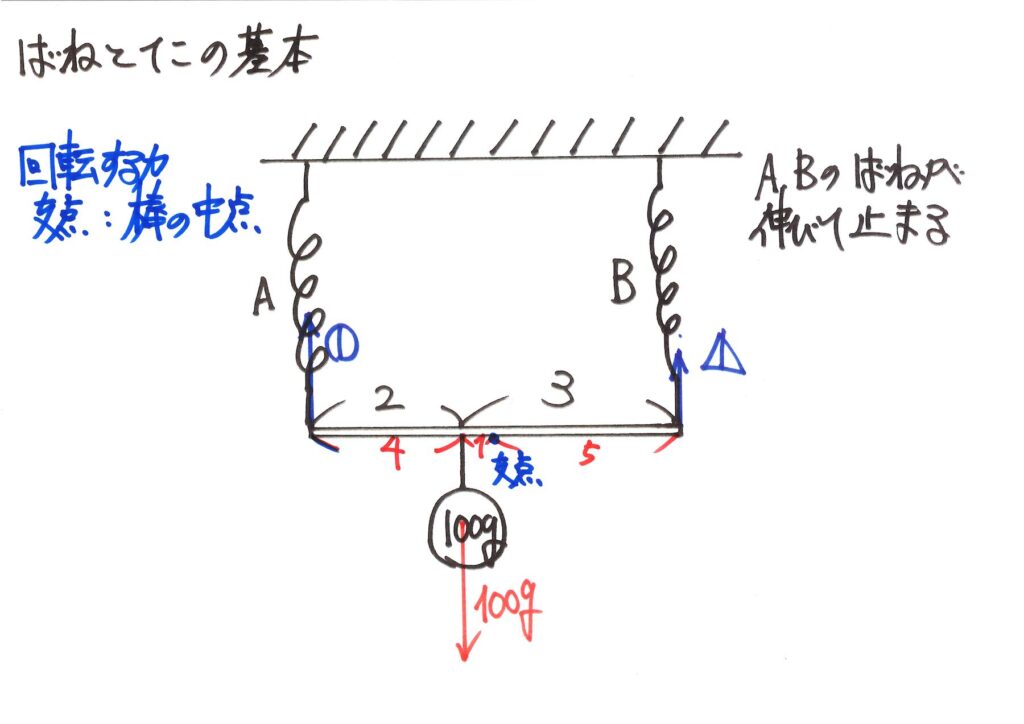
まずは、棒を「2:3」と「1:1（中点）」に分けるので、長さの比を揃えましょう。
「2 : 3」の比の合計5と「1 : 1」の比の合計2の最小公倍数である10で、比を分けます（按分）。
左から、「4 :1 : 5の比」に分かれた部分に、おもり、中点、バネBと棒のつながる点があります。
棒の中心で考えて、「回転する力」を描いてみましょう。
これまでは、2つだった「回転する力」は、3つになりました。
女子小学生考えることが、
増えちゃったね・・・
男子小学生ちょっと
難しそう・・・
食塩水が3つになっても、「2つの場合と同じように考える」で解けます。（上記リンク）
対象が増えても「考えることが同じ」であれば、「出来るはず」なのでやってみましょう。
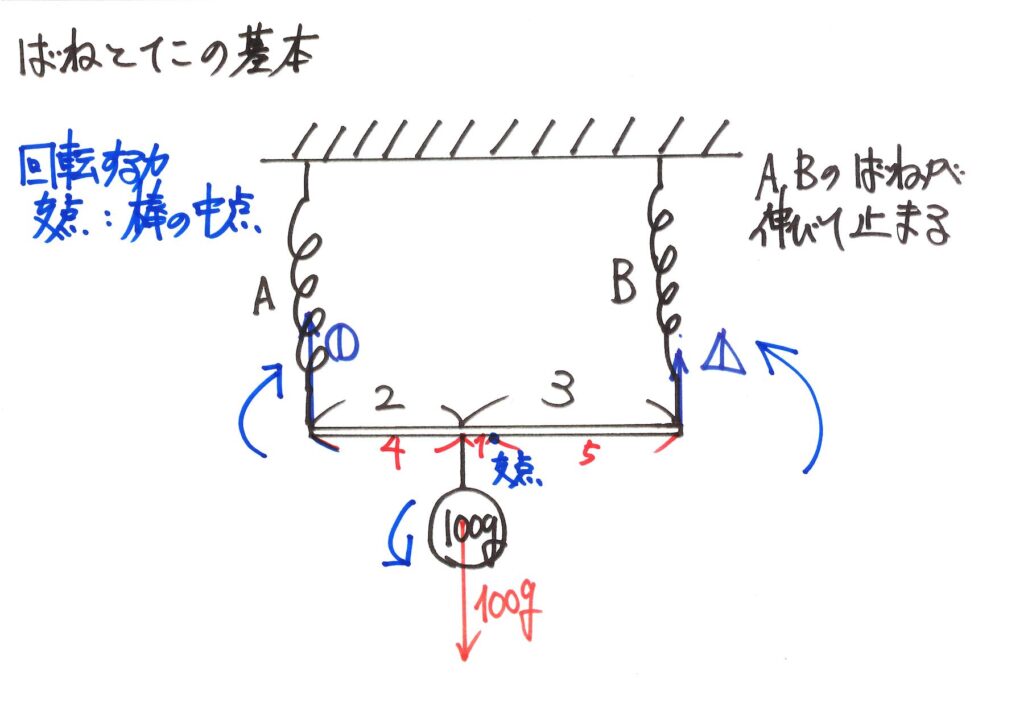
「難しい」と考えずに、時計回りと反時計回りの「回転する力」を考えましょう。
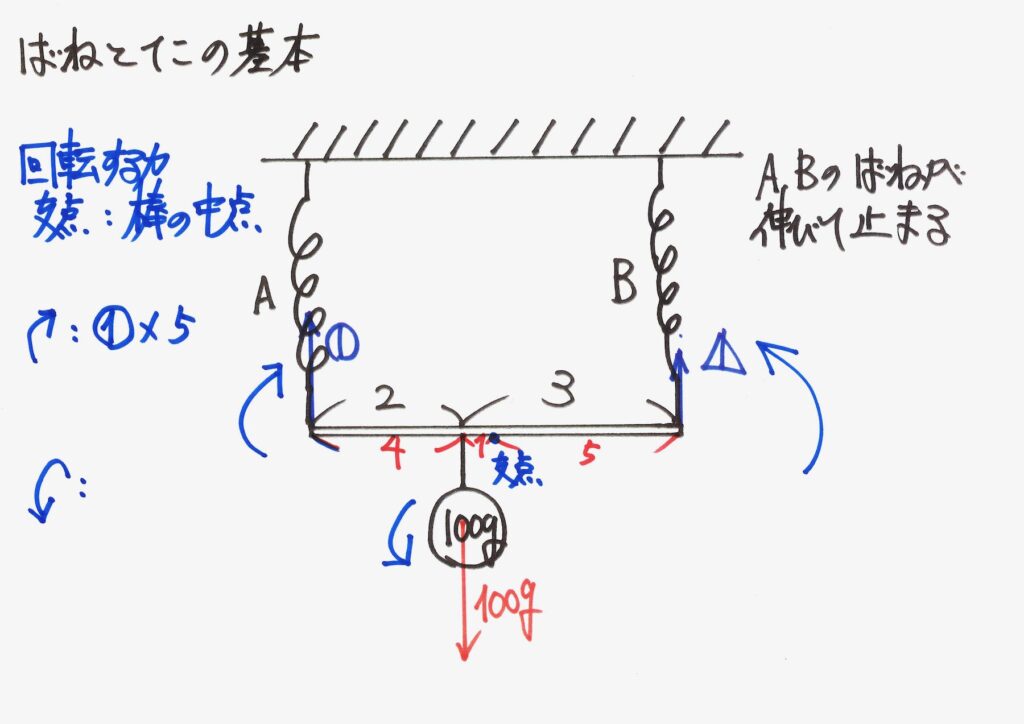
時計回りの「回転する力」は、バネAが引っ張る力だけです。
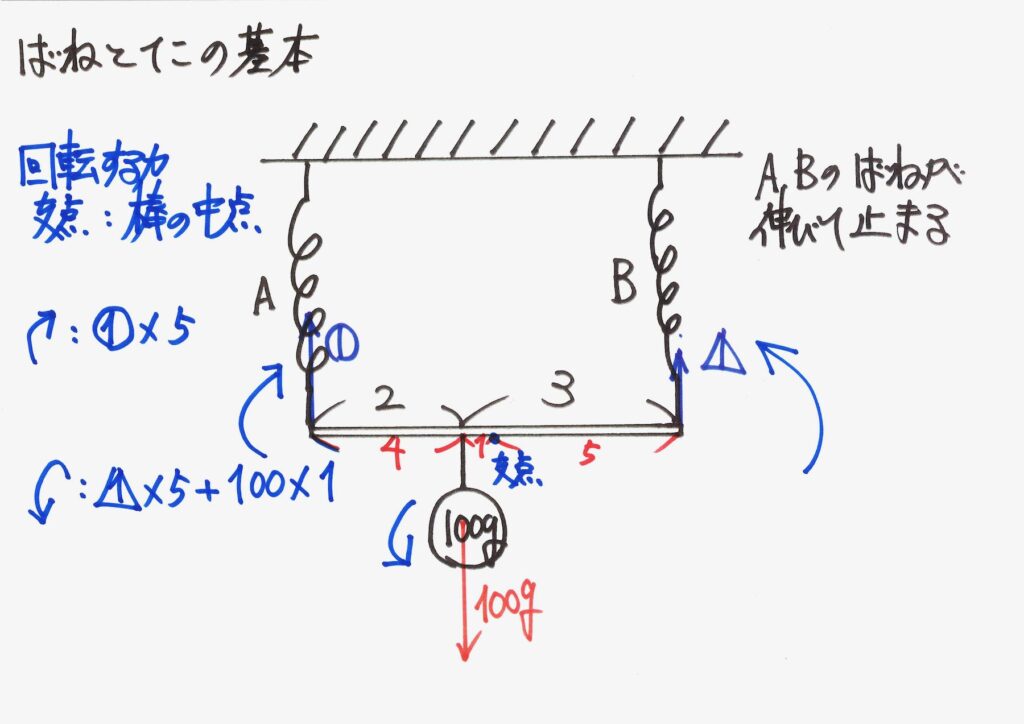
反時計回りの「回転する力」は、バネBが引っ張る力と、おもりの重さ（重力）がつくります。
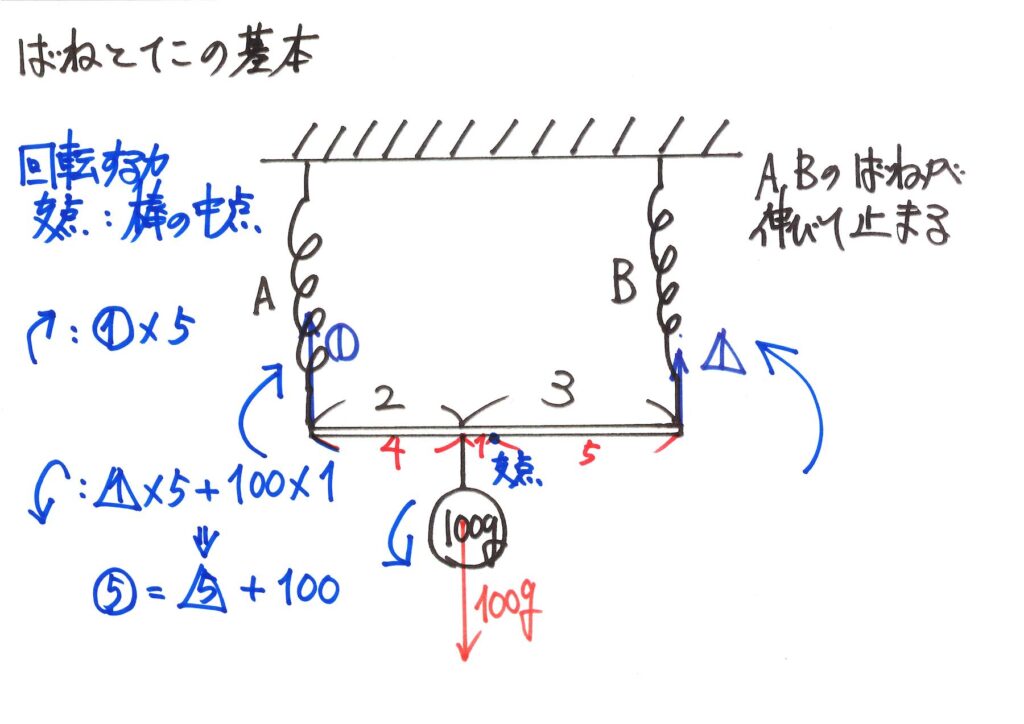
これらが等しいので、等式が出来ました。
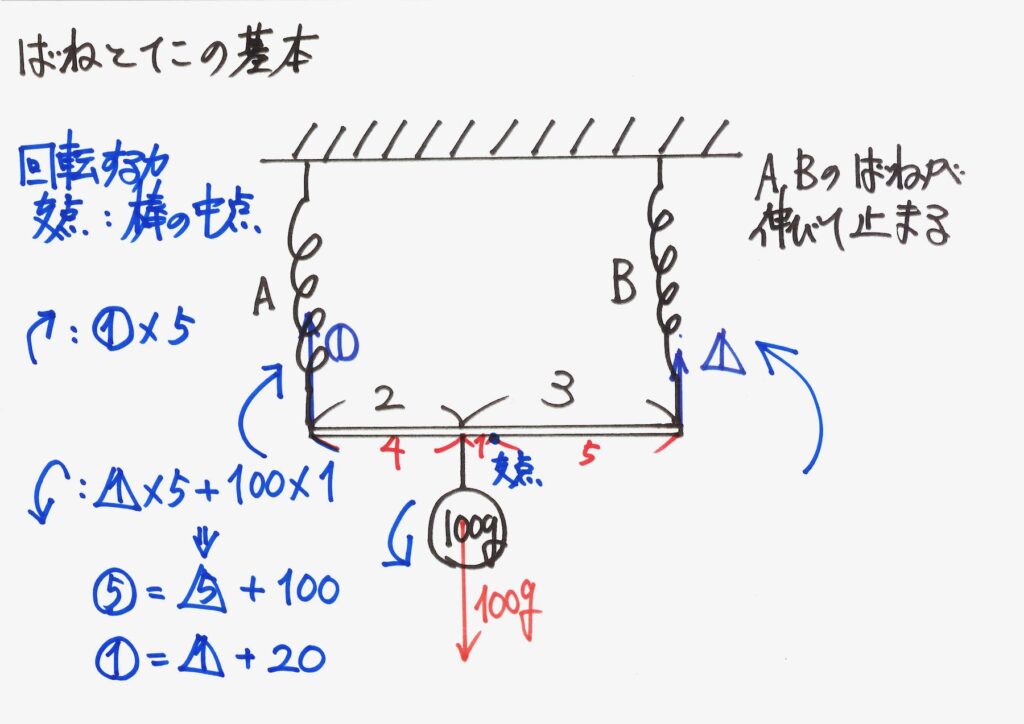
全部5の倍数なので、5で割って整理しておきましょう。
これで、「回転する力」を考えた結果の、条件式が求まりました。
女子小学生後は、
これまでと一緒だね。
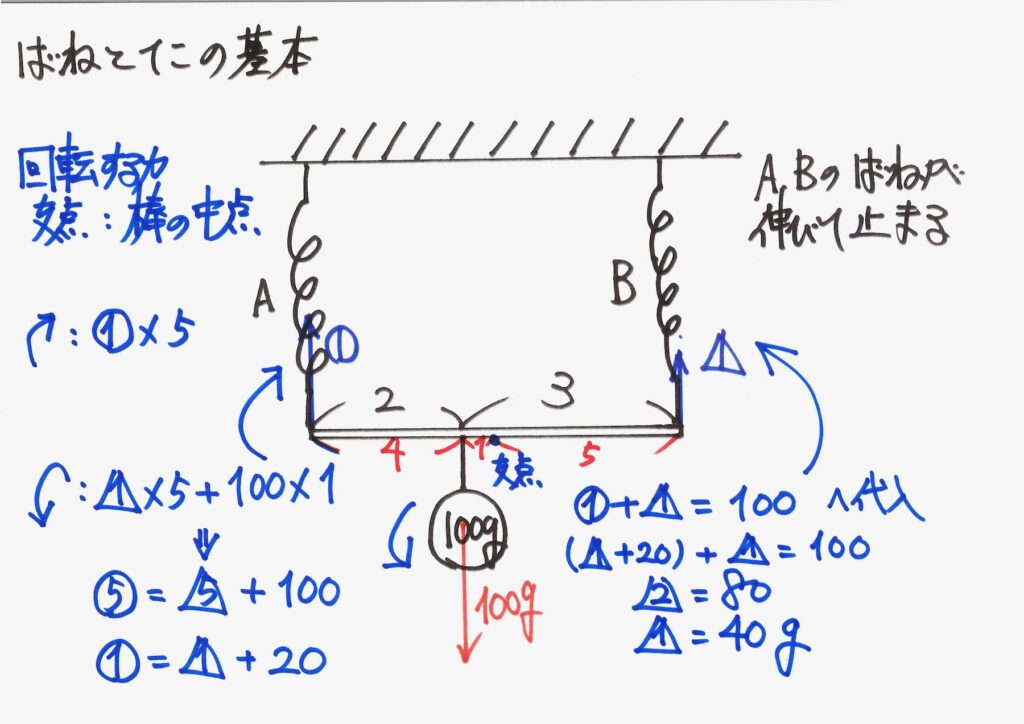
バネBの引っ張る力が求まり、同じ結果になりました。
女子小学生どこで考えても、
「つり合っている」から・・・
女子小学生同じ答え（結果）が
出るんだね！
女子小学生なんだか不思議で、
面白い・・・
考え方も計算もシンプルに
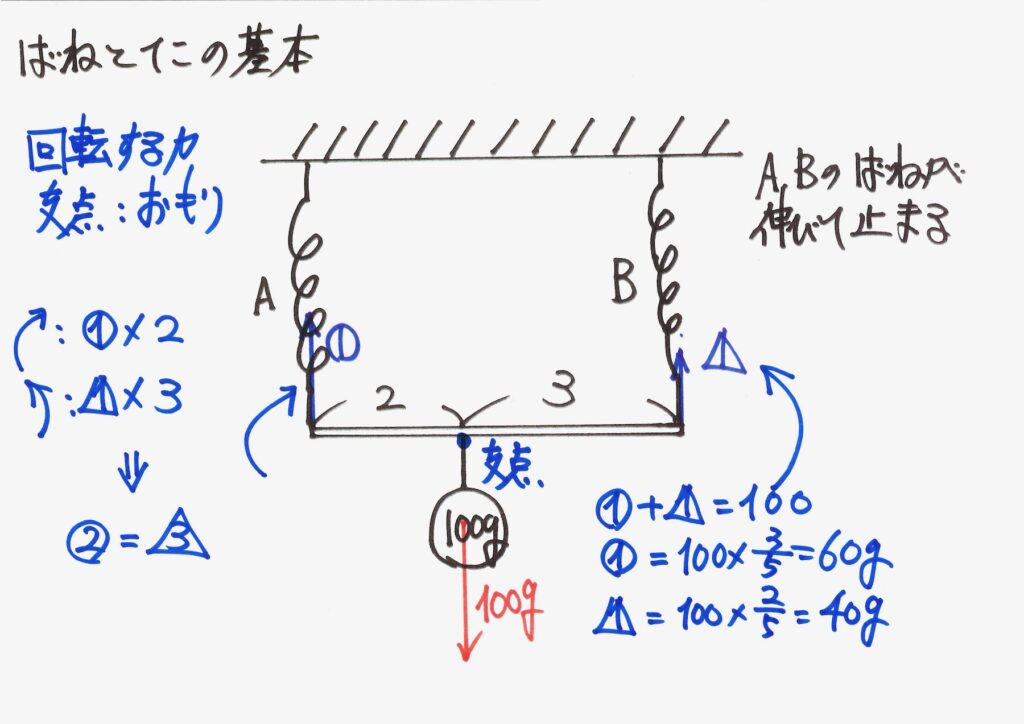
公式の「逆比」は、「おもりと棒のつながる点」を考えると求まります。
この考え方をしっかり理解していれば、「逆比」と暗記しなくても、分かります。
男子小学生うん。
よく分かった！
男子小学生よく分かったし、
公式の暗記も「間違えない」よ！
算数・理科の公式は「理解して習得する」と、「丸暗記」よりも学力がグンと上がります。
女子小学生「分かっている」から
間違えないのも良いね！
「ただ公式を丸暗記」していても、「使えなければ意味がない」のです。
こうして「公式を理解する」姿勢は、「公式の意味をしっかり理解する」ことにつながります。
今回、4つの点で考えてみました。
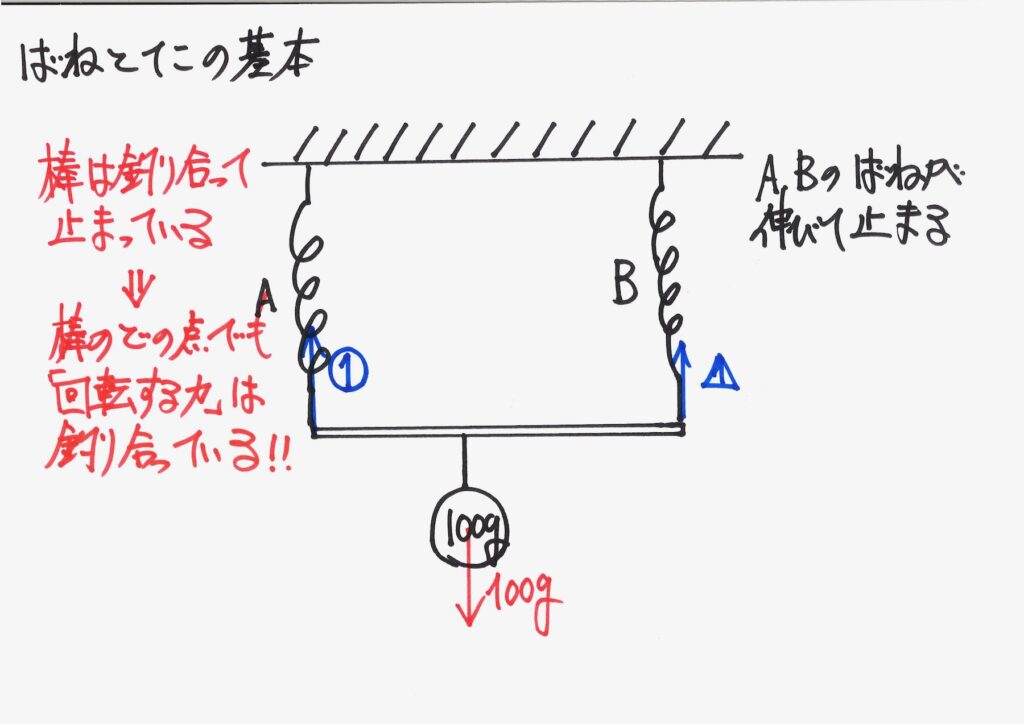
「棒が釣り合った状態」なので、他の点でも、考えてみましょう。
どの点で考えても同じ結果になりますが、計算過程が少し違いました。
女子小学生確かに
そうだね・・・
女子小学生最後の「棒の中点」が少し、
考えることが多かった・・・
どの点を考えても、「回転する力」は釣り合っているイメージを大事にしましょう。
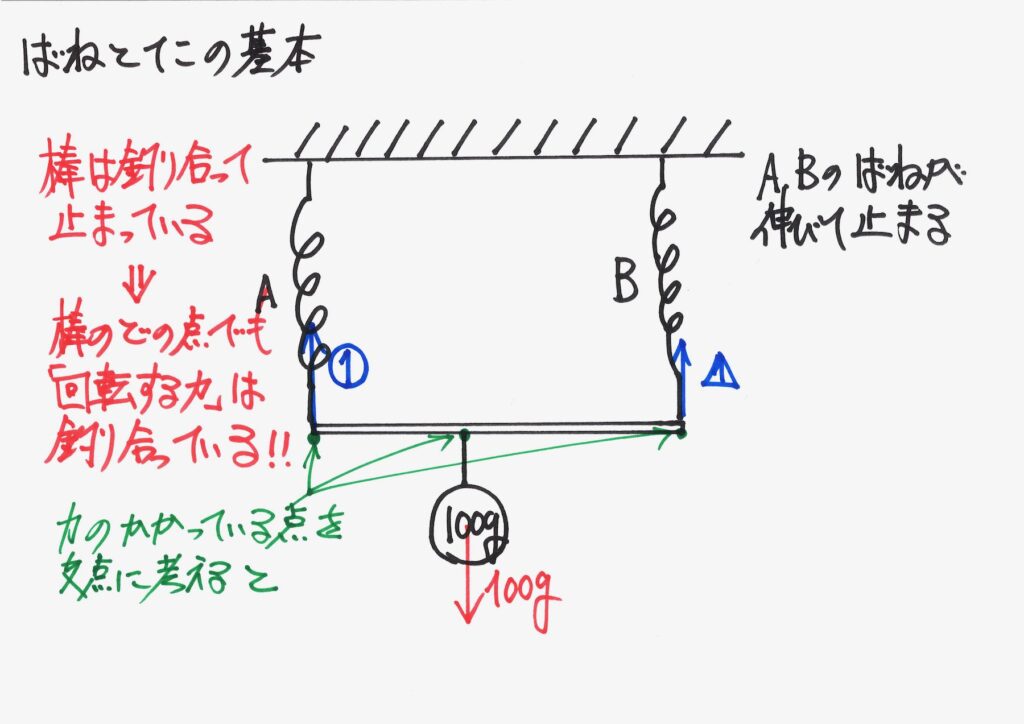
ここで、大事なことは、「力のかかっている点を中心（支点」に考える」と、どうなるか、です。
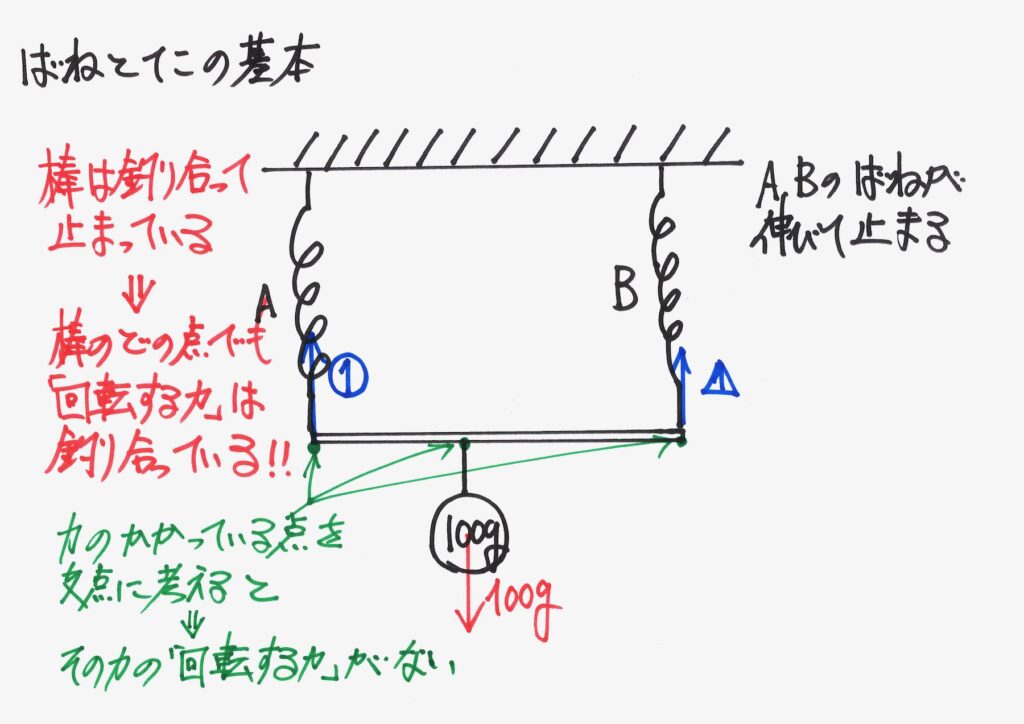
「その力と支点（中心）の長さ=0」なので、「回転する力」が出てこないです。
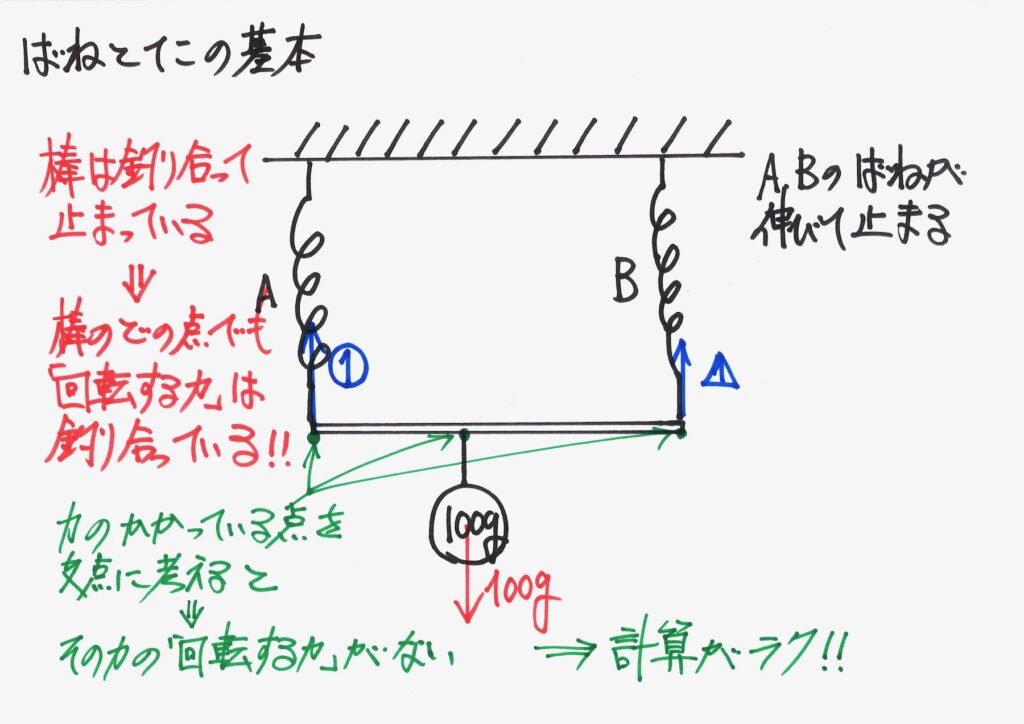
すると「考え方も計算も楽」なのです。
そして、考え方がシンプルになります。
なんでも「シンプルにする」ことは、非常に大事です。
本質的には、「どの点でも回転する力が釣り合っている」ことが大事です。
男子小学生楽な方が、
テストではいいね。
様々な考え方を身につけると、
女子小学生こう考えたら
良さそう！
「ここがポイントかな」という勘が磨かれます。
色々考えて、しっかり理解して学力を上げましょう。
次回は下記リンクです。
