前回は「ばね・てこのコツ・ポイント 1〜てことモーメント（回転する力）のイメージ・公式を理解する姿勢・「逆比」の説明・「つり合っている」=特殊な状況・支点を考える〜｜中学受験・理科」の話でした。
「棒の重さ」が「ある」と「ない」：「ない」に仮定して簡単に
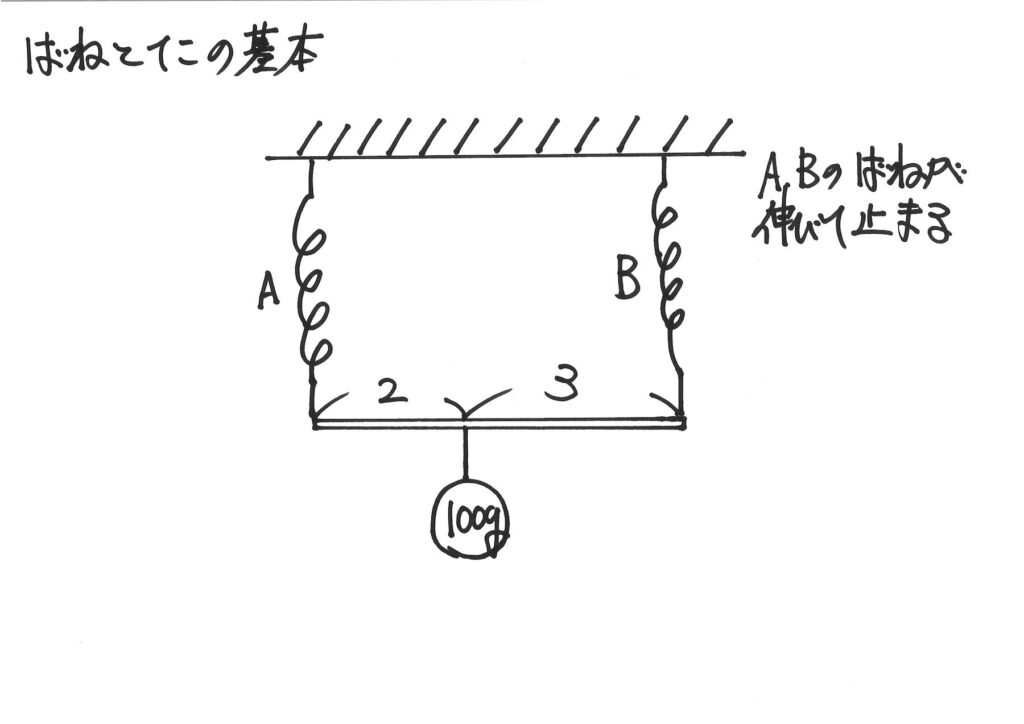
試験・テストでは、てこが登場すると基本的に「てこの棒」は水平です。
今回も「棒の重さは考えない」とします。
本来ならば、「棒の重さはある」のですが、簡単にするために「棒の重さはない」とします。
男子小学生確かに、「棒の重さ」は
あるはずだね・・・
男子小学生あるのに、勝手に
「ない」としてもいいの？
「現実の状況をしっかり考える」ならば、「ある」ものを「ない」とすることは✖️です。
上の状況を現実に考えると、「棒の重さはある」ので、「ない」として計算すると間違いになります。
女子小学生そうだよね・・・
じゃ、なぜ？
男子小学生間違っている
んでしょ・・・
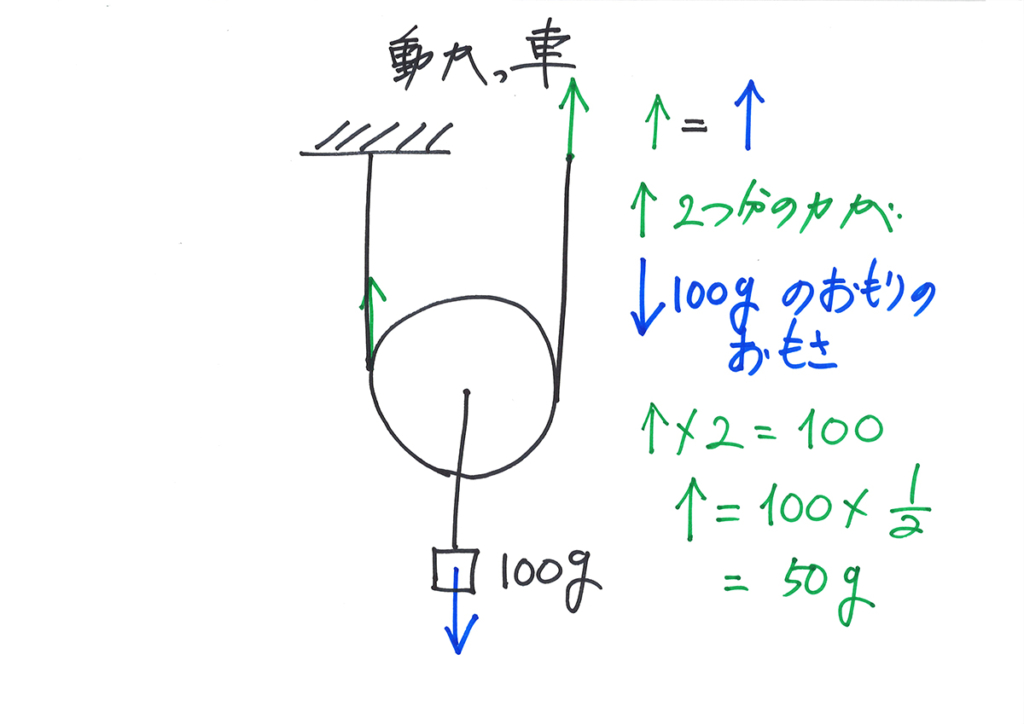
かっ車の時も、「当然のように」かっ車の重さを考えずに、おもりの重さだけ考えることが多いです。
男子小学生確かに
そうだね・・・
男子小学生定かっ車は
良さそうだけど・・・
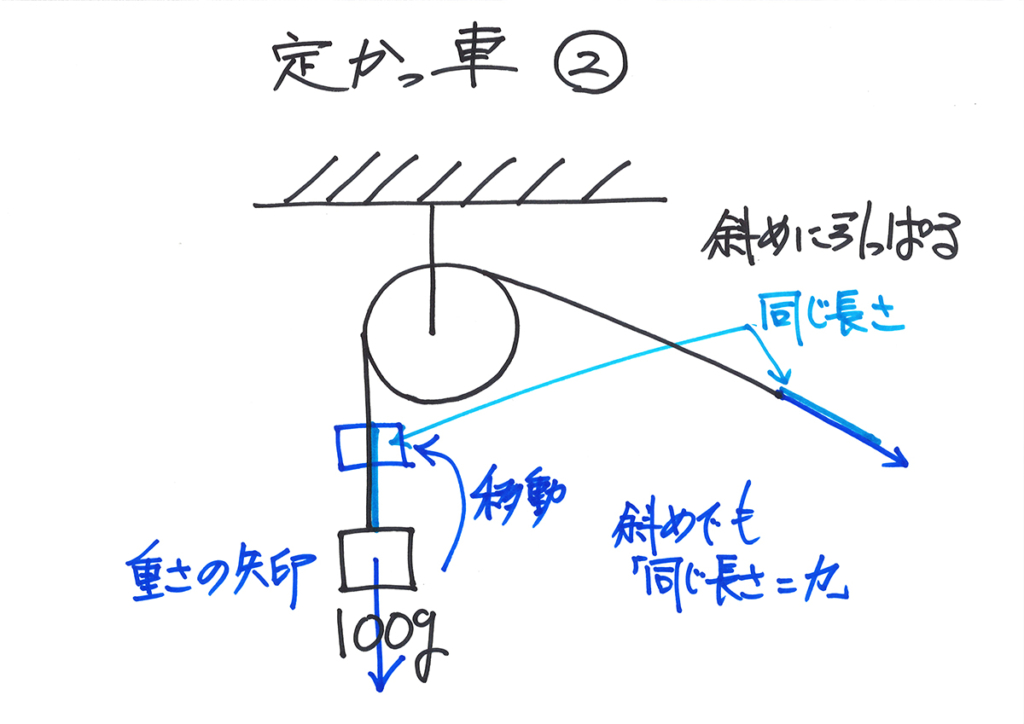
定かっ車の場合は、「かっ車の重さ」は天井が支えてくれます。
女子小学生じゃ、動かっ車の場合は、
かっ車の重さを考えないと、間違いでは？
現実世界に合わせると「ある」のに「ない」としているから、間違いになります。
男子小学生「間違い」で
いいの？
「間違うこと」は「点数が得られないこと」につながるので、受験生はどうしても気になります。
実は、このように「棒やかっ車の重さがないものとする」というのは仮定としては「正しい」です。
「正しいか間違っているか」と言うよりも、「そう仮定・決定した」上で考えています。
男子小学生じゃ、
いいんだ・・・
それは「状況を簡単にして、解けるようにする」ためです。
・「ある」ものを「ない」と仮定する、決定して考える
←「状況を簡単にして、解けるようにする」ため
上記のような棒とバネの問題で、「棒の重さを考慮する・考える」場合もあります。
その時は、「より現実に近い状況で考える」ことになります。
男子小学生じゃ、
そっち（棒の重さを考える）方が良いんだ・・・
これは「良い」とか「良くない」の問題ではなく、「どのように考えるか」の問題です。
そして、このような理科の現象は「少し簡単にして、大事なことを知る」ことも大事な姿勢です。
・状況を少し簡単にして、大事なことを知る
・複雑な状況に対して、簡単なモデルを想定して、本質的・大事なことを探す
「現実世界」は、かなり複雑です。
上のバネ・棒・おもりの問題で、「全ての状況を考慮」して「完璧を目指す」のは困難です。
「完璧」を目指す姿勢は大事ですが、「大体で良い」と言う姿勢も大事です。
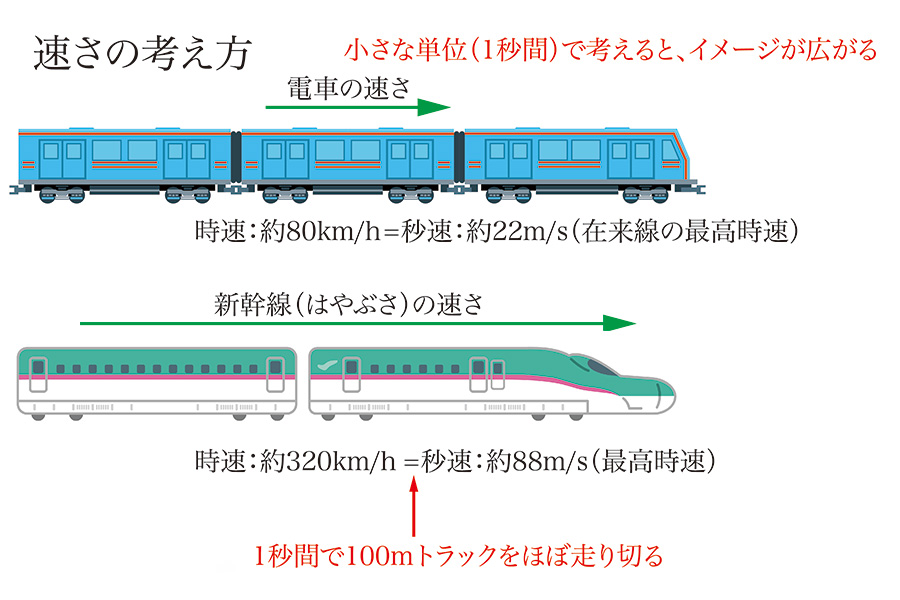
例えば、時速320kn/hの新幹線は、「秒速約88m/s」となります。
この「秒速約88m/s」に対しては、「速すぎてイメージが湧かない」です。
そこで、「たった1秒でシュッと、校庭の100mトラックを回る」イメージを持ちましょう。（上記リンク）
「88と100」では「全然違う」のですが、「秒速約88m/s」を実感するには「少しの違い」です。
理科の問題で「ある」ものを「ない」としているのか、していないのか。
そう言うことも、「少し気にする」と好奇心・興味が湧くでしょう。
例えば、「棒の重さを考えるのか、考えないのか」で答えも変わります。
男子小学生問題文を
気にするようにするね！
女子小学生てことかの問題では、図ばかり見て、
問題文はサラッと読んでいたけど・・・
女子小学生少し
注意して読むようにしよう！
「つり合っている」イメージ：異なる点でのつり合い
問題文では、「当然のように」つり合いがとれていて、真っ直ぐ水平な棒・てこ。
実際には、このような「つり合い」は不安定な場合が多くて、「つり合わない」こともあります。
「つり合わない」状況が登場する問題もありますが、大抵「つり合っている」です。
それもまた、「状況を限定して、簡単にしている」とも言えます。
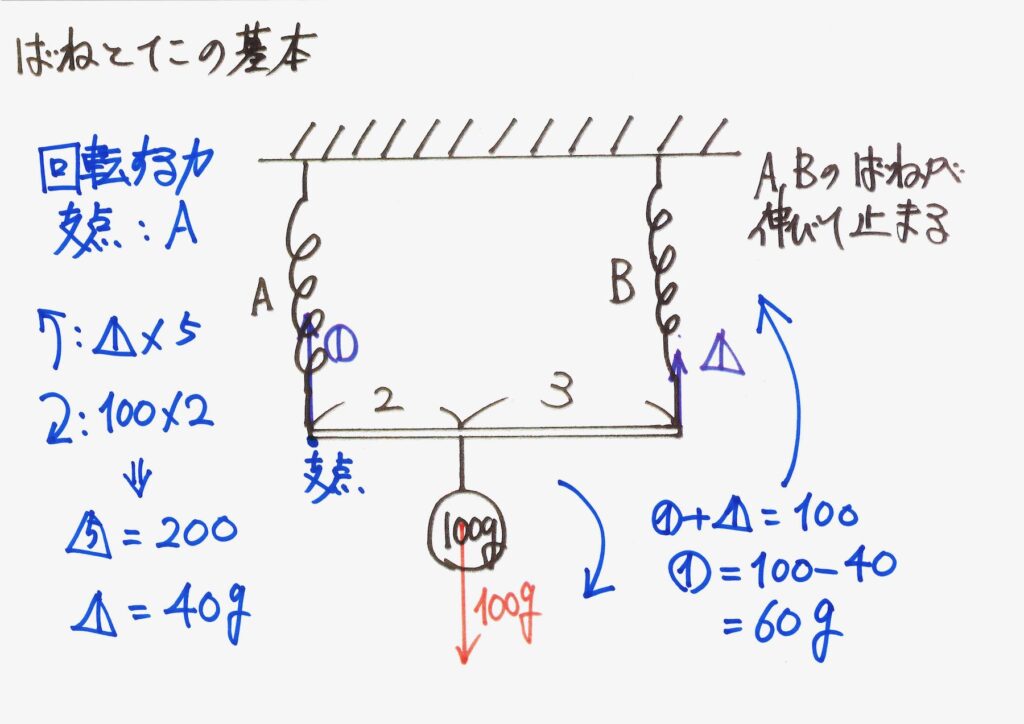
今回は、バネBと棒の繋がっている点を中心に、「回転する力」を考えてみましょう。
前回は、バネAと棒の繋がっている点が「つり合っている」ことを考えました。
そして、この点を中心とする「モーメント・回転する力」を考えました。
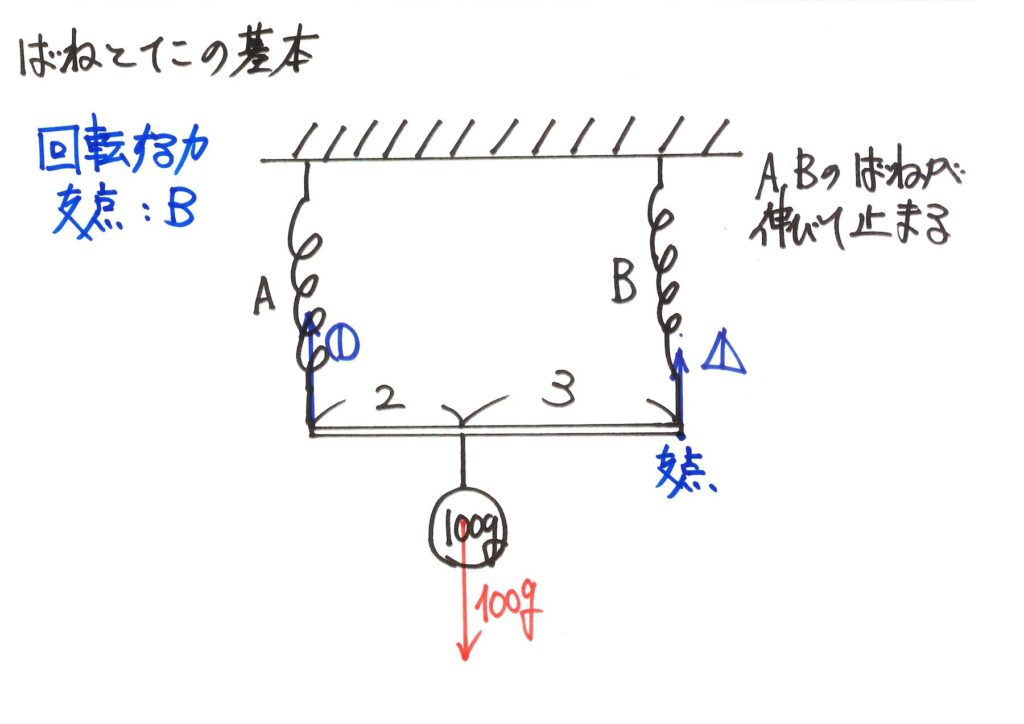
今回はバネBと棒の繋がっている点が「つり合っている」ことを考えましょう。
上の図でその点を明確にするために「支点」と描いていますが、「仮想的支点」です。
「本当はない支点」ですが、「ここを中心とするモーメント・回転する力」を考えるイメージです。
この点はつり合っていて、止まって（静止して）いるので、モーメント・回転する力はないはずです。
バネAが引っ張る力が時計回りの「モーメント・回転する力」を生み出します。
そして、おもりの重さが反時計回りの「モーメント・回転する力」を生み出します。
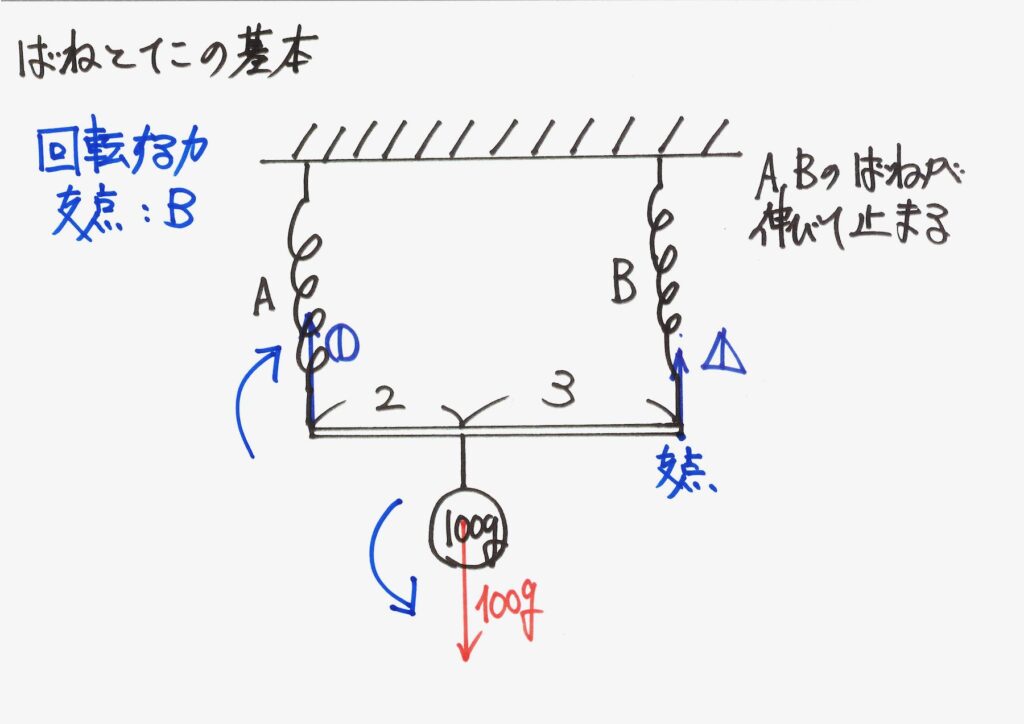
「回転する力」を「回転する矢印」で表現しましょう。
重さ・力とモーメント・回転する力は、性質が異なります。
そこで、慣れるまでは、色鉛筆・マーカーなどで色を変えると良いでしょう。
このように「色で分ける」と言うのは、学ぶ過程では大事なことです。
「仲間・似たようなもの」に対しては、「同じ色」で表現します。
・「仲間・似たようなもの」に対しては、「同じ色」
・「仲間ではない・似ていないもの」に対しては、「違う色」
水溶液などの性質を覚える際にも、「色分け」は良いでしょう。
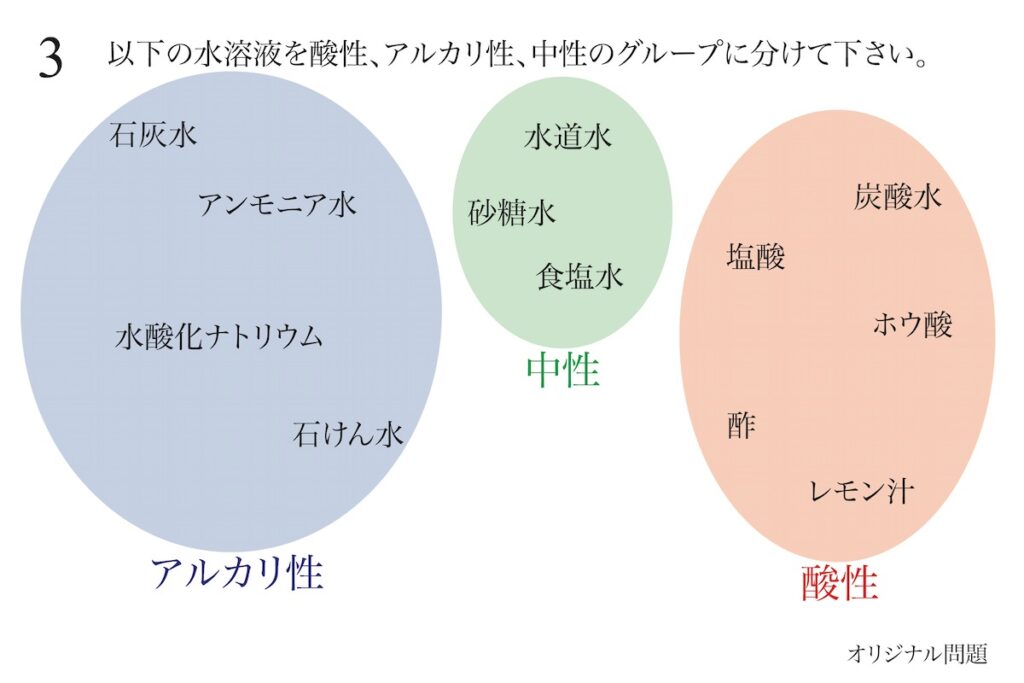
「語呂合わせ」などで覚えても良いですが、「色で覚える」のも良いでしょう。（上記リンク）
「同じ性質」と「違う性質」は色でイメージすると良いでしょう。
上のような絵がテキスト・参考書などにあれば、それでも良いですが、「自分で描く」のが大事です。
少し時間がかかりますが、自分で描くと「不思議と頭に入りやすい」のです。
そして、
男子小学生水酸化ナトリウムは、
青グループだったから・・・
男子小学生水酸化ナトリウムは、
アルカリ性だ！
語呂合わせではなく、自分で作った絵・図が頭にあると強いでしょう。
回転する力（モーメント）をイメージして、それぞれ計算します。
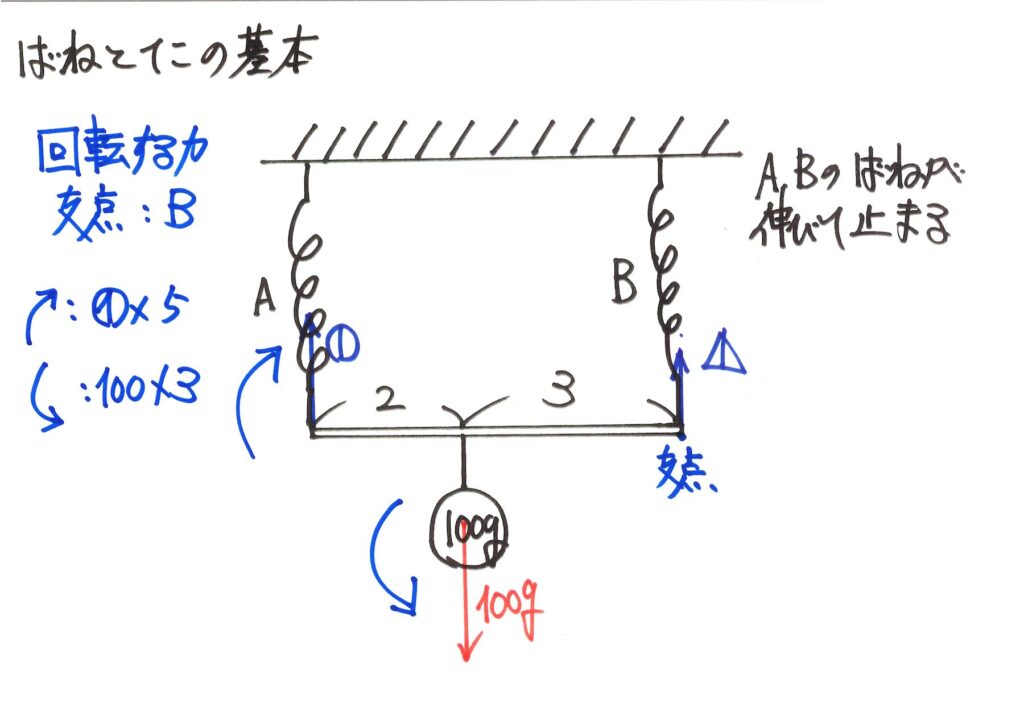
そして、時計回りの「回転する力」と反時計回りの「回転する力」が等しいので、計算できます。
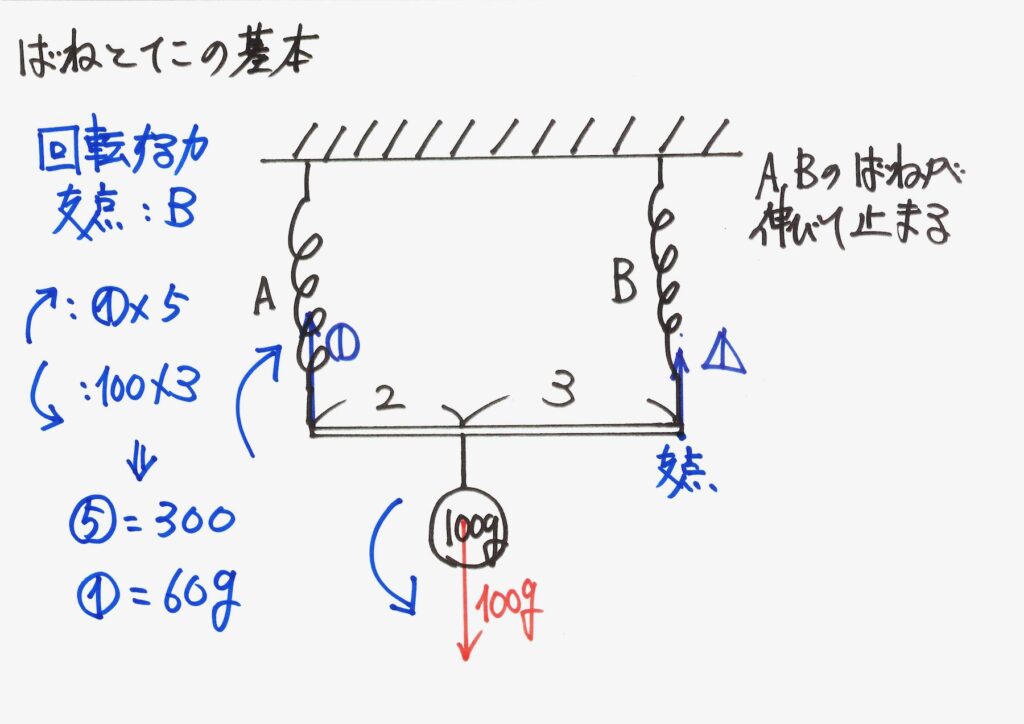
これで、バネAが引っ張る力が分かります。
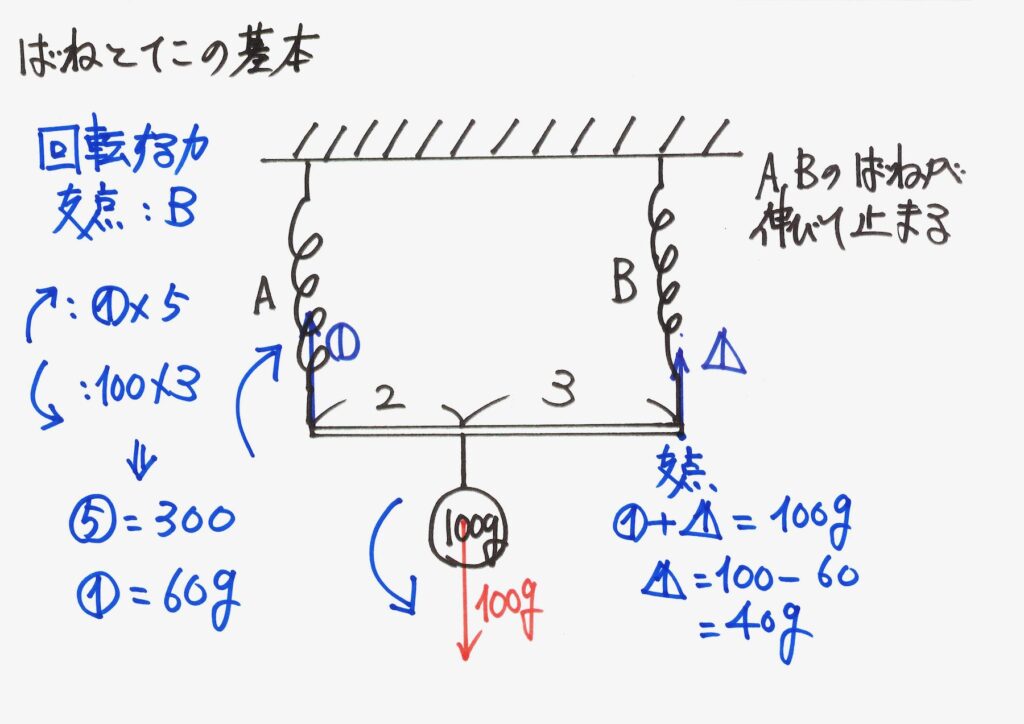
「バネA,Bの引っ張る力の和＝おもりの重さ」なので、バネBの引っ張る力も分かります。
他の点でのつり合いを考える
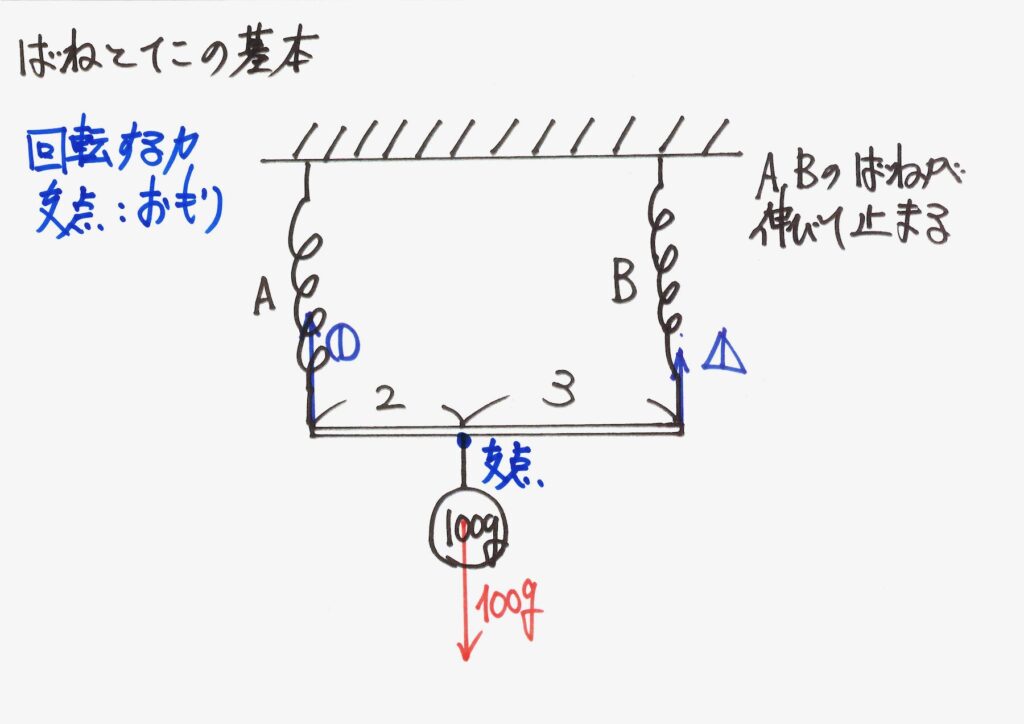
今度は、「おもりの下がっている点」を中心に考えてみましょう。
この点も「つり合っていて、止まっている（静止している）」状態です。
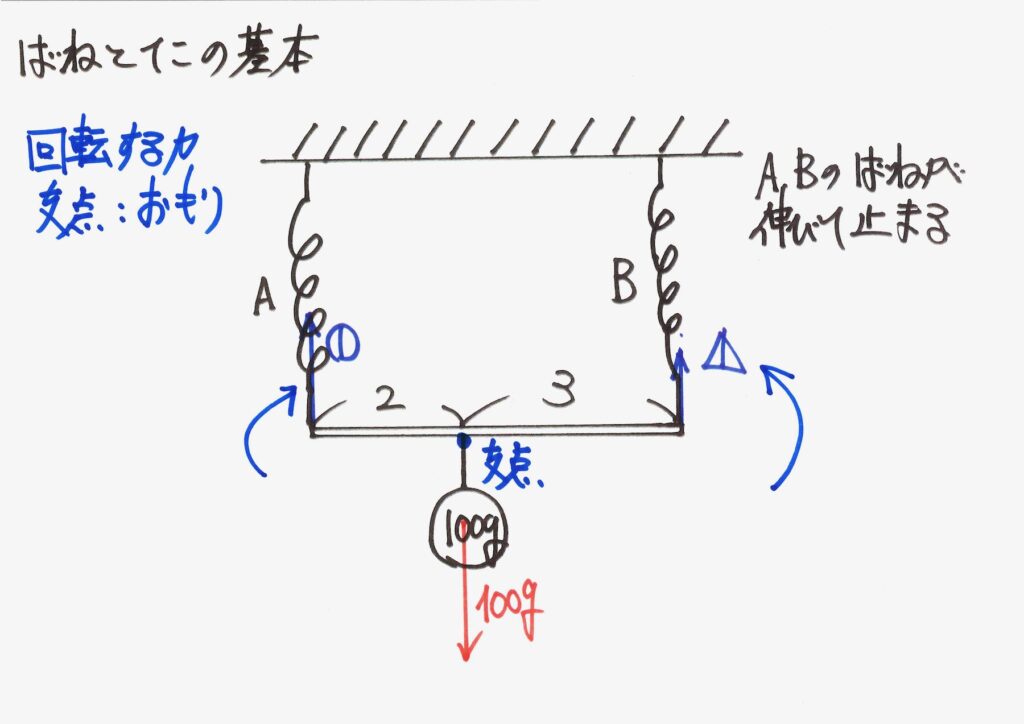
バネAが引っ張る力が反時計回りの、バネBが引っ張る力が時計回りの「回転する力」をつくります。
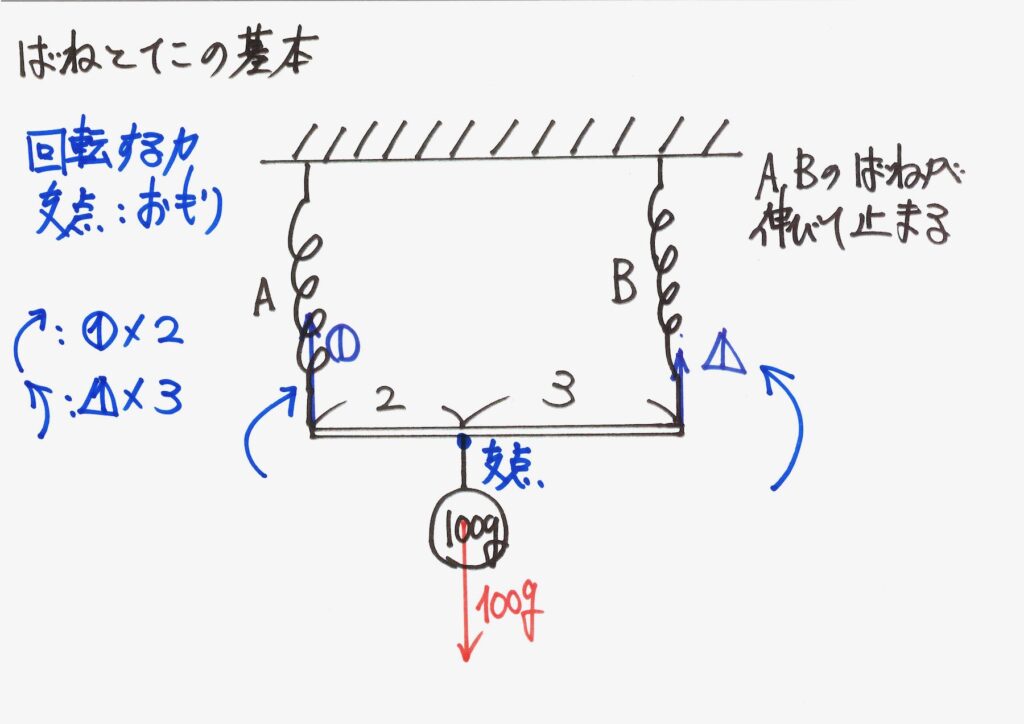
それぞれの「回転する力」を計算しましょう。
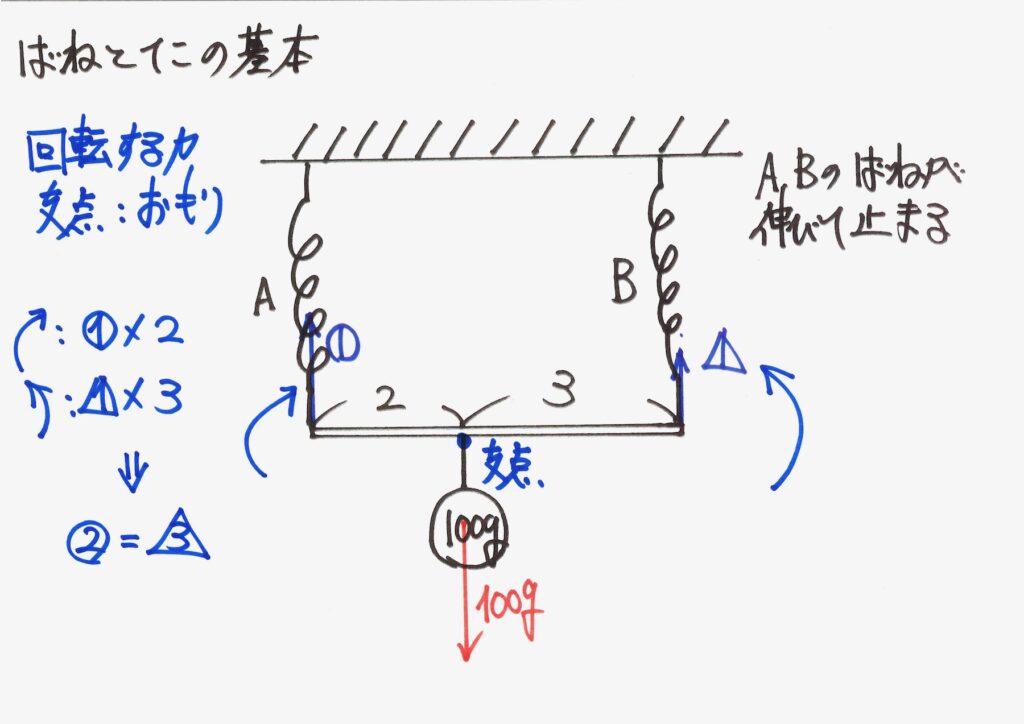
これらが等しいので、バネA、Bの引っ張る力の関係式が分かりました。
男子小学生あれ？
さっきまでと違って、求まらないよ。
女子小学生和が分かっているから、
計算できる！
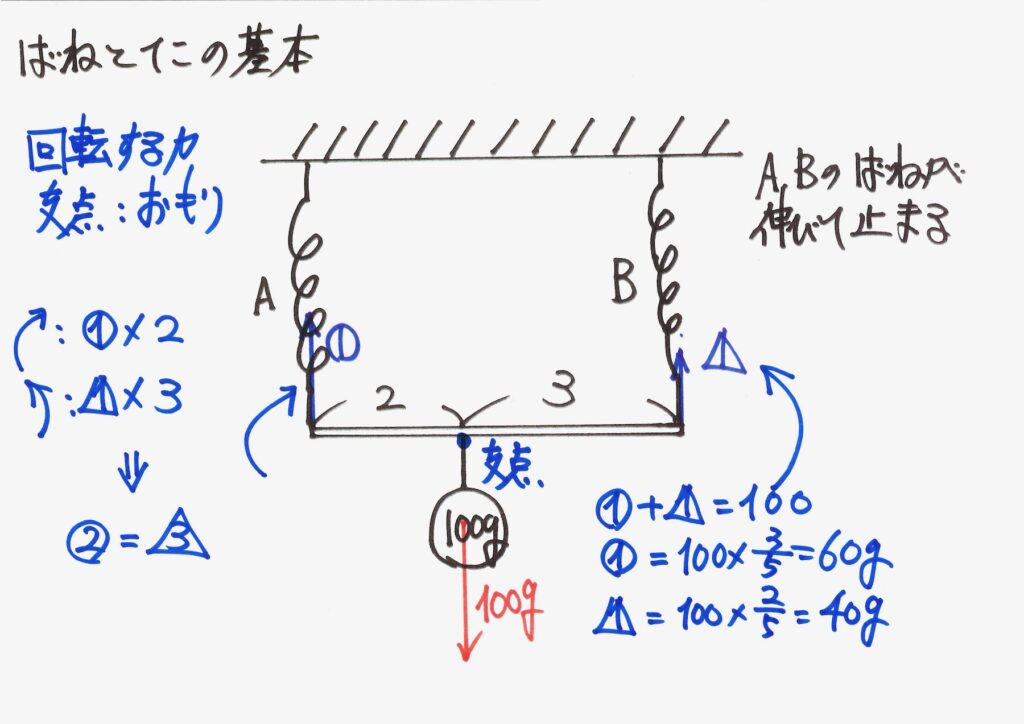
バネA,Bの引っ張る力が、求まりました。
男子小学生ひょっと
して・・・
男子小学生ここで考えたことは、
公式と一緒だ！
女子小学生「逆比」って、
こういうことだったのね。
このように、「おもりの点でのつり合い」を考えると、「力は長さの逆比」の公式がわかりました。
それでは、次回は棒の中点で「回転する力」を考えてみましょう。
次回は下記リンクです。
