前回は「ばね・てこのコツ・ポイント 3〜モーメント・「複雑」を「簡単」に・重心・中心・考え方も計算もシンプルに・公式の理解・逆比〜」の話でした。
てこ・バネのつり合い：全ての棒の点でのつり合い
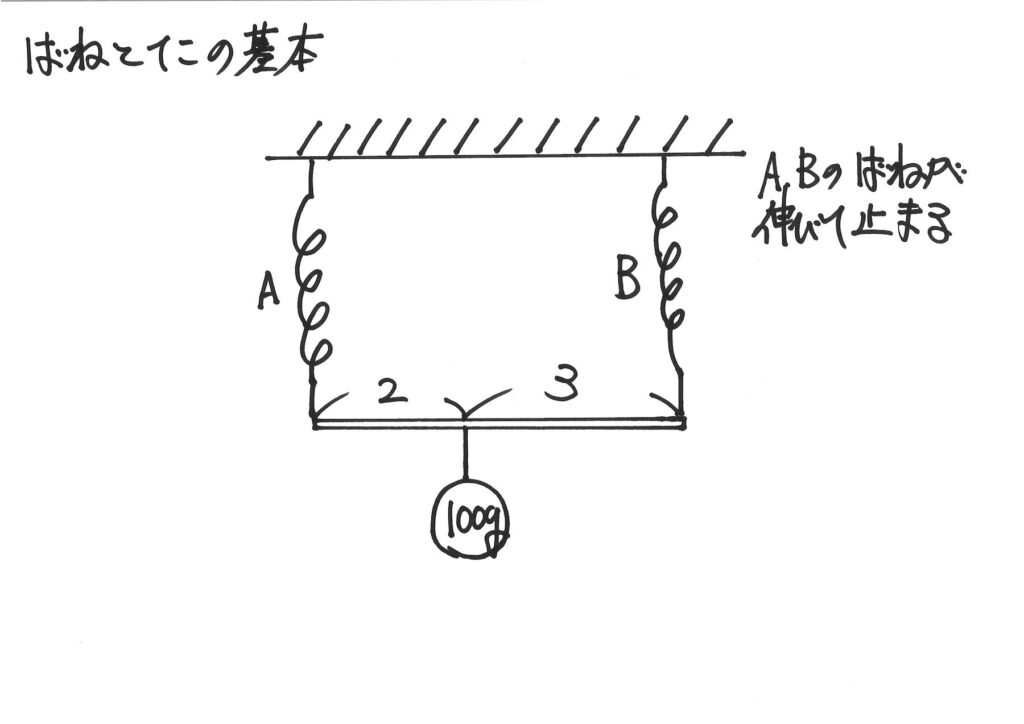
上のような「バネとてこの基本」の問題を考えましょう。
この問題に対しては「長さの逆比」を考えて、「それぞれのバネにかかる力」が計算できます。
公式である「逆比」は、ただ「丸暗記するのではなく、意味を理解する」のが大事です。
上のようなバネとてこは、「バネが伸びて、てこの棒とおもりを支えてつり合う」です。
今回は、棒の重さを考えませんでした。
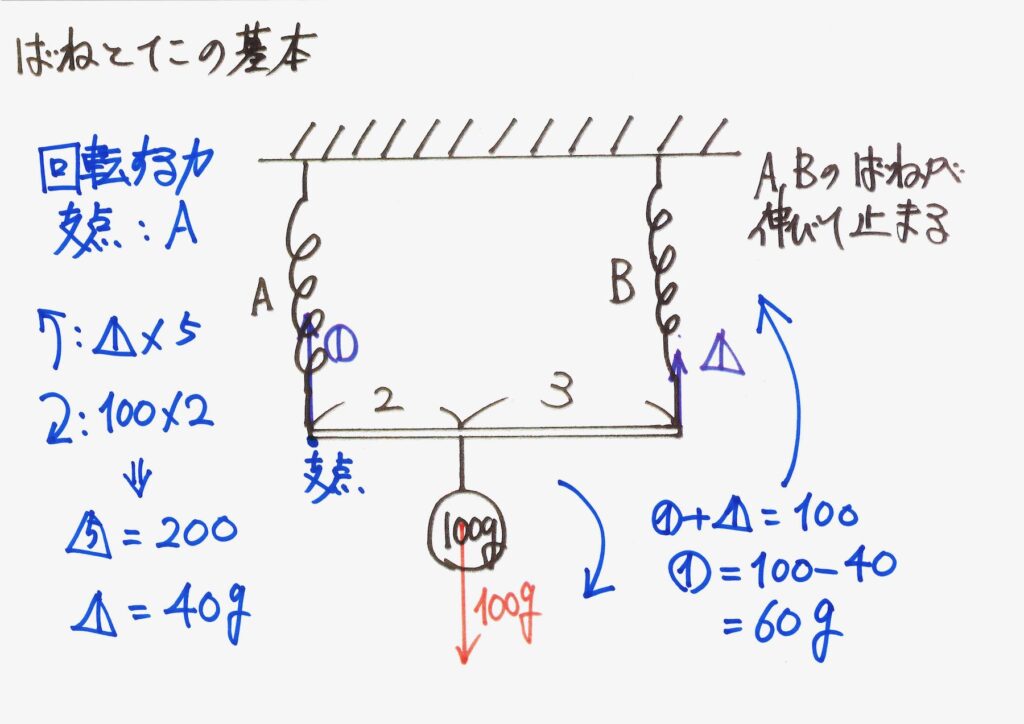
バネAと棒の接点を中心に「モーメント（回転する力）のつり合い」を考えても、
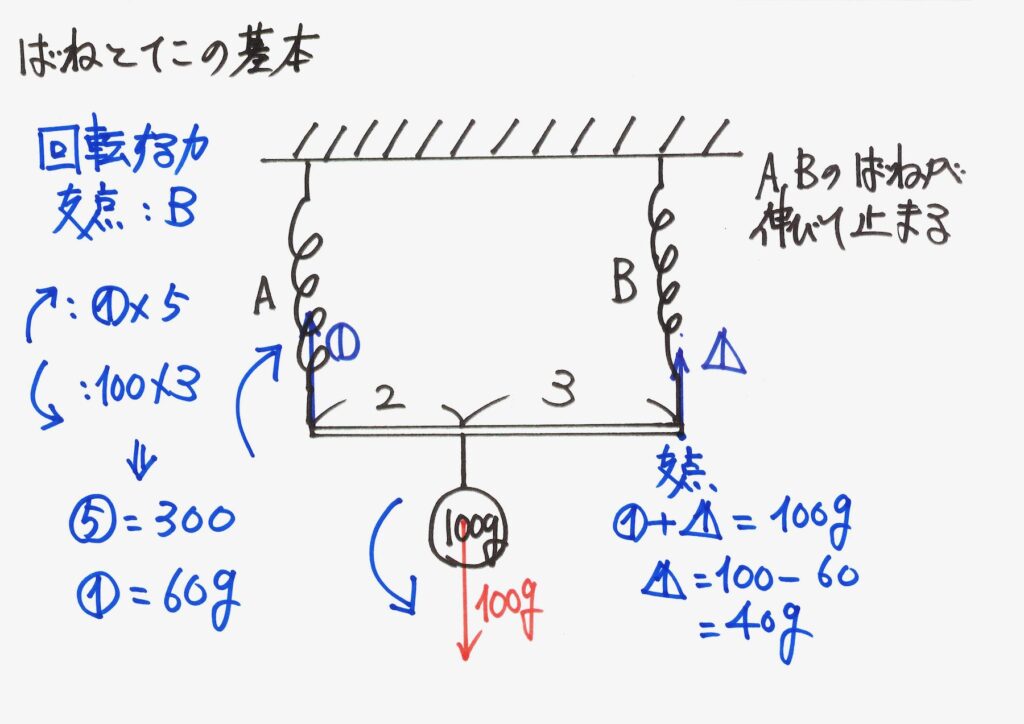
バネBと棒の接点を中心に「モーメント（回転する力）のつり合い」を考えても、
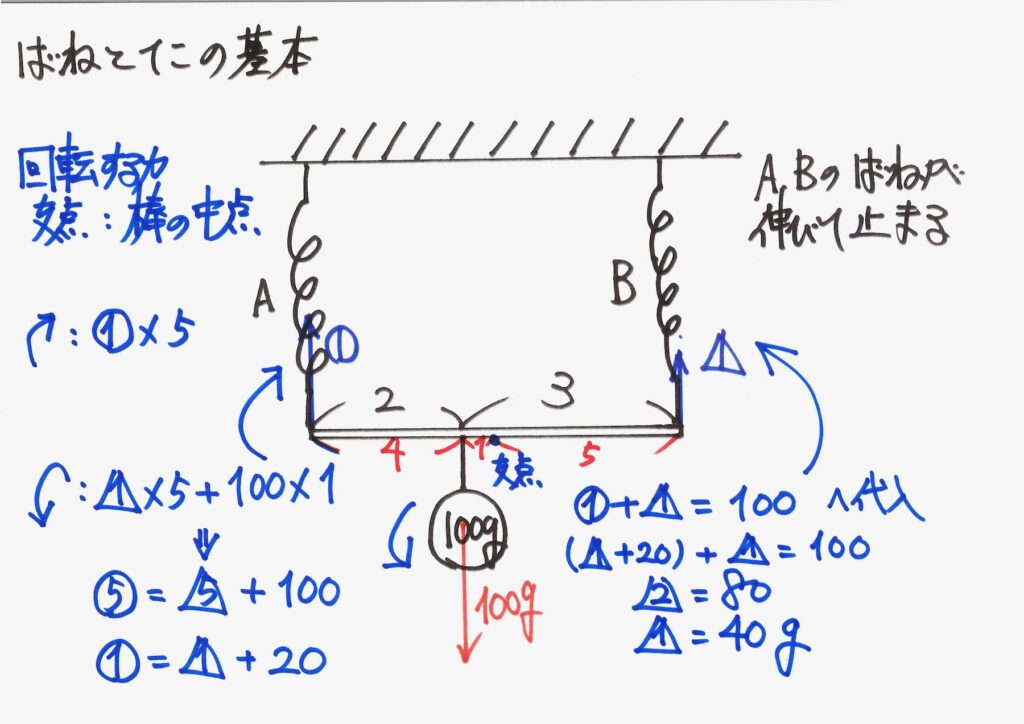
棒の中央を中心に「モーメント（回転する力）のつり合い」を考えても、
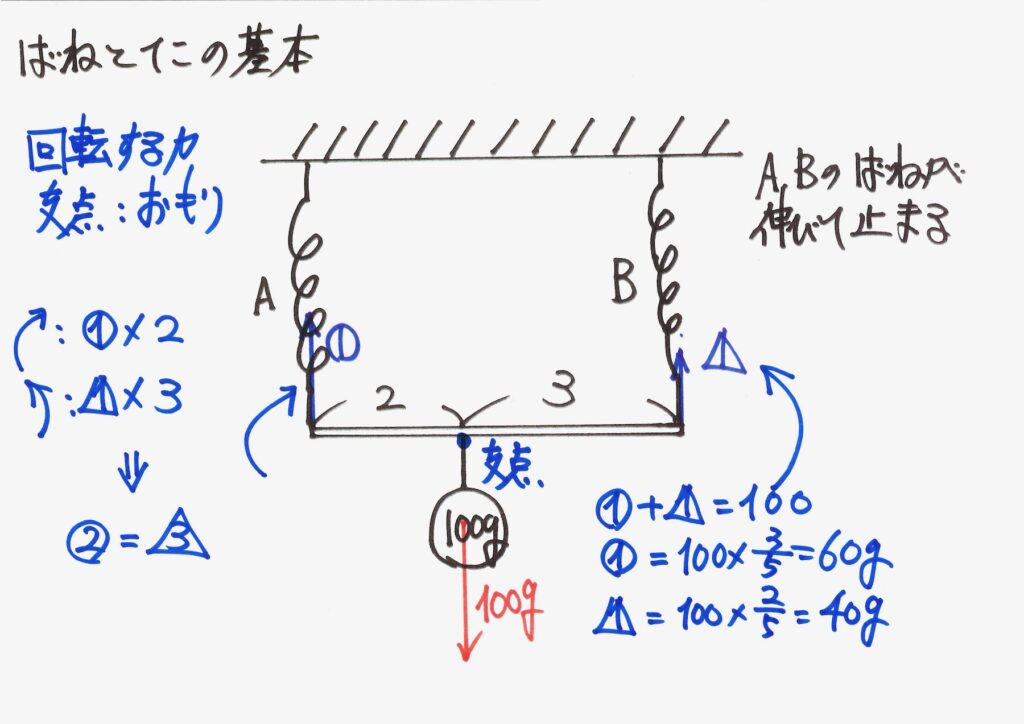
おもりがつり下がる点を中心に「モーメント（回転する力）のつり合い」を考えても、同様です。
どこの点を中心に、「モーメント（回転する力）のつり合い」を考え、計算しても解けます。
「解けた」のは計算の結果に過ぎず、そもそも「棒のどの点でもつり合っている」ことが大事です。
上記の四つの場合において、「どの場合で考えても良い」です。
「良い」というよりも、「バネとてこ（棒）の状況を把握する」には、「どの点で考えても同じ」です。
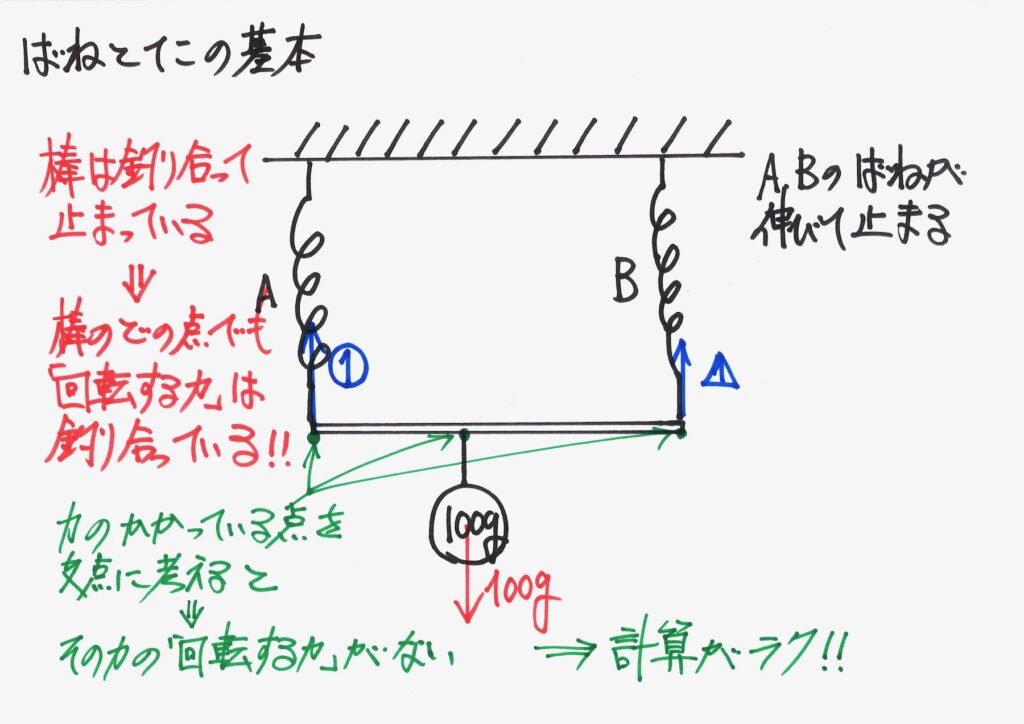
「どの点でも同じ」ですが、最後の「おもりがつり下がる点」で考えると、最も簡単でした。
「棒にかかるおもりの重さ」があるから、バネが伸びてつり合う状況になります。
そこで、「おもりの重さ（重力）を発生させる点」に注目すると「逆比」が分かります。
2本のバネが支える「おもりの重さ100g」（棒の重さは0）よりも、「支える重さの比」が大事です。
・重さ（重力）を発生させる点（おもりと棒の接点）に注目
・回転する力（モーメント）を考えて、「長さの逆比」に「かかる力」を分配
このように考えると、問題が複雑になって、バネ・てこが沢山あっても「同じように解ける」はずです。
バネ・てこが沢山ある時も、「重さ（重力）を発生させる点（おもりと棒の接点）」に注目しましょう。
上記の四つの場合で、「全てのつり合いを考える」のは遠回りであったかも知れません。
「一つを考えれば出来る」のに、わざわざ「四つの場合のつり合い」を考えた理由がここにあります。
「どのように考えても、本来解けるはず」の理科・物理の問題です。
一方で「解きやすい考え方・ポイント」は、どの分野にもあります。
・重さ（重力）を発生させる点（おもりと棒の接点）の回転する力（モーメント）
・「かかる力」=「長さの逆比」、または「長さ」=「かかる力の逆比」
この「逆比」をしっかり理解しましょう。
これまでの「棒のどこの点でもつり合う」ことをしっかり理解しましょう。
「つり合う」ことは「普通ではないこと」であり、非常に安定して静止しているイメージです。
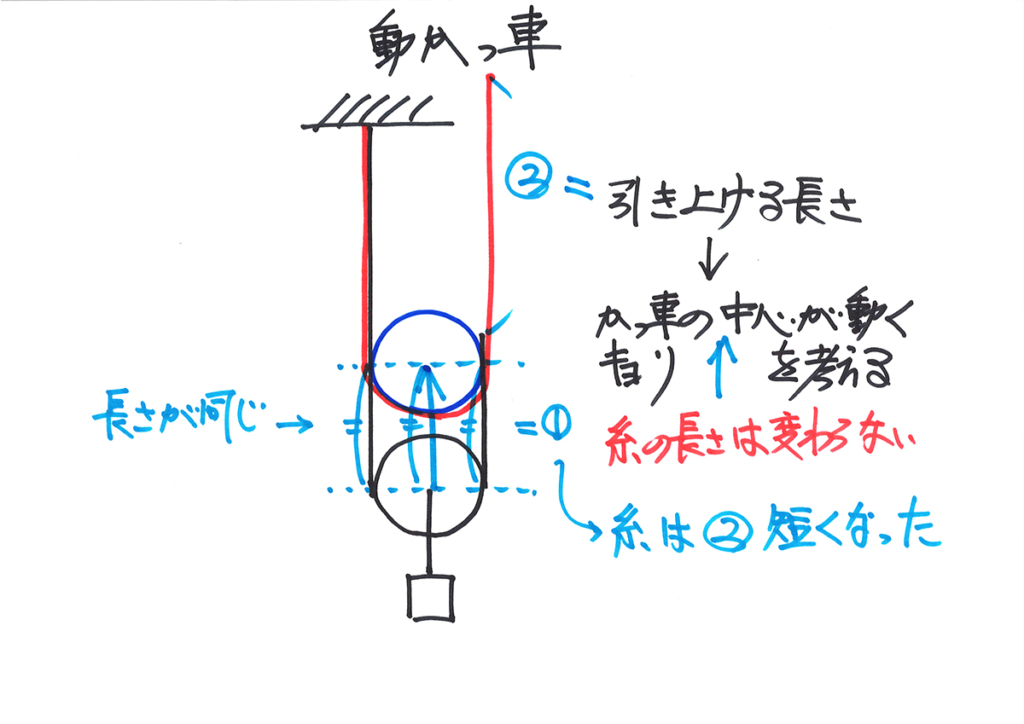
この意味では、かっ車も似ている面があり、「つり合っている」のです。
・「つり合う」ことは、その関係する部分（棒など）の沢山の場所で「つり合っている」
・「つり合っている」のは、非常に安定して静止（止まっている）しているイメージ
太さが一様ではない棒：類似点と理科への探究心
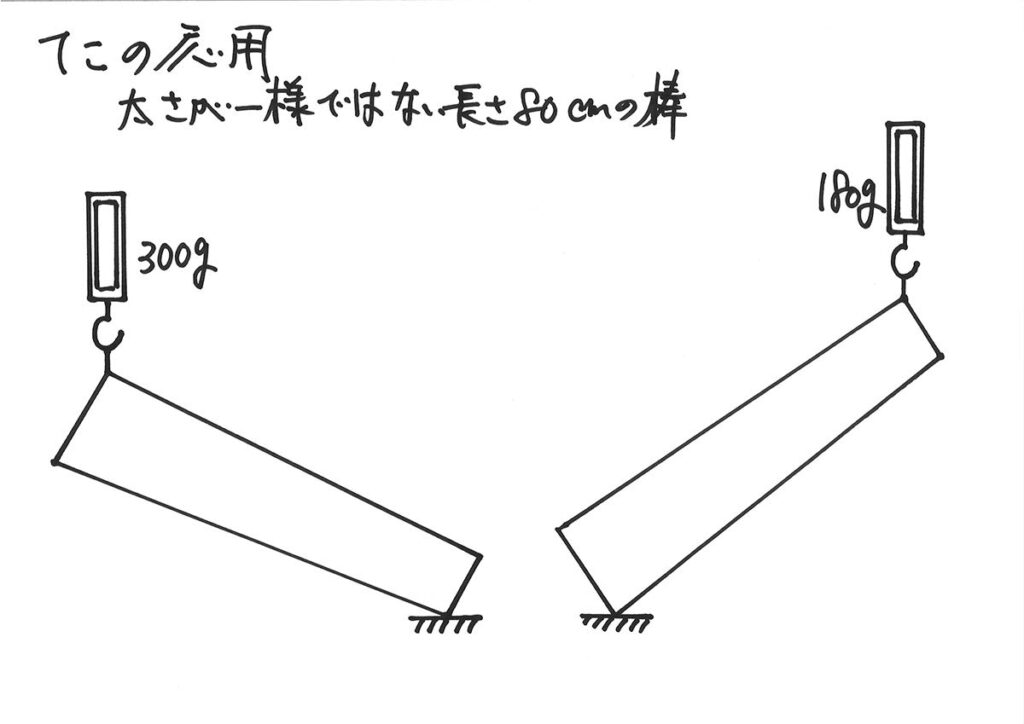
これまでは、「一様で、重さのない棒」を考えました。
今回は、上記のような「一様でなく、重さのある棒」を考えます。
この棒の重さと、重心の位置を考えましょう。
男子小学生これは、
知ってるよ。
男子小学生「両方の重さの和」
だよね。
ここで、「暗記」ではなく「理由を説明」することを考えましょう。
女子小学生これは、
「そういうものだ」と習ったわ。
女子小学生釣り合う場所も
「逆比」と習ったのと同じ感じ・・・
男子小学生そういえば、前に「逆比」の理由を
考えたけど・・・
女子小学生そうね。
同じように考えられないかな？
「同じように考える」という視点は、理科では非常に大事です。
「理科への探究心」は、中学生以上の勉強において、とても大事になってきます。
小学生の間に「理科への探究心」の基本を育てることができると、とても良いです。
全く異なる現象は別として、「似ている現象の類似点を考える」ようにしましょう。
電気は「電圧を考えてから電流」という話をしました。（上記リンク）
電気・電流は複雑な問題が沢山ありますが、「似たように考えてみる」と分かる問題も多いはずです。
男子小学生うん。
そうしてみるね。
算数・理科の基本問題は、「それぞれの分野の考え方に応じて、学ぶ」必要があることが多いです。
そして、算数・理科の応用問題は「基本問題の発展形」であり「類似性がある」のです。
・応用問題には類似性がある
・応用問題は基本問題の発展形・変化球、あるいは複数分野の複合形
・応用問題に対しては、「基本に振り返る」姿勢で考えると、ほぼ全て「同じ」か「似ている」
この問題の「棒の重さ」を考えてみましょう。
男子小学生まず、「重さが和」というのが、
なんとなく、そうかな？と思うよ。
女子小学生そうね。
「本当かな？」と思うけど・・・
重ね合わせる=二つの状況を足す：矢印で重さを表現
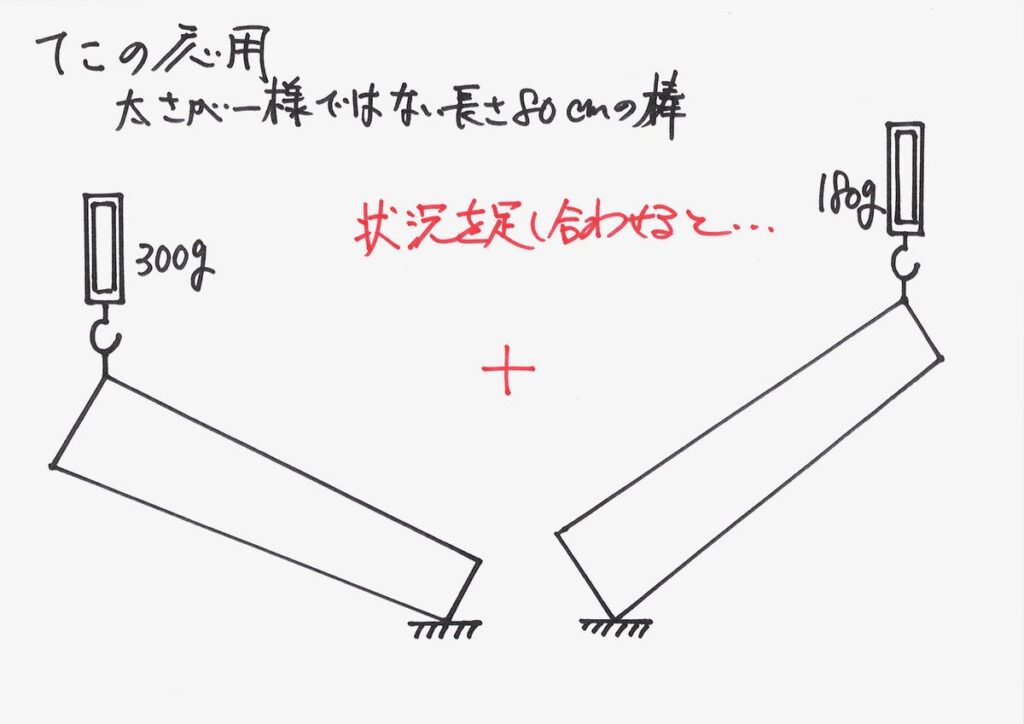
二つの状況を、足してみましょう。
上の片方ずつの重さを測った状況を「足し合わせて」みましょう。
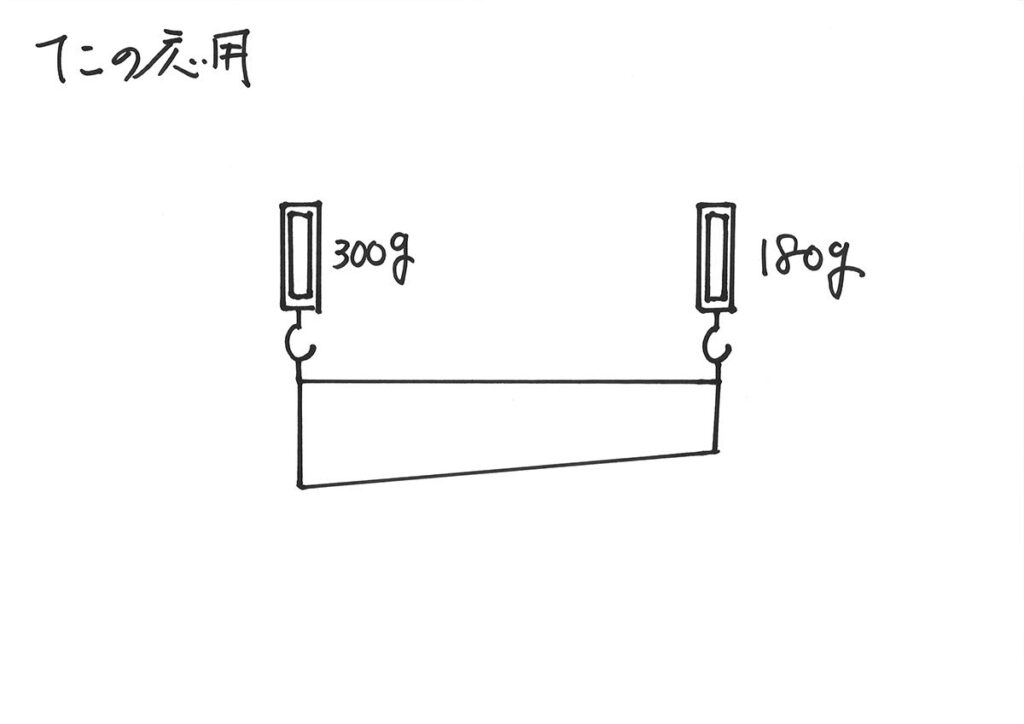
すると、上のように両側で、つり合います。
上の「棒の重さがない」時に、四つの点で考えた「つり合う」状況をイメージしましょう。
ここで、
男子小学生うん。
そうかも・・・
女子小学生ちょっと、しっくりこない気が
するけど・・・
上の「二つの現象・状況を足し合わせる」のは、少し難しいです。
この考え方は「重ね合わせの原理」とも言われますが、中学生〜高校生で習います。
男子小学生ちょっと
早いよね。
ここでは深追いせずに、「足し合わせたら、こんな感じになる気がする」くらいでも良いでしょう。
この「足し合わせる状況」をしっかりイメージできるのは、難しいです。
しっかりイメージ出来る方は、物理のセンスがあるかも知れません。
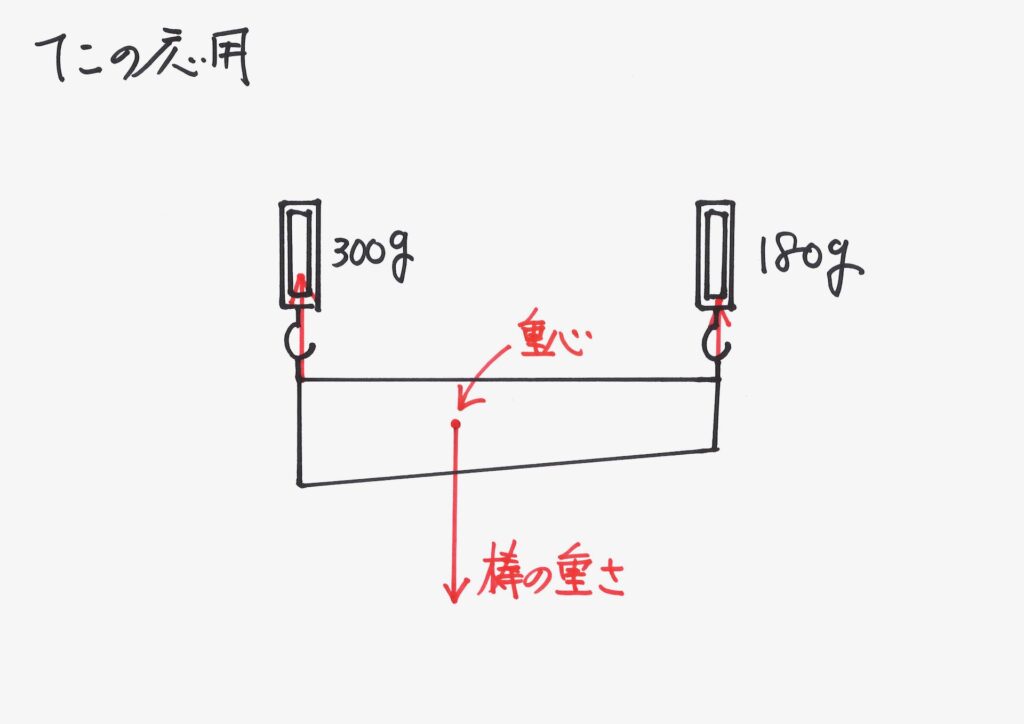
この「足し合わせた状況」を描いたら、「矢印で重さ・はかりが引っ張る力」を描いてみましょう。
図では、重心を示しています。
重心とは「モノの重さが一点に集まっていると考えられる」点です。
・モノ（棒など）の重さが一点に集まっていると考える点
・重心の位置は、モノ（棒など）の形によって変わる
・モノ（棒など）が、同じ太さ・密度（一様）であれば、重心は中心
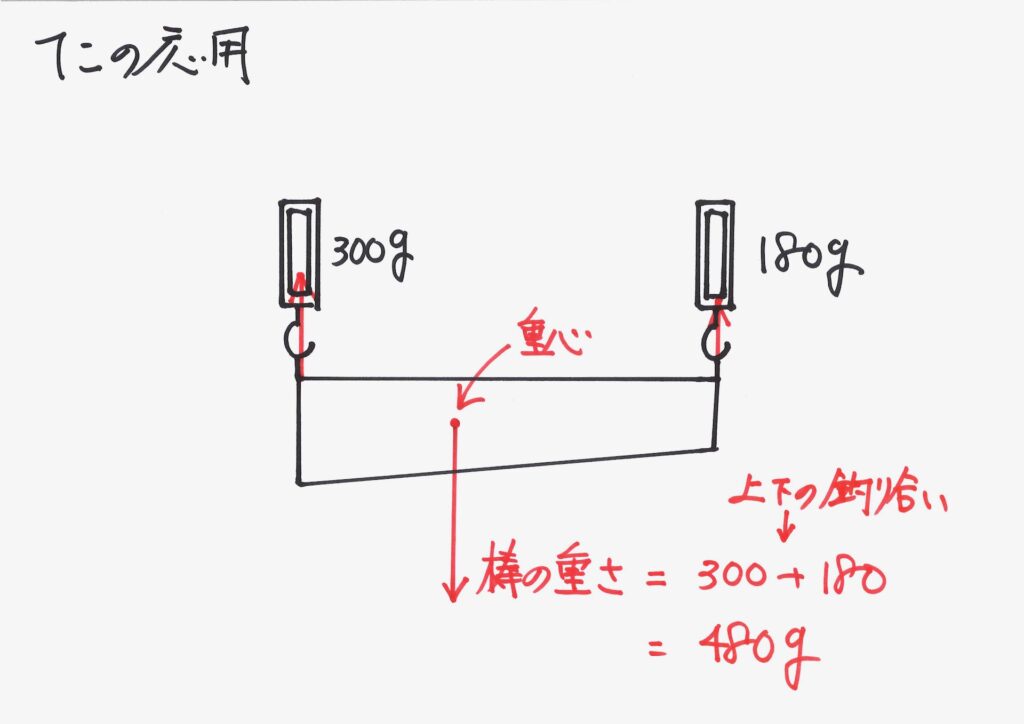
上と下で釣り合っているので、棒の重さが分かります。
男子小学生でもさ、
なぜ「重心に重さが集中する」の？
女子小学生確かに、
ちょっと不思議な感じ・・・
この「重心にモノの重さが集中」に関しては、しっかり理解するのは中学以降にしましょう。
小学生の間は、「モノの重さが集中する点が重心」という「決まり事」と考えましょう。
それでは、重心からの両端の距離を考えてみましょう。
長さが登場したので、「モーメント=回転する力」を考えてみましょう。
次回はモーメントを計算して、詳しく考えてみましょう。
次回は下記リンクです。
