前回は「図形・正六角形のポイント〜正六角形の性質・面積・対角線・問題4〜」の話でした。
問題4(再掲載)

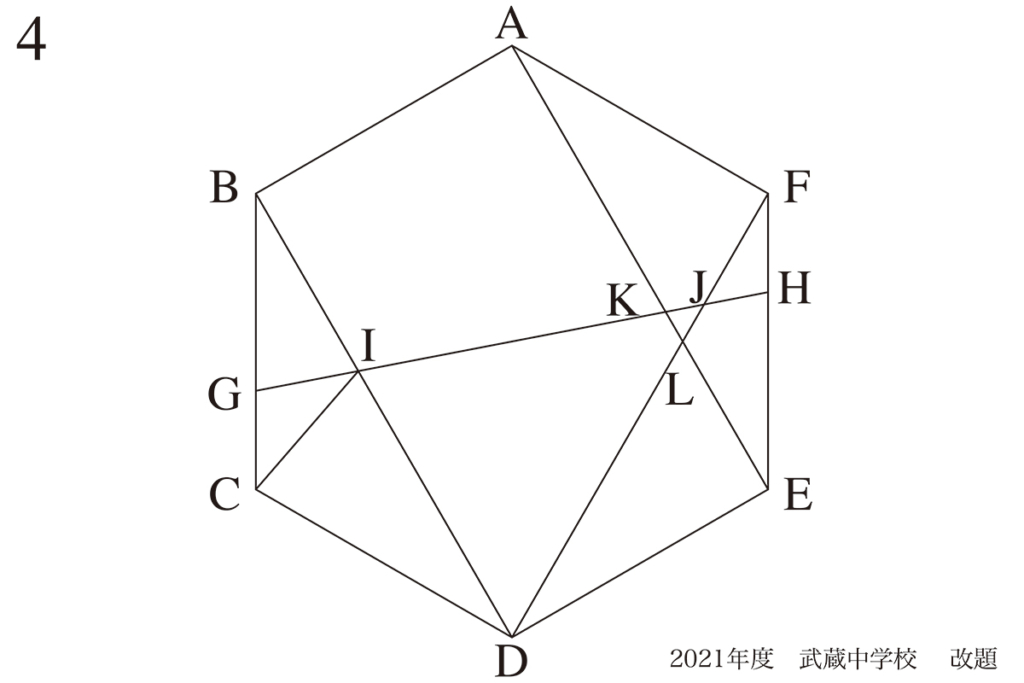
対称性のある図形の大事なポイント:中心・対称性・対称軸
まず(1)を考えましょう。
まずは問題文の比を書きながら、考えます。
正方形・正三角形など「正〜角形」のように対称性のある図形・円は、中心に注目しましょう。
そして、まずは中心を通る直線を引きましょう。
対称性のある図形で、中心と中心を通る直線(円の場合は直径)は非常に大事です。
本文ではADに線を引き、図形の中心Pを押さえます。
正六角形の対称性から、AB=BC=CD=DE=EF=FA=AP=PDです。
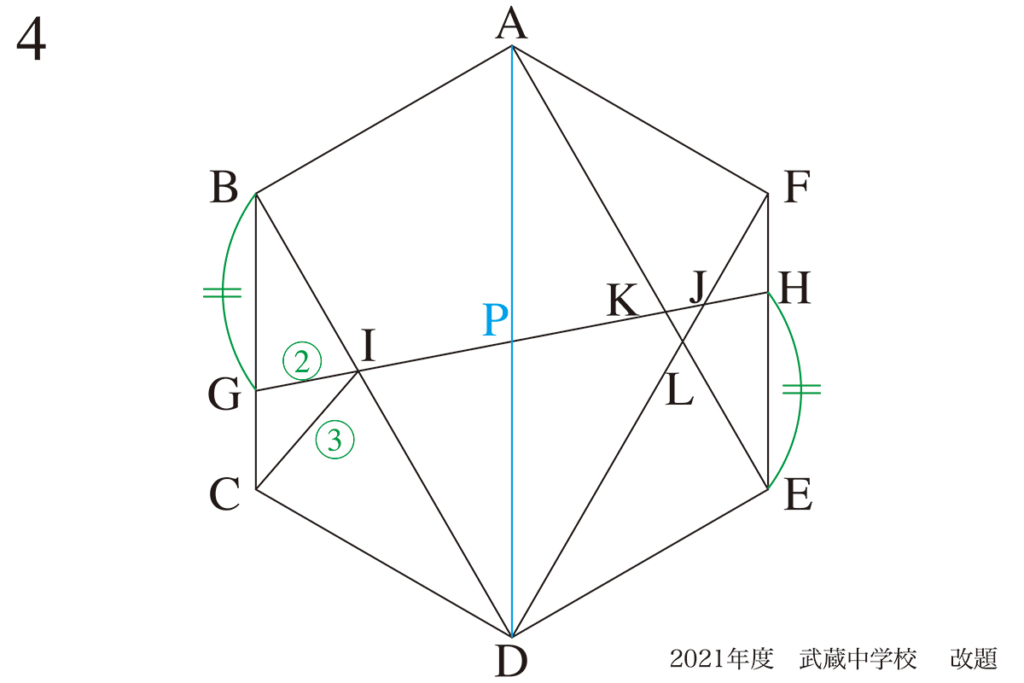
まず相似形を探す:平行な辺に着目
図形問題では、条件を図に描きこむことが大事です。
 男子小学生
男子小学生相似三角形は、
ないかな・・・
そして、相似形を探してみましょう。
そのためには、



平行な辺をまず
探そう!
平行な辺・線を探してみましょう。
平行な辺が多いので、相似三角形は沢山見つかります。
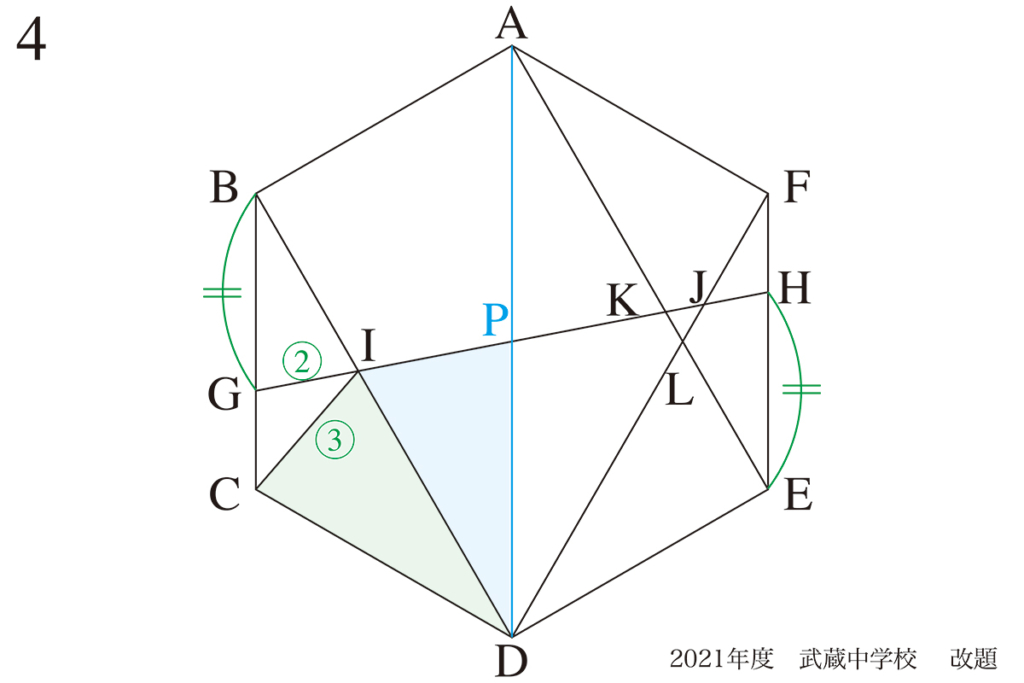
たくさん相似形が出てくる時は、相似三角形の中で特殊な場合=同じ(合同)三角形も探してみましょう。
下図の水色と緑の三角形は、CD=PD、ID共通、それらの辺が挟む角度が30度で同じです。
△CDIと△PDIは同じ(合同)です。(二辺挟角)
辺の長さの比と面積比
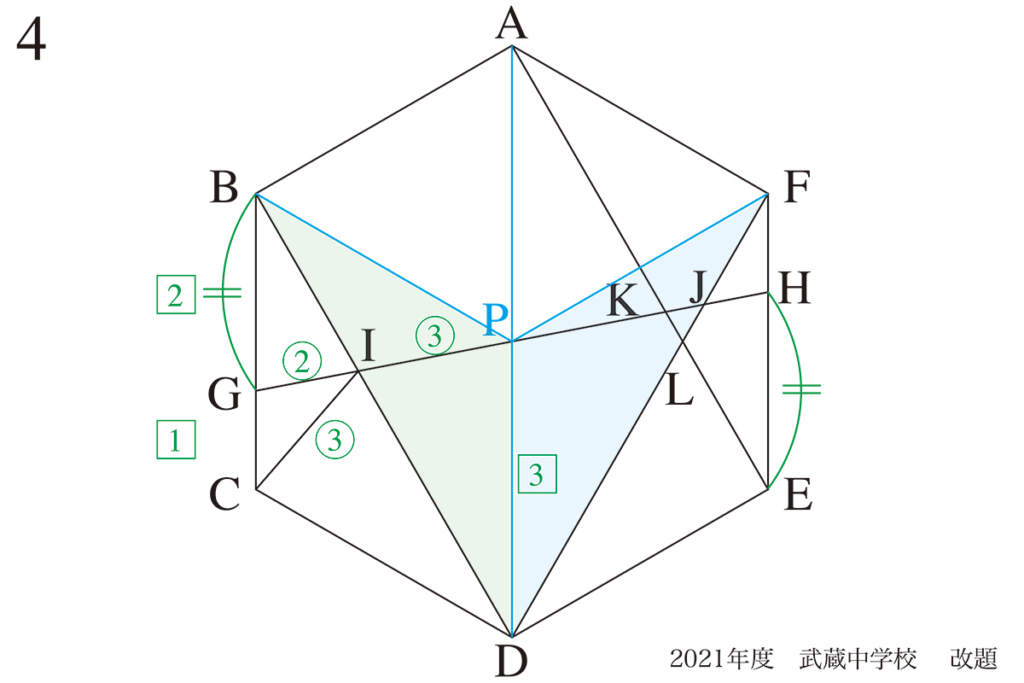

これで一気に「見えて」きます。
△BGIと△DPIは相似なので、BG : PD =2 : 3です。
上図の通り、様々な辺の比が分かります。
これらの「辺の比」などを「図形にどんどん描きこむ」ことが大事です。
あとは基本となる三角形の面積から、辺の比をもとに面積を求めます。
いくつか考えられますが、基準となる「分かりやすい図形」を考えましょう。
今回は、「基準となる図形」として、△BPD=△FPDを考えてみましょう。(上図の緑と水色)
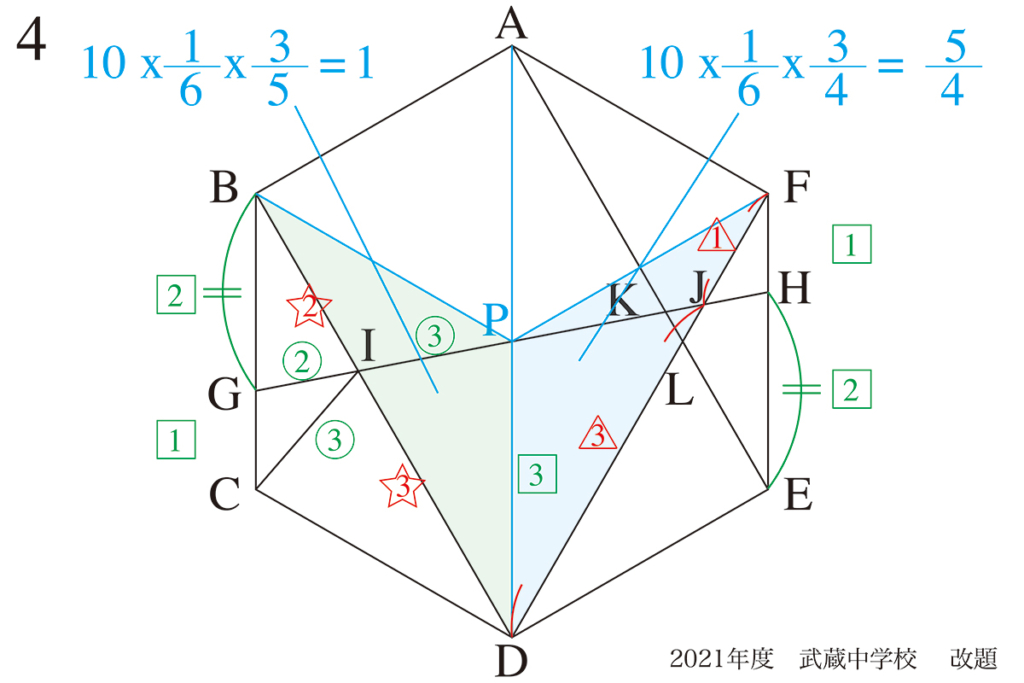

これらの三角形の面積は対称性から10×1/6なので、上の通りになります。
二つの三角形の面積を合計して、「答えは9/4」です。
9/4
(2)は、きちんと相似三角形と辺の比を考え、正確に解答を進めてゆく力が試されます。
次回は下記リンクです。


