前回は「図形問題の解き方・ポイント・コツ 3〜何に着目するか・一番良い解き方とは・自分の好きな考え方・視点を変える・図形を回転する・邪魔な線を消す・自分の視線を最優先・図形を描く・状況を整理する・大事なポイントに気づく〜」でした。
上手い補助線・良い補助線：自分でトライして勘を磨く
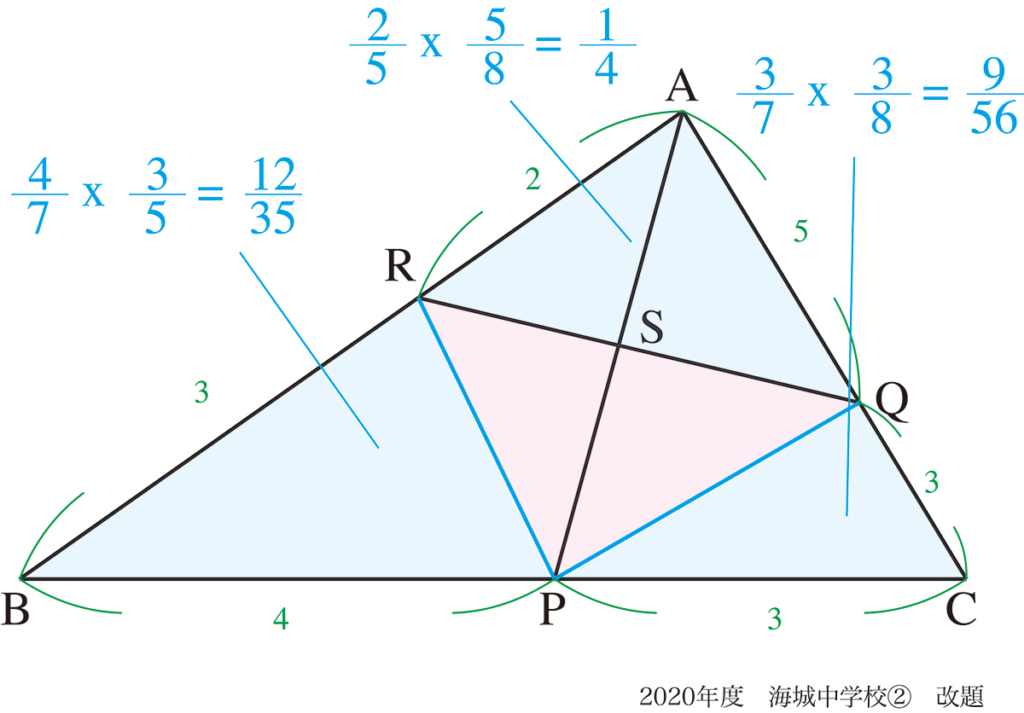
今回は、「上手い補助線・良い補助線の考え方」です。
補助線は、自分でいくつか試行錯誤すると、
これが
良さそうかな？
いや、
こっちの方が良いかな？
と勘が磨かれます。
この図形は、
この補助線が良い！
と教わると、
この補助線に
気づかないと、問題が解けないんだ・・・
と感じる方もいるかも知れません。
たいていの図形問題には、「解答に至る複数の補助線」があります。
それらの「補助線」の中には、「問題が解きやすい」や「早く解ける」などあります。
最も良いのは、同じ問題で「いくつかの補助線を試す」ことです。
実際に、自分の手で様々な補助線を引いてみると、
この補助線は、
〜だから、よさそう！
こっちの補助線は、
〜だから、ちょっと解きにくいかも・・・
と様々な気づきがあり、勘が磨かれます。
・多くの場合、「解答に至る複数の補助線」がある
・「問題が解きやすい」や「早く解ける」補助線がある
・同じ問題で「いくつかの補助線を試す」と勘が磨かれ、図形問題の力がアップする
補助線を考える姿勢：補助線によって何が変わるか？
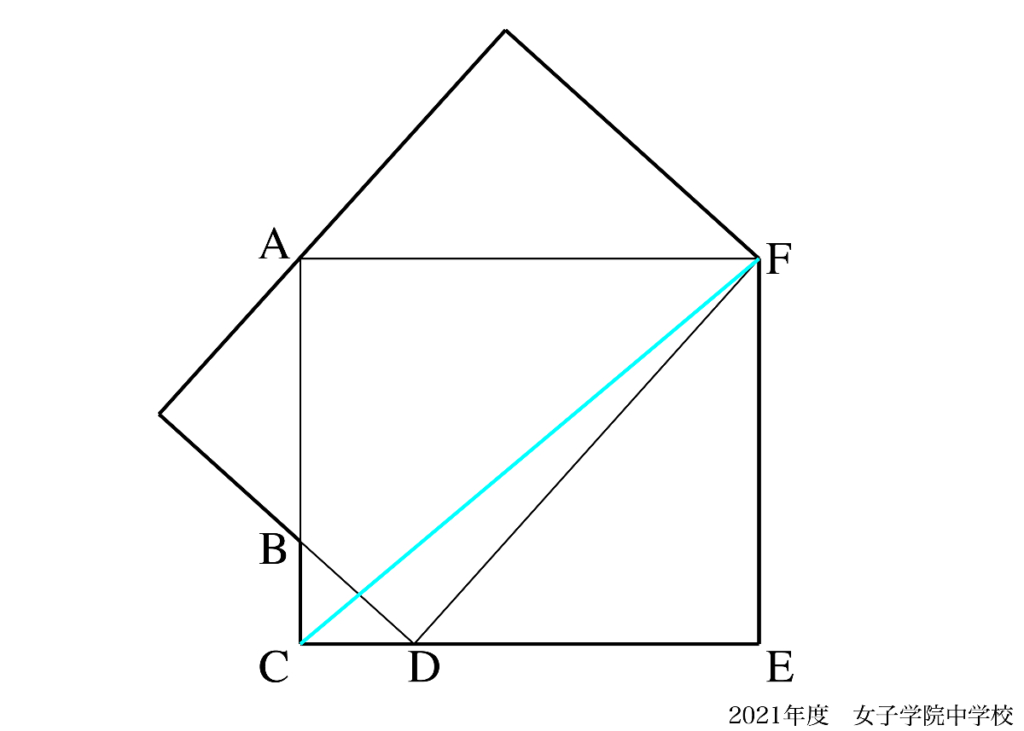
問題1の解法A,Bをご紹介しました。
ここで、解法Aの補助線に気づけると良いのですが、解法Bでも解ける話でした。
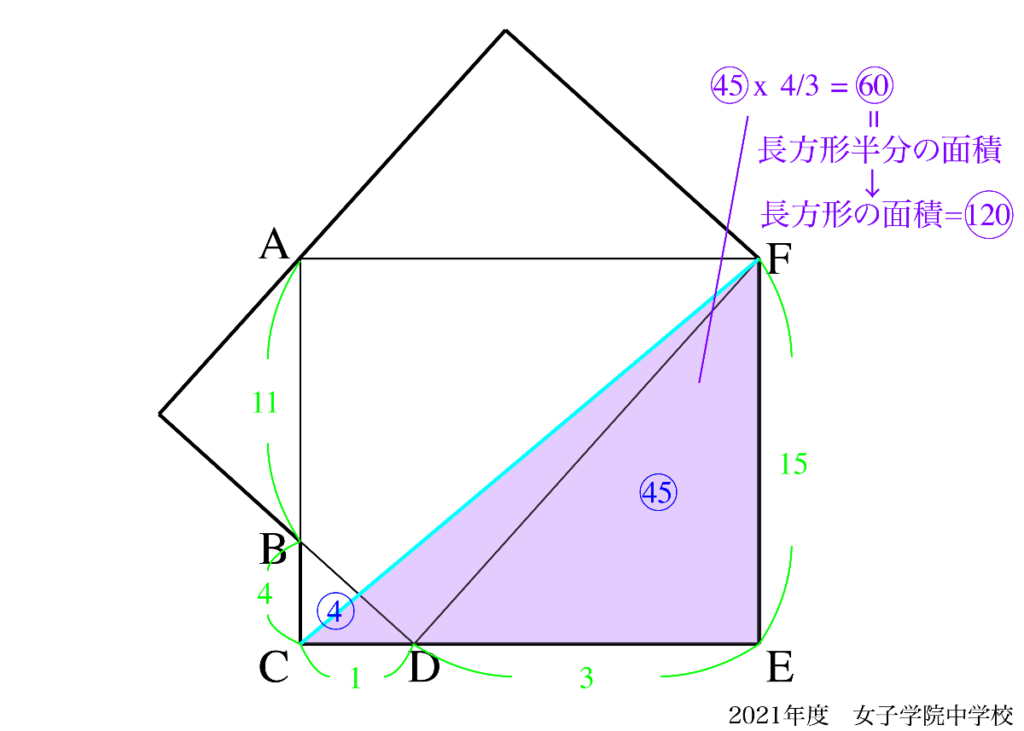
このように補助線はいくつか考えられます。
この補助線で
なければ、この問題は解けない！
という考え方は、持たないようにしましょう。
そうではなく、
他にも
解答に至る補助線はあるはず！
と考えましょう。
実際には「上手い補助線」「あまり上手くない補助線」はあります。
「どちらの補助線でも解ける」解法A,Bの二本の「別々の補助線」たち。
上記の解法A,Bの補助線で大きな違いを、少し考えてみましょう。
大きな違いは、解法Bの補助線だと「新たな交点が出てくる」ことです。
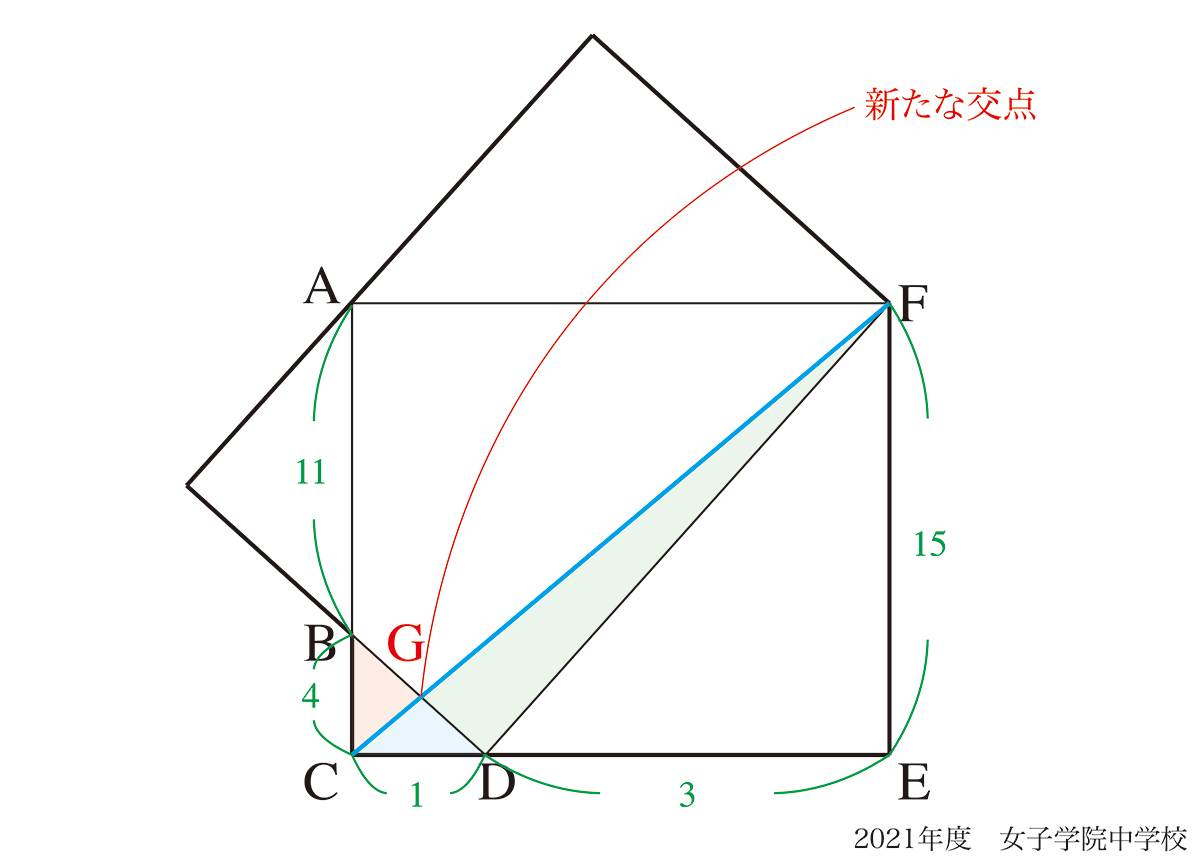
これは、少し考えにくくなります。
上図の通り、新たな交点Gが出てきて△BCD、△GCD、△GDFと3つの新たな三角形が出てきます。
新たな交点が出てくると、図形が分割されて、考えにくくなる場合があります。
「意図的に図形を分割して、解きやすくする」場合もあるので、問題によります。
考えた補助線で新たな交点が出てきたら、
この補助線は、
あまり上手くないかな・・・
と考えるのは、一つの考え方として良さそうです。
新たな交点が登場する場合：図形の中と外
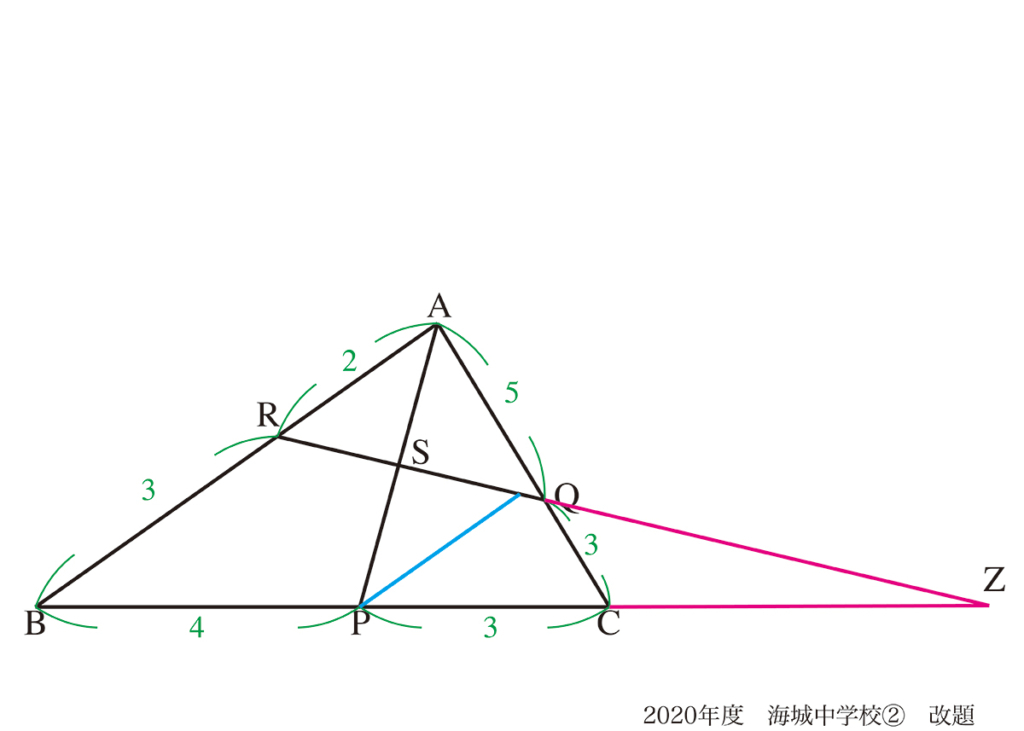
問題2で「自分で図形の外の世界へ飛び出す」話をしました。
この時の補助線は「外に飛び出して、新しい交点Zが発生」しています。
新しい交点が
登場しているから、あまり良くないのかな？
問題2の新たな交点Zと、問題1の新たな交点Gには大きな違いがあります。
それは、「もともとある図形を分けているかどうか」です。
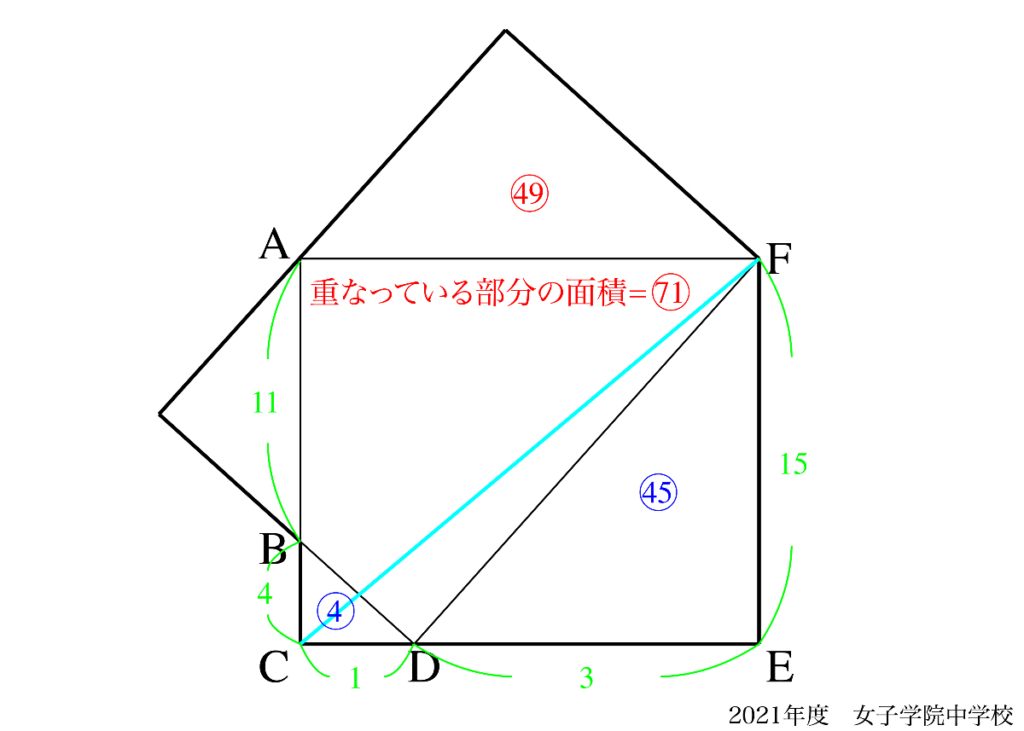
問題1の交点Gは問題の図形を分けているので、考えにくくなるのです。
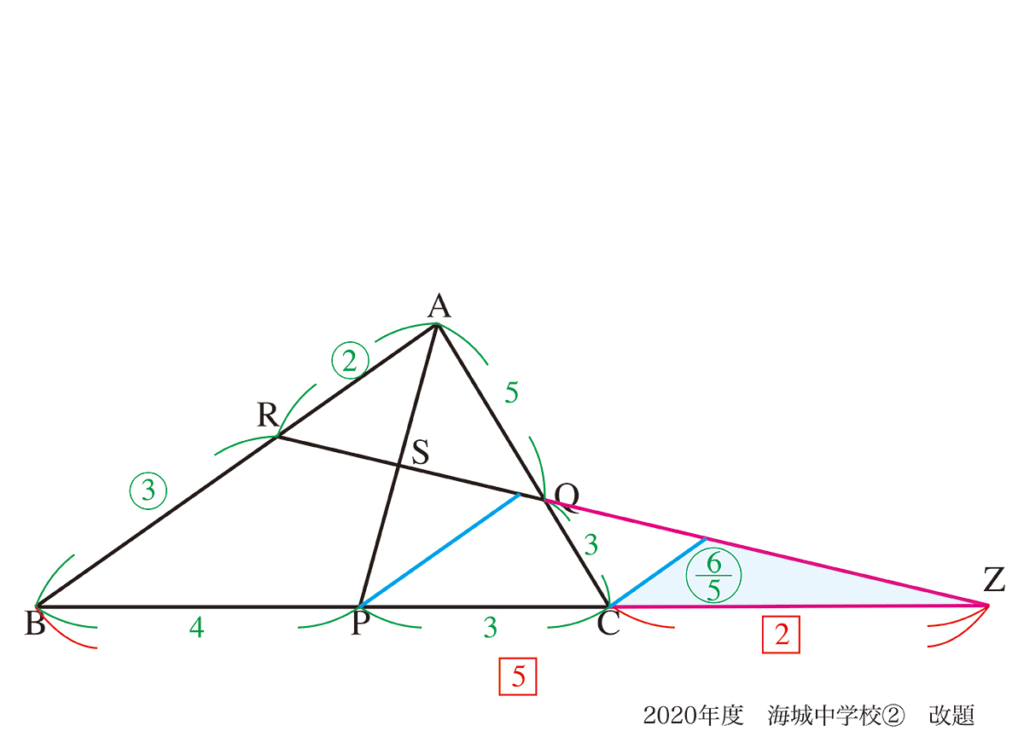
問題2の交点Zは、「自分で新たに作成した図形」ですから、考えにくくなることはなさそうです。
図形問題を考えるとき、「補助線によって、新たな交点が出来るか」を考えてみましょう。
・補助線によって「新たな交点」が出てくるかどうか
・「新たな交点」が登場する場合、もとの図形の中か外のどちらか
このように「ただ解くために補助線引く」よりも「補助線を少し考えてみる」ようにしましょう。
この補助線は、
このあたりが良さそうだ！
補助線の効果や「良い・良くない」は、あります。
一方で、それらは「主観であり、それぞれの方の意見」でもあることが多いです。
様々な視点から眺めてみる姿勢を身につけること。
すると、図形問題の学力が、さらに大きく上がるでしょう。
そして、その「様々な視点から考える」姿勢は、算数・数学の学力アップに大いに役立ちます。
