前回は「直角二等辺三角形の辺の長さの求め方〜図形を分割・「直角二等辺三角形が次々と生まれる」性質・直角二等辺三角形の「斜辺しか分からない」とき・問題 11(3)解法A〜」の話でした。
問題11(3)(再掲載)
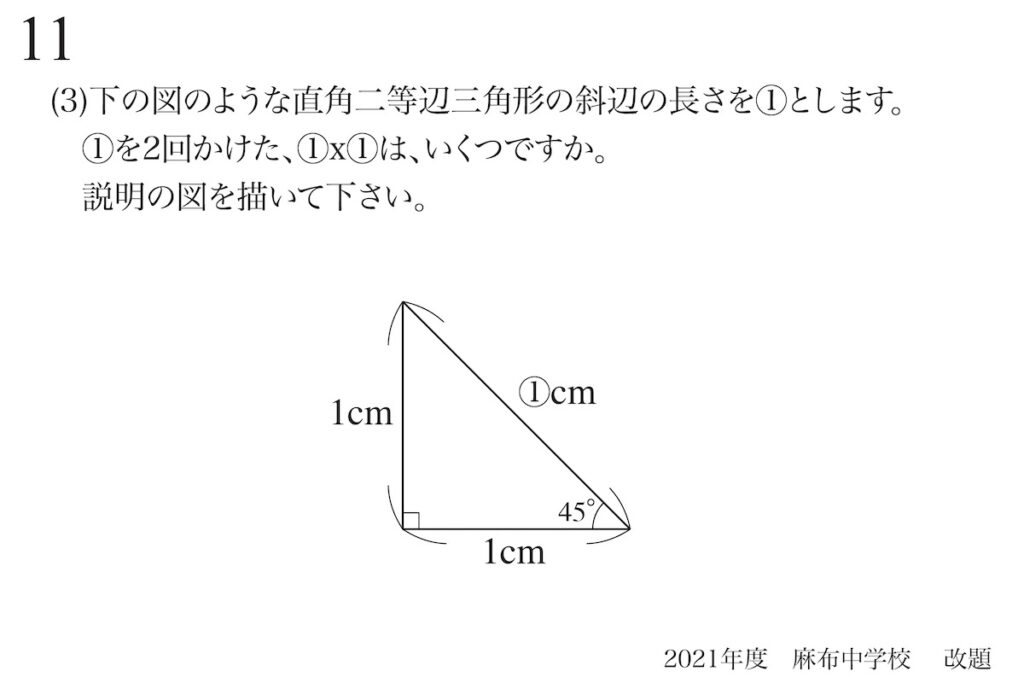
図形の外に直角二等辺三角形を展開
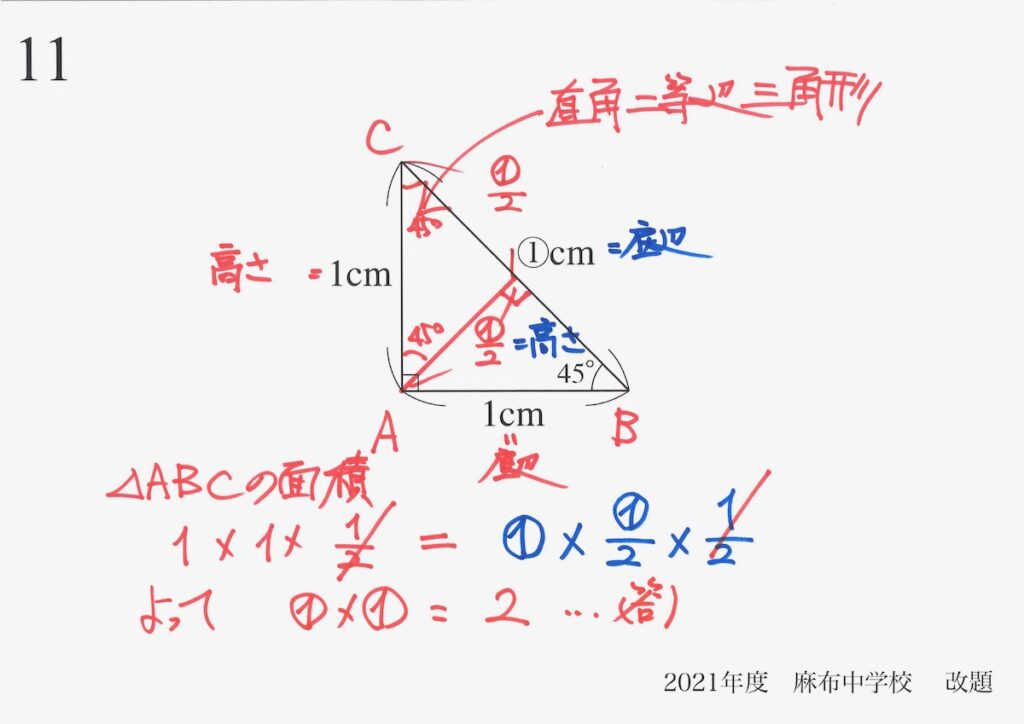
解法Aでは、与えられた図形の中で補助線を引いて考えました。
直角二等辺三角形の中に「新たに直角二等辺三角形が出来る」性質から考えました。
「与えられた図形の中」は、図形を分解・分析するような基本的な考え方です。
「図形の中に補助線をひく」のは、「図形を分けて、図形の性質を調べる」イメージです。
今回は、図形の外に出てみましょう。
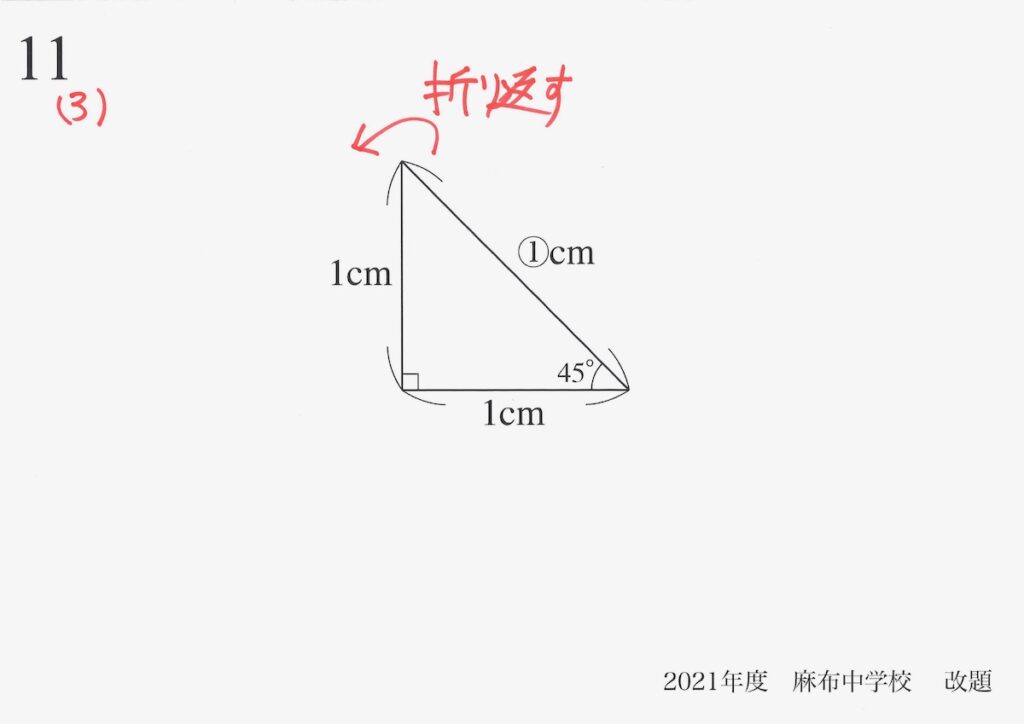
図形の外に出て考えるのは、下記の考え方が基本になります。
・線を延長して、平行な直線と組み合わせて相似形を作る
・図形を折り返して、同じ図形をもう一つ作成
いわば、直角二等辺三角形を「外部に展開してゆく」イメージです。
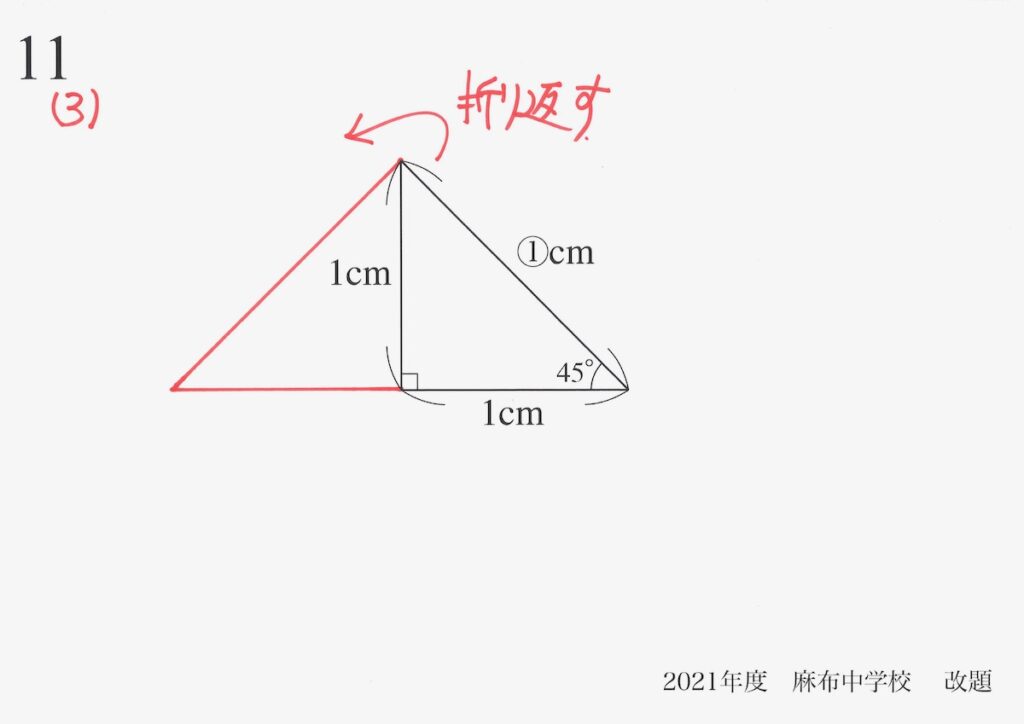
直角二等辺三角形を折り返して、もう一つ作成しましょう。
折り返すと、「元の図形の2倍の大きさ」の図形が出てきます。
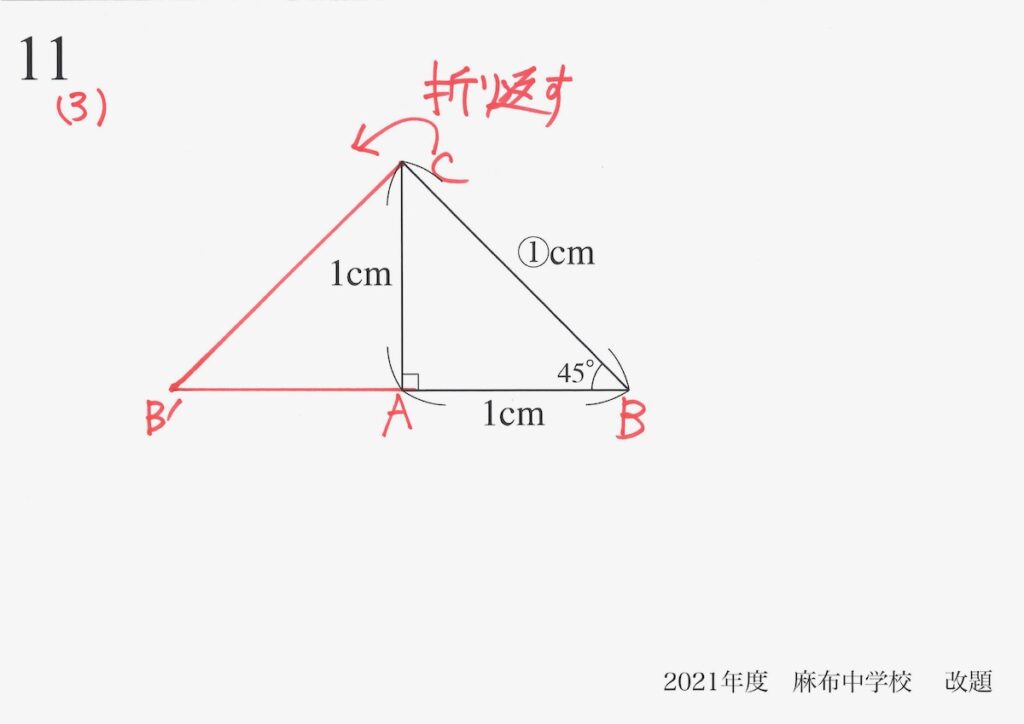
この図形の特徴を、考えてみましょう。
元の頂点をA,B,Cとすると、折り返した点はB’と考えましょう。
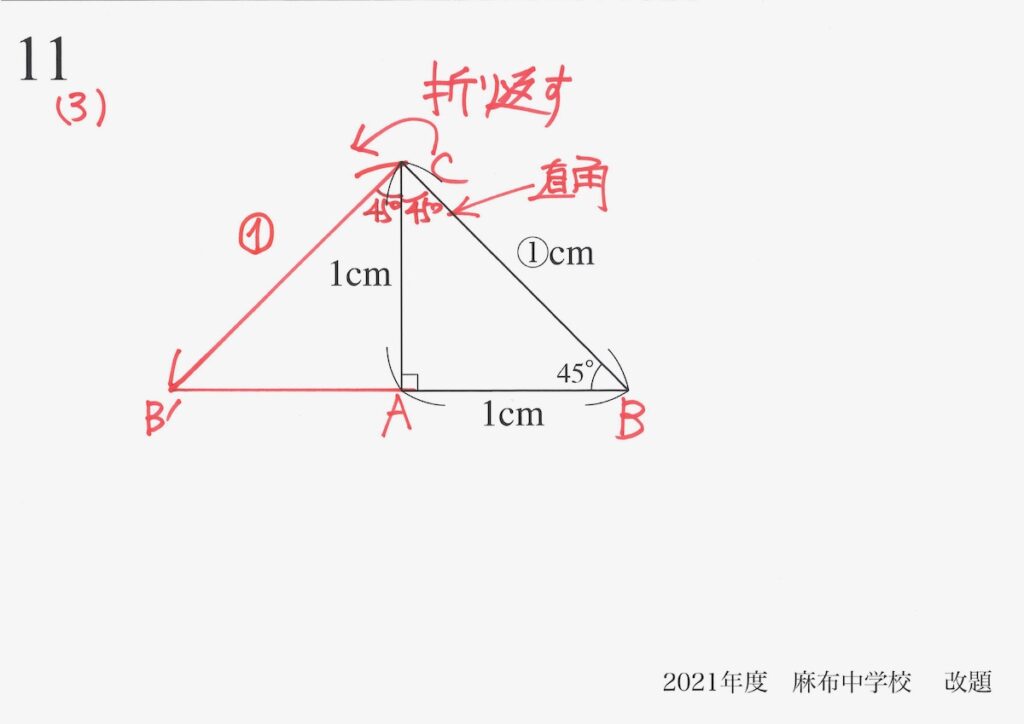
BとB’は、ACを軸に関して「対称な関係」なので、角度や長さが分かります。
「折り返す」時は、「同じ角度・長さ」が分かったら、どんどん描いていきましょう。
実際に手を動かして描いてゆくと、様々な特徴・性質が分かります。
図を描いて学ぶ話を、上記リンクでご紹介しています。
直角二等辺三角形の特徴と性質

45°がたくさん見えてくると、角Cが45+45=90°(直角)と分かります。
そして、折り返したので「ABとAB’は同じ長さ」です。
そこで、新たにできた三角形B’CBは、直角二等辺三角形です。
 女子小学生
女子小学生また、直角二等辺三角形が
出てきたね!
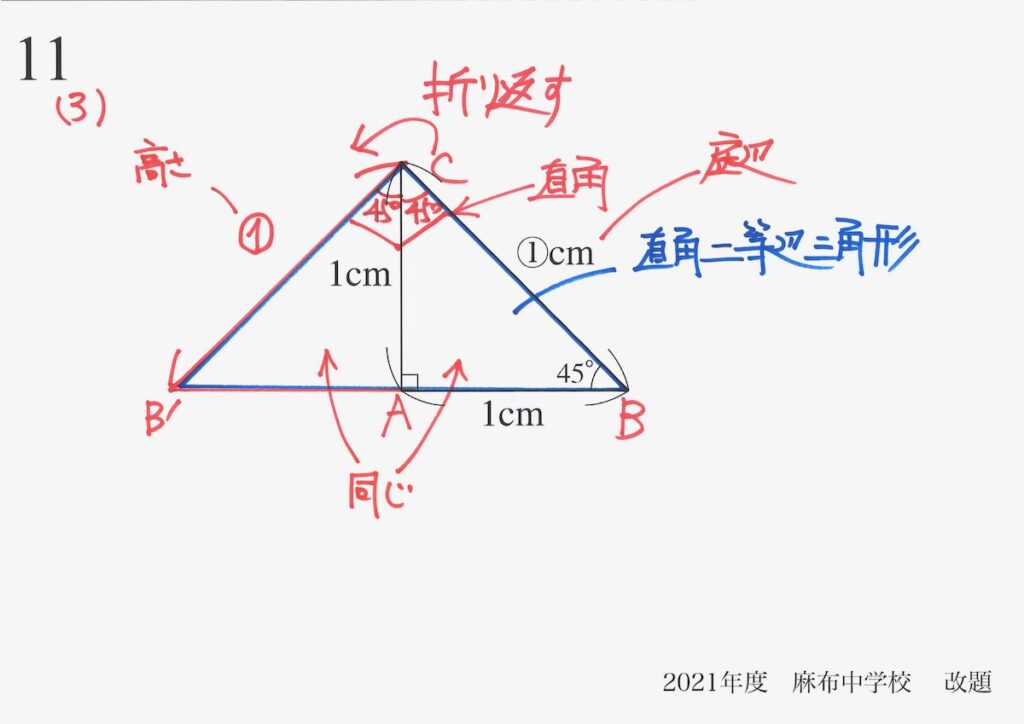

これで、前回と同じように「面積を2通りで考える」をやってみましょう。
・図形の形を三角形・四角形に分割
・底辺と斜辺の見方を変えて、面積を計算
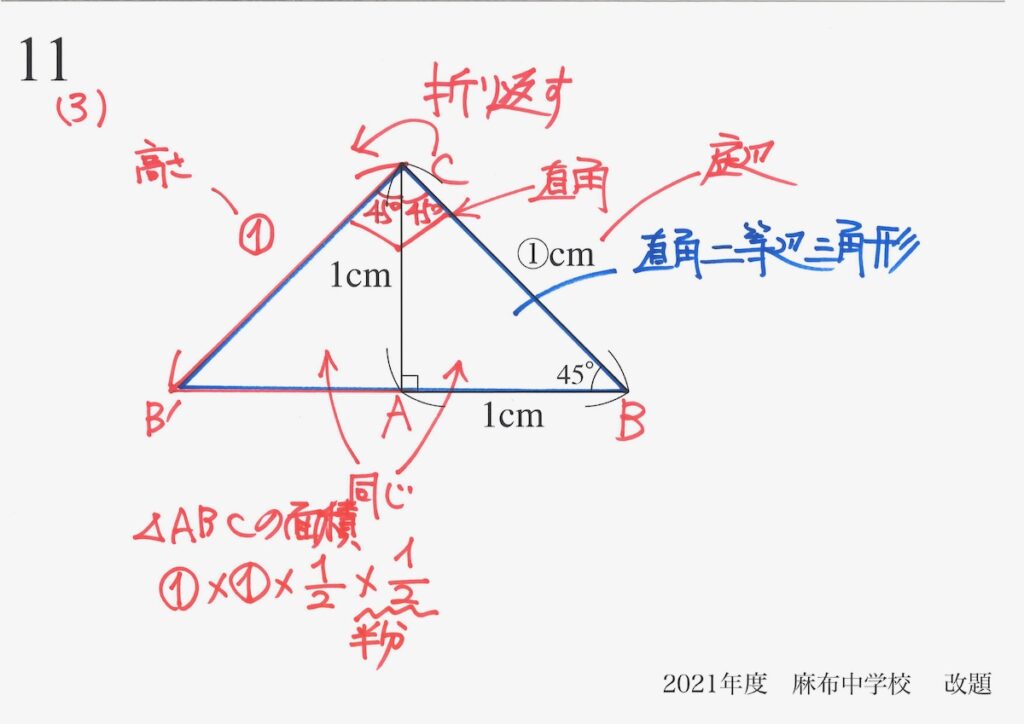

「赤色の底辺・高さ」で△ABCの面積を計算します。
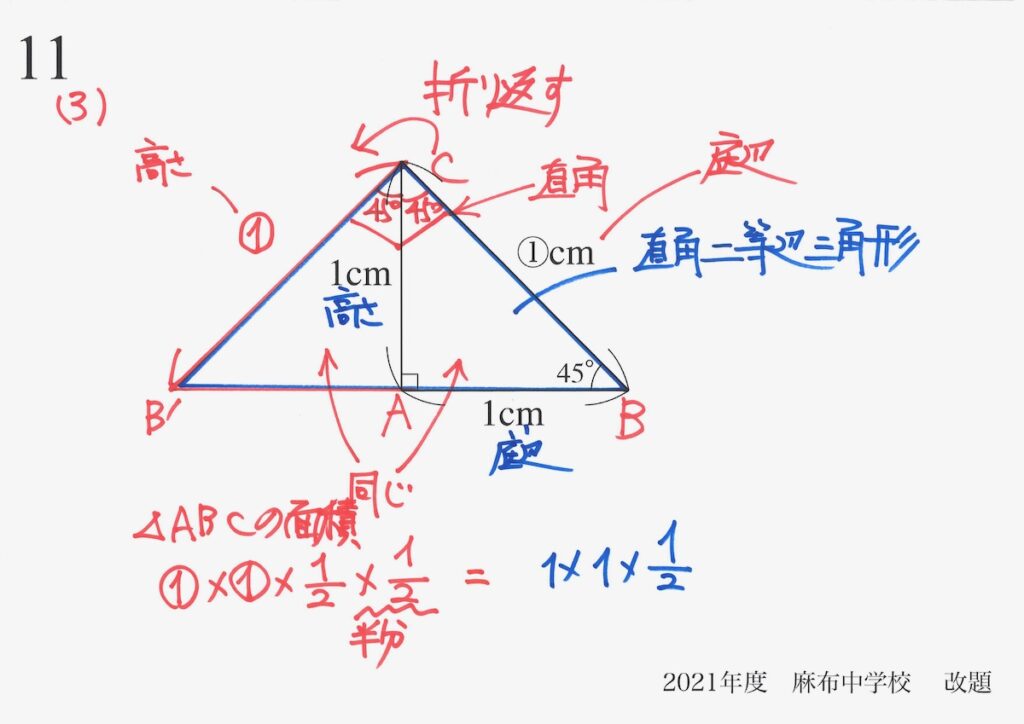

そして、「青色の底辺・高さ」で△ABCの面積を計算します。
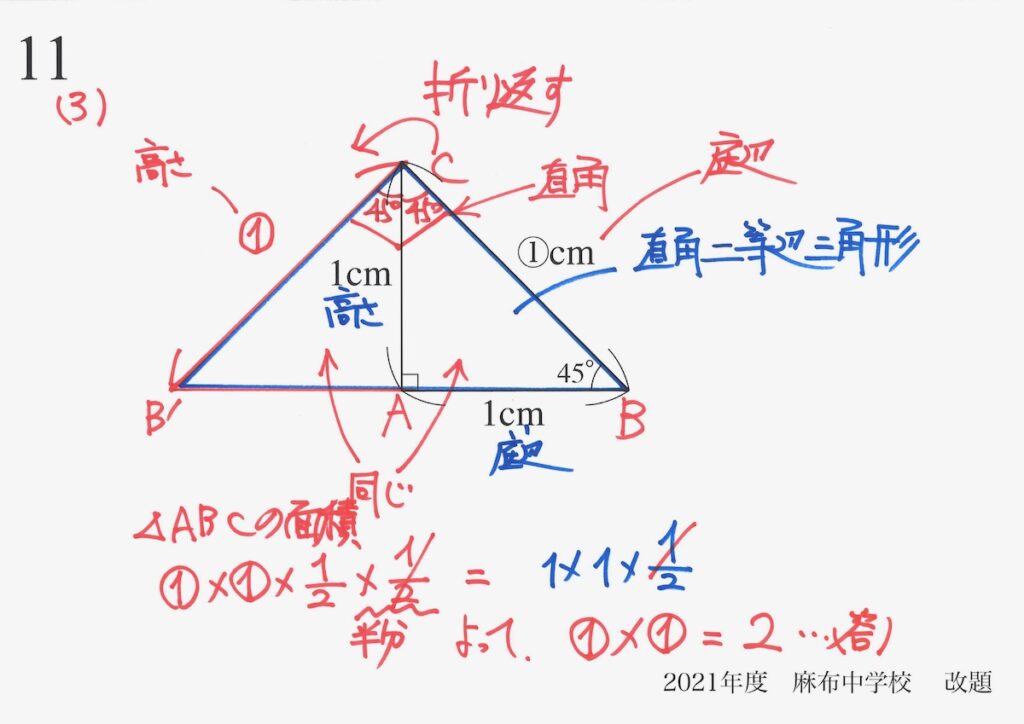

これらが等しいので、解法Aと同じことが答えになりました。
・①x①=2
直角二等辺三角形の「斜辺しか分からない」とき:正方形をつくる
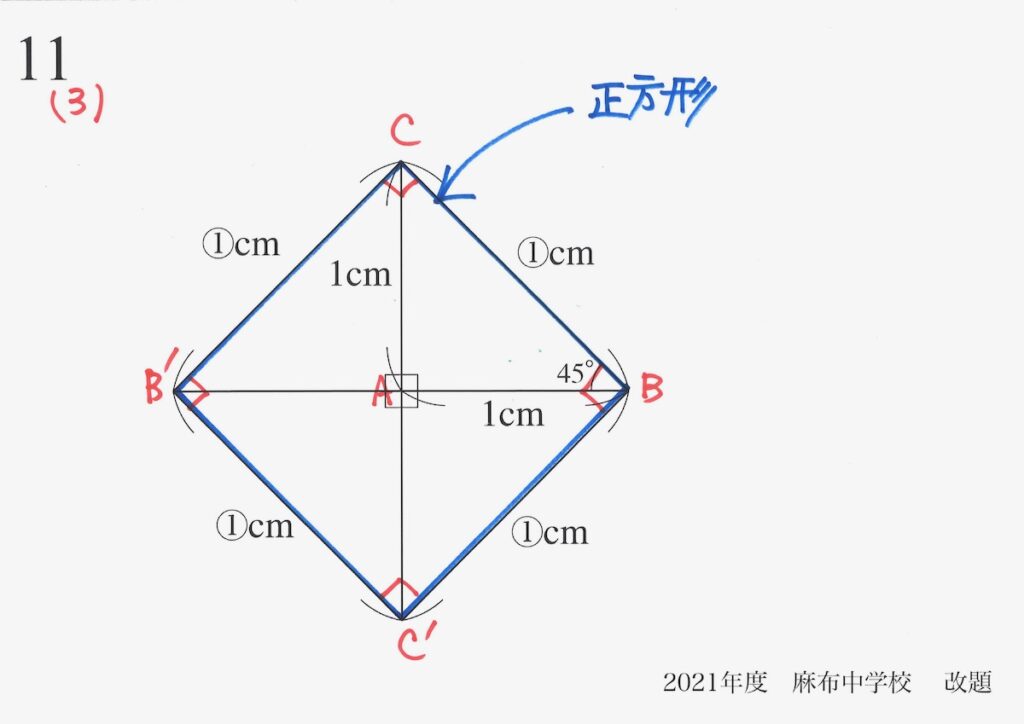

もう一度折り返してみましょう。
すると、どういう図形が見えてくるでしょうか。
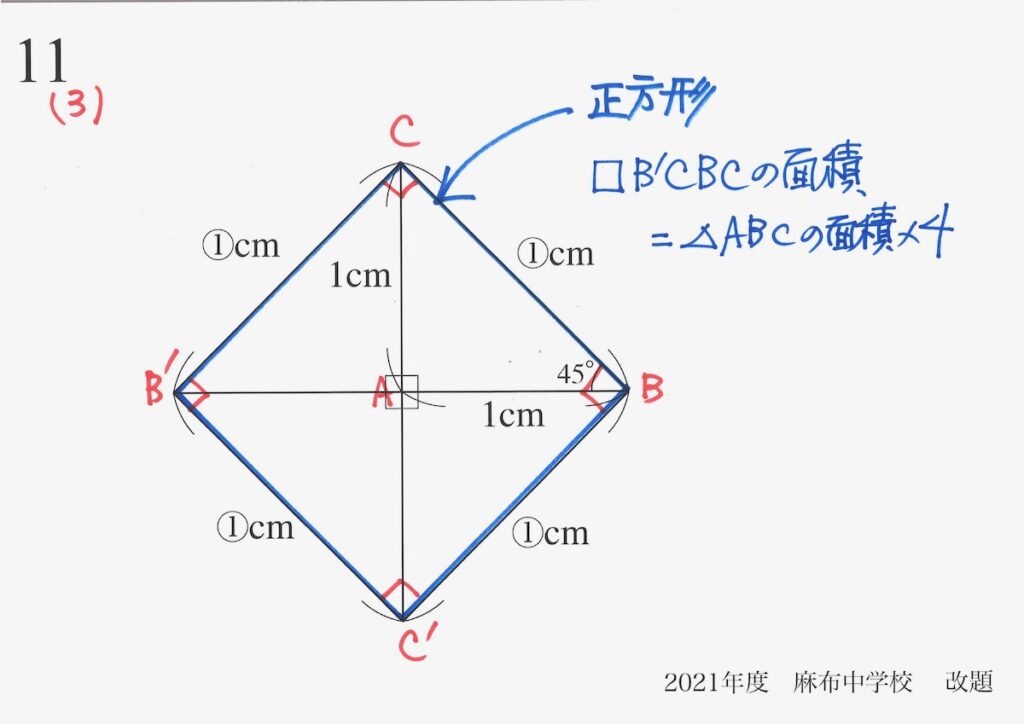

新しい図形「B’CBC’は正方形」となります。
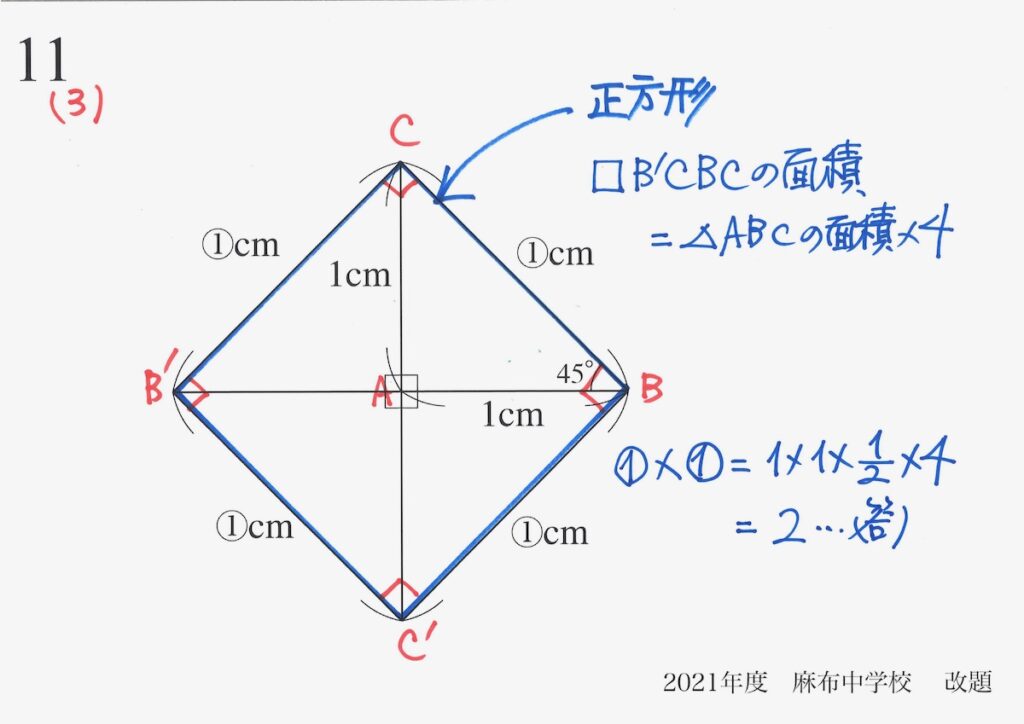

そして、この正方形の面積は、元の直角二等辺三角形の4倍です。
解法Bと似ていますが、この関係からも考えることが出来ます。
直角二等辺三角形を折り返して展開してゆくと、さらに直角二等辺三角形となりました。
・直角を挟む辺の長さが同じ三角形
・直角以外の角度は45度(直角の半分)の三角形
そして、もう一度折り返して展開すると、最後に正方形となりました。
・全ての辺の長さが同じ三角形
・全ての角度が等しい(60度)三角形
これで、「直角二等辺三角形の斜辺の長さしか分からない時」の考え方が分かりました。
「斜辺x斜辺」を考えると、正方形の面積となります。



これで、「直角二等辺三角形の斜辺しか分からない」時も
バッチリだね!



折り返して、直角二等辺三角形や
正方形が出来るのは、不思議な感じだね!
正方形は、最も特徴的な図形です。
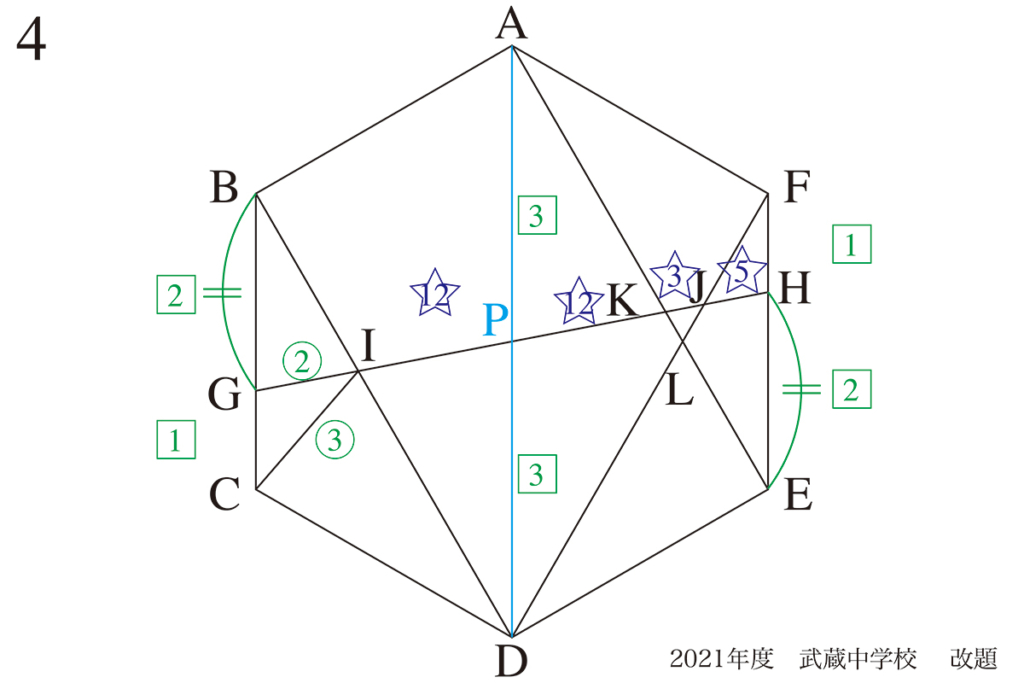
正六角形や「正〜角形」の問題の解き方を、上記リンクでご紹介しています。
それらの図形を分解してゆくと、二等辺三角形や正三角形が現れます。
「図形を展開したり、分解したりする考え方」がしっかり出来ると、大抵の平面図形は解けるようになります。
(4)の解法は次回ご紹介で、下記リンクです。




