前回は「図形の性質を理解と解き方〜直角二等辺三角形の性質・正方形と直角二等辺三角形・図形の性質と最大・最小の面積・問題11(3)(4)(5)〜」の話でした。
問題11(3)(再掲載)
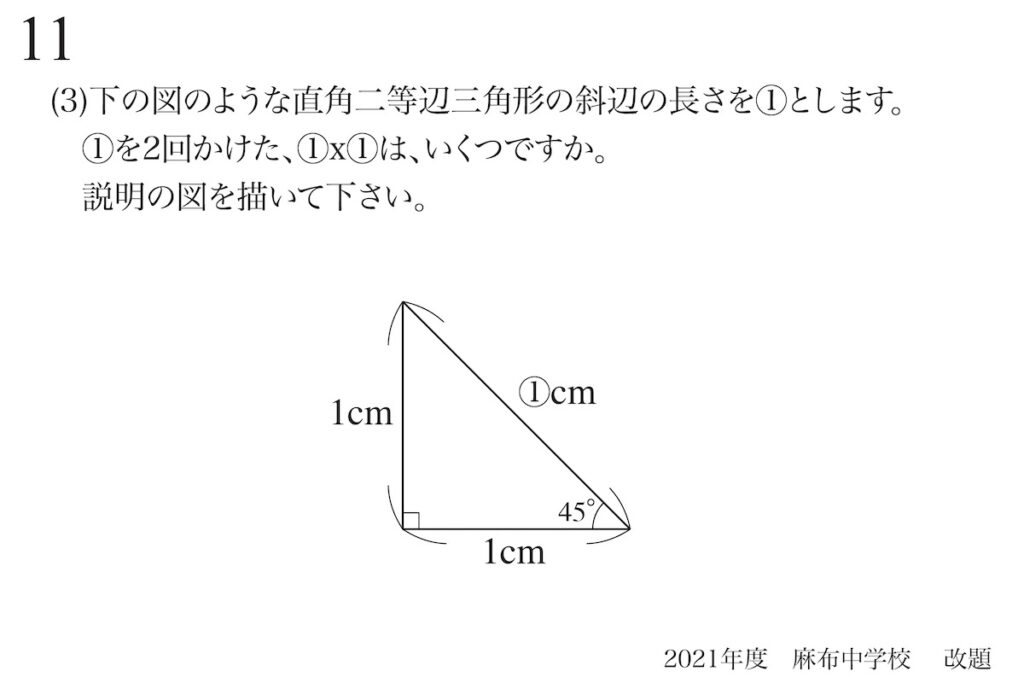
直角二等辺三角形の辺の長さ
基本的な図形は、三角形と四角形です。
特殊な四角形は長方形で、さらに「全ての辺の長さが等しい」のが正方形で「かなり特殊」です。
・全ての辺が同じ長さの四角形
・全ての角が同じで直角の四角形
三角形の中で特殊なのは、二等辺三角形と直角三角形、そして正三角形です。
正三角形は「全ての辺の長さが等しい」と「全ての角度が等しい(60度)」非常に特殊な三角形です。
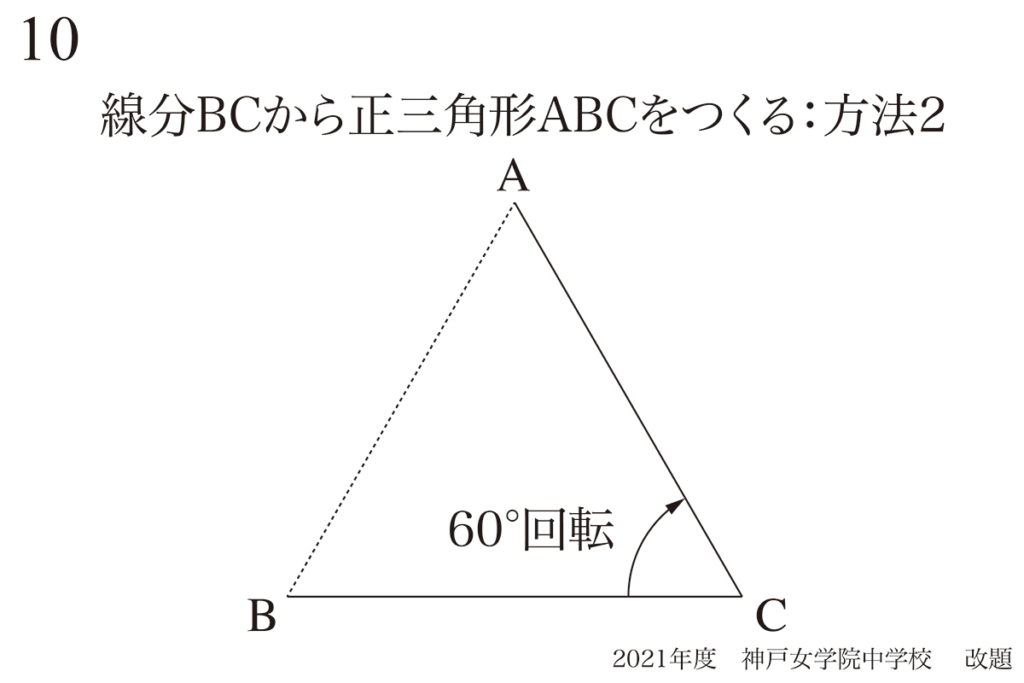
「全ての辺の長さが等しい」と正三角形になり、「全ての角度が等しい(60度)」と正三角形になります。
・全ての辺の長さが同じ三角形
・全ての角度が等しい(60度)三角形
この条件は「どちらかを満たすと正三角形」となります。
この性質は大切なので、しっかり押さえておきましょう。
・直角を挟む辺の長さが同じ三角形
・直角以外の角度は45度(直角の半分)の三角形
二等辺三角形と直角三角形は別の条件です。
「二等辺三角形だけど、直角三角形ではない」三角形はたくさんあります。
「直角三角形だけど、二等辺三角形ではない」三角形もたくさんあります。
その中、「直角二等辺三角形」は非常に特殊です。

 男子小学生
男子小学生三角定規の
片方だよね!
皆さんが三角定規をつかっているので、馴染みがあると思います。
ところが、直角二等辺三角形の斜辺の長さは「算数では分からない」長さです。
そのため、直角二等辺三角形の「斜辺しか分からない」図形問題は、難問になる傾向があります。
図形を分割:「直角二等辺三角形が次々と生まれる」性質
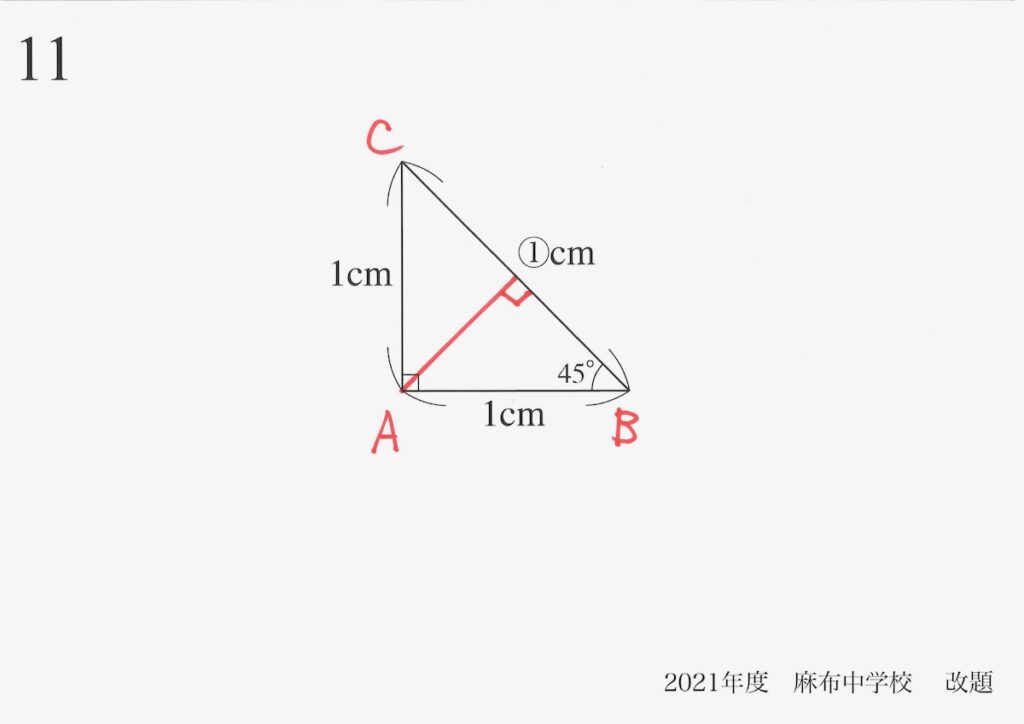

直角二等辺三角形は、正三角形と同様に「特殊な三角形」です。
直角二等辺三角形からは、「直角二等辺三角形が次々と生まれる」性質があります。
直角二等辺三角形の頂点にA,B,Cと名前をつけて、Aから辺BCに垂線(BCに垂直な直線)を引きます。
すると、どのような三角形が出てくるか、考えてみましょう。
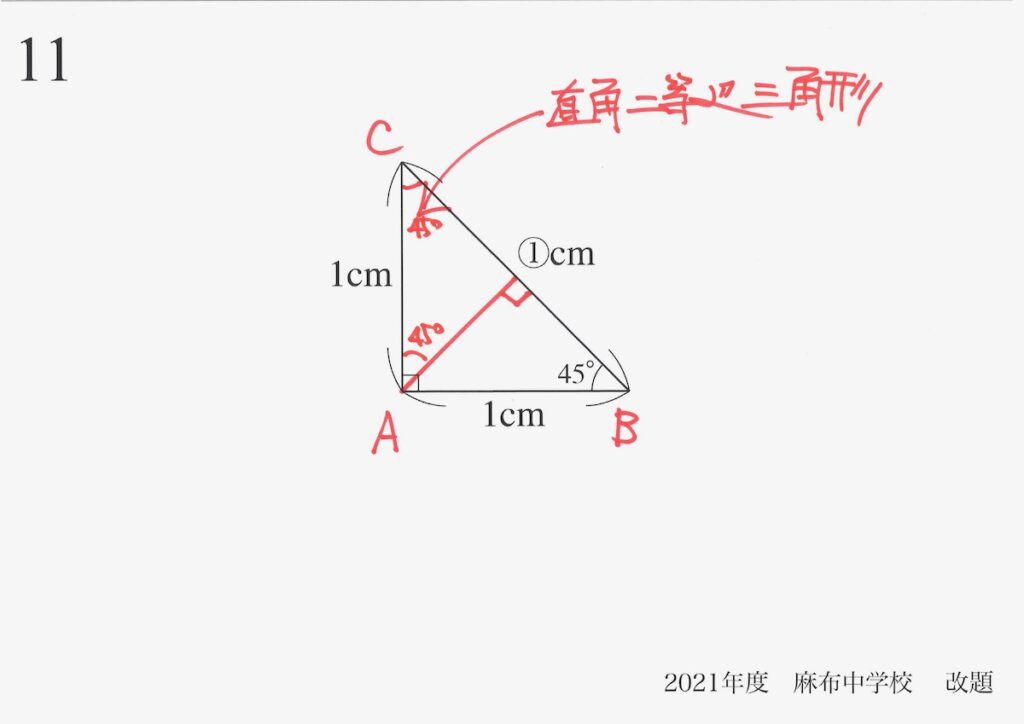

二つに等しく分割された三角形は、両方が直角二等辺三角形になります。
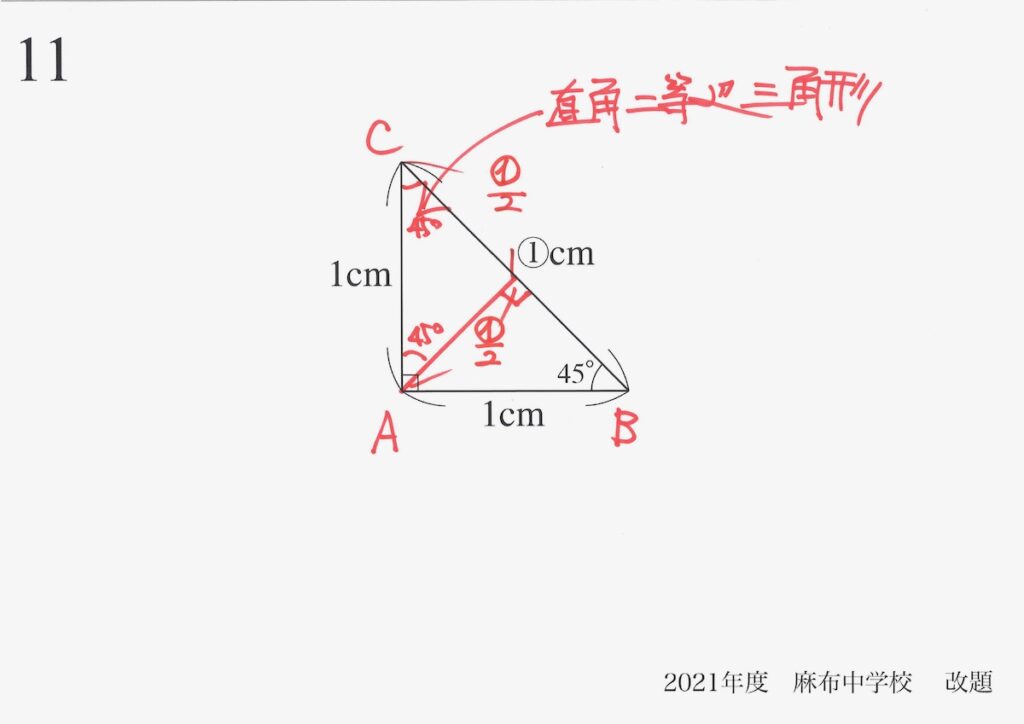

直角二等辺三角形は、「直角を挟む辺の長さが同じ」なので先ほど引いた垂線の長さが分かります。
直角二等辺三角形ABCの面積を、二通りの方法で表してみましょう。
底辺と高さを考えると、
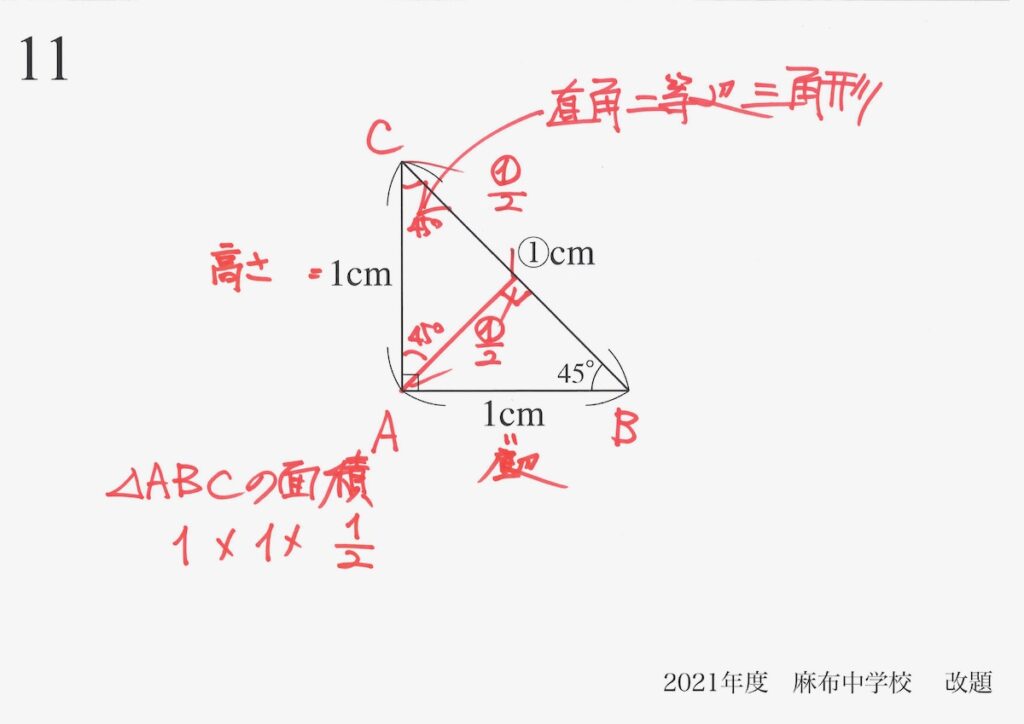

赤色の「底辺・高さ」で考えて、△ABCの面積が求まります。
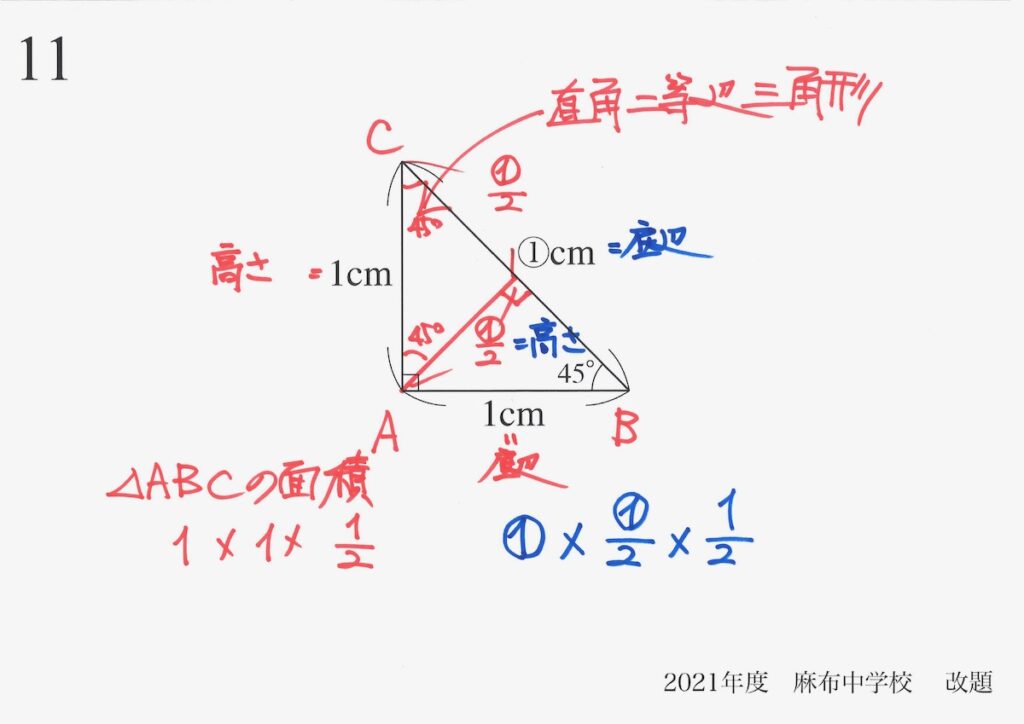

青色の「底辺・高さ」で考えて、△ABCの面積が求まります。
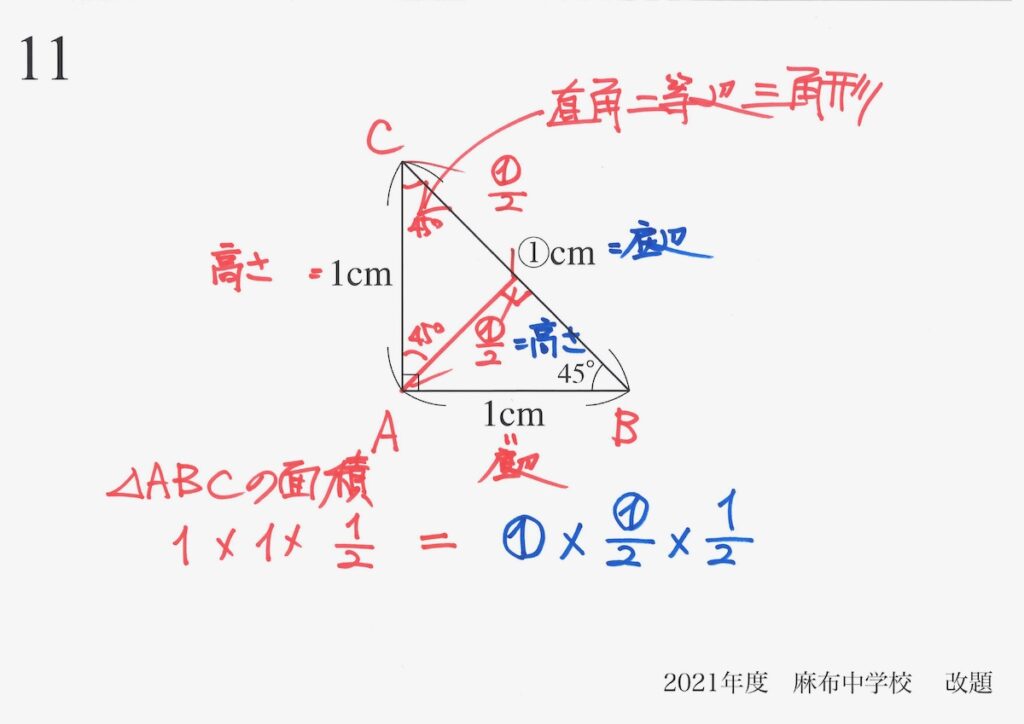

考え方は異なっていても、「面積は同じ」ですから、二つの式は等しいはずです。
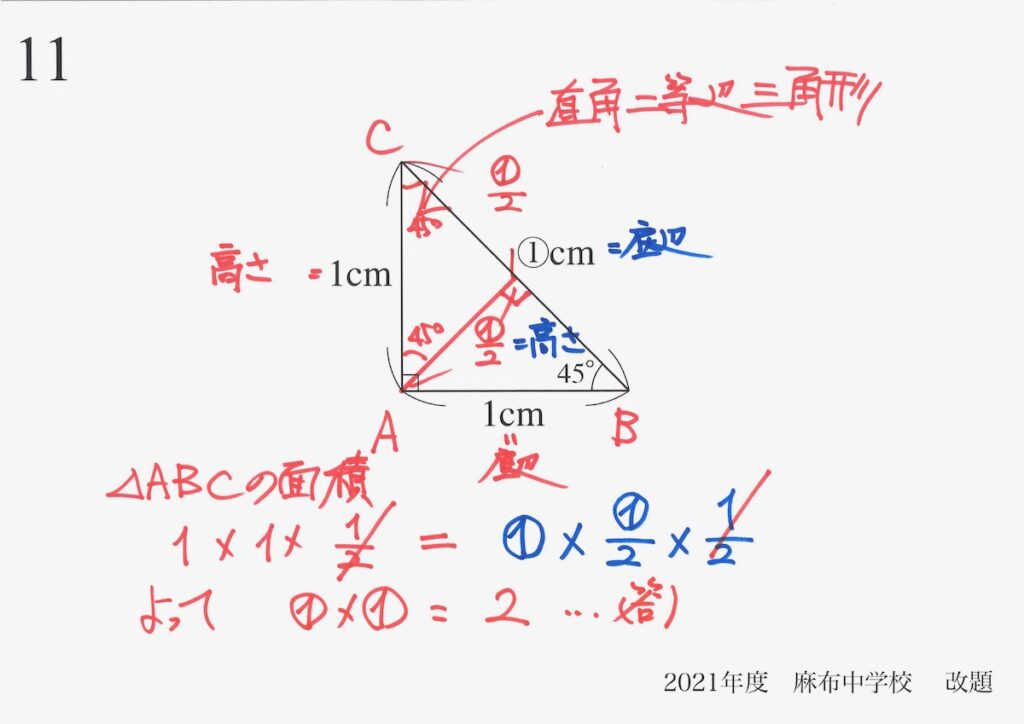

これで、両辺を比較すると答えが求まります。
・図形の形を三角形・四角形に分割
・底辺と斜辺の見方を変えて、面積を計算



斜辺の長さが分かったけど、
「かけて2」じゃ分からないよ・・・



同じ数字をかけると、
4とか9になるはずだけど・・・
中学以降の数学では、この時「①=ルート2 」と習いますが、ここでは「かけて2」が答えです。
・①x①=2
直角二等辺三角形の「斜辺しか分からない」とき
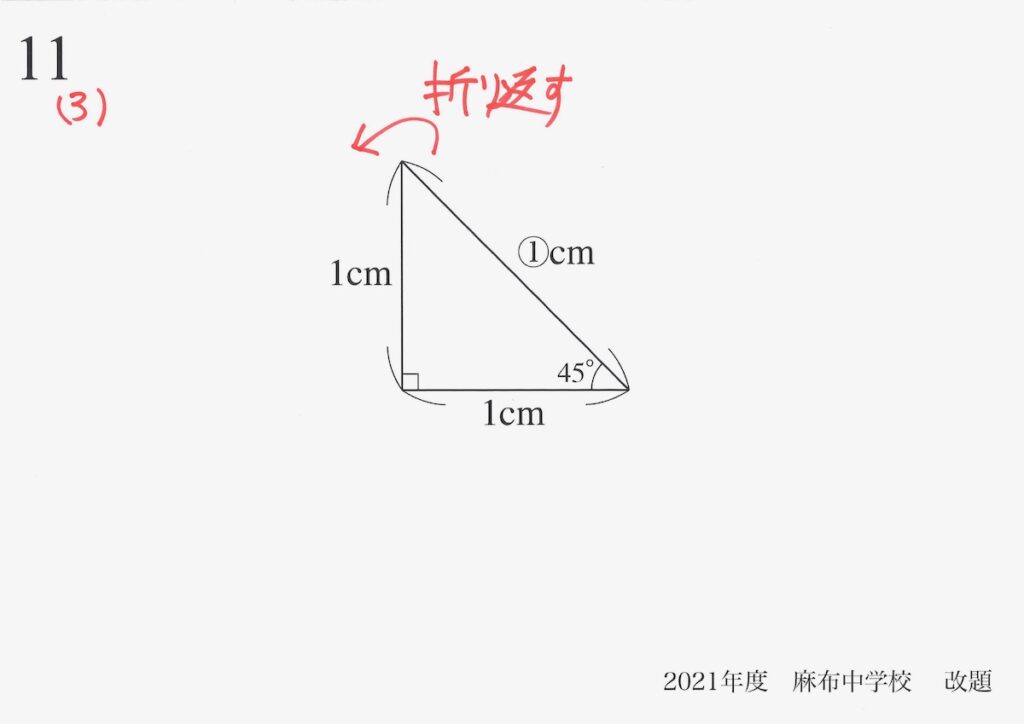

今回の考え方は、「図形の中で相似形を作る」考え方でした。
次は、図形の外に出てみましょう。
「図形の外に出る」考え方は、下記が基本となります。
・線を延長して、平行な直線と組み合わせて相似形を作る
・図形を折り返して、同じ図形をもう一つ作成
直角二等辺三角形を、折り返して考えてみましょう。
この考え方は次回ご紹介します。
直角二等辺三角形の「斜辺しか分からない」時は、



斜辺をかけたら、
元の直角二等辺三角形の面積の4倍!
このような公式を習った方もいるでしょう。
直角二等辺三角形の「斜辺しか分からない」時は、この考え方で大体出来ます。


今回の「図形を分割する」考え方でも、その理由が分かると思います。
次回の「図形を外に展開する」考え方だと、より「斜辺と面積の関係」が分かるでしょう。
次回は下記リンクです。



