前回は「EGWグループ中学志望のお子様へ」の話でした。
立体図形を得意になる勉強法：パップス・ギュルダンの定理
「中学への算数9月号」に興味深い記事がありました。
p50-53の「パップス・ギュルダンの定理」に関する記事です。
流石に小学生が本定理まで知らなくても良いように感じますが、内容としては面白いです。
そして、高校数学にも出てくるような内容を、小学生にも分かるように丁寧に解説しています。
重心の話を、上記リンクでご紹介しました。
算数・理科において、重心は非常に大事です。
この「パップス・ギュルダンの定理」も重心が非常に大事な定理です。
実際に、攻玉社の特別選抜で出た問題ですが、最難関校を志望する方は、目を通しておくと良いでしょう。
男子小学生読んだけど、
難しい・・・
「難しい」と思ったら、
男子小学生ふ〜ん、
そうなんだ・・・
このくらいの気持ちで「ぼんやりと理解」でも良いでしょう。
ペーパーテストと学力
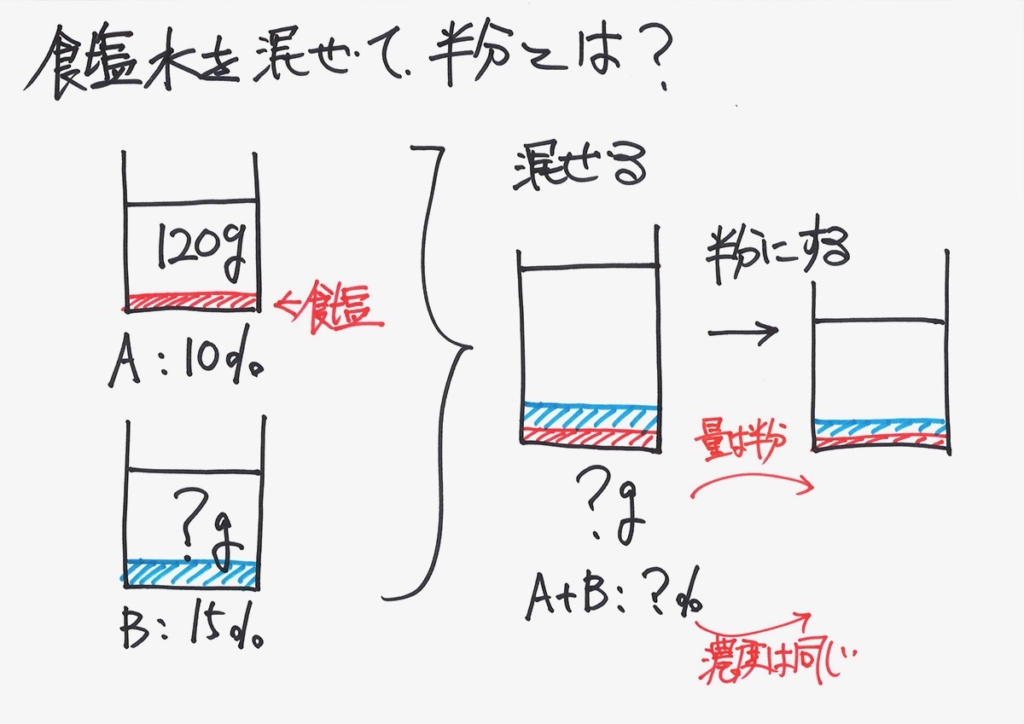
中学受験の入試問題をみると、とても工夫されていることが分かります。
出題者このようなことを
理解しているかをみたい・・・
出題者この問題はこのように表現して、
こうすれば面白くなるかな・・・
各学校の教員の方々は、入試問題作成にはかなりの時間とエネルギーを投入しているでしょう。
いくら試験を工夫しても、
受験生の父親でも、「ペーパーテストはペーパーテスト」
だよね・・・
このような意見もあります。
そこで、「ペーパーテストで出来るだけ学力を適正に図る」ことを、様々な学校が工夫しています。
「パップス・ギュルダンの定理」のように、「中学・高校生対象の定理を小学生向けに出題」は、
受験生の父親中高生が学ぶことを
小学生に問うのは、行き過ぎでは？
様々な方の意見があるでしょう。
筆者は「行き過ぎは良くない」と思いますが、
内野吉貴「小学生の算数への興味を喚起する」意味においては、
良いと思います。
こういう問題は、中高の数学科の先生は考えるのが好きそうです。
「数学好き」だからこそ、このような「定理を様々な角度から考える」のは楽しいのです。
社会でも「考えさせる問題」が、これから増えるでしょう。
日本の「比較的闇の歴史」を明快に出題した麻布中の問題を、上記リンクでご紹介しています。
「公式で解くのではなく、考える力を問う」姿勢
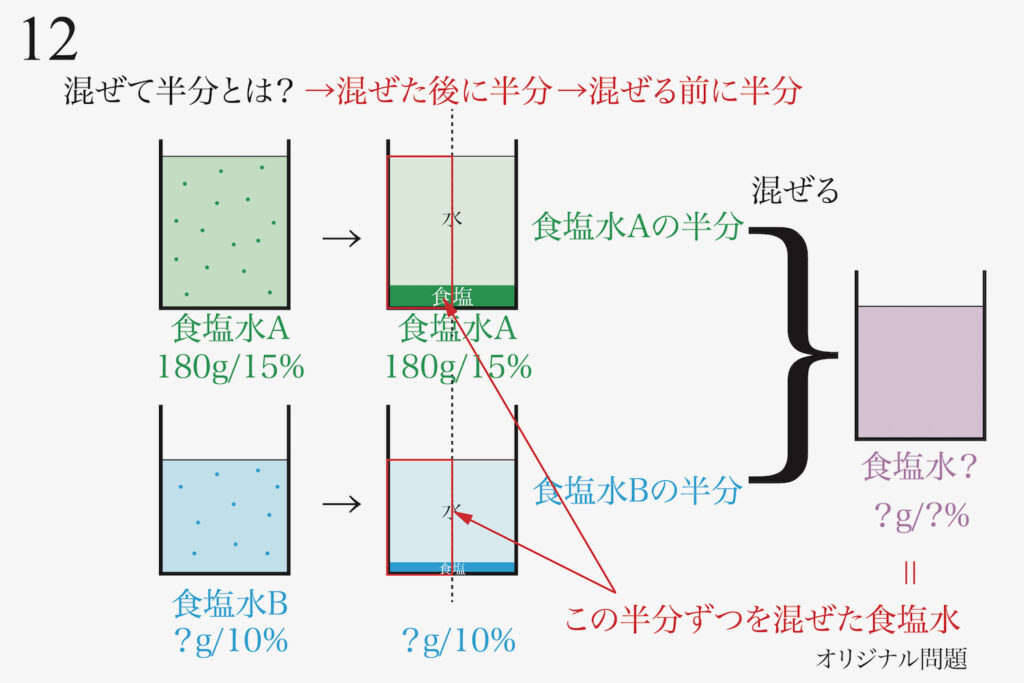
算数・理科において、「公式で解くのではなく、考える力を問う」姿勢が強まるでしょう。
本番でこういう問題が出ても、「落ち着いて取り組めるように準備しておく」のは大事です。
「完全に理解すること」を求めるのではなく、「なんとなく理解」で良いでしょう。
目で追うだけでなく、手を使って描きながら、この記事を読んでみましょう。
こういう「定理などを基にした」問題で、実際に「描いて考えてもらう」タイプの問題も予想されます。
この記事を参考にして「しっかり取り組む」ことは、非常に大きな効果があるでしょう。
男子小学生「パップス・ギュルダンの定理」って
名前が難しそう・・・
男子小学生よく読んでみたけど、
ちょっと分からない・・・
男子小学生やっぱり
難しいけど・・・
「しっかり理解」が大事ですが、「範囲外・難しいこと」は「大体の理解で良い」姿勢も大事です。
次回は上記リンクです。
