動く点と出来る図形の面積のポイント〜大体の傾向をつかむ・グラフを理解・グラフを描いてみる・問題10(5)〜｜面積とグラフ1・算数・過去問・中学受験

前回は「「変化する長さ」を図形的に考えるコツ〜対称性と図形・最小の面積・二次元の面積と一次元の長さ・想像することを楽しむ姿勢・問題10(4)解法B〜」の話でした。

問題10(5)

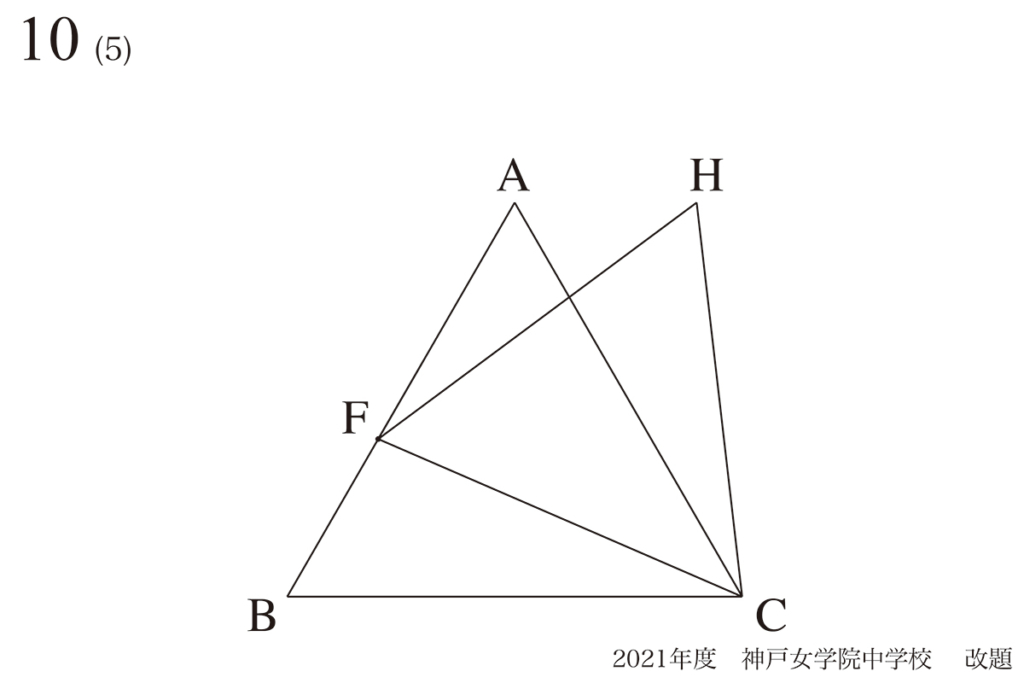
動く点と出来る図形の面積のポイント：大体の傾向をつかむ

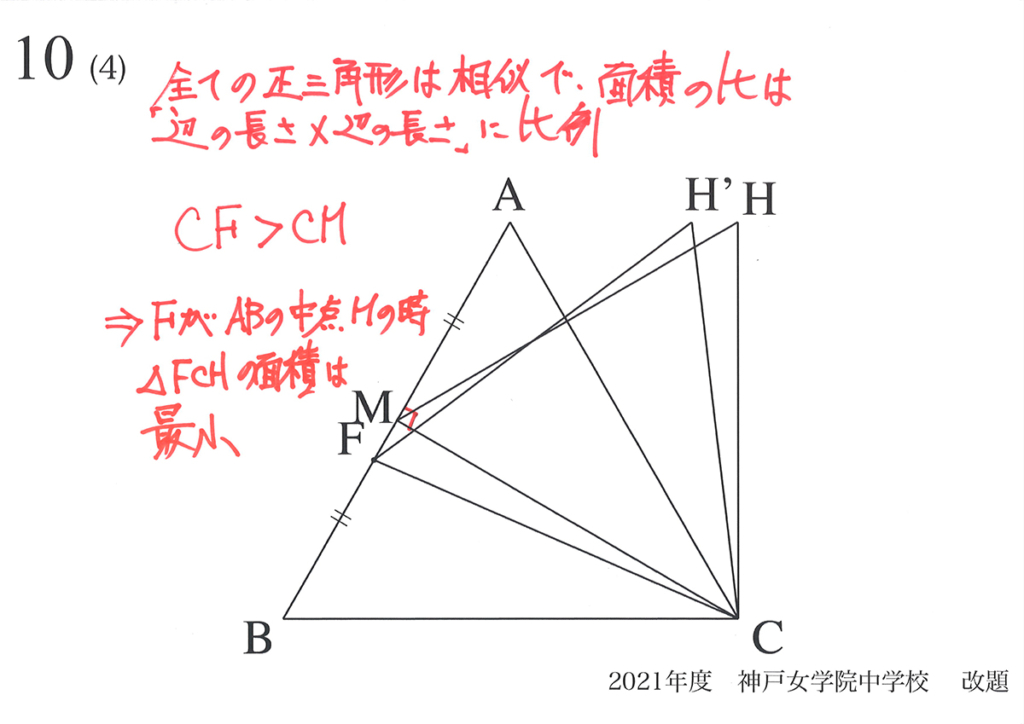
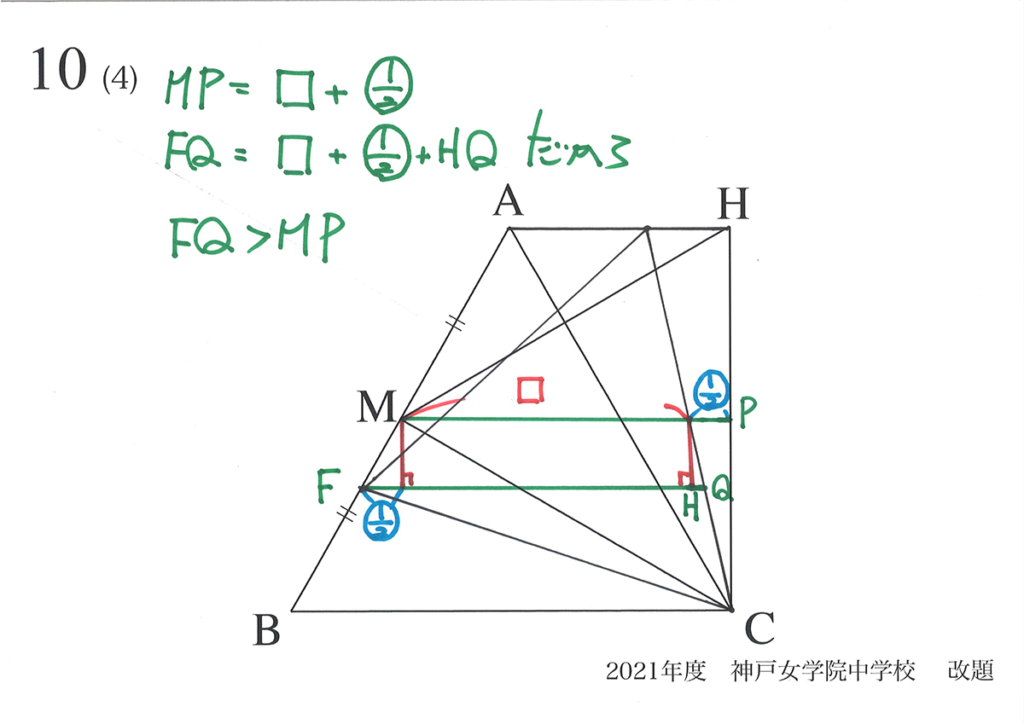
二つの方法で、正三角形HFCが最小となるのは「Fが辺ABの中点Mにある時」と分かりました。

今回は(5)を考えます。

(1)〜(4)までは原題に従い「正三角形の面積=125」としました。

(5)は「正三角形の面積=100」と変更しました。

全体の面積を変えることは、問題の連続性が損なわれますが「面積の割合」が大事と考えました。

急に変わってしまいますが、(5)は「正三角形の面積=100」と頭を切り替えましょう。

この問題は、小学生の範囲を超えています。

「面積の変化する数式を導いてください」や「面積のグラフを描いてください」は中学生の問題です。

そのため、ここでは「グラフのおよその形（概形）を描いてください」としました。

「大体の形」で良いのです。

曲線のグラフは、理科でよくあります。

その意味においては「最難関校で出題の可能性はある」と考えます。

ちょっと分からない方は、下記でご紹介する話をご理解いただければ良いでしょう。

グラフを理解：グラフを描いてみる

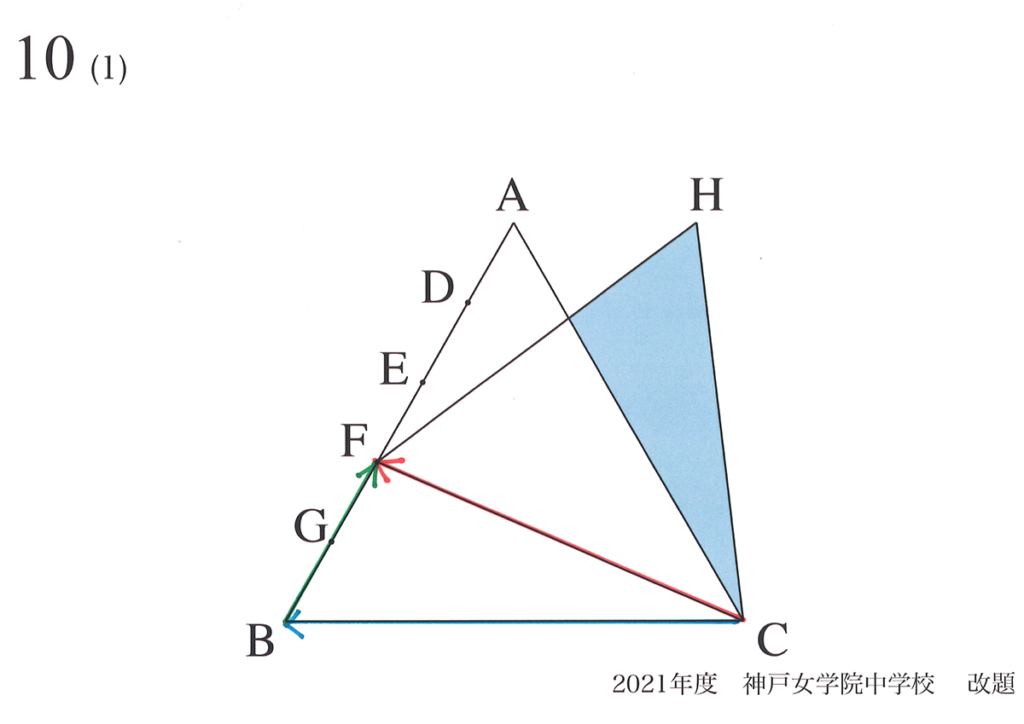
この問題のポイントは、グラフの概形を描くだけではないことです。

「なぜその形になったのか」の理由を書くことです。

算数・理科において、「理由」は非常に大事なことです。

グラフを描く機会は、小学校では少ないと思います。

グラフは中学生以降、物理や化学の授業で描くことが多くなります。

小学校では、棒グラフ、折れ線グラフなどを習って、描いたことがあると思います。

理科の実験問題でグラフが出てきたら、「グラフを理解」する大事さの話をしました。

「グラフを理解」するには、「グラフを描いてみる」ことが最も近道です。

図形問題を「図形を描かないで、頭の中で解く」のは非常に難しいです。

「描かないと分からない、理解できない」図形問題。

図形に限らず、ニュートン算、整数問題なども「書かないと分からない」ことが多いです。

そこで、方眼紙などを利用して「グラフを描いてみる」をやってみましょう。

理科の実験問題などで「グラフを描きなさい」と書いてなくても、問題のグラフを描くと気づくことがあります。

「描くと気づくこと」は、とても大事なことで、学力アップにつながるでしょう。

これまで「寄り道」と(4)で、三角形FCHの面積の何箇所かでの面積（割合）を考えました。

それを参考に、

あまり難しく考えず、気軽に考えてみましょう。

次回は下記リンクです。