前回は「図形の対称性と動く点のコツ〜面積は「長さ・辺の比」・二次元と一次元・対称性から分かること・動く点と動画・予想を検証・問題10(4)解法B〜」の話でした。
問題10(4)再掲載
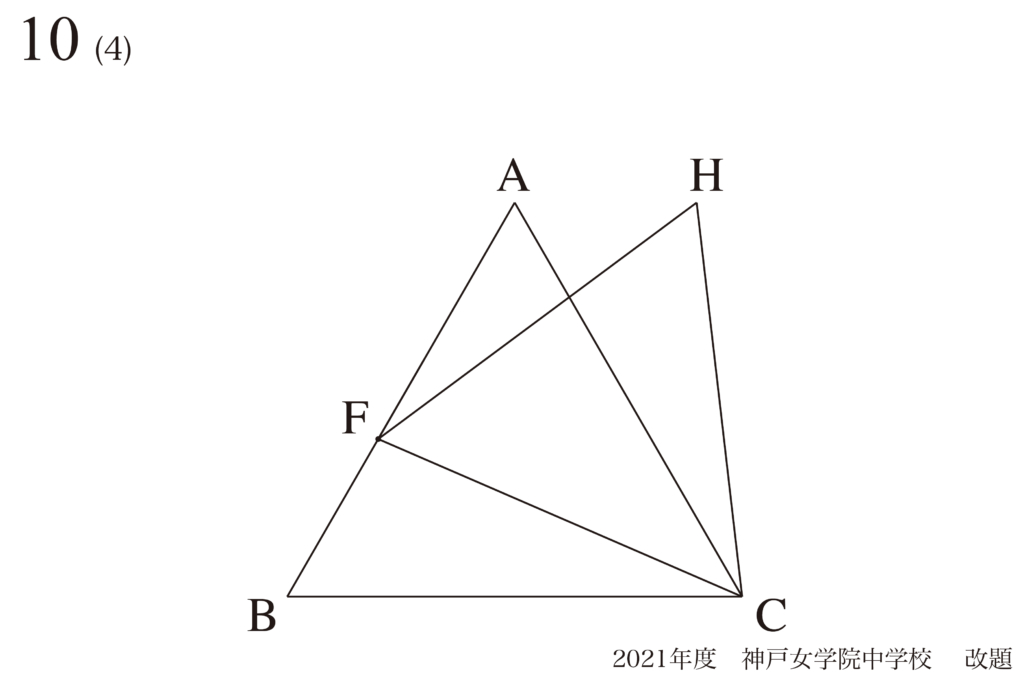
「変化する長さ」を図形的に考えるコツ：対称性と図形
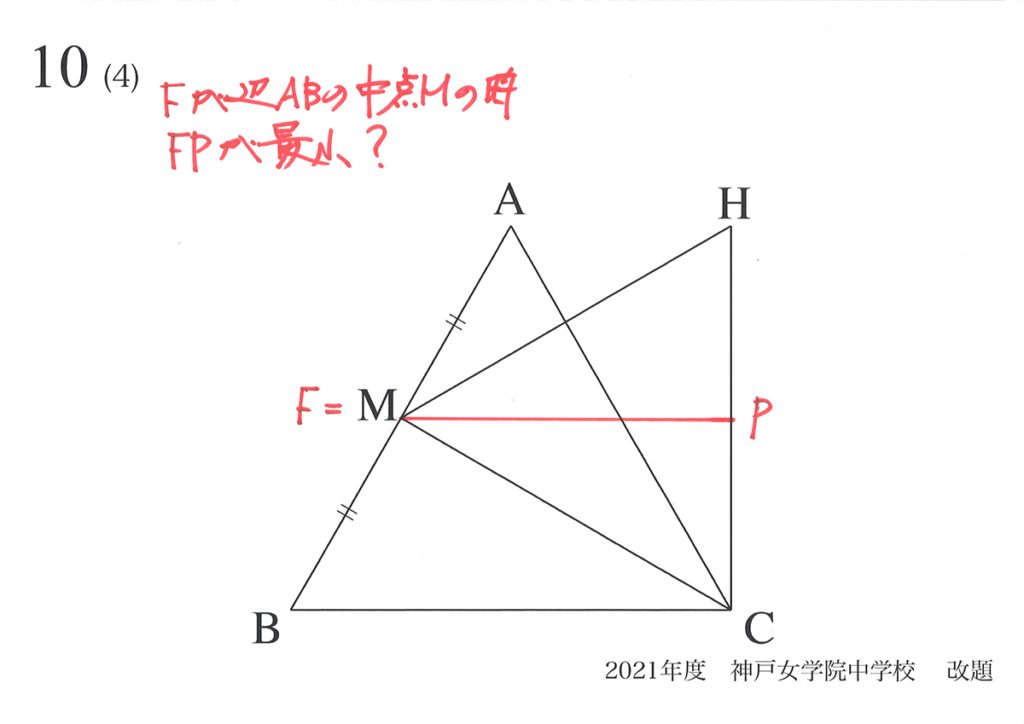
正三角形の対称性から、「BCと平行な直線FPの長さが最小になるのは、点FがABの中点Mの時」と予想できました。
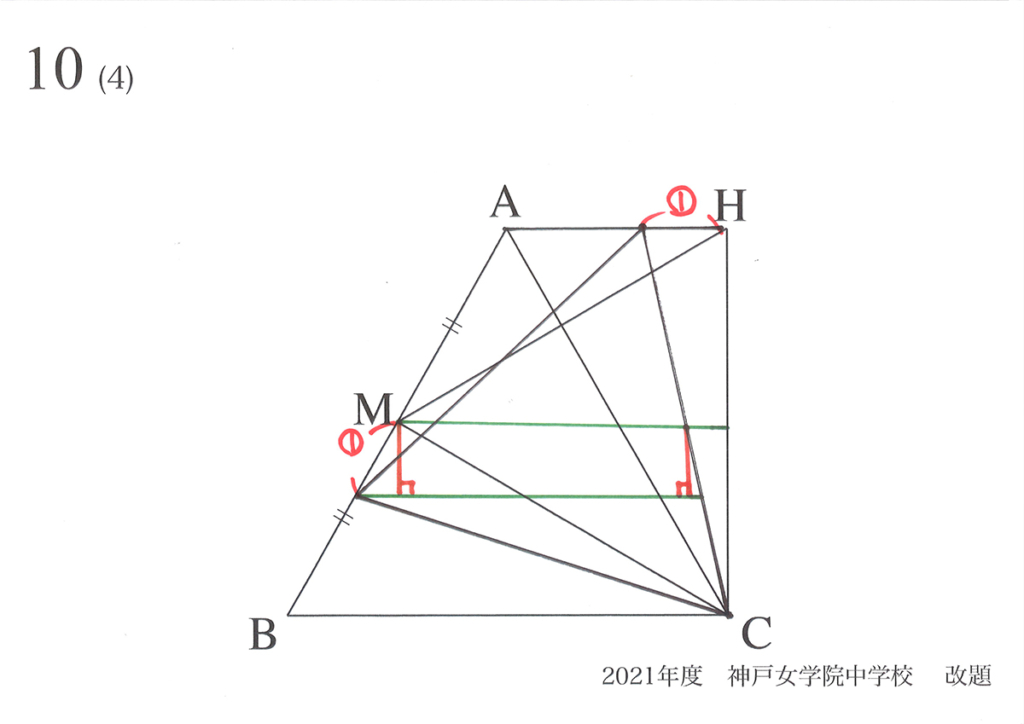
今回は、「FPの最小となる位置は、FがABの中点Mの時」を図形的に求めましょう。
前回、「点FとABの中点Mの距離」=①と置きましょう。
少しずつ、図形的に考えてみましょう。
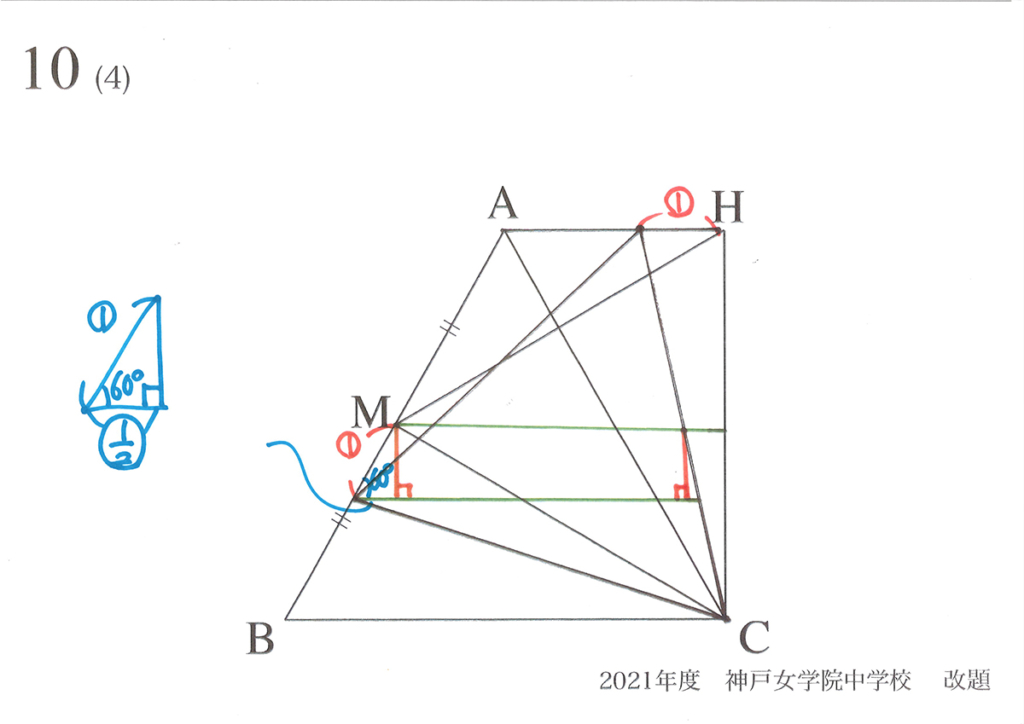
まず、正三角形の性質から、下図の部分の長さ（水色）が分かります。
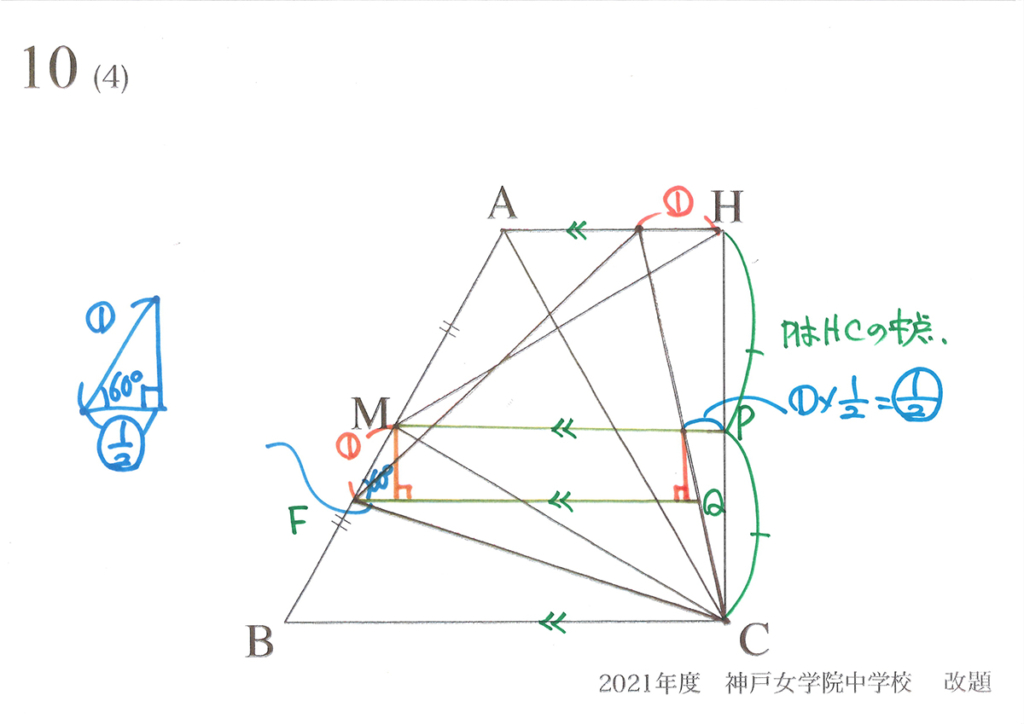
今度は、相似形を考えましょう。
上の図で、点PがHCの中点なので、長さが求まります。
少しずつ「目的となるMPとFQの長さの比較」を考えてみましょう。
・「問題を解くには、Aが分かれば良い」という「Aを考える」姿勢
・「Aを知るためには、どのようなことが分かればよいか」を考える
・少しずつ、着実に答えに近づいてゆく姿勢
男子小学生ちょっと
難しい・・・
難しく考えすぎないで、分かることを考えてゆきましょう。
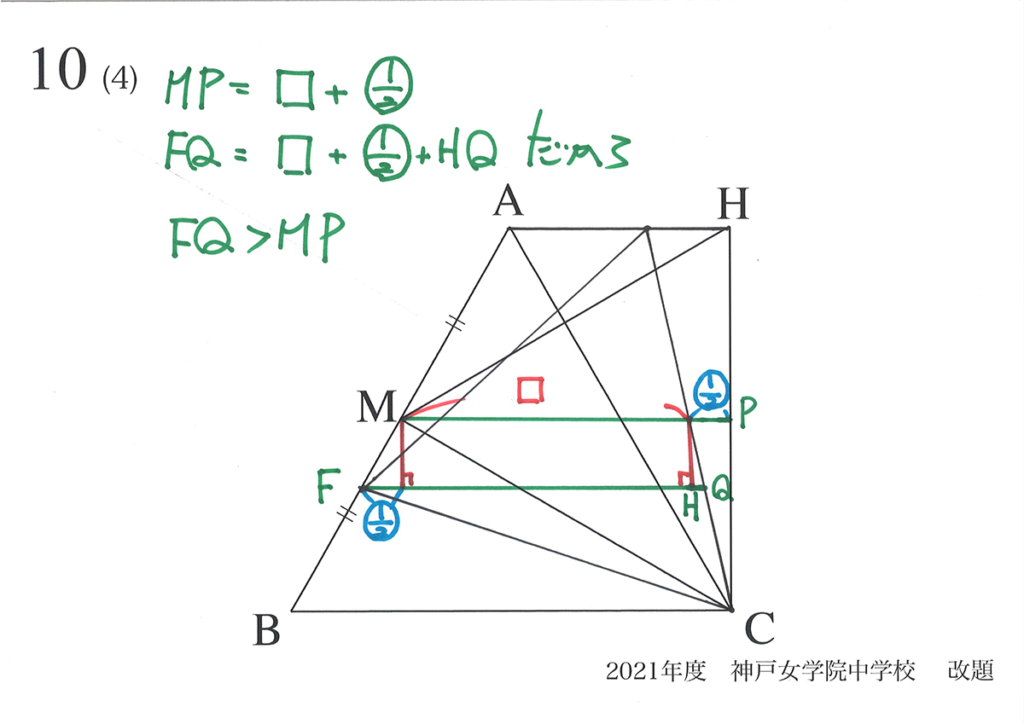
垂線を下ろしたのがポイントで、上の図のように分かります。
垂線から「同じ長さ」が分かり、それぞれ比較すると、「FQ > MP」が分かります。
男子小学生やっと
分かったね！
数学ならば、「長さをa,bなど設置」して方程式で比較的簡単に説明できます。
このような「算数的思考」も大事な学力なので、出来ると良いでしょう。
女子小学生難しいけど、
少しずつ分解するように考えると出来るね！
算数なので、①や□で長さを表現しています。
これらの長さは、自分の好きなように設置してみましょう。
最小の面積：二次元の面積と一次元の長さ
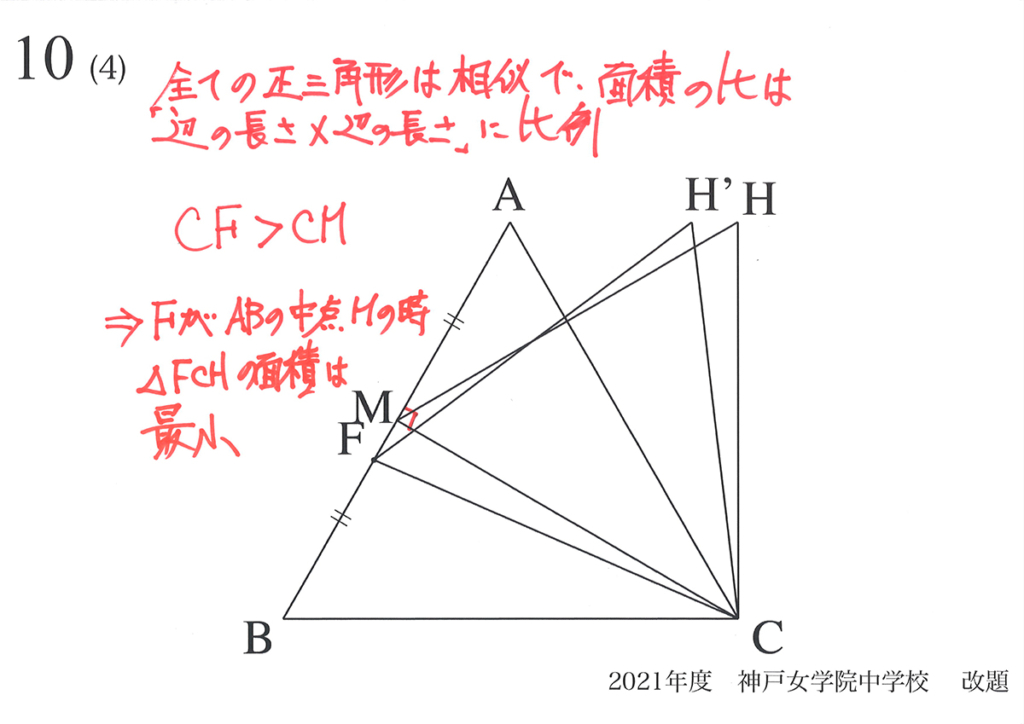
解法Aでは、正三角形の相似比を考えました。
この時は、正三角形FCHの最小値は求めませんでした。
「三平方の定理」を使えば分かりますが、小学校の範囲外です。
面積の基本から、考えてみましょう。
「高さが同じ」なので、面積は「FPの長さに応じて大きくなったり、小さくなったりする」です。
つまり「正三角形の面積は、FPの長さの変化と同じように変化」します。
・長さは「cm」「m」など一次元
・面積は「cm2「「m2」 など、「単位に小さな2がつく」二次元
「面積の比較」が「長さの比較」になるので、簡単になります。
・比較する対象の次元を小さくできないか、考える
・面積は「長さx長さ」で二次元、長さは一次元なので、一次元の方が簡単
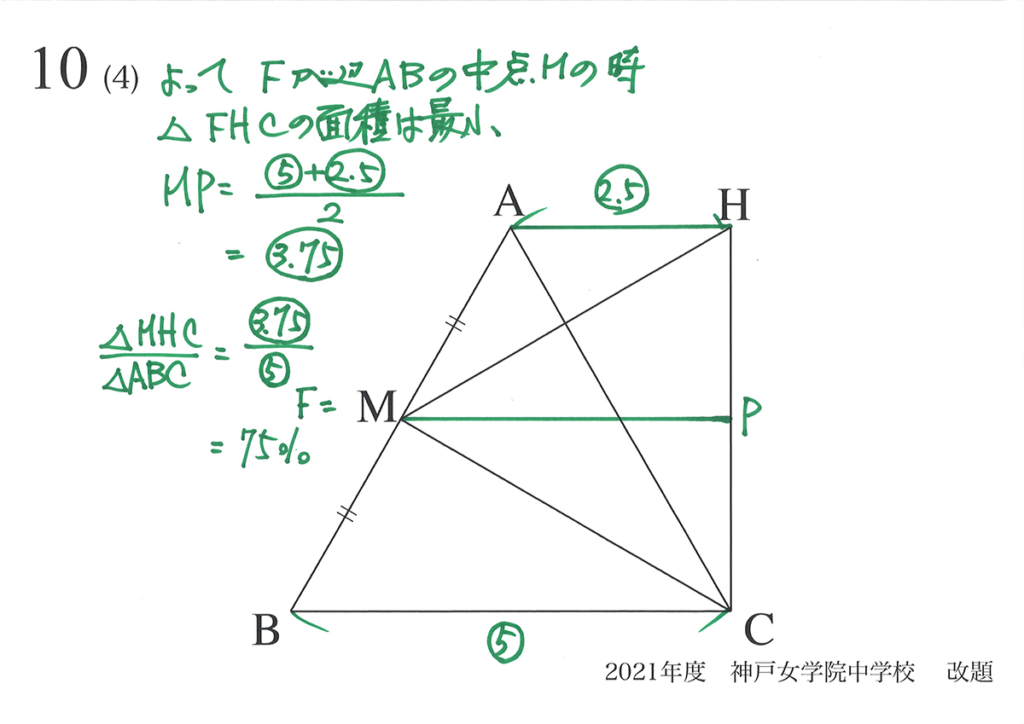
FがABの中点Mの時は、FP=MPの長さは、平均を取れば分かります。
これで、正三角形FCHの面積の最小値は、「正三角形ABCの75%」と分かりました。
想像することを楽しむ姿勢
男子小学生答え聞いたら分かったけど、
自分でやるのは難しいよ・・・
今回の解き方は、少し難しいです。
そのため、「解答を理解できたらOK」くらいな気持ちで十分です。
女子小学生解答を読んでわかれば
いいの？
解答例を読みながら、ぜひ手を動かして、図形を考えてみてください。
・問題を解く途中で諦めずに、しっかり進めてゆく大事な力
・「こう考えれば解けるはず」という、目標を明確に持つ大事さ
・根気や努力は「将来何かを成し遂げる」ために最も大事な力の一つ
「根気よさ」もまた大事な学力です。
小問などで「誘導付き」なら、こういう問題の出題がありえるでしょう。
対称性（折り返したら同じ）から、予想しましたが、このように
男子小学生ひょっとして、
こうかな？
このように「想像すること」を楽しみましょう。
想像したことが「違うこと」もあります。
男子小学生あれ？
違う・・・
間違えたり、違うことがあるのは当たり前のことですから、どんどん考えましょう。
そういう気持ちを持つことが、算数の学力アップにつながります。
次回は下記リンクです。
