前回は「動く点と出来る図形の面積のポイント〜大体の傾向をつかむ・グラフを理解・グラフを描いてみる・問題10(5)〜」の話でした。
問題10(5)（再掲載）
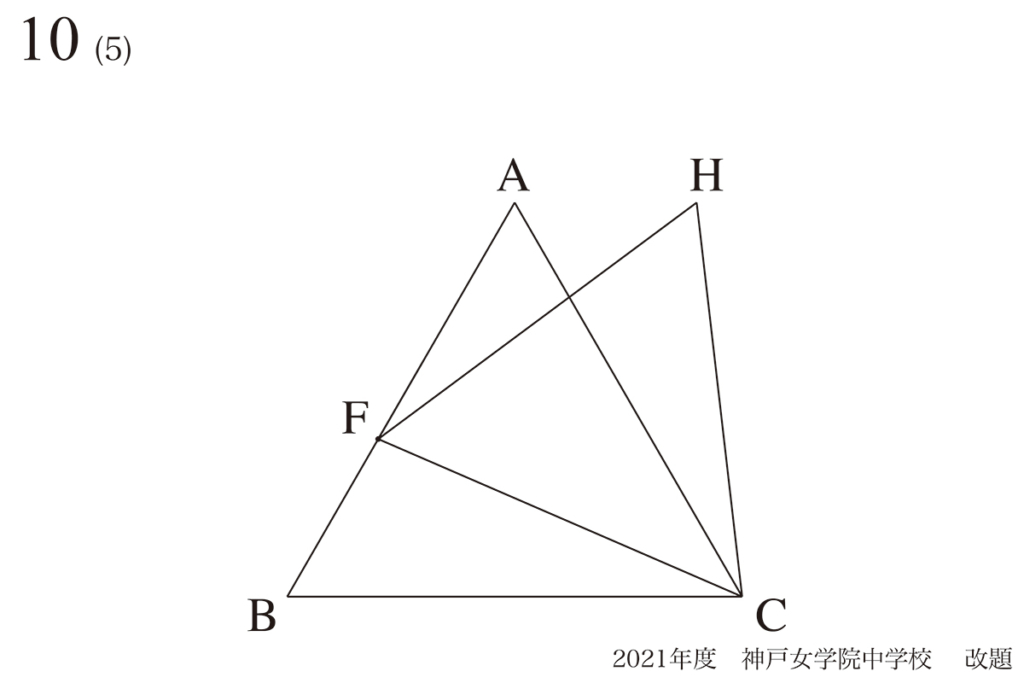
動く点と図形の面積のグラフを描くコツ・ポイント
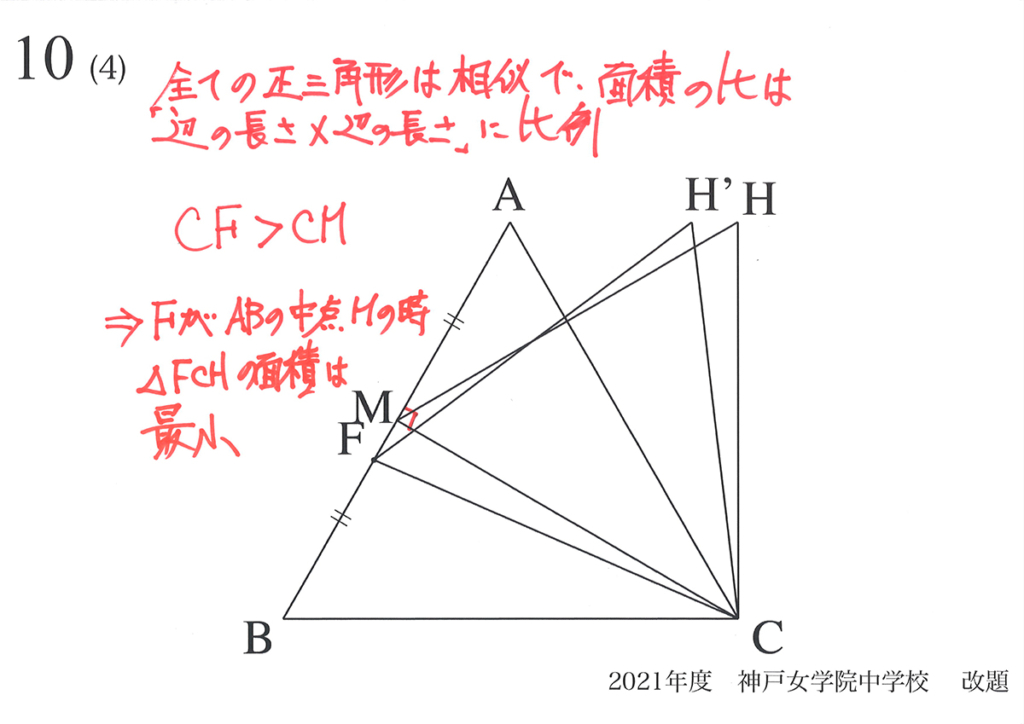
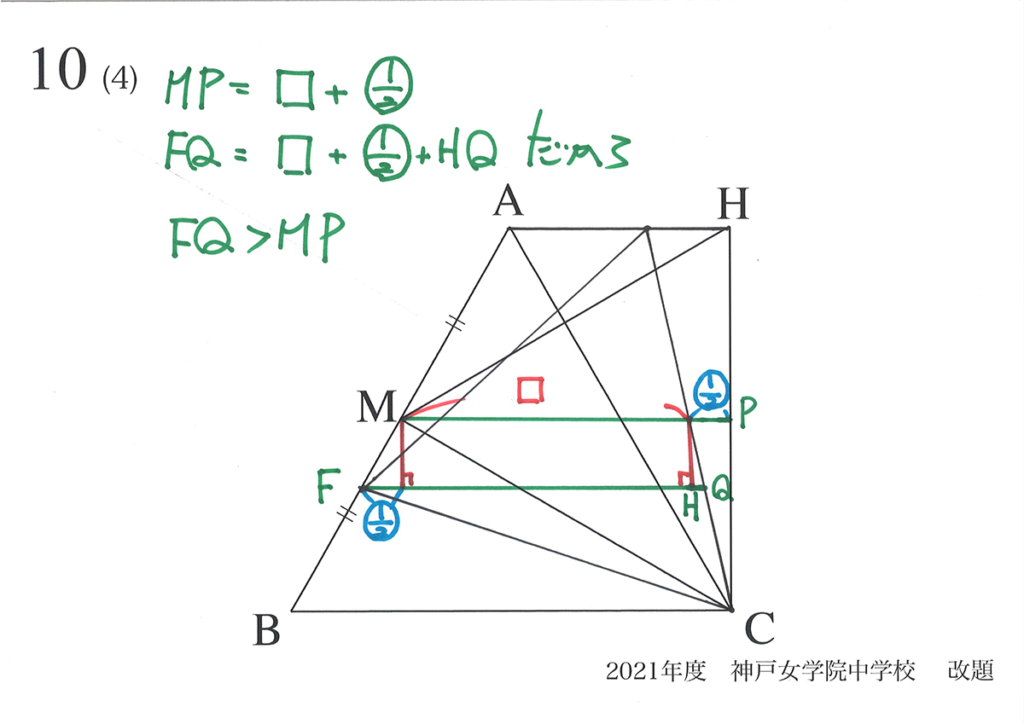
点Fが辺BA上をBからAに移動するとき、正三角形HFCの面積は「Fが辺ABの中点」の時、最小となります。
そして、「正三角形HFCの面積がどのように変化するかのグラフ」を具体的に考えてみましょう。
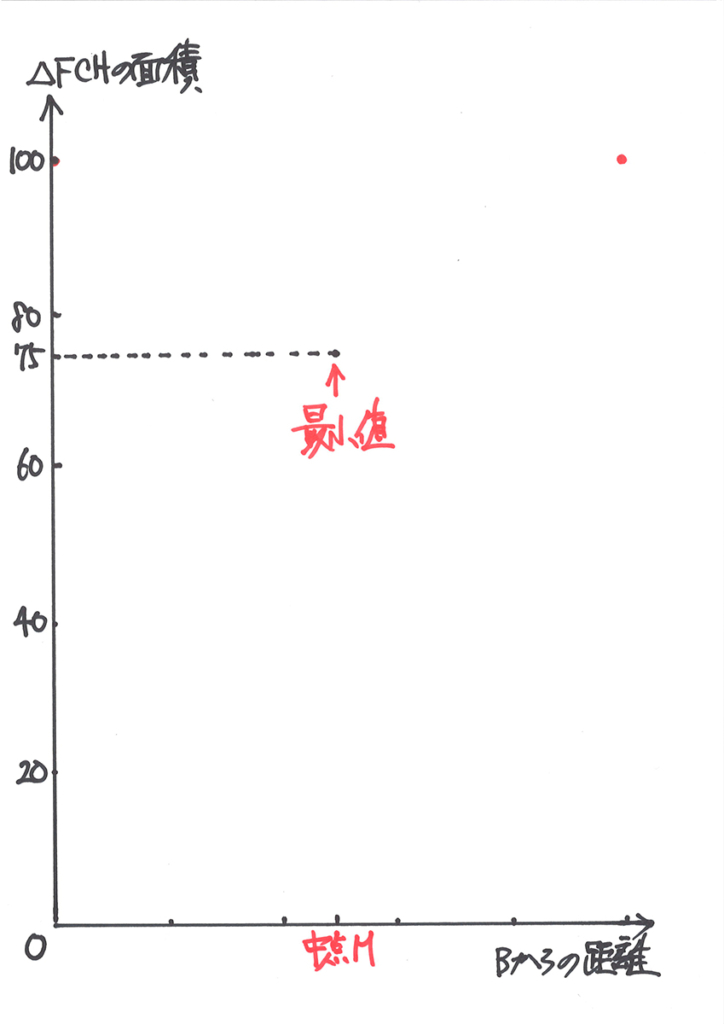
グラフを描くときは、部分的に描かず、全体を描くようにしましょう。
ここでは、BからAに向けて点F（動点P）が動いてゆきます。
動く点は「動点P」と表記されることが多いです。
今回のような問題では、縦軸の「最小値から下」は関係ないです。
理科の実験問題では、「縦軸・横軸が0から始まる」ことが多いです。
実験では「0以下（マイナス）が大事なこと」もありますが、それは高校以上なので「0以上」とします。
確かに
実験問題では、温度とか長さとか0〜あるね・・・
でも、関係ないなら
あっても意味ないんじゃないのかな・・・
「関係ない」ですが、上の方だけ考えると全体的なスケール感が分からなくなってしまいます。
この問題のように「変化する割合」を考えるとき、「〜％はどのくらいの量か」を実感することが大事です。
方眼紙などに、縦軸も横軸も、原点0が現れるように描きましょう。
・全体的なスケール感が大事
・原点（0）が表示されるように、大きく描く
ここでは「画面の分かりやすさ・見えやすさ」を重視して、上部のみ表現します。
まずは最大・最小：最も大きな特徴を考える
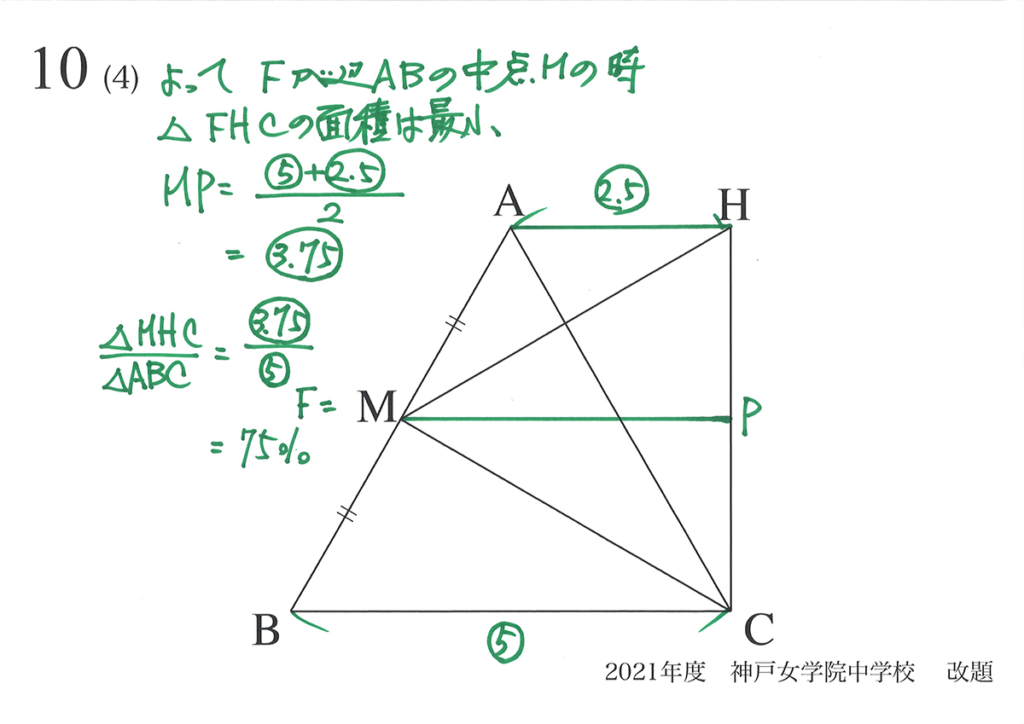
(4)で△FCHの面積の最小値は75と分かりました。
「動点Fが点B」にある時、そして「移動した最後=点A」にある時は、面積は最大の100となります。
動点Fが点Aにある場合は、具体的に考えなかったですが、矢印の話を考えると分かるでしょう。
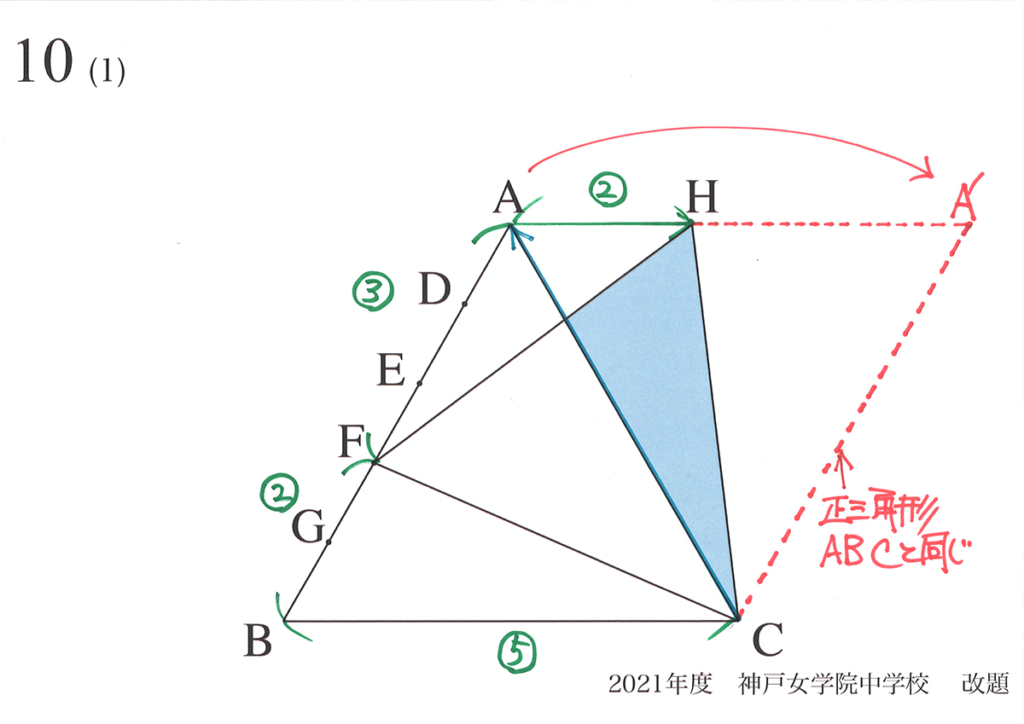
これらを元に、まずは最大・最小を考えます。
まずは
「最大と最小」なの？
グラフを考えるとき、グラフを読むときは「最も特徴的な状況」を把握することが大事です。
確かに
「最大と最小」は大きな特徴だね！
・最も大きな特徴である「最大・最小」を把握
・グラフの直線・曲線の大体の雰囲気と傾向を把握
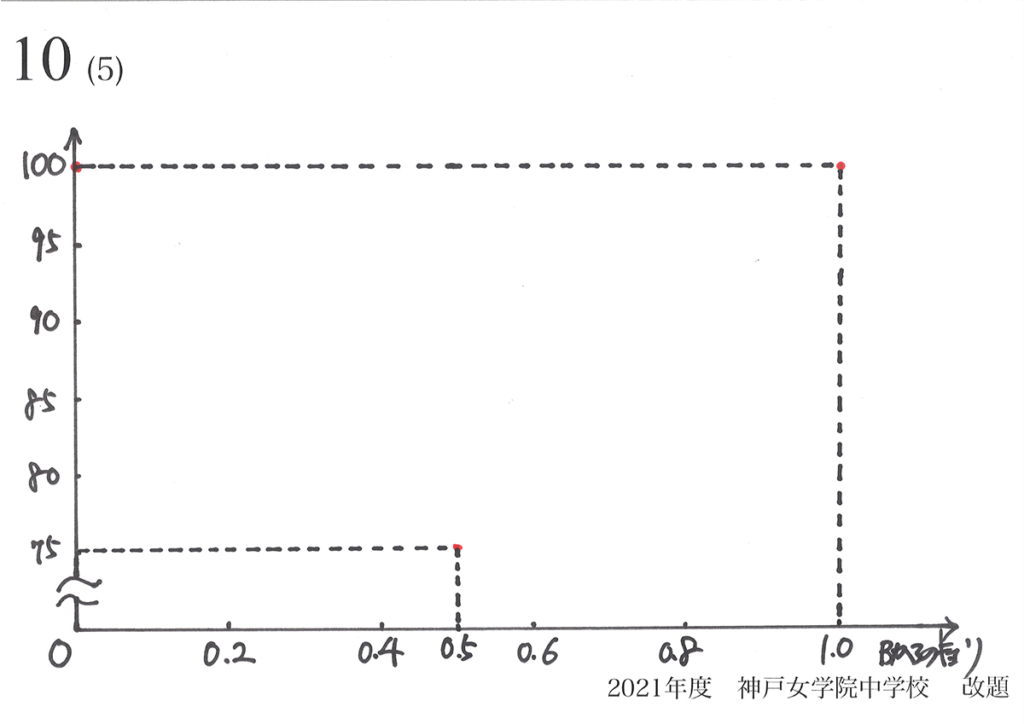
具体的に「最大と最小となる点」をプロットしてみましょう。
横軸は「辺BAの距離=1.0」と考えましょう。
辺BAの中点Mは、1.0/2=0.5の位置となります。
上のグラフで赤い点が「最大と最小となる点」をプロットした点です。
図形の対称性とグラフの対称性
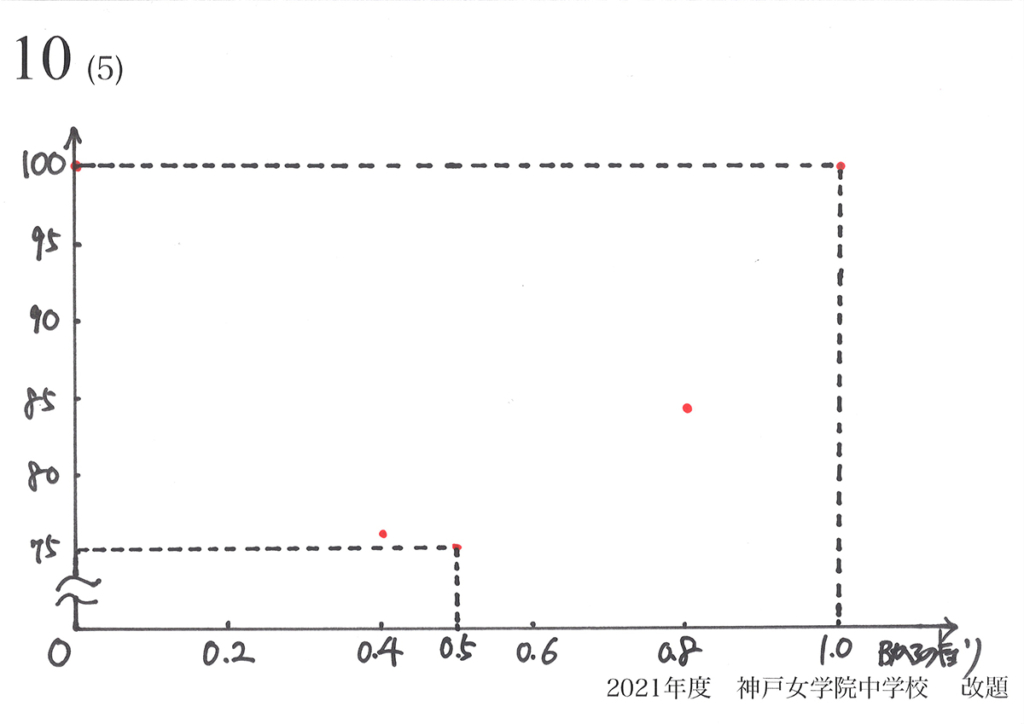
次に「寄り道」で分かった、76と84をプロットしてみましょう。
(1)(2)で問題には出ませんでしたが、寄り道で考えたことが「問題で誘導されている」と考えます。
ここからは、大事な対称性を考えてみましょう。
動点Fが辺BCの中点Mにある時を境に「同じ」になります。
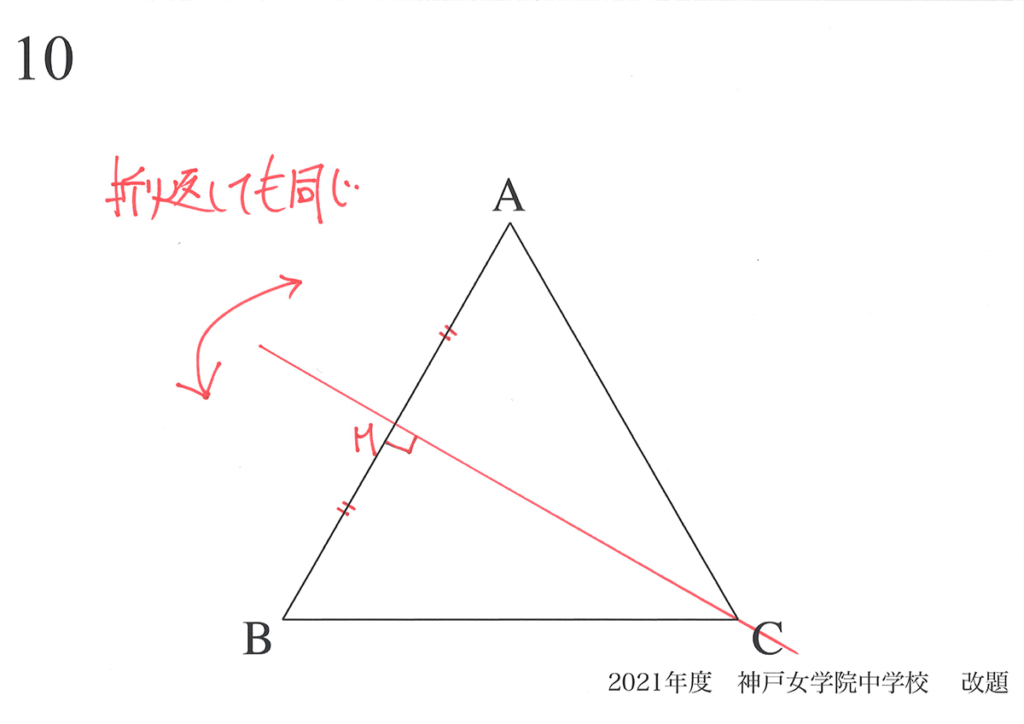
・ある線で折り返すと、きれいに折り返せる（折り返したら同じ）
・対称性のある図形には、様々な特徴（辺の長さが等しい、角度が等しい）がある
そこで、面積のグラフも同様に「対称性をもつ」ことになります。
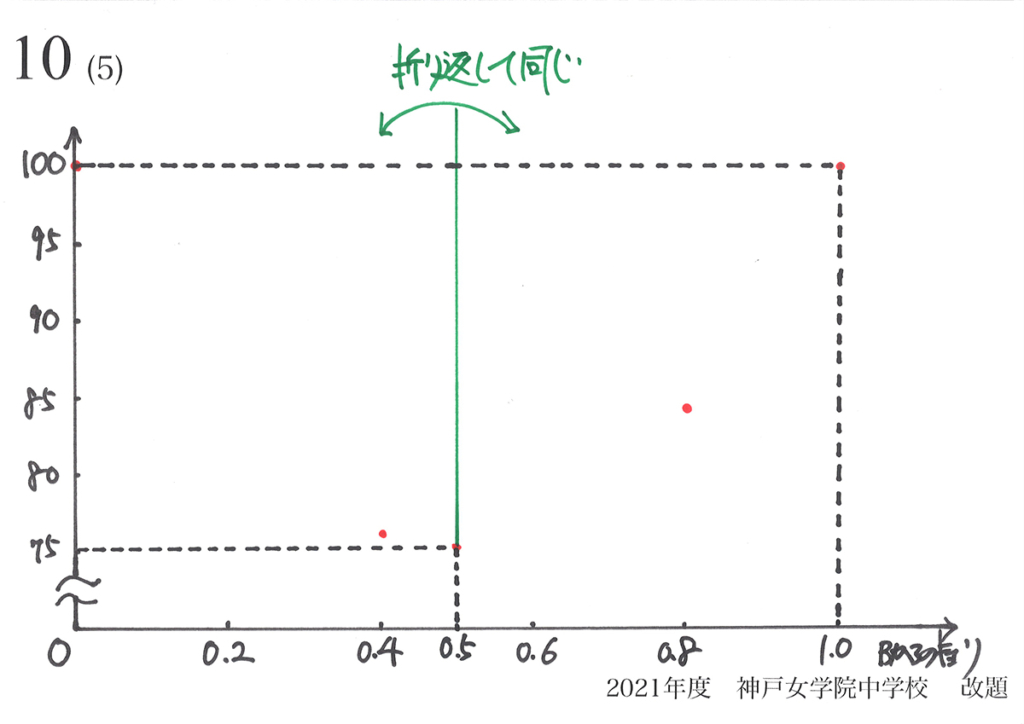
図形が「対称性を持つ」とグラフは、どうなるでしょうか。
図形的に「折り返して同じ」
だから・・・
あっ、
ひょっとして！
この続きの話は、次回ご紹介します。
