前回は「面積比を描いて理解して図形を得意に〜方眼紙のイメージ〜・面積比を計算して理解・四角形の相似形の面積比・大きい対象は小さく分割・問題10(4)ポイント〜」の話でした。
問題10(4)再掲載
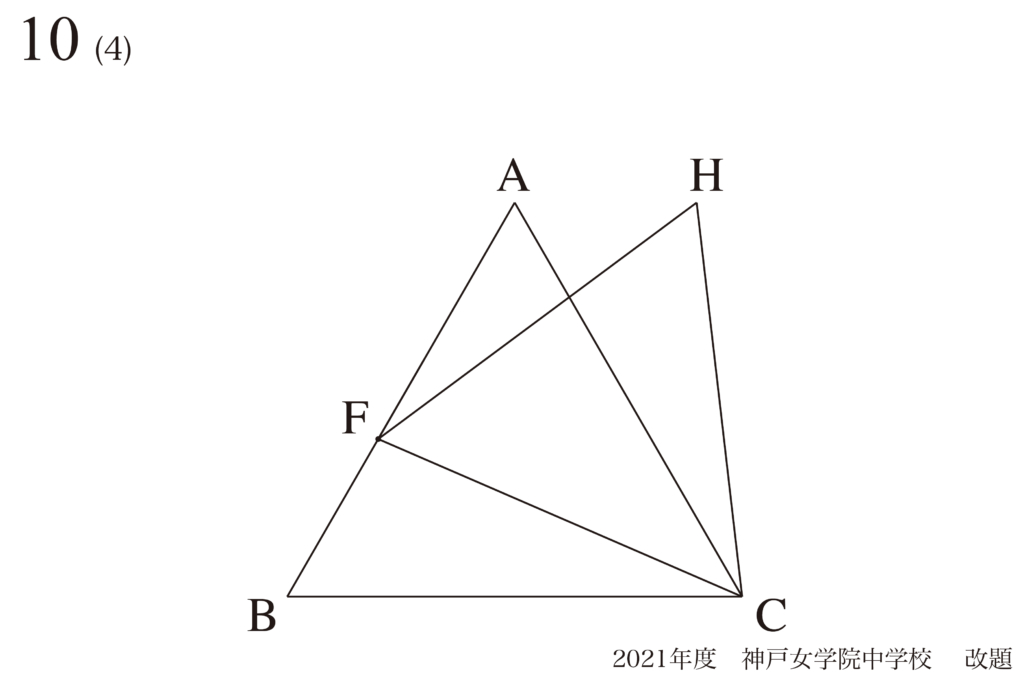
図形問題を得意になる勉強：図形の対称性
今回は「正三角形の大事な性質」を考えましょう。
「正三角形の描き方」の話を、上記リンクでご紹介しています。
正三角形は「全ての辺の長さが等しい」と「全ての角度（内角）が等しい」です。
これは、正方形・正五角形・正六角形・・・・・など正〜角形に共通する基本的性質です。
そして、もう一つ大事な性質があります。
それは「対称性を持つ」です。
「対称性」とは「ある線で折り返すと、きれいに折り返せる」ことです。
男子小学生「対称性」って言葉は、
数学みたいで、難しいよ・・・
言葉が難しく感じるようでしたら、「折り返したら同じ」という考え方で良いです。
こういう言葉が分かるかどうか、というのは、算数の能力とは大して関係ありません。
女子小学生こういう「難しいこと」が分かる人って、
算数のセンスが高いと思っていた・・・
・ある線で折り返すと、きれいに折り返せる（折り返したら同じ）
・対称性のある図形には、様々な特徴（辺の長さが等しい、角度が等しい）がある
難しく考えすぎず、安心して下さい。
正三角形の対称性と特徴
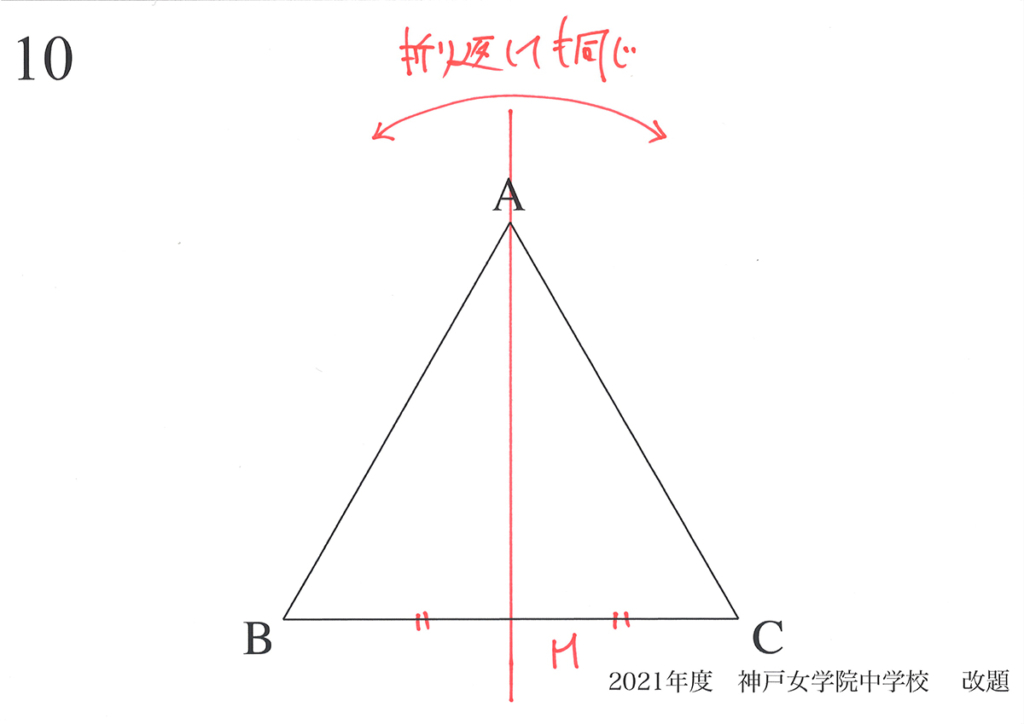
具体的に、正三角形の対称性を考えてみましょう。
まず、下の図のような「折り返したら同じ線」が見えます。
頂点Aを通る「対照となる軸の直線」は辺BCの中点（真ん中の点）Mを通ります。
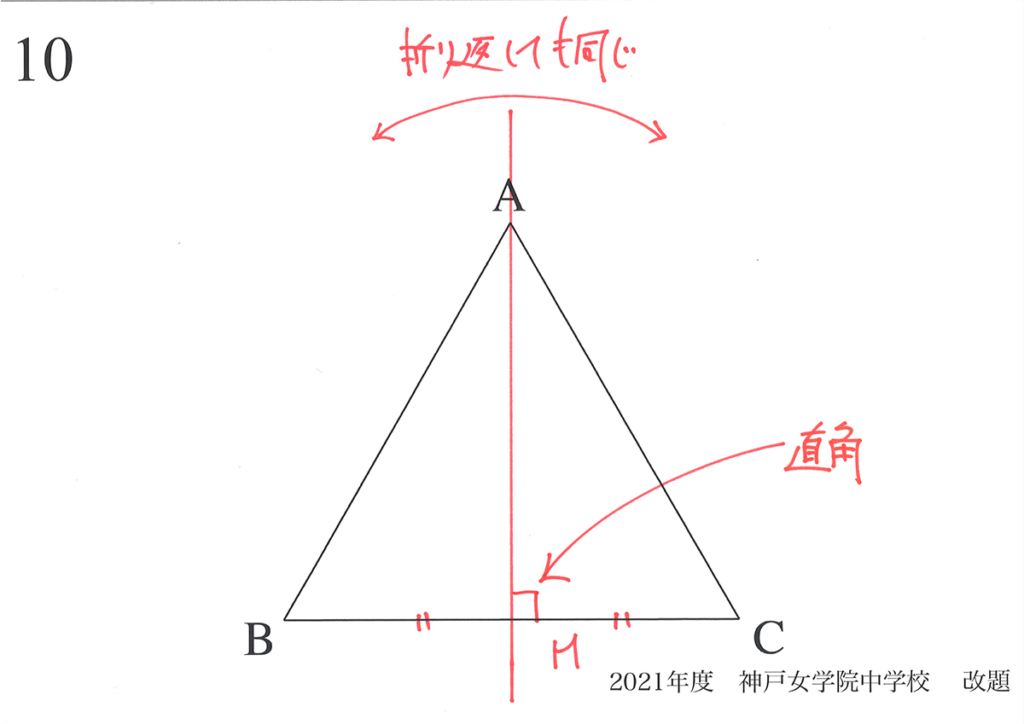
この時、大事な性質があります。
それは「角AMB=角AMC=直角」となることです。
男子小学生あっ、ここにも
対称となるとなる線があるよ！
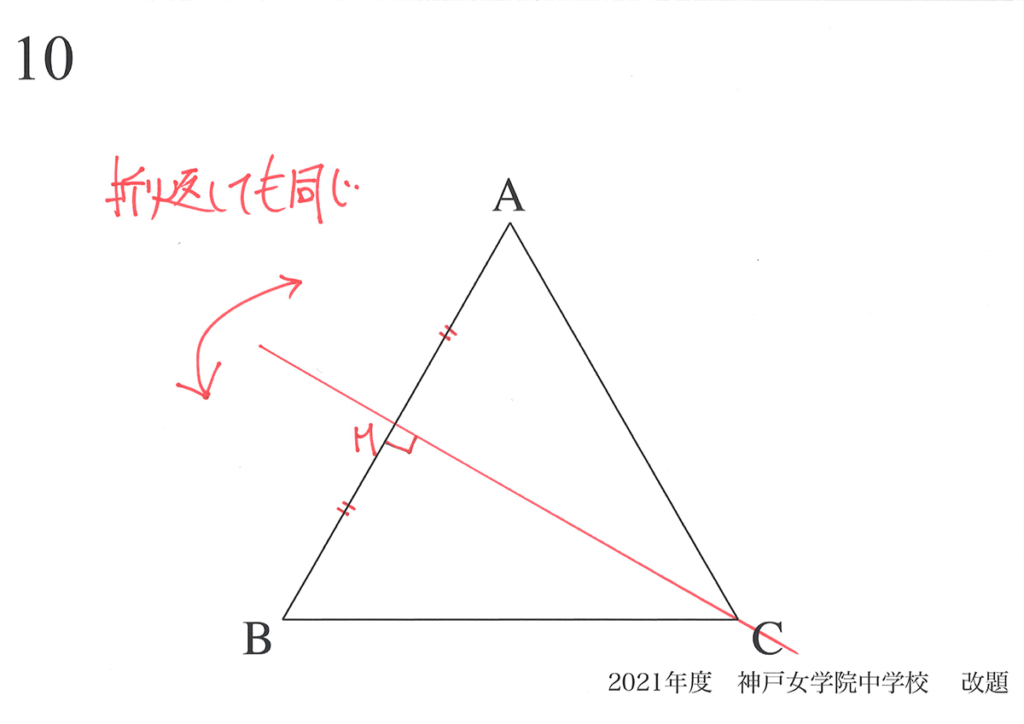
他に「対称となる軸の直線」はあるか、少し考えてみましょう。
女子小学生あっ、ここにも
対称となるとなる線があるね！
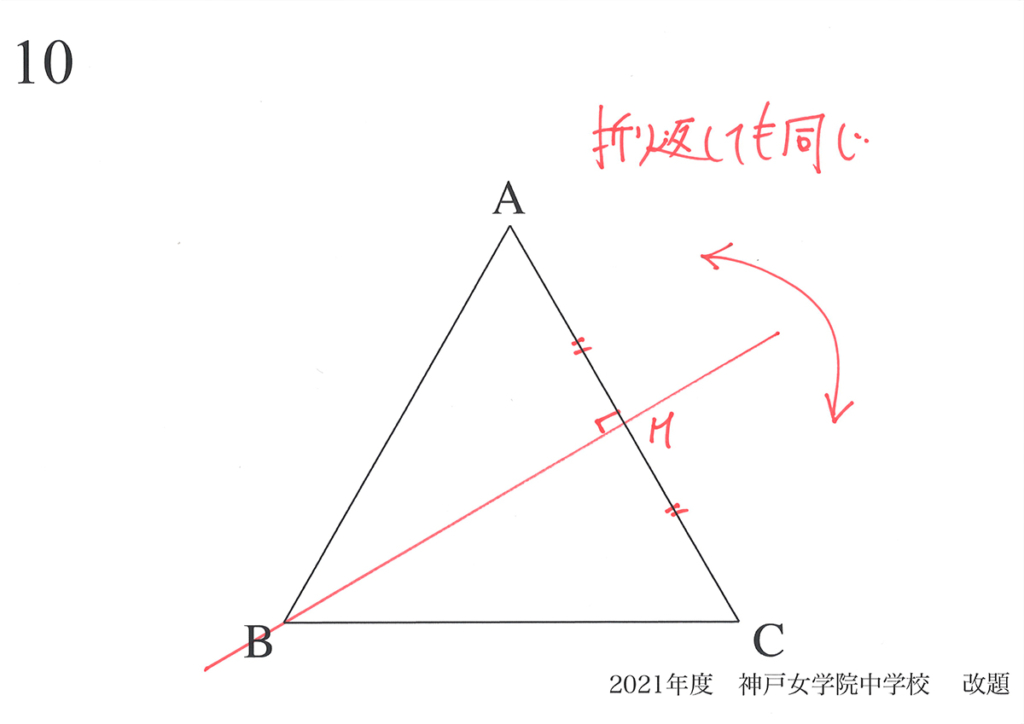
他に2本の「対照となる軸の直線」があります。
正三角形も、これら「対称となる軸の直線」も「正三角形の中心で回転して同じ」になります。
対称性から分かる大事なこと：動点Pの動きと対称性
対称性というのは、算数では非常に大事な性質です。
「対称な図形」が出てきたら、必ず「対称となる軸・中心」を考えましょう。
正六角形の問題を考えるとき、「中心となる点Pと対称軸」を考えたら、解く方向が分かります。
正六角形の問題を解くコツを、上記リンクでご紹介しています。
・対称となる軸・中心・重心を描いて考える
・対称となる軸をいくつか考えてみる
(4)で対称性を具体的に「考えてみましょう。
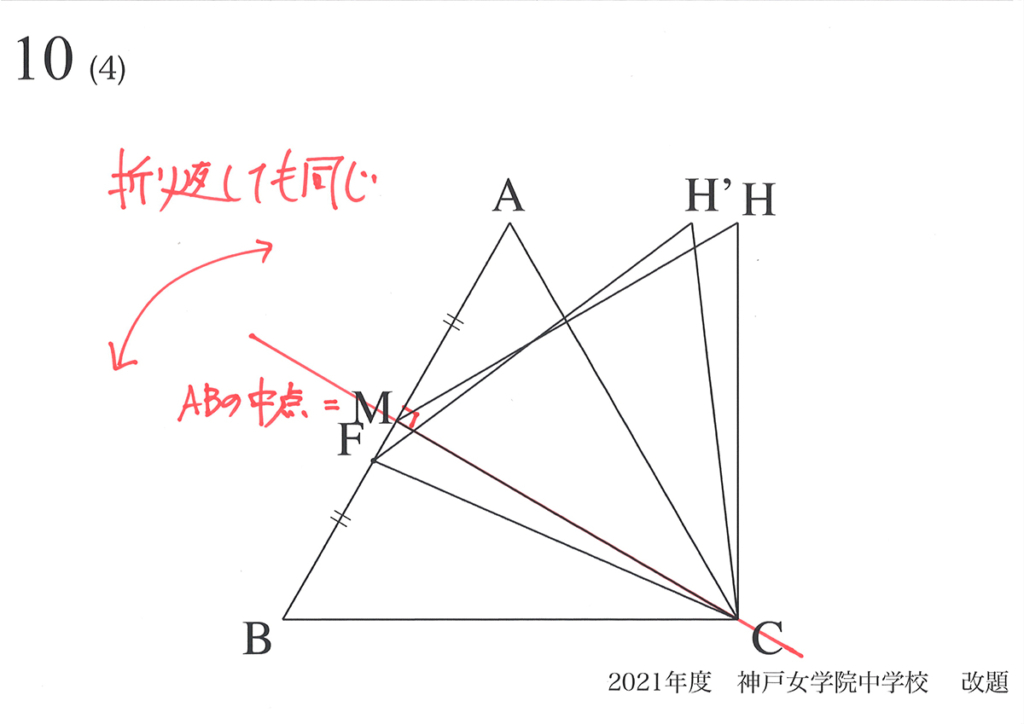
頂点CからABの中点Mを結んだ「直線CM」を考えます。
この直線CMは、三角形ABCの「対称となる軸の直線」です。
女子小学生あれ、ひょっとしたら
対称だから・・・
対称だと「折り返したら同じ」です。
男子小学生「折り返したら同じ」だから、
点Fが頂点Bから頂点Aに移動していくと・・・
男子小学生点Fが、辺AMと辺BMにある時で
同じように考えられる！
これが、この問題の最も大事なポイントです。
これで、かなり答えに近づきましたので、もう少し考えてみましょう。
女子小学生でも、なぜABの中点Mが、
出てくるのかな？
女子小学生これが分からないと、
先に進まないのかな？
この「ABの中点M」を考えるのは「対称となる軸を考えた」結果です。
女子小学生「対称となる軸」から
「ABの中点M」を思いつくんだね・・・
女子小学生なんか
分かった気がする！
「中線AMという補助線」が、この問題の最大のポイントです。
それは「対称性」から考えたことです。
このように図形問題では、「平行」「対称=折り返して同じ」などを考えましょう。
すると、「大事な補助線」が見えてくるでしょう。
次回は下記リンクです。
