前回は「図形問題が「苦手」から「分かる」考え方〜正三角形・辺の比と面積比・類似する解き方・問題10(2)〜」の話でした。
問題 10(再掲載)

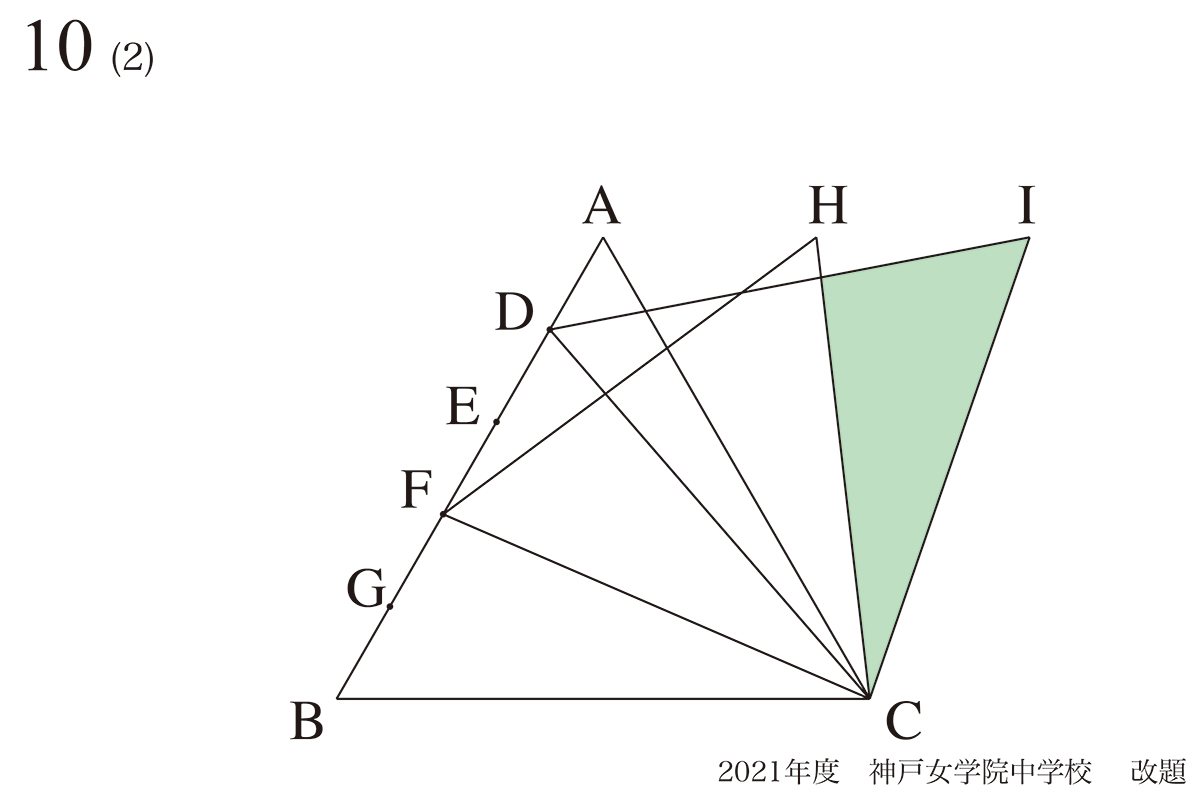
同じ考え方の図形に共通する性質:正三角形HFCと正三角形IDC
(1)と比較すると「新たな正三角形がもう一つ」出てきました。
正三角形HFC・正三角形IDCは「同じ作り方」で出来た正三角形です。
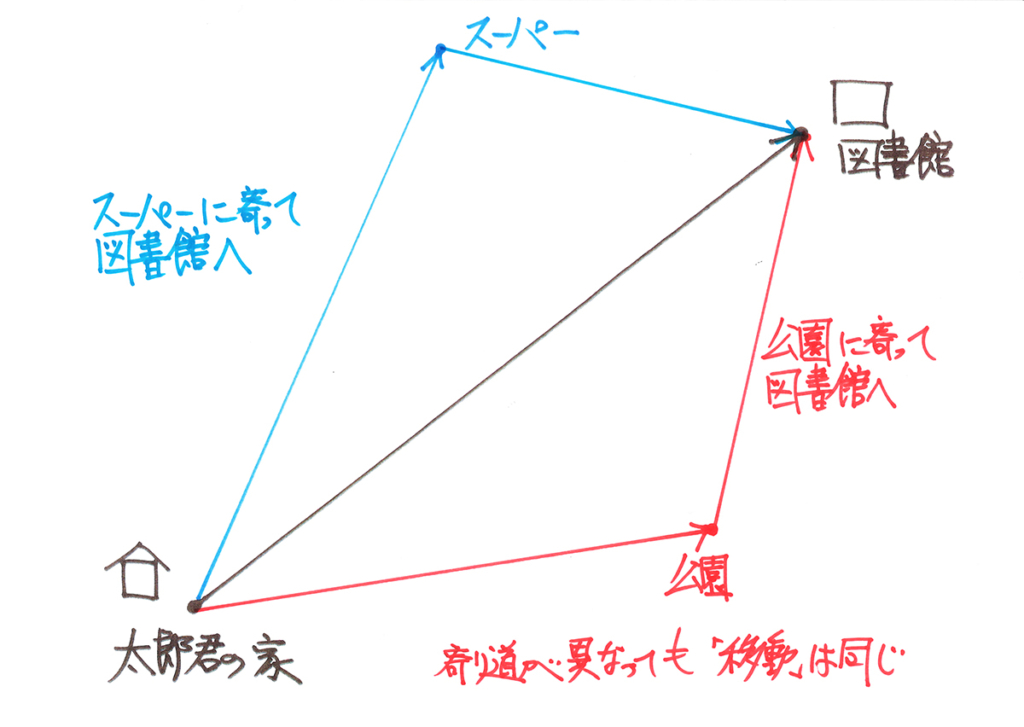
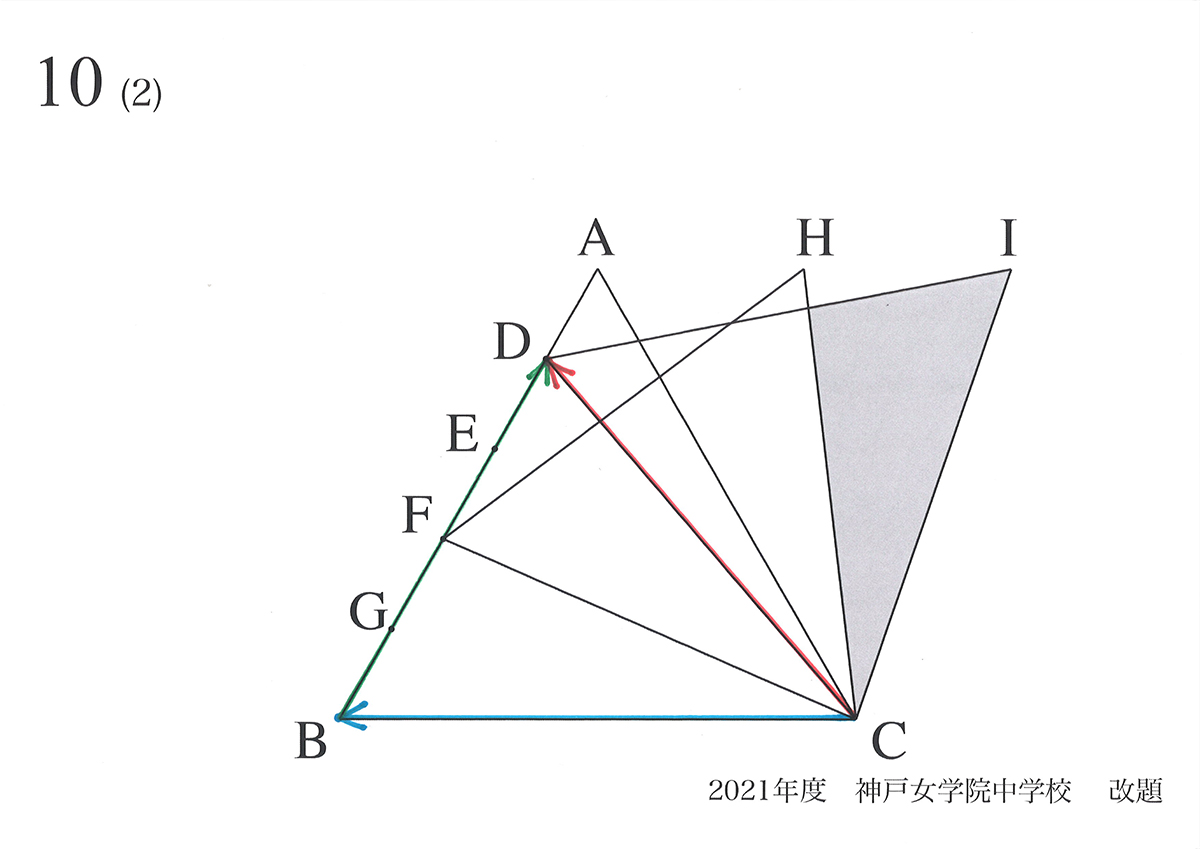
(1)と同様に「矢印の考え方」で図形を考えてみましょう。
図形問題を矢印で考える話を、上記リンクでご紹介しています。
矢印CD=矢印CB+矢印BDですから、矢印CDを回転してみましょう。
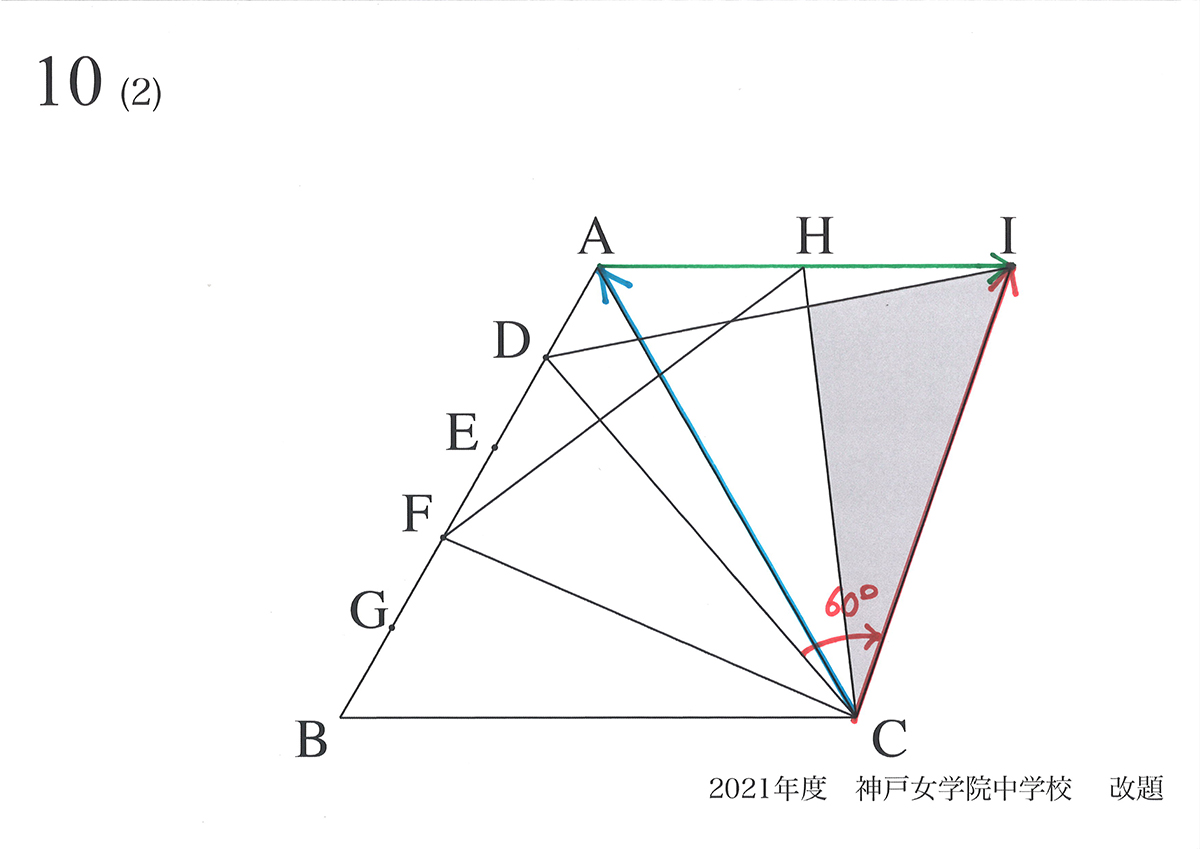
すると、青・緑・赤の矢印は上の図の位置に移動します。
(1)と同じように、Iの位置が決まります。
少し複雑な図形問題ですが、(1)と同じように考えれば出来るはずです。
・「似た作り方」の複数の図形が登場して、図形が「複雑に見える」時は元の図形の性質を考える
・「似た作り方」の複数の図形に対しては、「似た考え方」が出来るはずと考える
・「違う問題」と考えず「似た解き方」を考える
(1)と同様に「矢印の考え方」で正三角形IDCを考えましょう。
面積が分かるためには「何が分かれば良いか」を考える
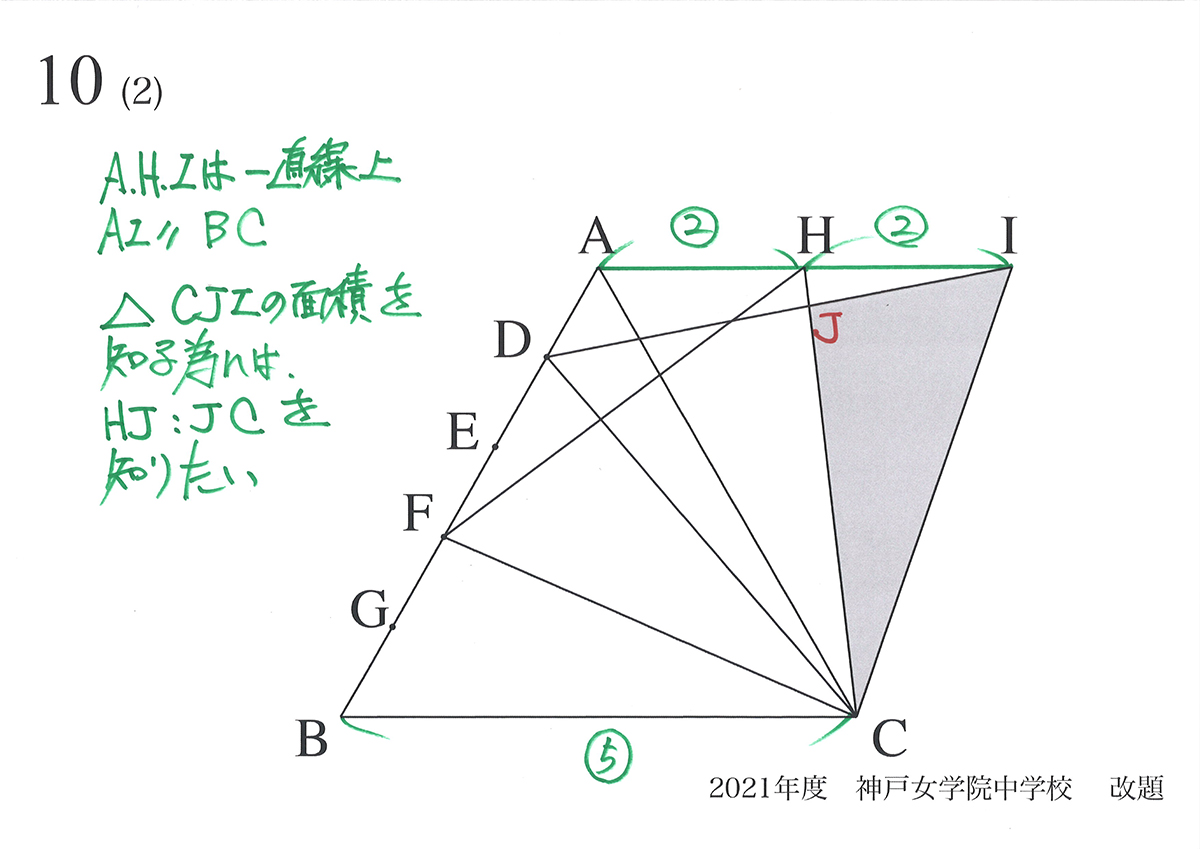
大事な「鍵」をしっかり考えましょう。
A,H,Iは一直線上に並び、「AIとBCが平行」であることがわかります。
「FがBDの中点」であると同様に「HはAIの中点」であることがわかります。
 男子小学生
男子小学生ここまで分かれば、
あとは、少しずつ出来そう・・・
ここからは、相似形を考えてゆきます。



何と何の比が、
分かれば解けるのだろう?
「何を考えるれば、解けそうか」を明確に考えるようにしましょう。
・「問題を解くには、Aが分かれば良い」という「Aを考える」姿勢
・「Aを知るためには、どのようなことが分かればよいか」を考える
・少しずつ、着実に答えに近づいてゆく姿勢
他の問題でも同様ですが、算数は「答えにしっかり近づいてゆく姿勢」が大事です。
一生懸命考えても、「答えに近づいていない」では解けるようにならないのです。
・答えにしっかり近づいている・方向性を確認
・「〜が分かれば良い」と目標を明確にする
いくつか面積の求め方があります。
ぜひ自分で手を動かして、しっかり求めてみましょう。
(1)と同様に、図形の外に飛び出してみましょう。



こうかな?
いや、これかな?
自分で相似形を作ってみたり、探してみましょう。
すぐに答えを見ないで、この「自分で試行錯誤する」ことが非常に大事です。
補助線はフリーハンドで良いです。



なかなか綺麗に線が
引けないんだけど・・・
少し長い補助線になりそうだったら、定規を使っても良いでしょう。
具体的解法は、次回ご紹介します。
次回は下記リンクです。




