前回は「複雑な図形問題の大事なポイント〜正三角形・同じ考え方の図形に共通する性質・正三角形HFCと正三角形IDC・面積が分かるためには「何が分かれば良いか」を考える・問題10(2)解法〜」の話でした。
問題10（再掲載）
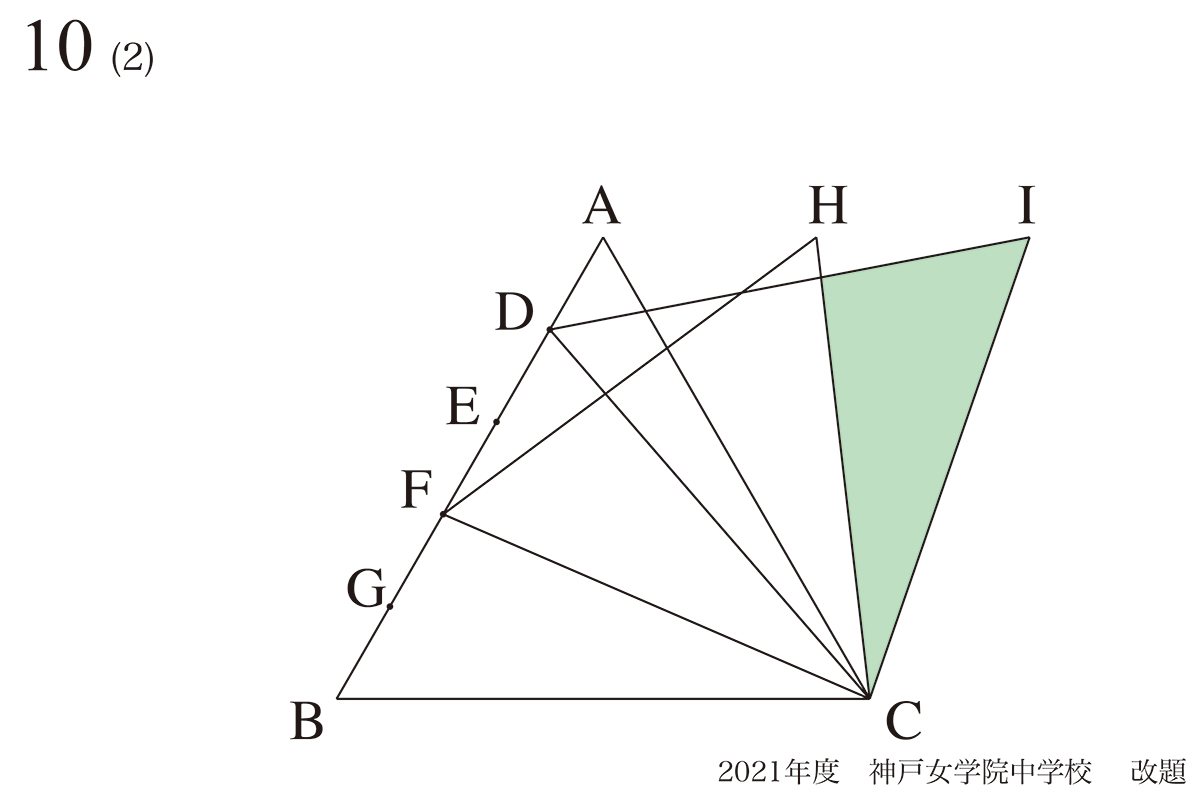
相似形を見つける：平行な線に注目
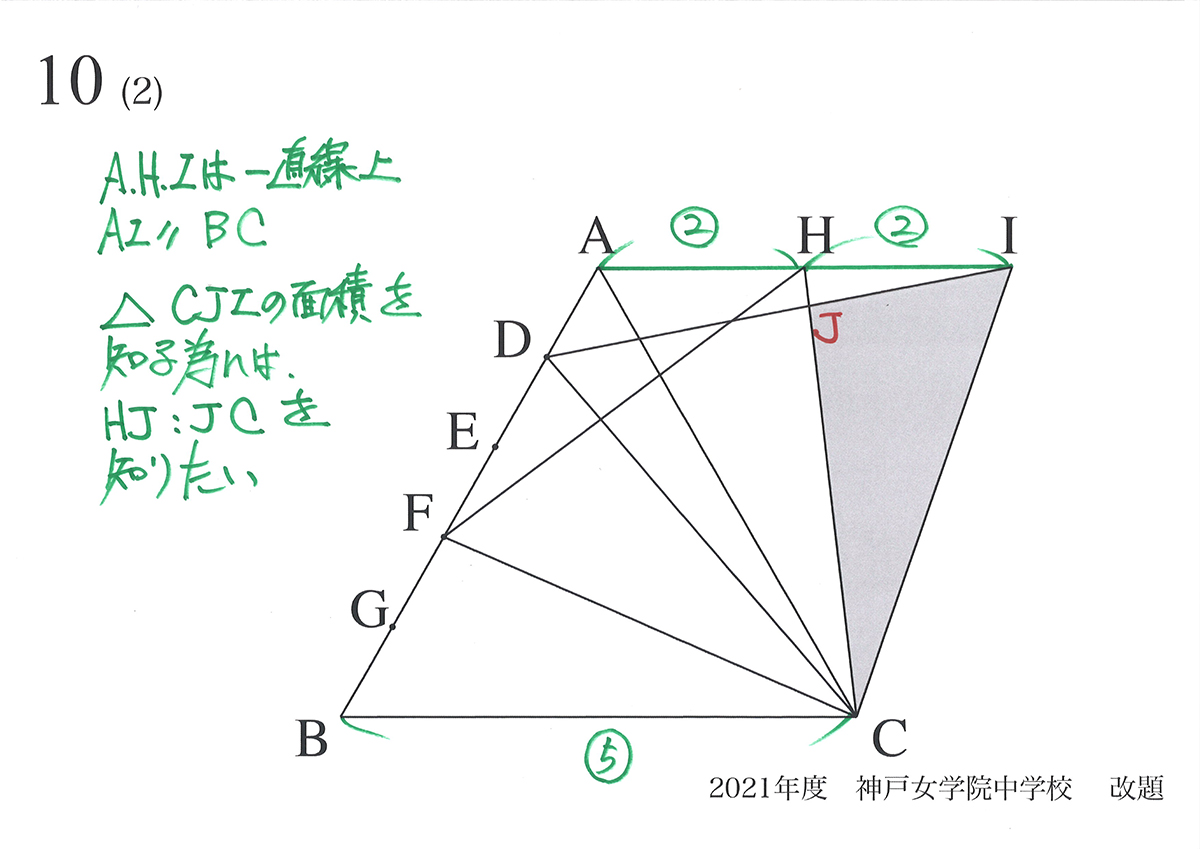
HJ : JCの比を知りたいのですが、「図形の中で相似形」が、なかなか見当たりません。
相似形が見つからないと、
解けないよ・・・
これまで分かっていることで大事なことは、「AIとBCが平行」であることです。
平行な線が一組あると、相似形がたくさん見えてくる傾向があります。
平行な一組の線に対して、異なる線があるとき「相似形ができやすい」のが大きな特徴です。
それは分かっているけど、
相似形が、見つからない・・・
「平行な線があれば、相似形は必ずある」と考えましょう。
そして、自分で図形の外に出て行って、世界を広げましょう。
手が止まってしまっている方は下記の記事を読み直して、再度トライしてみましょう。
相似形が見つからなければ自分で「相似形をつくる」
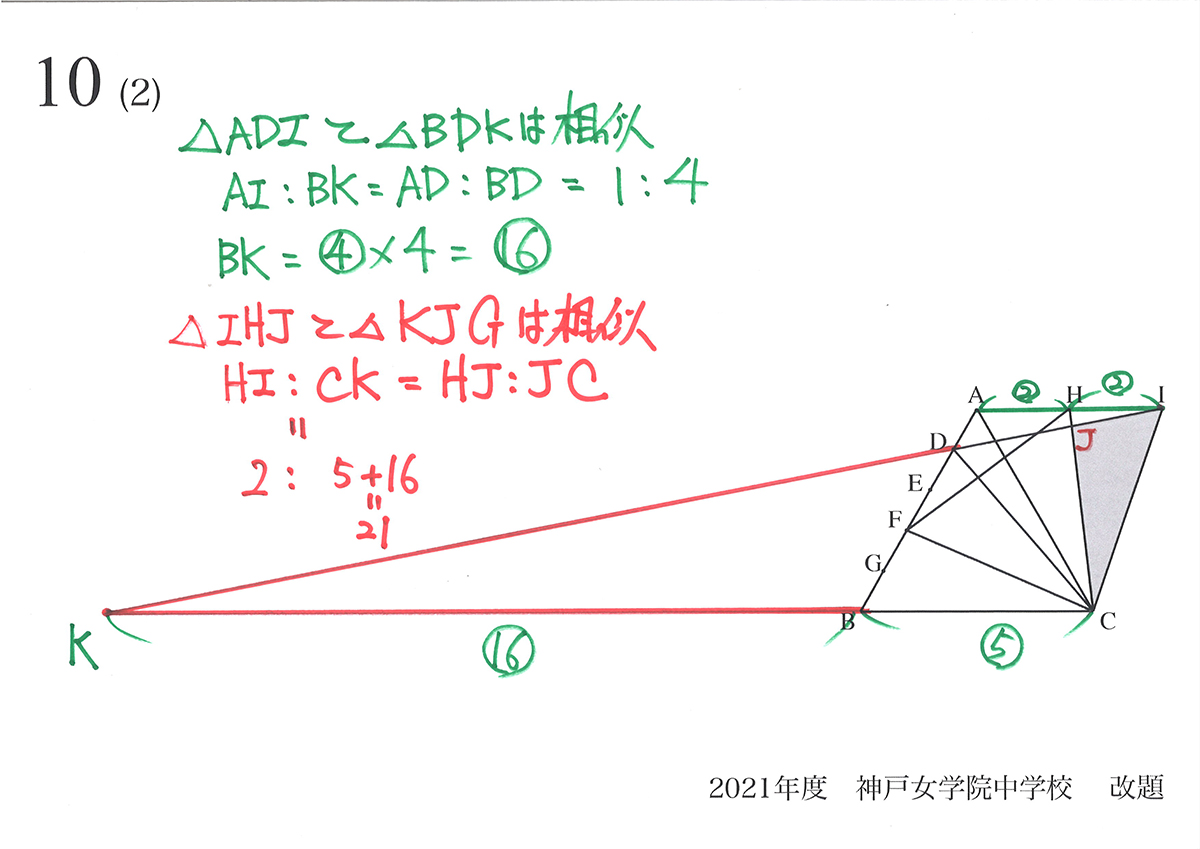
(1)に比べて、かなり大きく外に出てしまいます。
下図のように、IDとCBを延長した交点Kをつくります。
かなり大きく外に出たので、元の図形を小さくして描きました。
こんなに
遠くに線を延長して良いの？
大変そう
だけど・・・
慣れれば、少し図形の外に大きく出ても「感覚的に分かる」ようになるでしょう。
「しっかり分かる」状況になるまでは、こういう図形は省略せずに、大きな紙に描いてみましょう。
一度でも良いですから、実際に描いてみましょう。
すると「相似形が、ありありと分かるようになる」でしょう。
ちょっと
大きいけど・・・
実際に描いて見ると、
確かにわかる！
この「描いてみて、頭でパッとイメージ出来るようになること」が大事です。
このように「平行な線がある」場合は、「必ず相似形がある」と考え、なければ作りましょう。
・「相似形が必ずある」と考えて、相似形を探す
・相似形が見つからないときは、「相似形を作って考える」姿勢
問題を解く勘を磨く：「遠回り」や「無駄」から分かること
ちょっと大きすぎかな？
違うかな？
本当にこれで
良いのかな？
と、思った方が、いらっしゃるかもしれません。
実際の入試では、「図形などを拡張しすぎると時間がかかる」可能性があります。
そのため、上のように「外に大きく出る」図形は省略して考えられると良いでしょう。
でも、手が止まっているよりは良いかもしれません。
いずれにしても「どんどん描いみて、相似形を探してみる」姿勢が大事です。
自分で描いた「補助線」や「図形の外に出てみる」が「解にたどり着かない」可能性があります。
「正解に辿り着く」意味では、こういう行為は「無駄」になります。
あっ・・・
出来なかった・・・
答えにたどり着かないから、
無駄になっちゃった・・・
あるいは「遠回りな考え方」になることもあるでしょう。
「本質的思考力を鍛え、学力を上げる」ためには、「無駄なこと」「遠回りな考え方」が最も大事です。
無駄なことを実際にやってみると、「図形問題の補助線などの勘」が磨かれてきます。
その意味では、「無駄なこと」は「無駄ではなく、学力が大きく上がっている」のです。
・解答に至らない「無駄なこと」が大事
・「遠回り」や「無駄」を経験すると、試験で「何が大事か」の感覚が磨かれる
こういう「勘」は参考書や問題集をいくら眺めていても、なかなか身につくものではありません。
「自分で考えて、試行錯誤する過程」で身についてゆくものです。
そして自分で考えて、自分の手を動かしたことは、大事です。
一生懸命参考書や問題集を読み込むよりも遥かに身について、「本当の学力」になってゆきます。
他にも考え方はありますから、自分で色々と考えてみましょう。
明日、解法をお知らせします。
