大事な答案への姿勢〜「大体でも書く・描く」姿勢・分かることはハッキリ表現・問題に取り組む順序は「受験生の自由」・走り書きやメモを書く・端的に表現〜｜中学受験・高校受験・大学受験・算数・数学

前回は「合格の可能性の伸ばし方〜試験終了間際に解法に気づいた時・試行錯誤の痕跡を描く姿勢・考えていることは、どんどん書く：懸命に取り組む姿勢・学校側が欲しい人材へ・「積極的に書いて・描く」姿勢〜」の話でした。

「大体でも書く・描く」姿勢：分かることはハッキリ表現

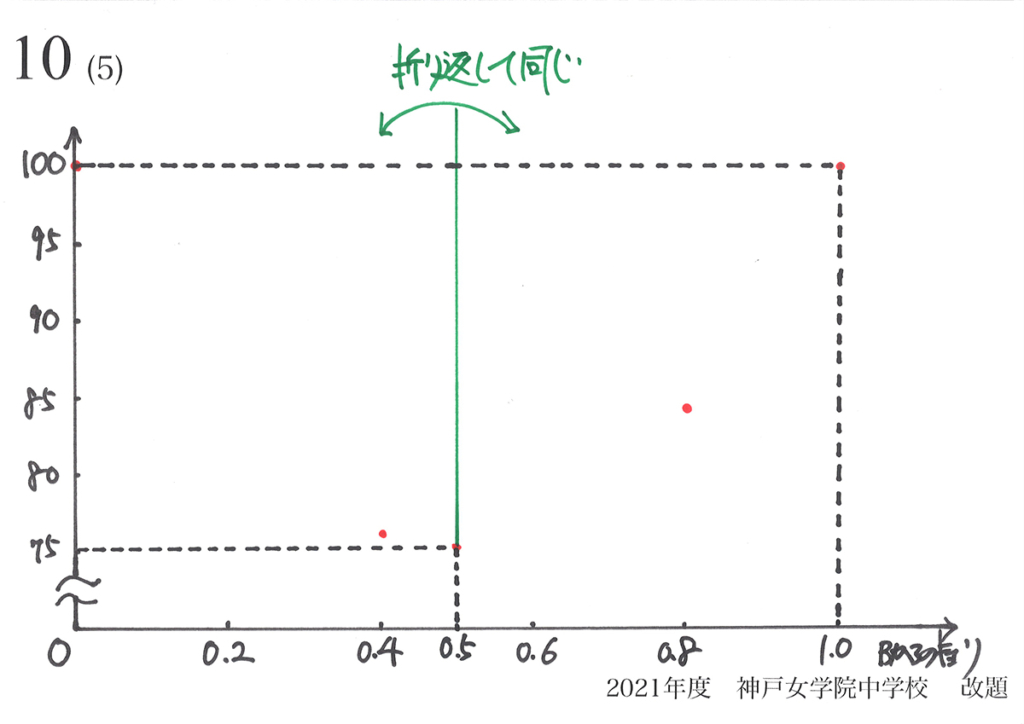
算数実践で、「グラフの大体の形（概形）」を考えました。（上記リンク）

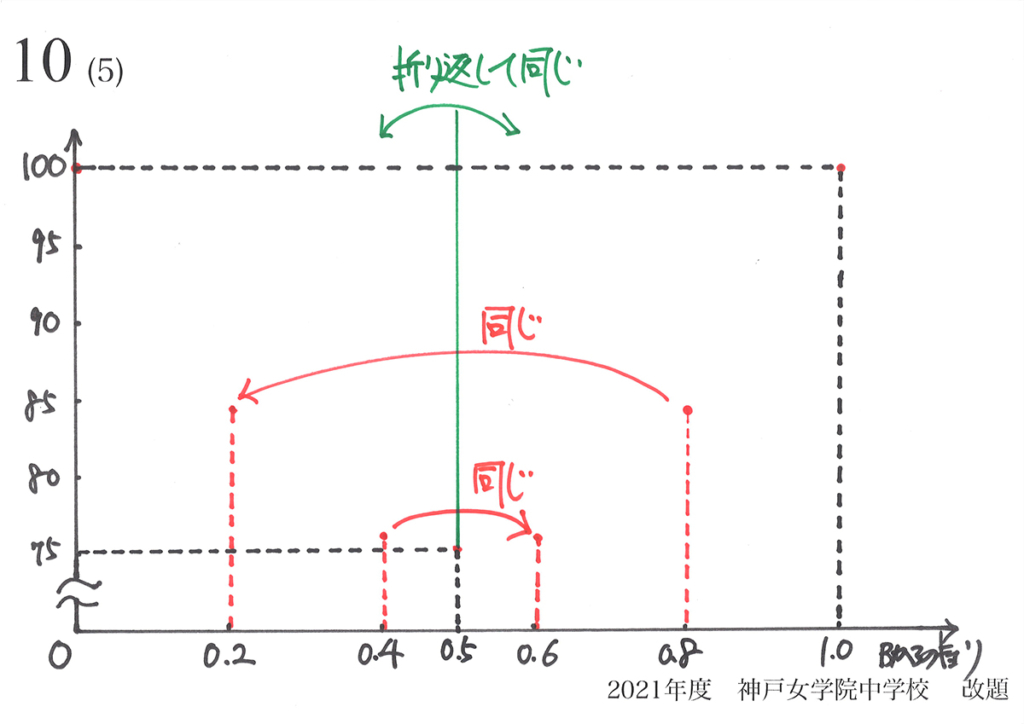
(1)(2)の寄り道（上記リンク）で考えた「二つの点の面積」が、小問・誘導問題としてある場合を考えます。

そして、最後に、

「グラフを描く」問題と仮定します。

このように「グラフを描く」問題は中学受験では少数ですが、考えてみましょう。

高校受験・大学受験では、「グラフを描く」出題は結構あります。

ここで、残り時間が少ない時、

そういう時は、特に記述式の場合、何か「分かっていることは表現する」ことが大事です。

面積が先なので、

「まずは面積」が、一つの方法です。

ここで、「面積を求めるより、グラフを優先する」考え方もあります。

「だいたいのグラフの形はわかりそう」という時。

そういう時は、面積の問題を飛ばして、最後のグラフの問題に取り組みましょう。

そして、分かるところまでハッキリ表現しましょう。

問題に取り組む順序は「受験生の自由」

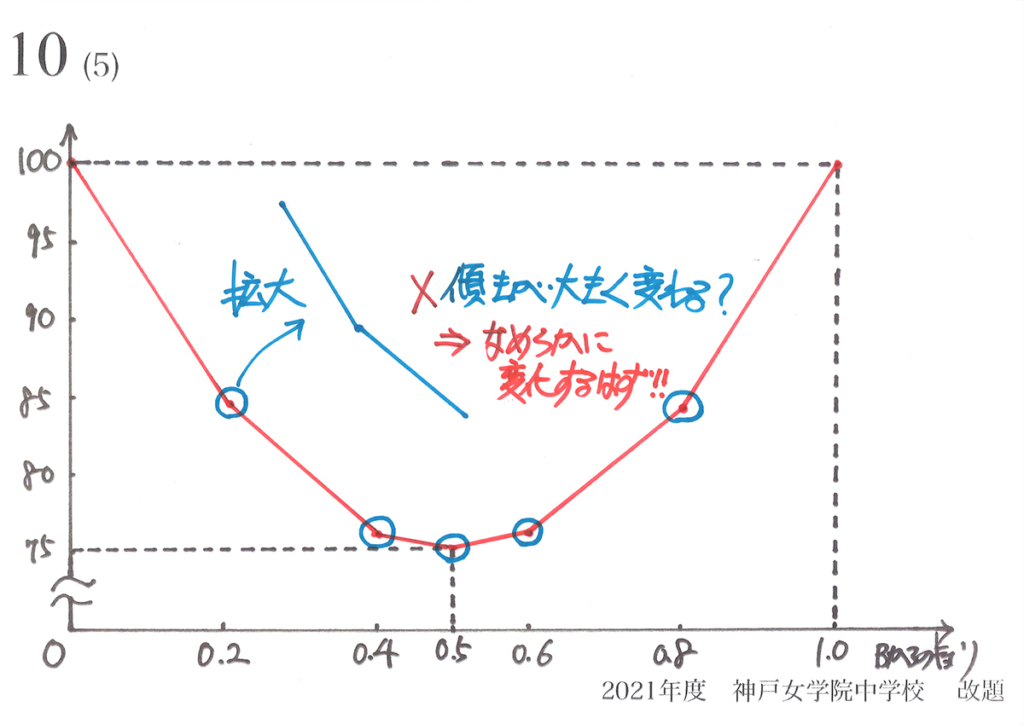
普通に考えれば、「面積を求めて、しっかりプロットしてグラフを描く」です。

それを「面積を求めずに、大体のグラフを描く」時、

「飛ばしたらダメでは」と感じる方もいるかもしれません。

「答えのみ」でも「記述式」でも、先の問題をやっても問題ないはずです。

問題文に、

このような記載あれば「解く順序を変える」のは良くないですが、これは書いてないでしょう。

筆者は、このように「解答する順序を規定した試験」を見たことがないです。

そもそも算数・数学において「出題者が考える順序」を固定する発想は、非常に良くないです。

そのため、「自分で分かることを先」に解くことは問題がないと考えます。

本来、問題に取り組む順序は「受験生の自由」でしょう。

学校や採点者の考え方では、

このような可能性はあります。

独自のカラーを持つ学校は、

「順序を飛ばして答えたから✖️か減点」は、「絶対にない」と考えます。

問題文に、

このように明記されていれば別ですが、「この記載はないのが、ほとんどのケース」でしょう。

走り書きやメモを書く：端的に表現

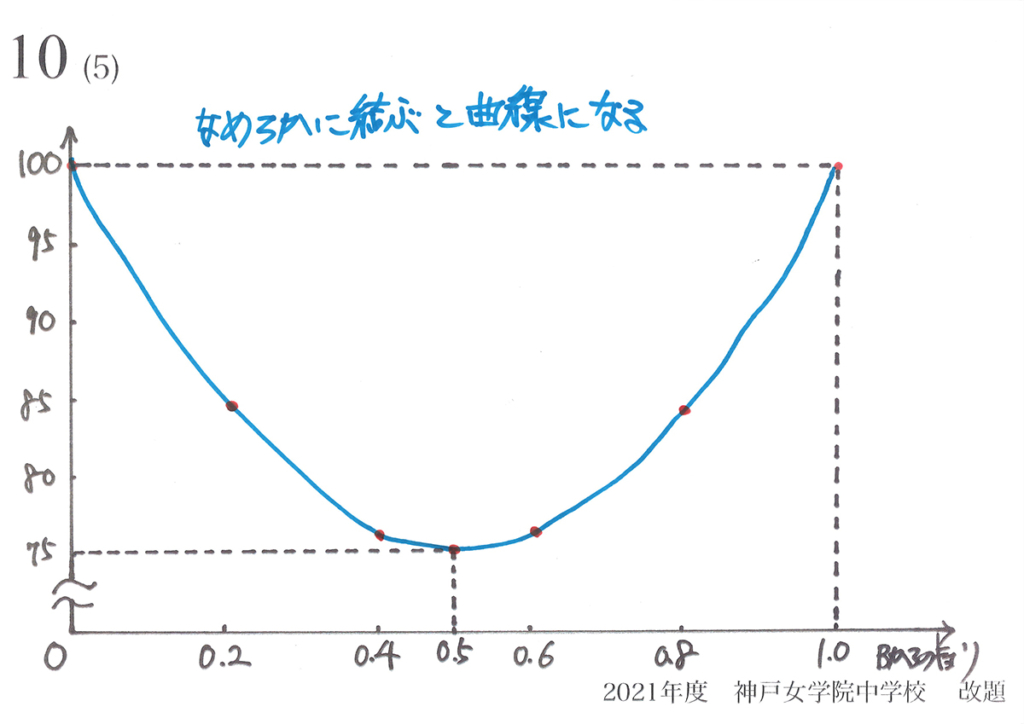
基本的に大問の構成は、「小問の順序通り取り組むのが、解きやすい」構成になっています。

時々、ちょっと分かりにくい誘導形式の小問もあります。

そういう時は、(3)を飛ばして(4)をやりましょう。

状況にもよりますが、「分かること」は明確に書いてゆきましょう。

特に「記述式問題」の出題形式の学校で、

この発想は、絶対にないでしょう。

わざわざ「記述式」にしていることは、

「志望者の学力を深く試験したい」と、学校側が考えているからです。

上のグラフを描く例で、具体的面積の数値を飛ばして、グラフのおよその形を描いた時。

このように「分かっているところまでは採点」となるでしょう。

記述式であれば、走り書きでもメモでも「分かっていること」を書くことは大事です。

「ちゃんと書く」方が良いですが、それにこだわらないようにしましょう。

上のグラフの例なら「対称だから」とか「なめらかにつないで」とか端的でも良いでしょう。

この「端的なこと」は、算数・数学的には非常に本質的であることが多いです。

そうして「本質的なこと」が少しでも表現されていれば、

きっと、採点者は「相応に評価して、採点してくれる」でしょう。

自分なりに「自信持って分かること」は、大事なことです。

それは問題の順序に関係なく、しっかり表現して解答してゆきましょう。

日頃の勉強の際でも、このようにメモや走り書きでも書いてみると、

「書く・描くと気づくこと」があるでしょう。

こうした「自分なりの気づき」を重ねると、大きく学力がアップします。

特に記述式の試験を課す学校を志望校とする人は、日頃から、立式などをしっかり書くと良いです。

「自分の分かることをハッキリ表現する」ことが、合格への道です。

次回は下記リンクです。