前回は「整数問題のコツ・ポイント〜「入れ替える」ことを具体的にイメージ・物々交換とコイン・具体例で実験・状況を理解・奇数と偶数・対象を半分にする・簡略化した書き方・採点者へのメッセージ〜」の話でした。
差を考えて小さく分割：対象を小さくする
今回は、算数の全分野必勝法「差を考えて、小さく分割する」の話です。
「入れ替える」を具体的に考える話をご紹介しました。（上記リンク）
男子小学生入れ替えたら、
どうなるかな？
女子小学生「入れ替える」のは
分かりやすいけど、具体的にどうなるかな？
具体的に考えてみることが大事で、入れ替えると起きる「金額の差」がポイントでした。
「硬貨77枚で4,260円」であり、ある2種類の硬貨を入れ替えたら3,900円になりました。
ここで、差の4,260-3,900=360円を考えました。
このように「差を考える」ことは、大事なこと・本質的なことでもあります。
「差を考える」と、対象とする数字が小さくなってゆきます。
男子小学生考える数字が
小さい方が楽だね。
条件を絞る：数字の差と「元の数字」の関係性
4,260円とか3,900円などの合計金額は、比較的大きな数です。
77枚の硬貨でこれらの金額を作るのは、「たくさんのケース」が考えられそうです。
女子小学生たしかに、
77枚もあると・・・
女子小学生たくさんの「お金の合計」が
考えられそう・・・
ところが、「差の360円」となると、急に扱いやすくなります。
ここで、
男子小学生360は50の倍数では
ないから・・・
男子小学生50円玉だけでは、
つくれないかな・・・
「50円玉だけでは差額を作れない」と気づきます。
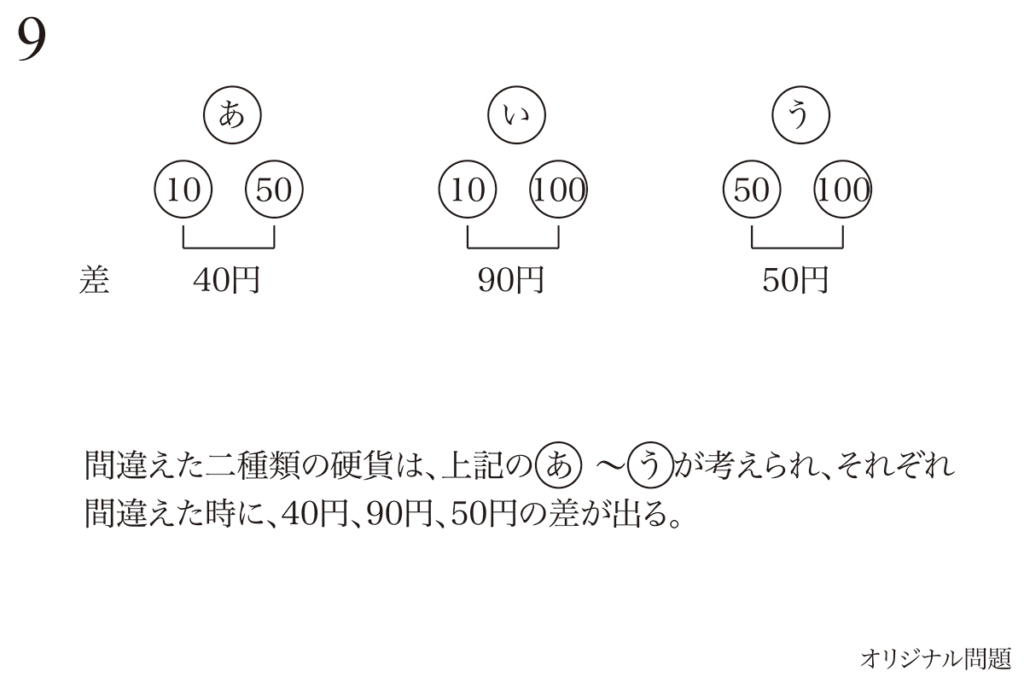
コインが10円玉・50円玉・100円玉と「三種類ある」から難しめである、この問題。
これが、例えば「10円玉と50円玉の2種類」だったら、一気に問題は簡単になります。
電流・電圧・抵抗の「三つが登場する」ため「難しく感じる」電気。
電気の問題では「電圧が主役」です。（上記リンク）
対して、算数のコインの問題などでは「主役は自分で決める」ことができます。
ここで、「あ」と「い」の二つの場合に絞れたら、主役の未知数は自分で選びます。
ここでは、「10円玉の枚数」を未知数として、「10円玉を主役に設定」すると下記のようになります。
状況が二つに絞れれば、だいぶ考えやすくなりました。
数字の差には、「元の数字」と何らかの関係性があることが多いです。
4,260、3,900という「四桁の数字」から360は「三桁の数字」となり、一桁小さくなります。
女子小学生一桁小さくなると、
だいぶ考えやすいね！
考える対象の数が「一桁小さくなる」のは、全然違うことです。
小さい数字は、考えるのが比較的簡単です。
差が変わる場合と変わらない場合：流水算・年齢算
上記の場合は、「入れ替えた結果」差が生まれます。
「Aさん、Bさん、Cさんがいて、今の年齢は4:3で、5年後には〜」のような問題もあります。
この問題を考えるとき、大事なことは「年齢差は変化しない」ことです。
男子小学生年齢の「差は変わらない」のが
ポイントだね！
「変化しない数・量」に着目すると、問題がスッと解きやすくなる時があります。
流水算で「川下から川上に向かうAさん、Bさん」がいる問題を考えましょう。
「川下から川上に向かう」にはAさん、Bさんともに川の流れで速さが小さくなります。
川下→川上の速さの差は、もともとの「AさんとBさんの速さの差」と同じです。
同様に、川上→川下では速くなりますが、その速さの差も「AさんとBさんの速さの差」と同じです。
女子小学生「流水算は、こう解く」って
考えていたけど・・・
女子小学生「差が変わらない」と
考えると、視点が広がるね！
・「変化しない数・量」に着目
・「和や差、比が変わらない」などに着目して解く
流水算はこのことに着目して、絵やグラフを書くと一気に解きやすくなります。
「差を考えること」は大事なことで、大きなものも小さくすると考えやすくなります。
流水算・年齢算の問題などに取り組む際は、
男子小学生あっ、この差が
ずっと同じだ。
女子小学生ここの差が
変わらないから・・・
「変化しない速さ・数・量」に着目してみましょう。
速さの問題などでも、「変わらない差」に着目すると、解きやすくなることがあります。
このように学んでいる際に「総まとめ」してみると、様々な考え方や解法が結びついてゆきます。
男子小学生この問題は、
これとこれの差に注目するのが大事・・・
特に秋から直前期にかけては、「この問題はこの解き方」ではなく、「大事なポイント」を重視して、
女子小学生自転車とバスの速さの
差が一定だから・・・
女子小学生このグラフは、
こういう状況だね・・・
問題をじっくり解くと、総合力が上がるでしょう。
次回は下記リンクです。
