前回は「てんびん算と食塩水の濃度〜実社会と「てんびん算」・「なぜ？」の理解・「算数（数学的）コンセプト」と実生活・子どもと一緒に親も学ぶ機会・子どもと接する貴重な時〜」の話でした。
てんびん算の「つり合っている」イメージ
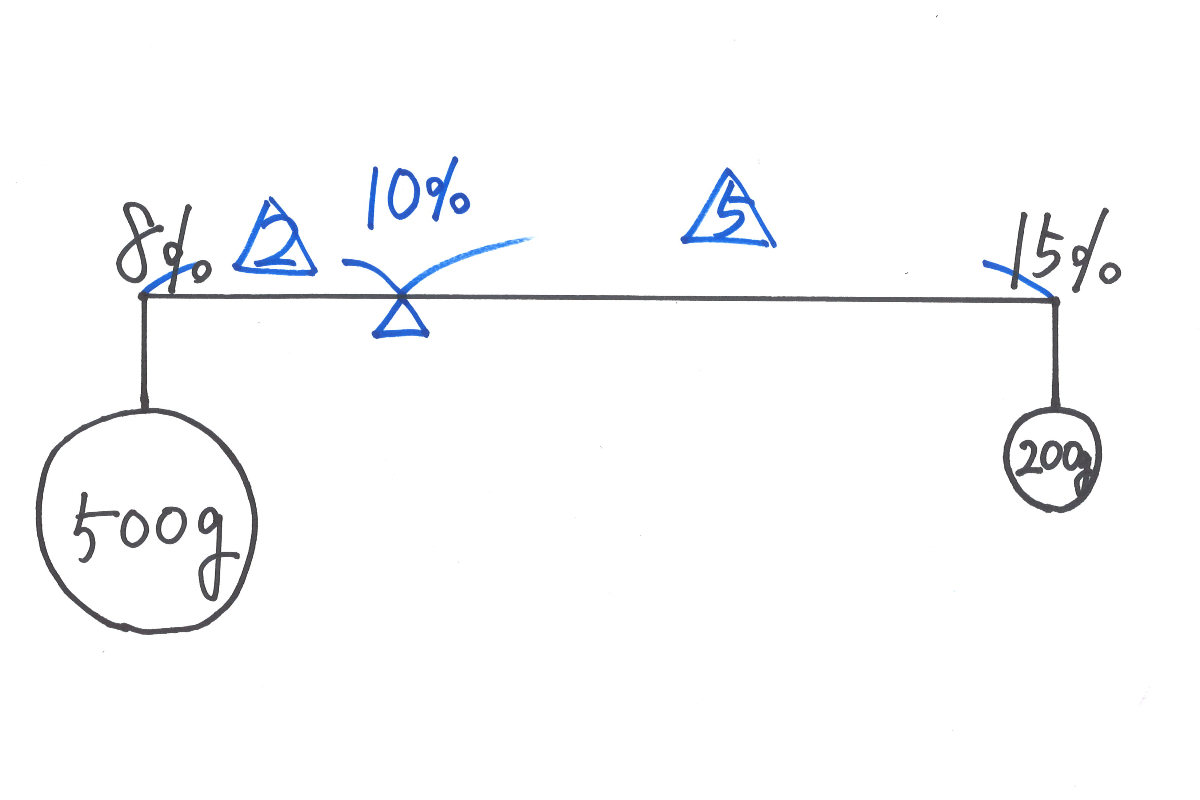
今回は、てんびん算を、別の視点からの問題を考えたいと思います。
以前は、2つの食塩水を混ぜた時「濃度が何%でバランスがとれるか？」という視点でした。
今回は混合後に釣り合う・バランスする濃度がわかっています。
そして、混合する片方の食塩水の濃度を考えます。
食塩水A：濃度は不明、240g
食塩水B：濃度20%、600g
を混ぜたら、濃度16%の食塩水840gとなりました。
食塩水Aの濃度は何%ですか。
てんびん算で考えます。
てんびんが釣り合っているイメージを描きます。
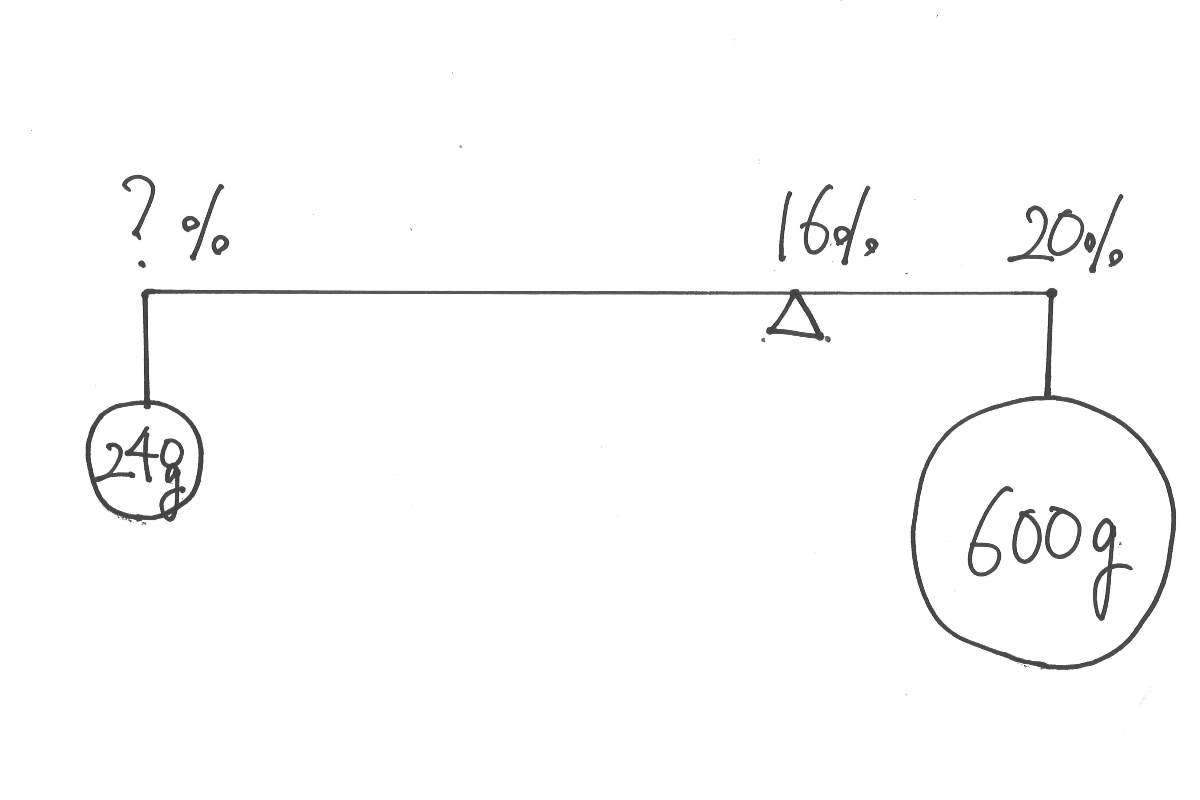
まずは、この「回転する力（モーメント）」がつり合うイメージが大事です。
「右回りの回転する力（モーメント）」と「左回りの回転する力（モーメント）」が同じイメージです。
分からない濃度や重さは「？」と書きましょう。
？でいいの？
①とかにしなくていいの？
①などの未知数にしても、自分の好きなように書いてみましょう。
それらの
回転する力（モーメント）が、
釣り合うんだ・・・
というイメージです。
そして、てこの原理です。
重さが「240g：600g=2：5」なので、つりあいは、「逆比の5：2」で取れます。
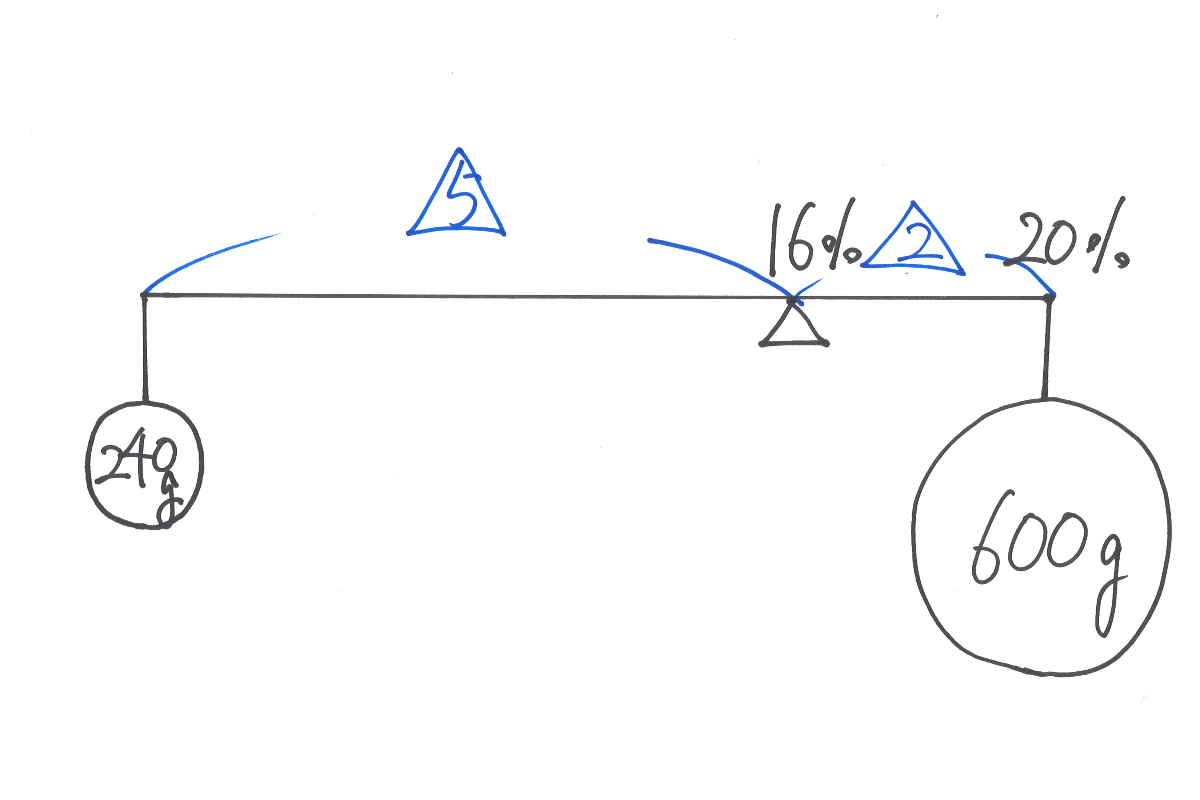
「なぜ？」と物理的発想を育む姿勢：「逆比」などをしっかり理解
この時「逆比になる」ことを、丸暗記するのは避けましょう。
なぜ、逆比になるのでしょうか？
「掛けたら同じ」に
なるから、だよね、
「てこ・ばね」や「電気・電流」などでも出てくる「逆比」。
ただ「逆比になる」と暗記していると、応用力が育ちにくくなります。
「なぜ、逆比になるのか？」などの理由は、しっかり理解するようにしましょう。
ここで、20%-16%=4% が長さの2に当たるので、下記のようになります。
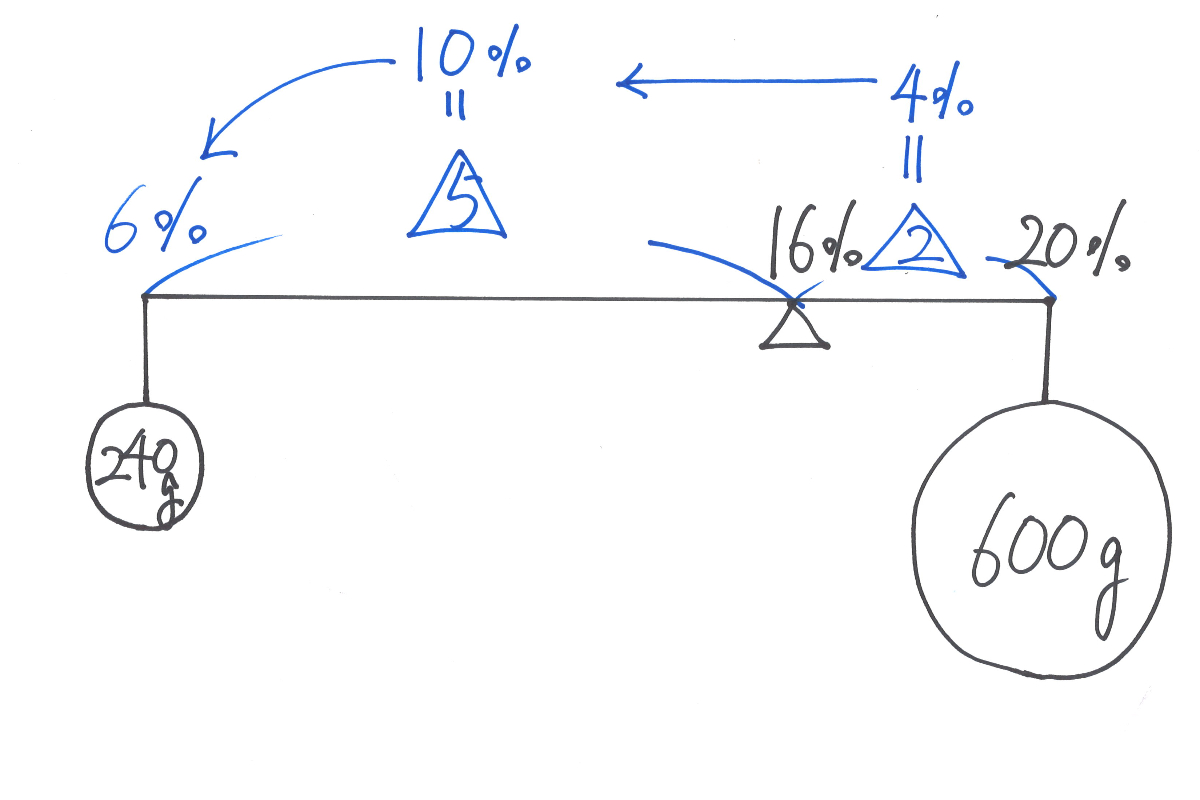5の長さは 4/2×5=10% となりますので、食塩水Aの濃度は
16-10=6%
となります。
全く同じ考え方ですが、別の視点からの解法となります。
大人から見れば「当たり前」ですが、子どもにとっては新鮮味があるでしょう。
別の視点や別解を考える大事さ
このように「同じコンセプト・考え方を異なる視点から考える」ことは、とても良い勉強になります。
色々な視点で考えてみましょう。
別解を考えたり、学ぶことも非常に良い勉強になります。
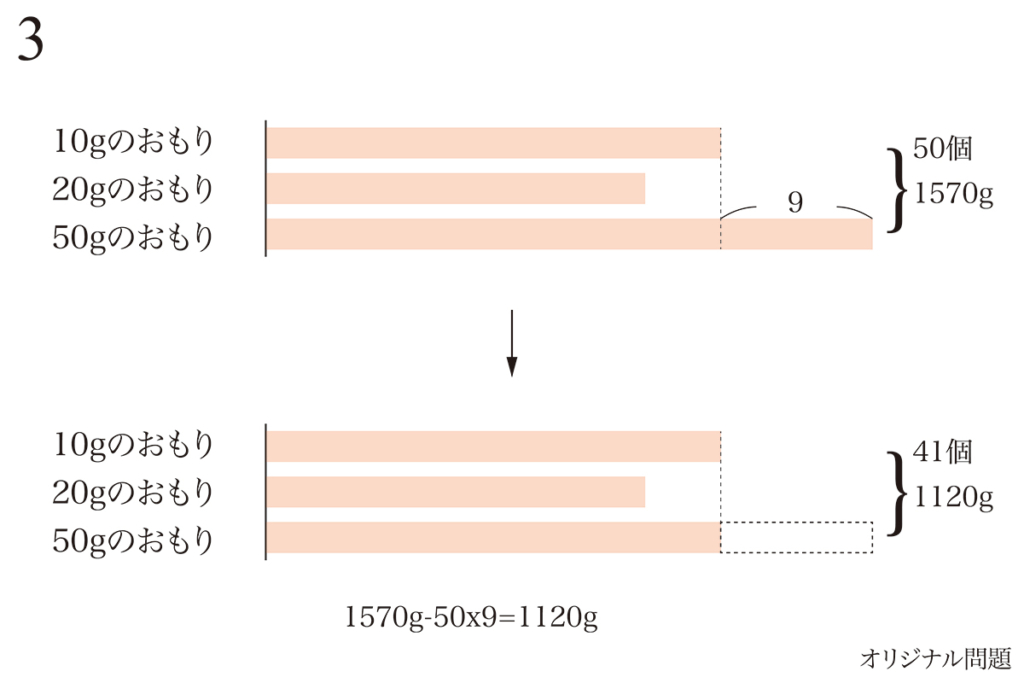
整数問題で二つの考え方をご紹介しました。
これらの考え方は、根本的には似た考え方ですが、視点が異なります。
この「視点が異なる考え方」を学ぶこと。
それによって、「一題から学ぶこと」が「十題から学ぶこと」になるようになります。
このように、「深みのある学び方」は、遠回りなようで近道な学力アップの方法です。
次回は下記リンクです。
