前回は「てんびん算の解き方・平均・逆比〜「なぜ？」と物理的発想を育む姿勢・別の視点で考える〜」の話でした。
「食塩水を混ぜる」とは：食塩水を理解
今回は、てんびん算の応用と「食塩水とは何か？」を考える話です。
「中学への算数2022年7月号」をお持ちの方は、p44をご覧ください。
ここで、筆者の方が食塩水の問題を数式（方程式）で解決しています。
この問題を、てんびん算で考えてみましょう。
そして、この過程で「食塩水を混ぜる」の本質を学びましょう。
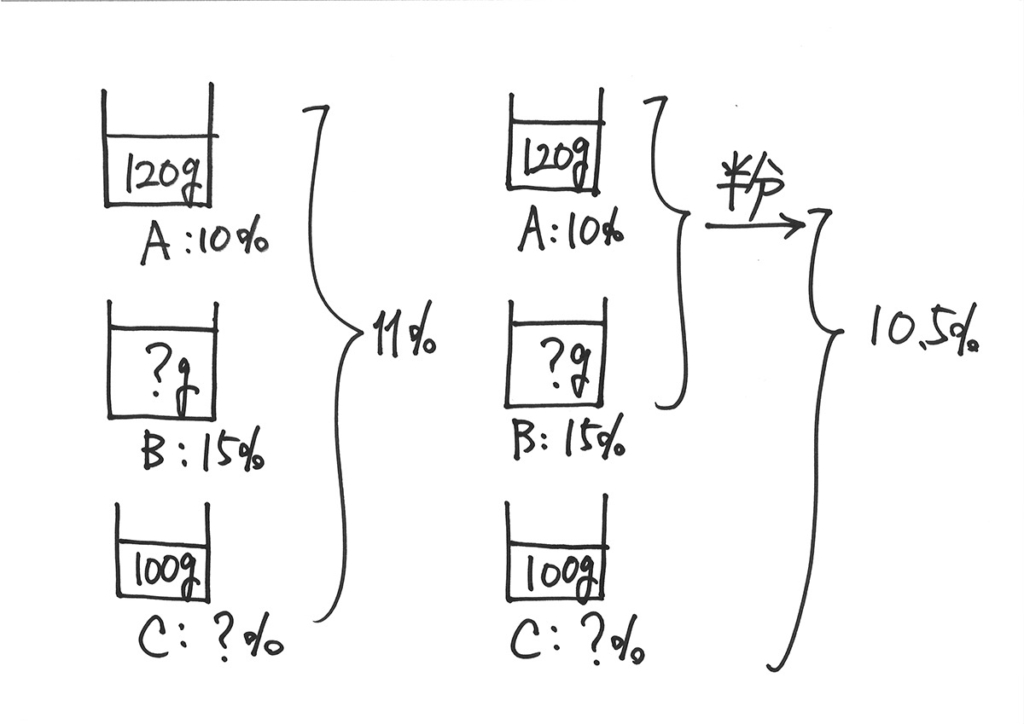
問題の概要は、下記です。
「食塩水を混ぜる」のは、よくある問題ですが、この問題が少しひねっているのは、後の条件です。
「まずAとBを混ぜて、その半分とCを混ぜる」です。
これらの条件を、てんびん算で考えてみましょう。
てんびん算の「つりあい」：3つの食塩水の絵を描く
女子小学生食塩水を３つ混ぜるから、
難しそうだけど・・・
食塩水が２つでも、３つでも考えることは同じです。
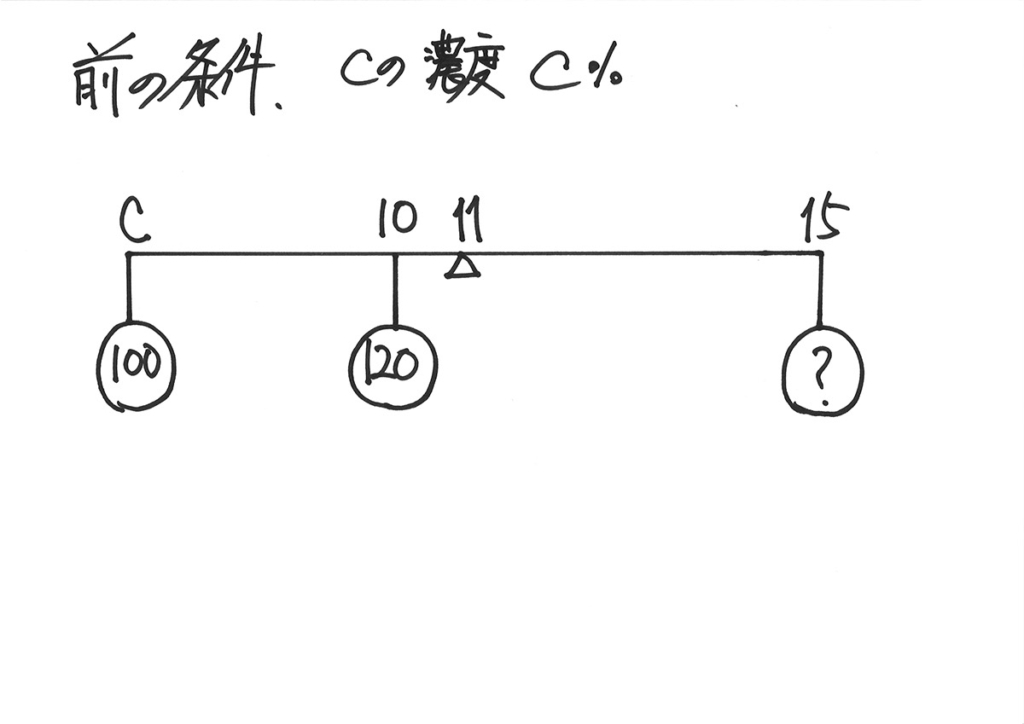
前の条件は「てんびん」に表現できて、これは何か進められそうです。
男子小学生これは、「てんびん」のバランスを
考えられそうだね・・・
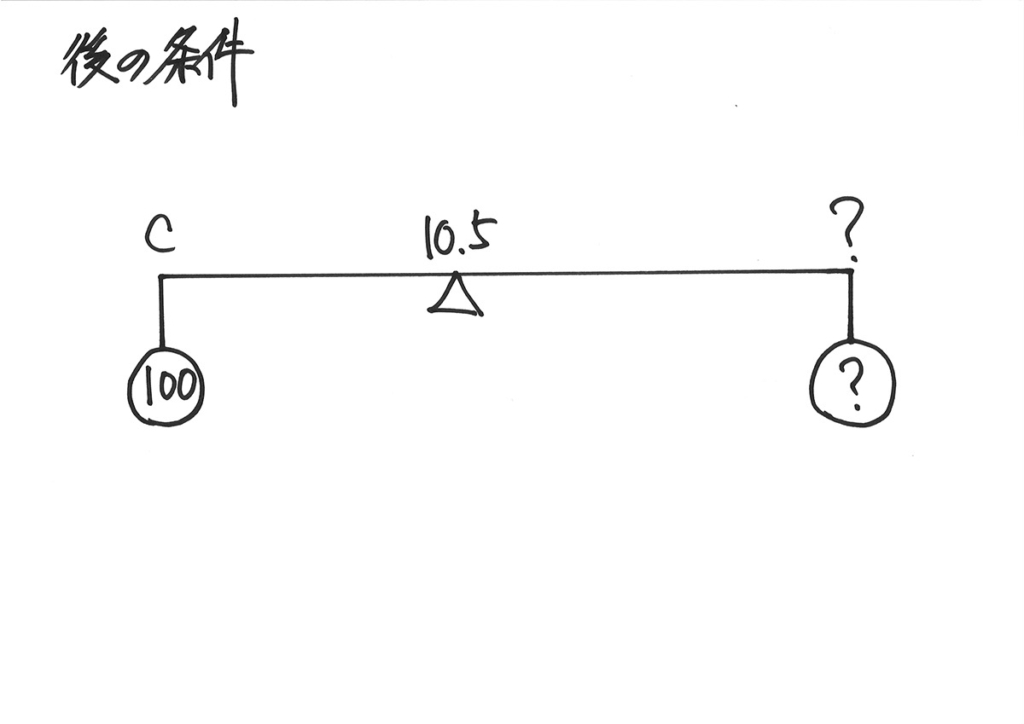
後の条件を考えてみましょう。
男子小学生さっき、３つだったの食塩水が
２つになったから簡単だけど・・・
男子小学生一つは濃度も
量も分からないね・・・
女子小学生これでは、何がなんだか、
分からないけど・・・
濃度も重さも不明では、「てんびんのつり合い」のキッカケがつかめません。
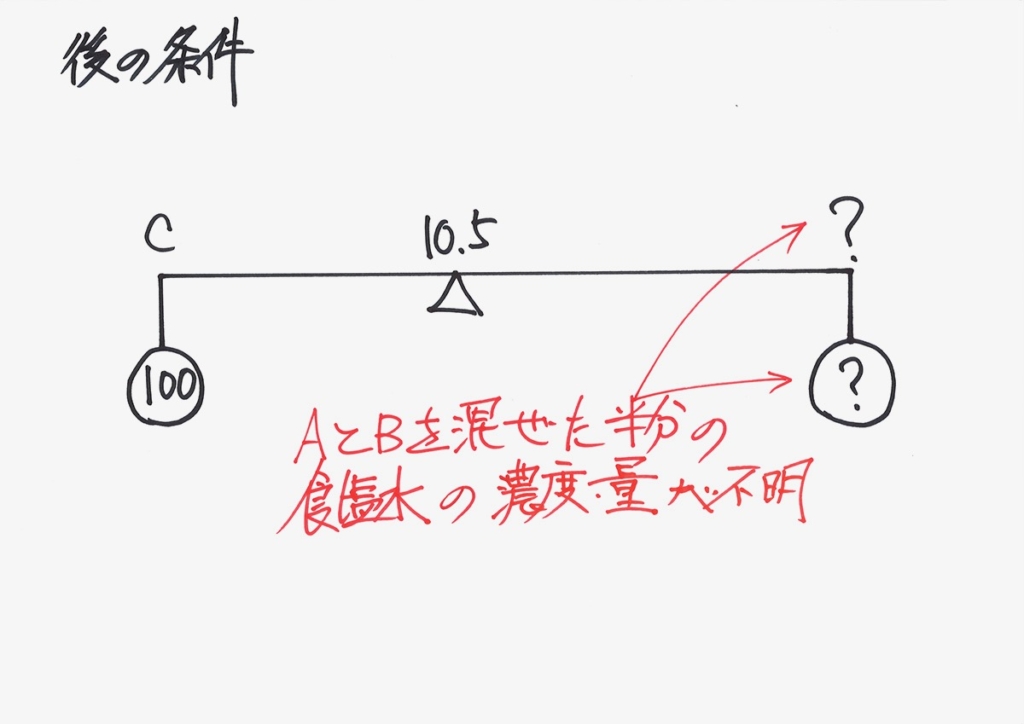
「てんびんでバランスを取る」時は、濃度・量のどちらかがわかってないと、考えようがないです。
食塩水=食塩+水：食塩水を分解
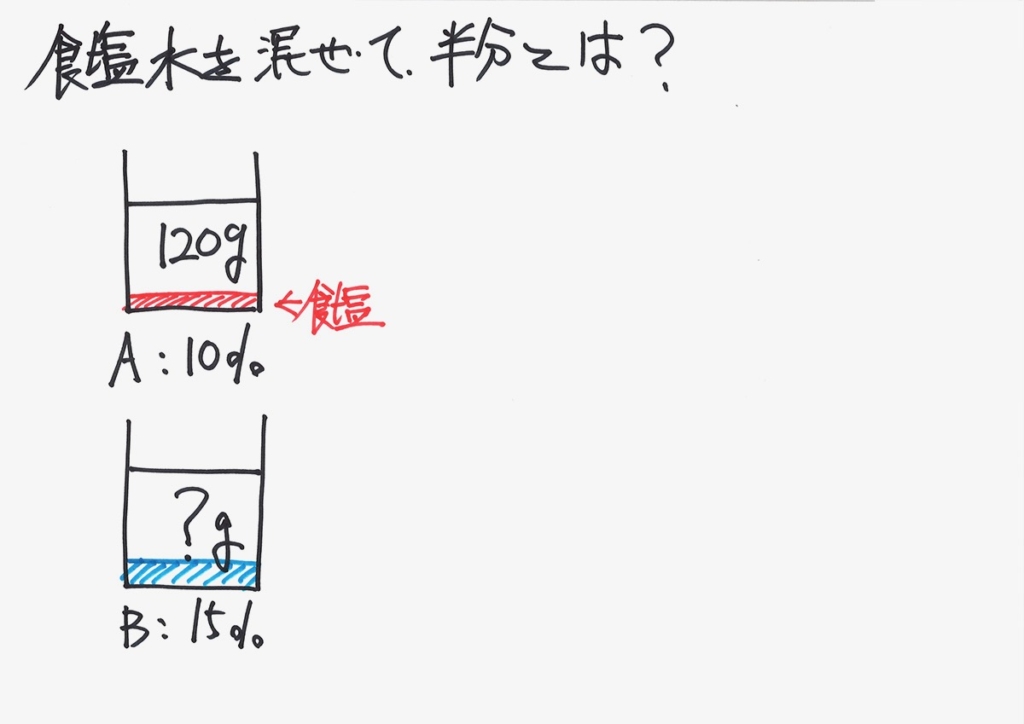
ここで、「AとBの食塩水を混ぜて半分」を、もう一度考えてみましょう。
男子小学生食塩は溶けているのでは
ないの？
女子小学生食塩水だから、
食塩は見えないのではないの？
食塩は溶けて見えないのですが、ここでは、「食塩水の中の食塩」を赤と青で表現しています。
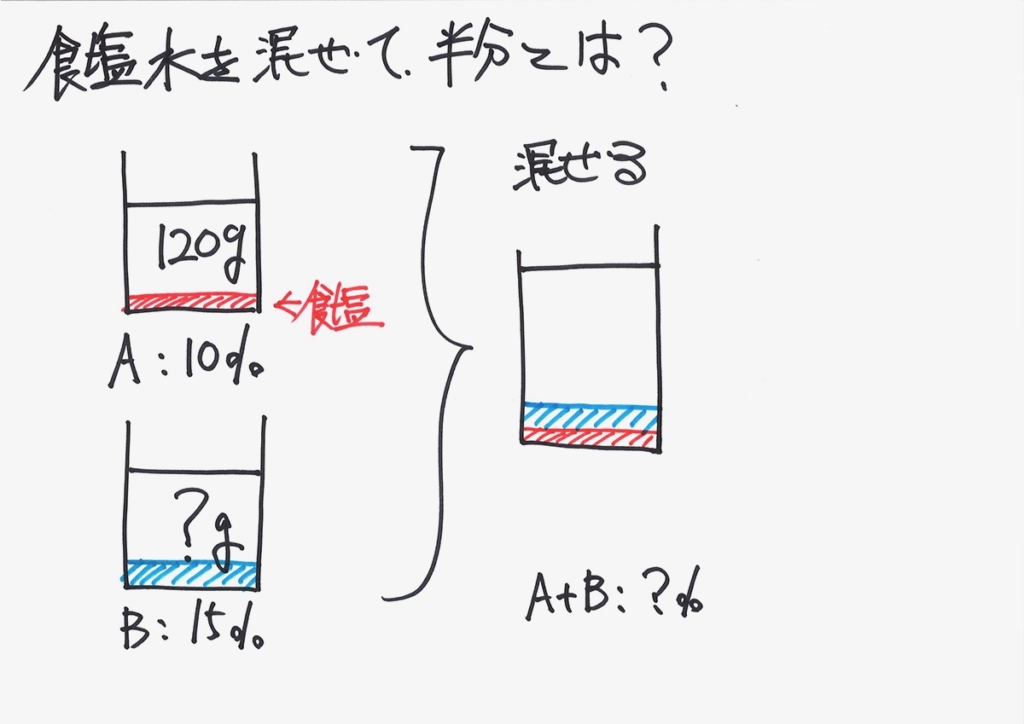
AとBを混ぜると、食塩水が足されます。
男子小学生AとBの濃度が
分かっていたけど・・・
女子小学生混ぜたら、
濃度が分からないね・・・
そして、濃度・量共に分からなくなります。
ここで、大事なことは「混ぜると水も食塩も足しあわされる」ことです。
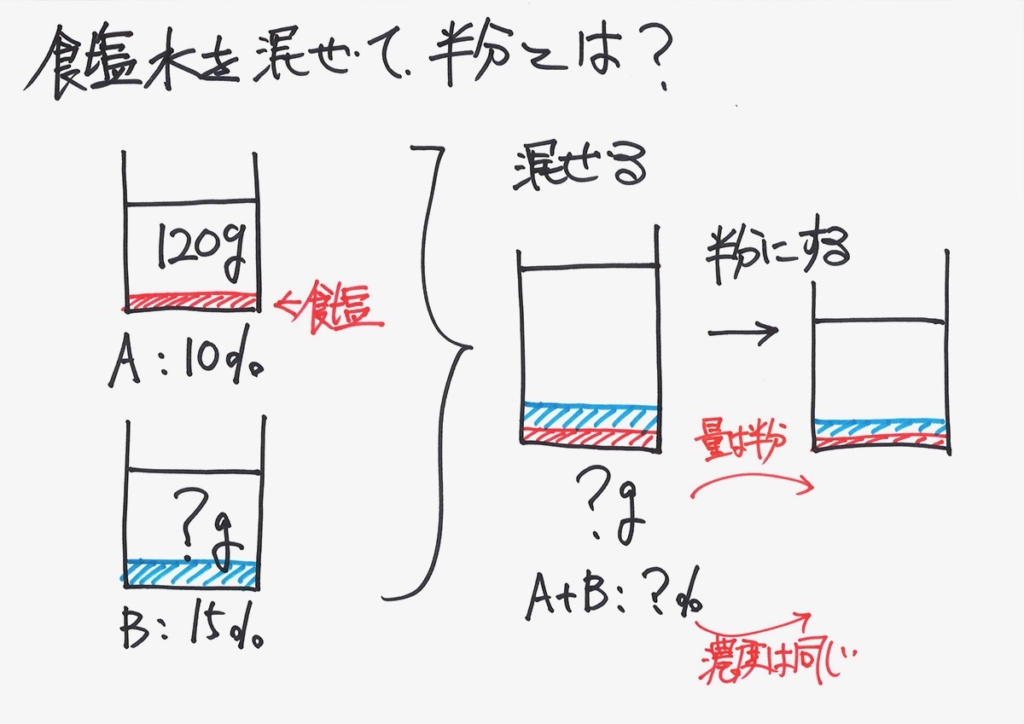
「混ぜて、半分」を考えてみましょう。
すると、「量は半分」で「濃度は同じ」です。
男子小学生やっぱり、
よく分からないね。
女子小学生これでは、
進まない・・・
「混ぜて半分」の過程を、もう一度考えてみましょう。
「食塩水＝水と食塩」ですから、絵を描いて、考えてみましょう。
ここで、非常に本質的なことがあります。
続きは次回にご紹介しますので、少し考えてみましょう。
次回は下記リンクです。
