前回は「模試の判定と第一志望校〜模試の判定が「良くない」時〜」の話でした。
スランプに陥りやすい算数：まずは落ち着いてスランプ脱出
娘が女子御三家中学を志望しています。
先月くらいまでは、算数が得意科目だったのですが、最近成績が落ちてきています。
娘も自信をなくしてきていますが、どのように娘に対応していいか分かりません。
ご意見お聞かせ下さい。
Bさんの親からご質問を頂きました。
ご質問頂き、有難う御座います。
いわゆる「スランプ」と思われます。。
こういうことは「よくあること」なので、気にしすぎない方が良いと思います。
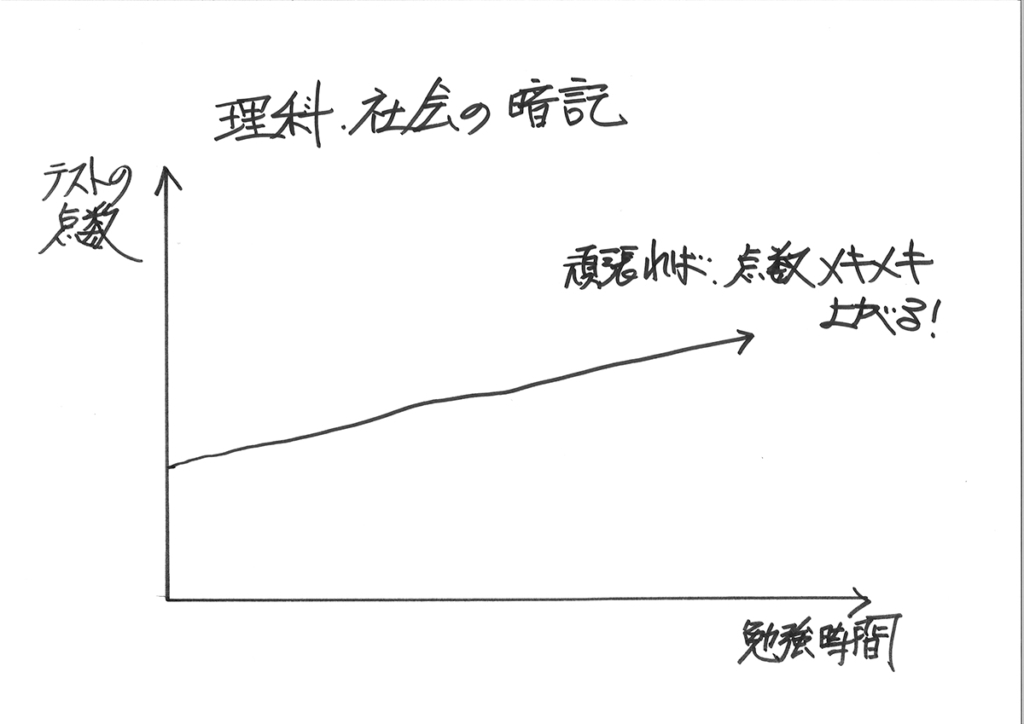
「勉強すれば成績が上がる」傾向が、比較的大きいのが暗記分野です。
そのため、
男子小学生頑張って
勉強したら、社会の成績が上がった！
女子小学生理科の苦手分野を
一生懸命覚えたら、成績上がった！
このように「頑張れば成績が上がる」ことが多いのが、社会・理科（暗記分野）・国語です。
対して、算数は他の科目に比べて出来る・出来ないがハッキリするので波があります。
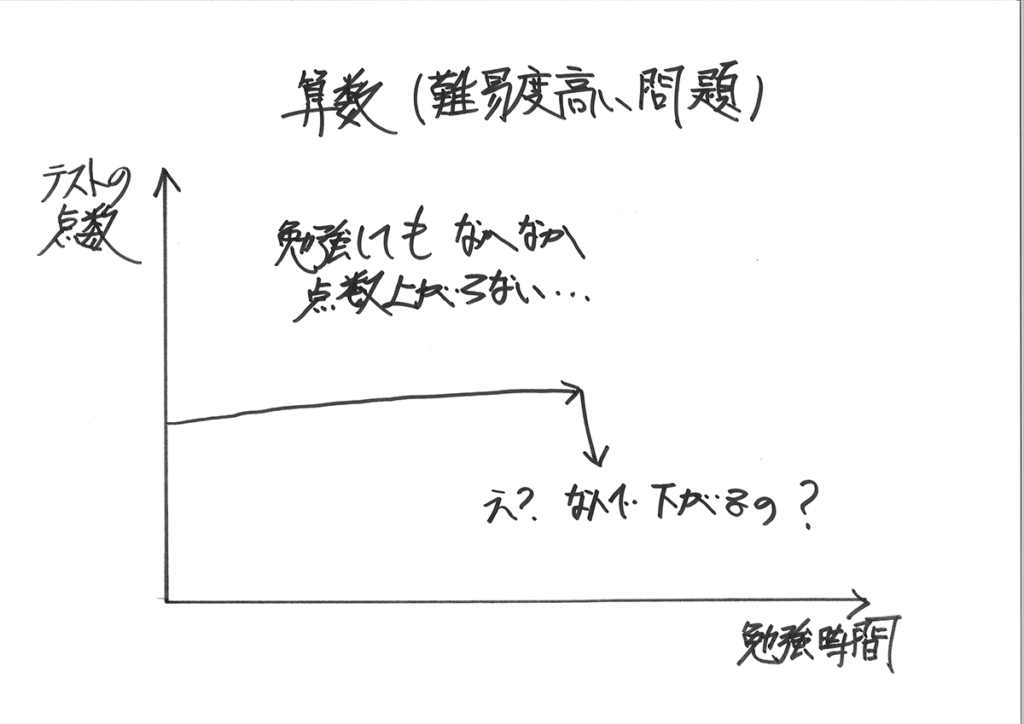
暗記分野では「考えられない」成績の急落が、算数・数学では起こりうる傾向があります。
大学受験においても、こういうスランプを抱える受験生は多いです。
そこで、まずは気持ちを落ち着けることが大事です。
算数の成績アップのコツを、上記リンクでご紹介しています。
落ち着いて、まずはスランプは脱出しましょう。
受験生の母親慌てずに、
じっくり勉強してみよう！
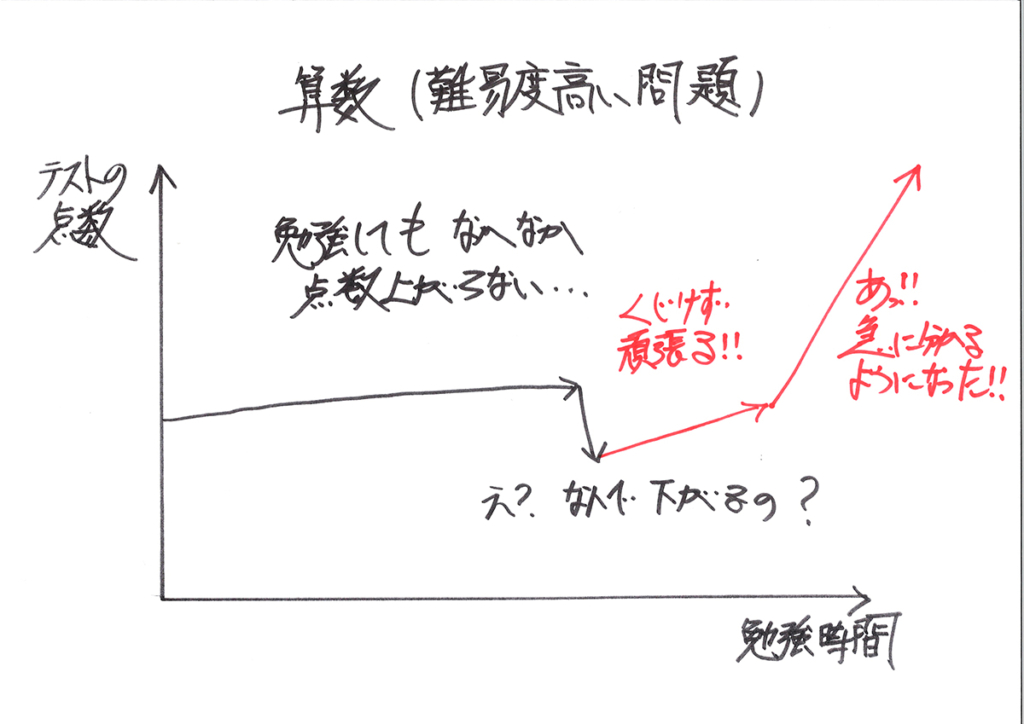
子どもが悲観的になるのは当然なので、まずは親が落ち着いて励ましましょう。
挫けずに頑張ってみれば、再び成績がグッと上がる傾向が起こりうるのが算数・数学です。
受験予定校の過去問やこれまでに取り組んだ問題集で、受験校のレベルに合った問題を復習しましょう。
あるいは、少し易しめの問題を再度取り組んで復習することをおすすめします。
女子小学生少し易しめで
いいの？
女子小学生難しい問題が
解けないで困っているんだけど・・・
難しい問題も、「基本問題の複合」であったり「基本問題の延長」であることが多いです。
まずは、易しめの問題や基本問題を再度復習してみましょう。
算数が「出来ない」「上がらない」時は学んだテキスト総復習
スランプに陥ったり、成績不振になると、
女子小学生新たな問題集で、
特訓しなければ！
このように「新しい問題集」を購入して頑張ってしまう方がいらっしゃるかと思います。
実際に、こういう方が多く、大学受験の時は筆者自も、
武蔵中高生の筆者もっともっと
勉強しよう！
新たな問題集を買い込んだことがあります。
実は、こういう姿勢は「逆効果」になることがあります。
新たな問題集等に手を出すよりも、以前に取り組んだ問題に再度取り組むことが良いです。
まずは、今までやったテキスト・プリント等を総復習して、理解を深めましょう。
これは、子ども本人の個性次第です。
新たな問題に取り組んで、
女子小学生やっぱり
出来ない・・・
女子小学生私って
ダメなのかな・・・
このように、解けなくて本人がより自信をなくしてしまうかもしれません。
ここで、今までやってきた問題集やテキストなどをもう一度振り返ってみましょう。
女子小学生ちょっと、
このテキストの問題を復習しよう！
一度「調子が良かった」「成績が良かった」経験があることは大事です。
過去の問題を振り返っている間に、子ども本人は、
女子小学生あの頃、
この問題をこうやっていたんだ・・・
このように振り返って、もう一度考え方を復習して、大事な考え方を再び習得するでしょう。
そうして、もう一度自信を持てるようにしましょう。
自信を持つことはとても大事です。
受験生の母親ちょっと調子が
良くないのかな。
受験生の母親すぐに元通りの
調子に戻るから。
このように、ただ「頑張れ」ではなく、
受験生の母親昔のテキスト復習したら、
出来るようになると思うよ。
受験生の母親昔のテキスト復習したら、
出来るようになると思うよ。
このように子どもを励ましてあげる姿勢が大事です。
過去に取り組んだ問題を、親が手書きでノートにまとめてあげるのも良いでしょう。
あるいは、塾の問題集やプリント等を、子どもに学んでもらうのも良いでしょう。
受験生の母親ママが、これまでの問題をピックアップして、
手書きでノートにまとめようか。
受験生の母親そして、そのノートで
復習してみたら。
このように「親が関わる」ことも、とても良いでしょう。
子どもなりに「親の努力」を感じるでしょう。
女子小学生お母さんも
一緒になってやってくれている・・・
女子小学生ちょっと
頑張ってみようかな・・・
このように「受験へ向けて『一緒に取り組んでいる』気持ち」をより強く持つでしょう。
ここで、あまりに志望校のレベルから下げ過ぎず、同レベル〜やや易くらいが良いです。
自信を持つためとはいえ、易しい問題に慣れないことが大事です。
レベルを下げすぎると、「算数の問題に対する感覚」がズレてしまう可能性があります。
志望校のレベルに応じて、「相応の問題を解けるようになること」の目標は変えないのが大事です。
理解の深化と有機的な理解へ：才能と試験の成績
図形問題ならば、基本的な相似形の考え方などを、もう一度復習してみましょう。
適度なレベルで「解ける」問題に、もう一度取り組んでみましょう。
そして、「解ける問題を完璧に理解することを目指す」ことをやってみましょう。
ここで「完璧」は「目指す」のであって、必ずしも「完璧でなくて良い」と考えましょう。
「完璧」というのは「目標」であって、実際到達するのは大変困難です。
「完璧目指すこと」によって、下記のような効果があります。
1.「解ける」という自信を取り戻す
2.過去に取り組んだ問題に再トライして、様々な解法が頭の中で有機的につながる
一度取り組んだことのある問題などを「完璧目指して理解」しようとすると、様々なことが結び付きます。
このように「頭脳の中で、様々な考え方が有機的に結びつく」ことが大事です。
すると、算数・数学は一気に「見えてくる」ようになります。
女子小学生どうやったら、
そのように「見えてくる」ようになるの？
女子小学生やっぱり、
才能なのかな・・・
中学受験の算数で、才能は大して関係ありません。
「算数の才能がある」方は「成績が良い」傾向はあるかもしれません。
一方で、その逆の「成績が良い」方が「算数の才能がある」とは限らないです。
いずれにしても、「才能と成績は全く関係ない」と「全否定」するのは難しいことです。
歴史の問題で「全否定は✖️」という話をしました（上記リンク）が、因果関係の判断は難しいです。
中学受験時に非常に優れた成績だった方の「その後」は、「ずっと優秀」ではないことが多いです。
「才能と成績は全く関係ない」と言い切るのは難しいです。
一方で、「才能と成績は大して関係ない」のが現実で、特に中学受験はその傾向が強いです。
成績が良くないことで、
女子小学生私は
才能ないかも・・・
このように子ども本人が、勝手に自信をなくさないように、
受験生の母親大丈夫だから、
ちょっとテキストやってみよう！
親が上手く子どもを激励することが大事です。
一度、スランプに陥ったとしても、様々な考え方を復習する「良いきっかけ」と考えてみましょう。
そのような前向きの姿勢での勉強が、「再起につながる」でしょう。
受験生ご本人が、女子御三家中の志望校に合格することを心より願っております。
次回は上記リンクです。
