算数の成績アップ勉強法〜基礎力を応用力に転換・算数の難問が解けるようになるコツ・「分からない」から「分かる」へ・暗記の学力と勉強時間・算数の学力と勉強時間〜｜中学受験・算数

前回は「算数の学力アップ学習法〜成績を上げるコツ・ポイント・「できない」から「できる」へ〜」の話でした。

理科・社会などの暗記の学力と勉強時間：算数の学力と勉強時間

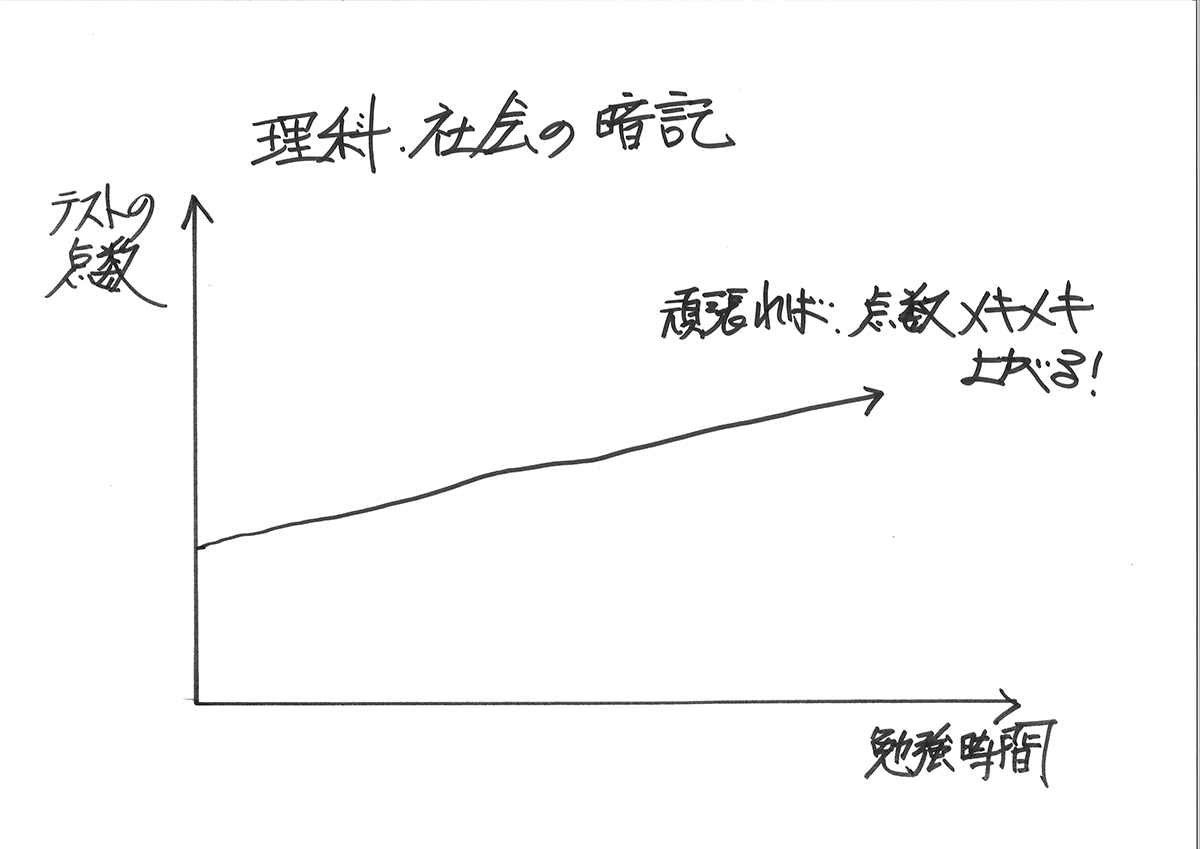
暗記問題等は、概ね「学んだ時間に応じて点数が上がる」傾向にあります。

横軸に勉強時間、縦軸にテストの点数をとってグラフを書いてみましょう。

暗記問題のテストの点数と勉強時間は、概ね上のグラフのようになります。

ここで注意が必要なのは、必ずしも「学力=テストの点数」ではないことです。

テストは制限時間がありますから、体調・調子にもよります。

テストの点数と学力は必ずしも同一ではありませんが、概ね「学力が上がれば、点数は上がる」です。

このように、理科や社会の暗記問題は、

「勉強を頑張れば成績アップ」の傾向があります。

ところが、算数は、なかなかそうはいかない面があります。

例えば、「つるかめ算」を習ったばかりの時を思い出してみましょう。

つるかめ算の考え方を習得したら、つるかめ算の典型問題は「すぐに解けるように」なります。

ところが、難関校〜最難関校の算数は、図形問題にしても文章問題にしても、

「応用問題が解けない」ことがあります。

そのため、算数は「学んだ時間に応じて、点数が上がる」にならないことがあります。

ある程度基礎を固めた後の応用問題は、なかなかすぐに解ける様になりません。

応用問題の算数は、

このように「成績が上がらない」と感じる状態が続くことがあります。

勉強すれば、「潜在的な学力は上がっている」はずです。

ところが、暗記問題と異なり、「なかなか具体的な試験の点数に結びつかない」のです。

算数の難問が解けるようになるコツ：「分からない」から「分かる」へ

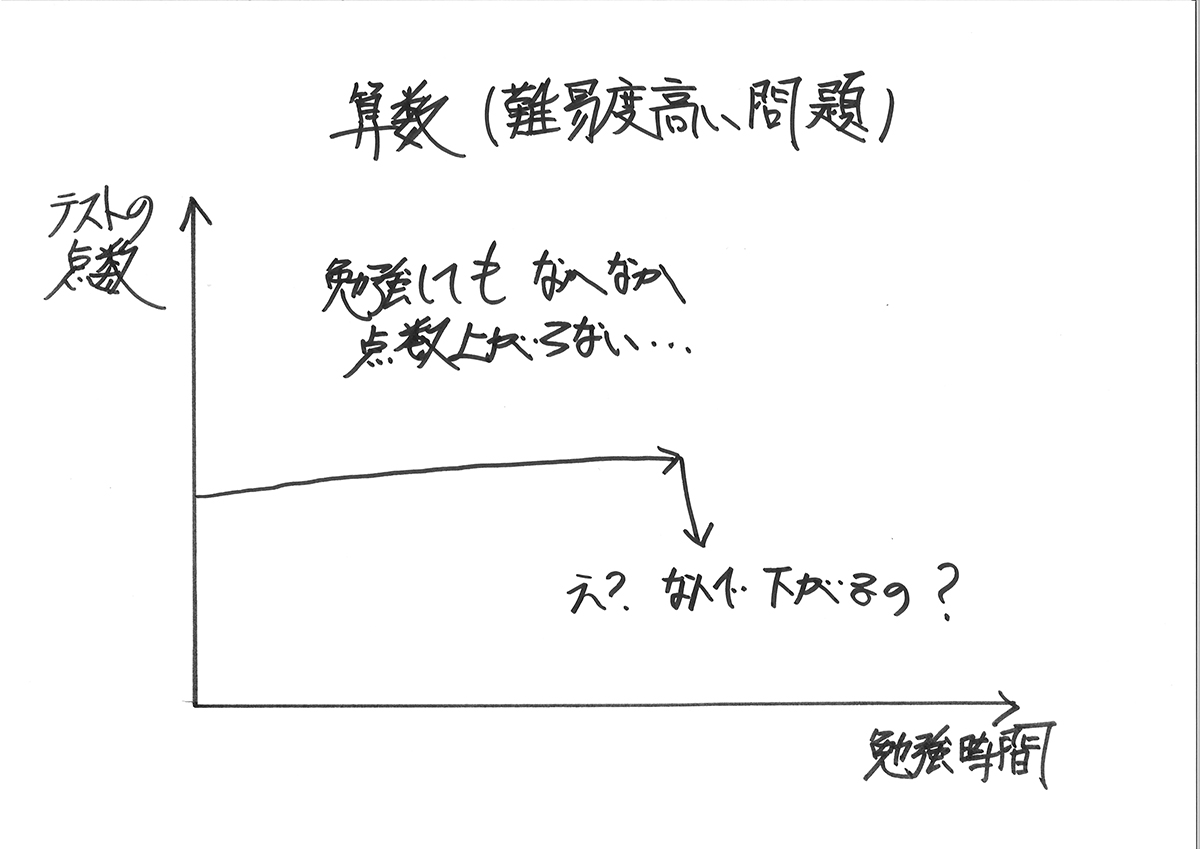
場合によっては、時として「点数（偏差値）が大きく下がってしまう」ことがあるのが算数です。。

こう「テンションが下がってしまう」可能性があります。

でも、ここでめげないようにしましょう。

これは、算数の科目の性質上「仕方のないこと」で「多くの方が経験すること」なのです。

算数の応用問題は、着実に・確実に「考え方」を身につけましょう。

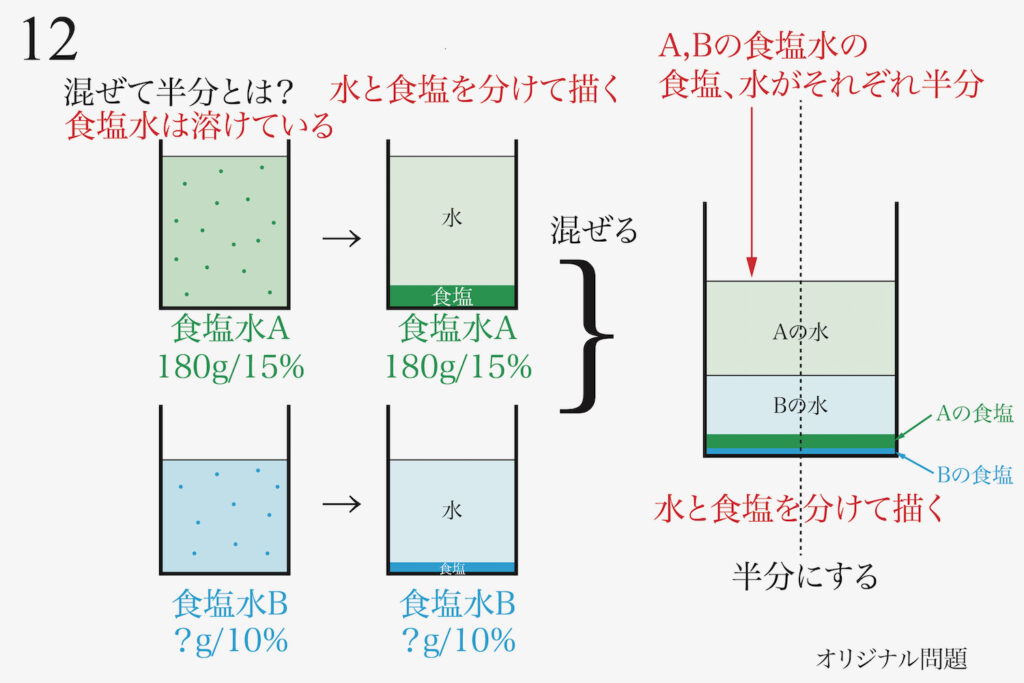
「考え方を習得する学び方」を継続してやってみましょう。

「きちんとした学び方」を続けてゆくと、しっかりと効果が出ます。（上記リンク）

上のてんびん算の問題では「混ぜて半分」の意味を図を描いて考えました。

このように「図に描く」や「図解する」姿勢で、応用問題・難問に取り組んでみましょう。

すぐには効果が現れなくても、2~3ヶ月後には

少しずつ学力アップを実感できるでしょう。

基礎的算数は「勉強すれば、確実に点数が上がる」のです。

応用問題の算数は「勉強してもなかなか上がらない」のです。

時には、意地悪のように点数が下がったりします。

こういう状況になると、誰しもテンションが下がってしまいます。

「算数のセンス」がある、ないを考えてしまうこともあります。

中学受験の算数の点数と算数のセンスは、大して関係がありません。

こういう「ちょっと成績が良くない」時も、

このように考えて、ポジティブに勉強を続けましょう。

算数の成績アップ勉強法：基礎力を応用力に転換

算数は、基礎力が最も大事な科目です。

建物も「基礎が最も大事」で、基礎の上の柱・梁などを支えるのは基礎です。

センスは多少の影響があるかもしれませんが、きちんと努力することで一定のレベルには到達できます。

「基礎を学んだのに学力が思うように上がらない」からといって、

このように感じる時こそ、「基礎に戻る」のがお勧めです。

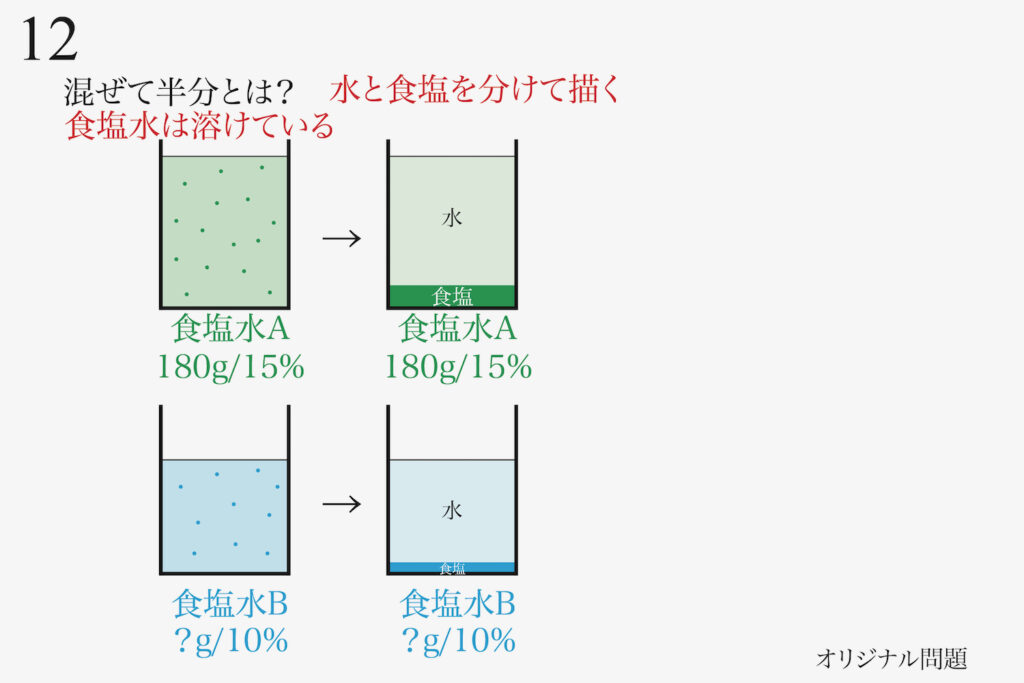
先ほどの「食塩水を混ぜて半分」を考えるのは、少し難しいことかも知れません。

少し難しいかも知れませんが、「食塩水は食塩が水に溶けている」という基本を図解して考えました。

基礎をきちんと踏み固めて、しっかりと土台を作りましょう。

その上で、応用問題は色々と試行錯誤しながらやってみましょう。

「手を動かして、しっかりと学ぶ」ことが大事です。

勉強すると、学力はきちんと上がっているはずです。

ただ、「定められた時間内での試験での点数」がなかなか上がらないだけであることが多いです。

模試や試験の後に解答を読んで、

このように、悔しくなることがよくあります。

「本当は分かっていた」のに「制限時間内に思い付かなかった」のです。

少し我慢して、手を動かして一生懸命学んでみましょう。

ノートは「きれいな方が良い」ですが「きれいに書く・描く必要はない」です。

特に、算数は「きれい」を目指さずに、どんどん書いて・描いてみましょう。

するとある時、色々な考え方が分かる時が来て、

算数の学力・成績がアップする時期に至るでしょう。

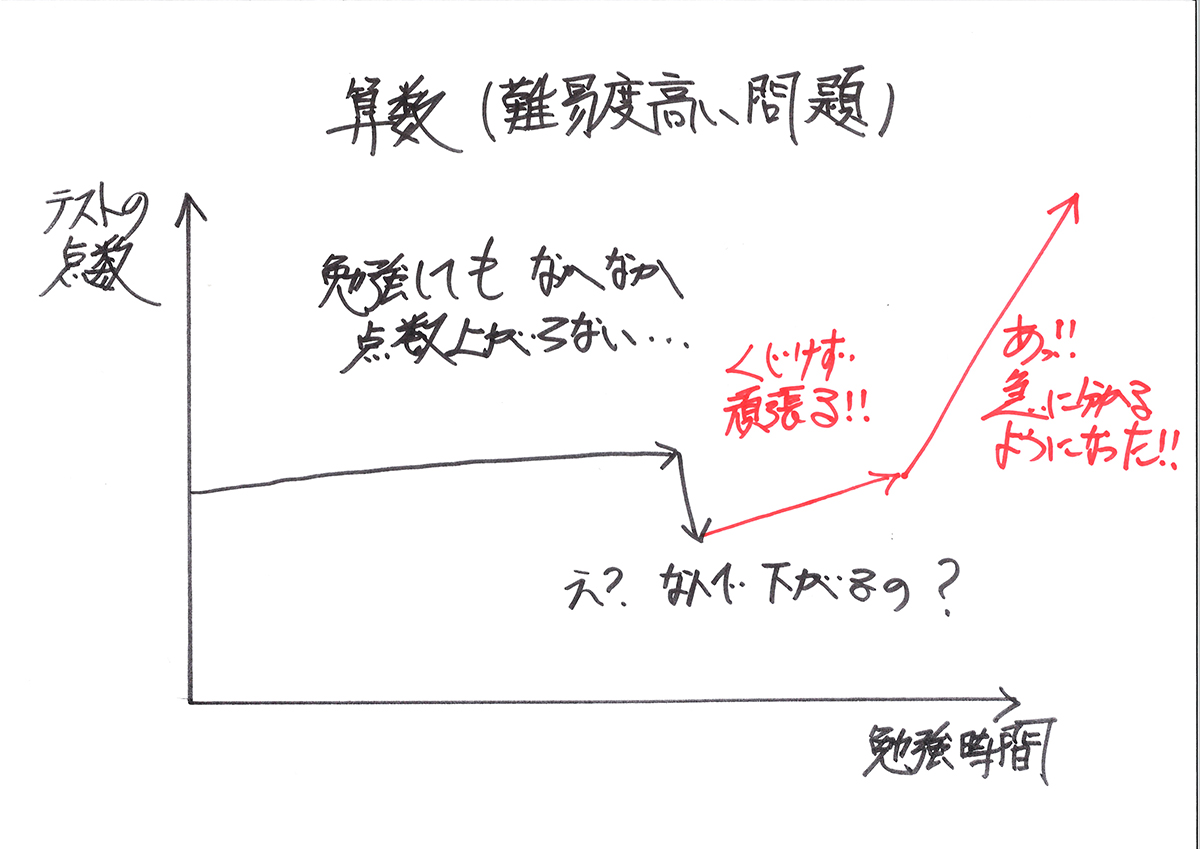
1,2ヶ月では効果が見受けられないかも知れません。

「自分でしっかり考える」スタンスを身につければ、ある地点で学力が急成長します。

上のグラフでは急な直線で描きました。

放物線（二次関数）のように、急激に学力が上がる場合もあります。

頭の中で「様々な点（解法）と点（考え方）が結びついて」一気に「分かるようになる」時が来ます。

「いつ・どう上昇するか」は「人それぞれ」です。

目の前の点数アップを追いかけるよりも、確実に基礎を固めてみましょう。

そして、応用問題は「一題一題きちんと理解」をやってみましょう。

このような、「着実な学び」を続ければ、少しずつ手応えができて、

このように「理解力が上がる」時が来るでしょう。

「そういう時」が来る時期は、一人一人異なります。

しっかりと学習すれば、

このような時期が来るでしょう。

そういう時を楽しみにして、算数を楽しく勉強してみましょう。

次回は下記リンクです。