前回は「二つの正方形と相似形が得意になるコツ・ポイント〜学力を高める姿勢・テクニックやパターンと「考え方の骨格」・しっかり理解して一題から多くを学ぶ・応用力構築・相似形を探す・「分かっていること」を描いて視覚化・問題 13(1)解法〜」の話でした。
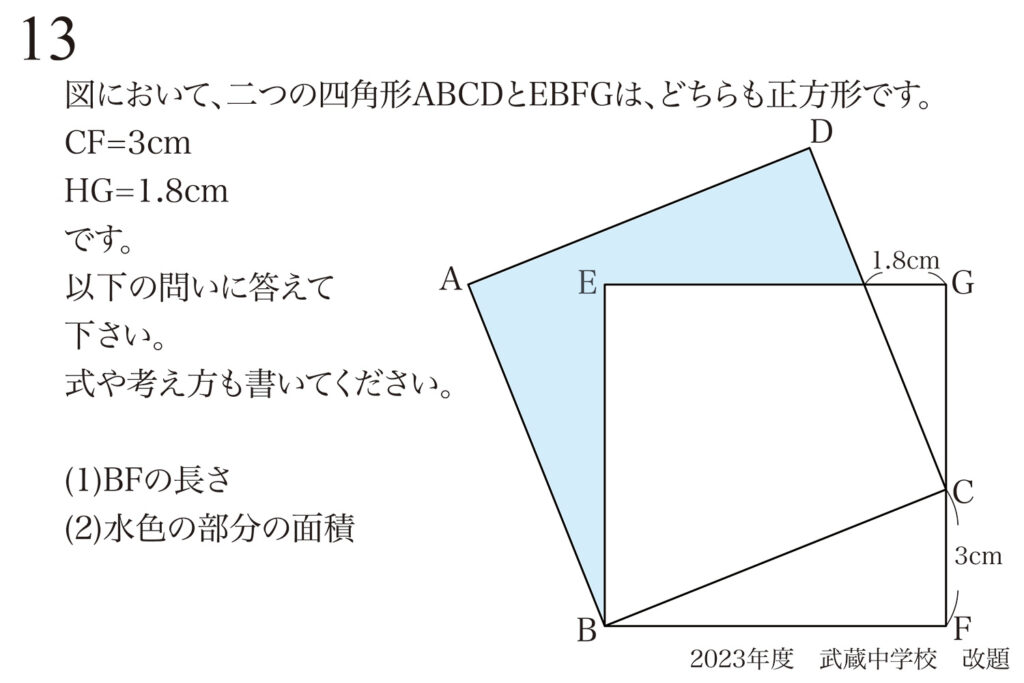
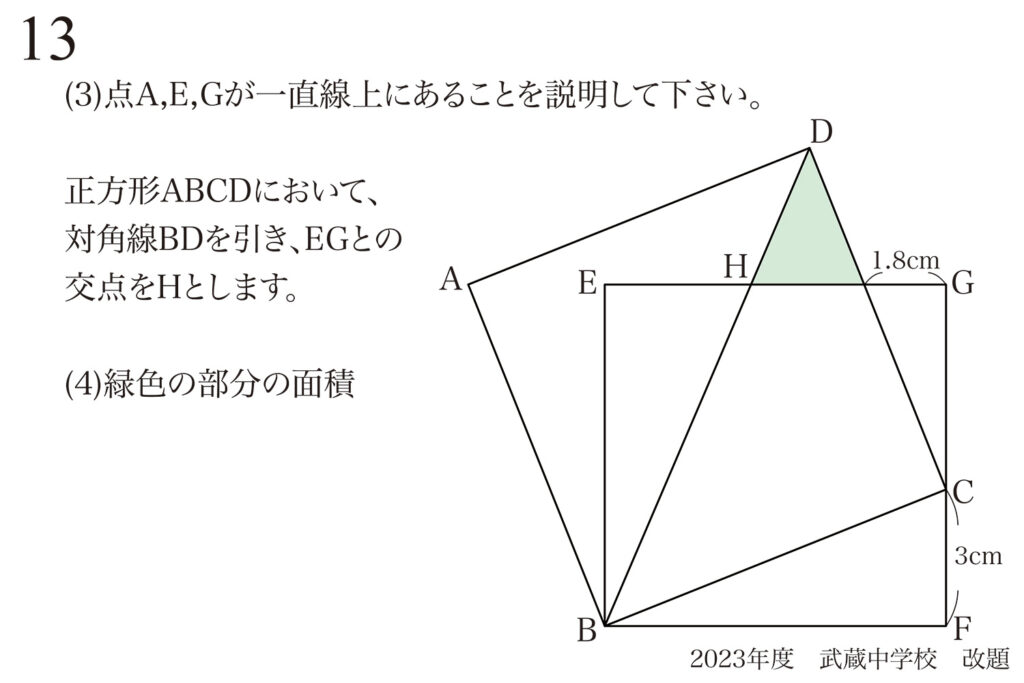
問題 13
斜めの正方形と相似形攻略のポイント
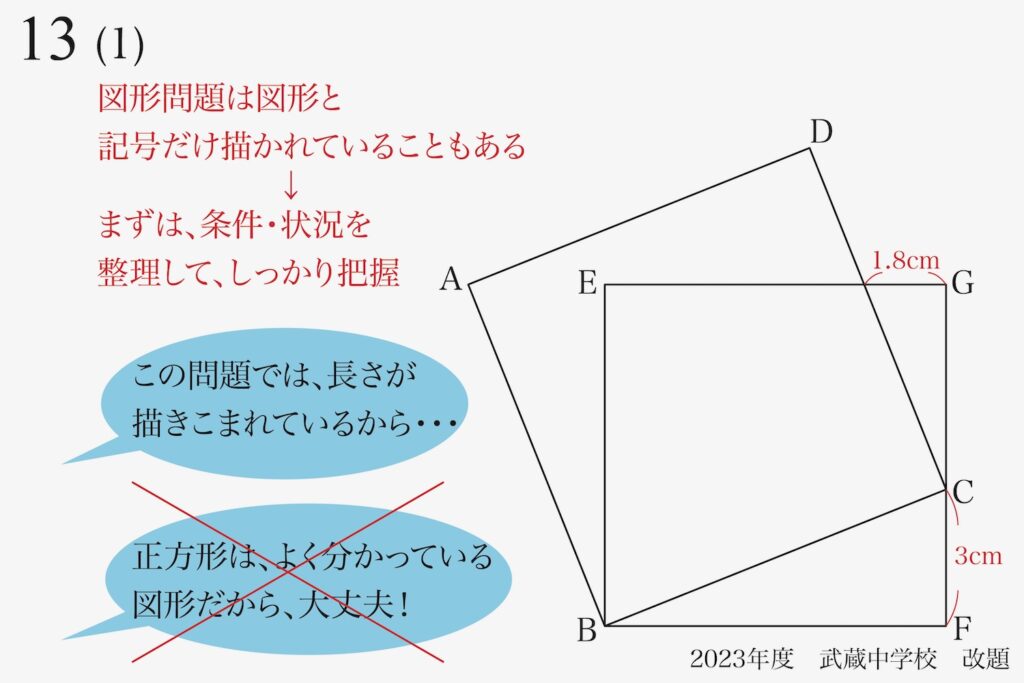
二つの正方形が登場する問題13では、「よく分かっている正方形をしっかり描いて理解」が大事です。
・全ての辺が同じ長さ
・全ての角が同じで直角
幼稚園〜小学校低学年で、方眼紙でたくさんの工作をした方が多いと思います。

方眼紙のマスは全て正方形です。
大抵は「1cm(10mm)角の正方形」で、工作するときに「切るのが簡単」です。
それだけに、「みんなが馴染み深い」正方形という図形。
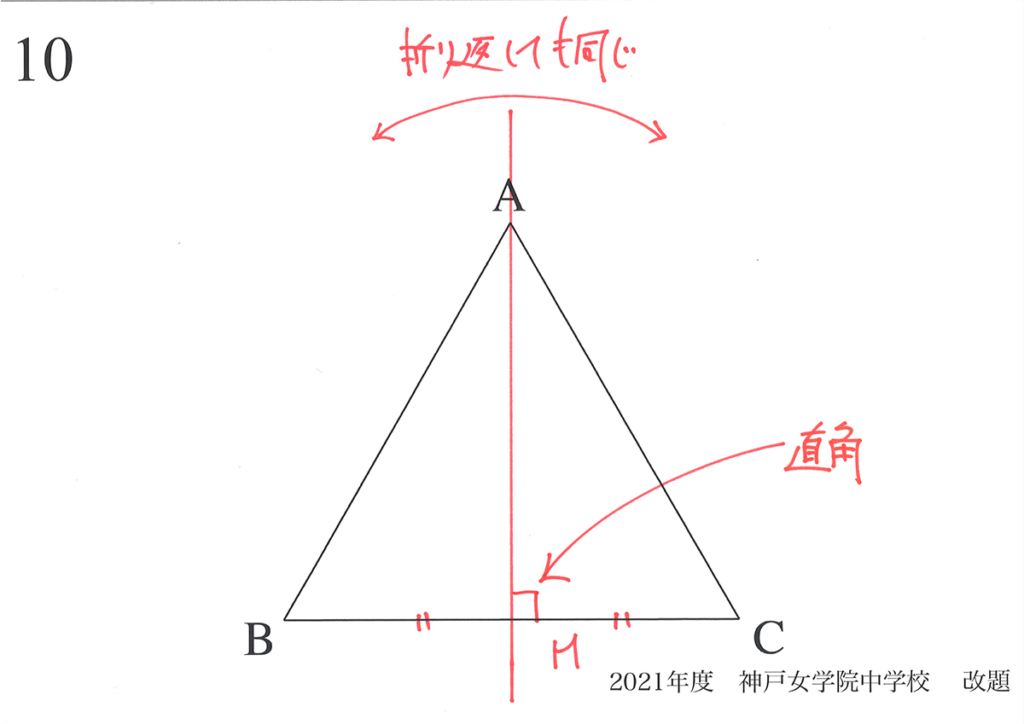
正三角形も基本的図形ですが、「日常生活で正三角形に出会う」ことはほとんどありません。
正三角形と動く点を考えるコツを、上記リンクでご紹介しています。
日常生活の周りを見渡してみると、長方形がたくさんあります。
「厳密な正方形」は少なくても、「特殊な長方形」である正方形も馴染み深い図形です。
・長方形の中で「辺の長さが全て等しい」特殊な図形が正方形
・長方形と正方形は同じグループで友達
とても分かりやすい正方形ですが、実は「最も奥が深い図形」とも言えます。
そして、「長方形と正方形は同じグループで友達」という認識を持ちましょう。
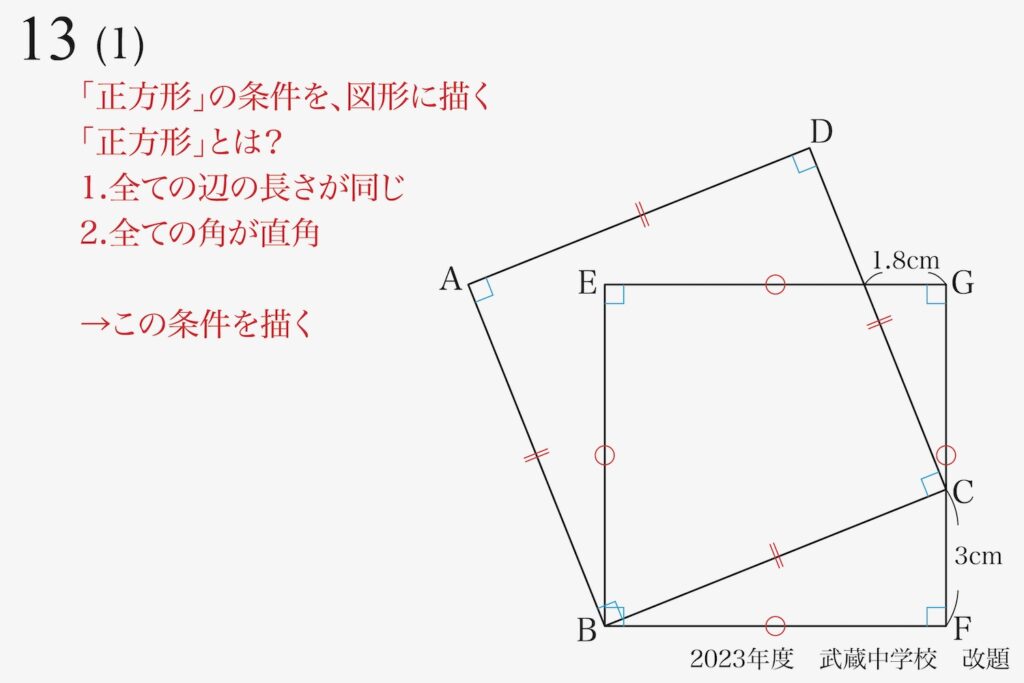
問題の状況を全て図形に描きこみました。
 男子小学生
男子小学生確かに、こうして
描きこんだ方が分かる気がする・・・



「全部わかっていること」なのに、
描いた方が分かるね!
「斜めの正方形」が登場すると、難しく感じられます。
「斜め」というのは日常生活であまり馴染みがないので、「ちょっと変な感じ」があるからです。
「ちょっと変」な斜めの図形ですが、正方形には変わりありません。
・斜めの図形も性質は同じ
・具体的な性質を描きこんで、図形の特徴を探す
慣れるまでは「難しく感じられる」斜めの図形ですが、「斜めと水平(垂直)の図形」には共通点があります。
(1)は、難関校〜最難関校志望の方にとっては、それほど難しい問題ではありません。



この問題は
出来たよ!
すぐ出来る方もいれば、



ちょっと、
よく分からない・・・
なかなかうまく行かない方もいらっしゃると思います。
後者の方向けに、少し丁寧に話を進めてみましょう。
様々な分野の中でも、中学受験算数の平面図形は「基本をしっかり」すれば全部解けるようになります。
高校以降の平面図形も「基本をしっかり」ですが、様々な法則や性質が登場して難しくなります。
「法則と性質が限られている」のに「難問が多い」中学受験算数の平面図形。
様々な図形に対して、解法もまた様々です。
「解法を一つ一つ習得」するのも一つの手段です。
そして、「共通する基本的考え方」を身につけることがさらに重要です。



ちゃんと
出来たよ!
出来た方も、確認のためにぜひご覧ください。
「なんとしても相似形を見つける!」姿勢:相似形とは何かと直角の性質
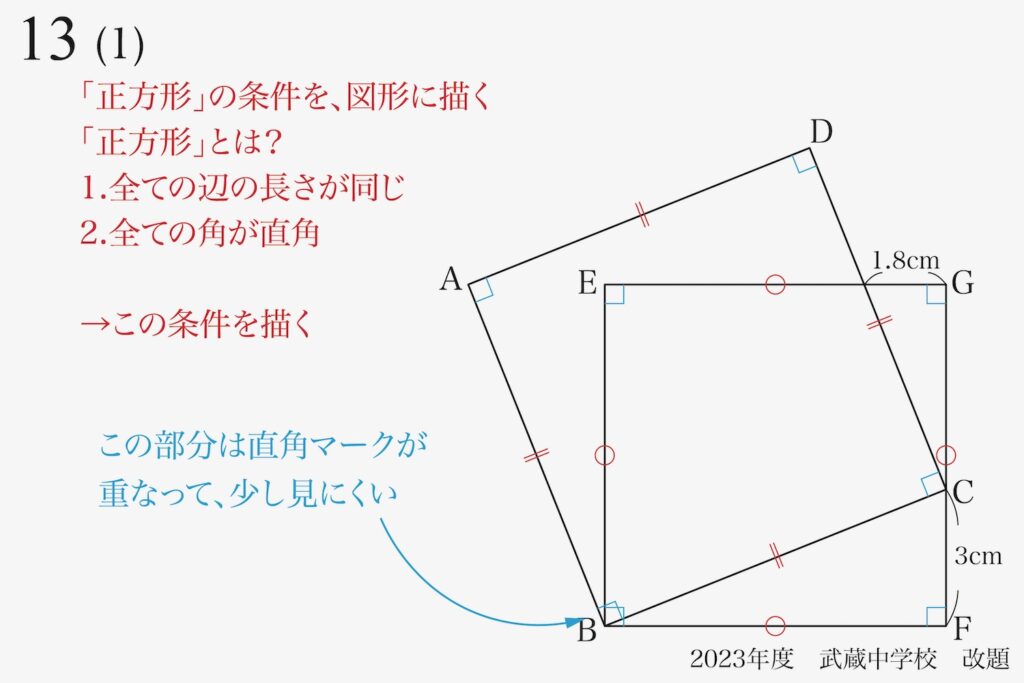

まずは「描いて状況をしっかり理解」しましょう。
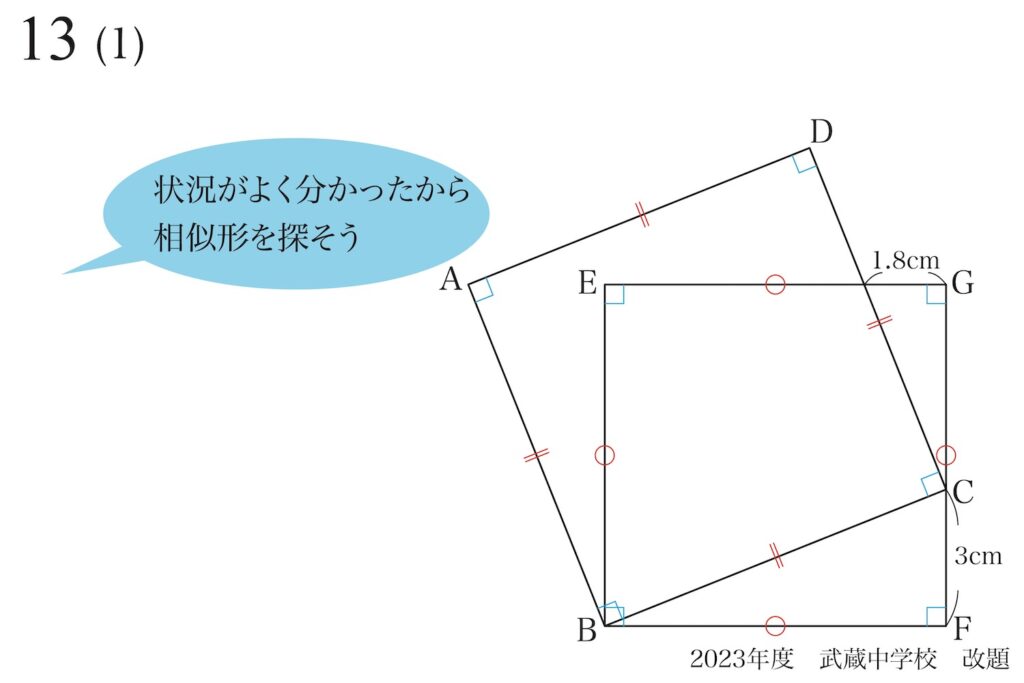

「まずは相似形」の図形問題。
しっかりと状況を理解したら、相似形を探してみましょう。
この「相似形を探す過程」で、「適切な補助線」が見つかることがあります。
「なんとしても合格する!」という気持ち同様「なんとしても相似形を見つける!」と考えましょう。
・ある形AとBが「相似」
→片方の図形を拡大・縮小すれば、もう一方の図形となる
・相似の条件
←→対応する角度が同一
←→対応する辺の比が同一
「相似形」というと算数(数学)の専門用語となりますが、難しくはありません。
「相似形とその条件」を、もう一度復習しておきましょう。
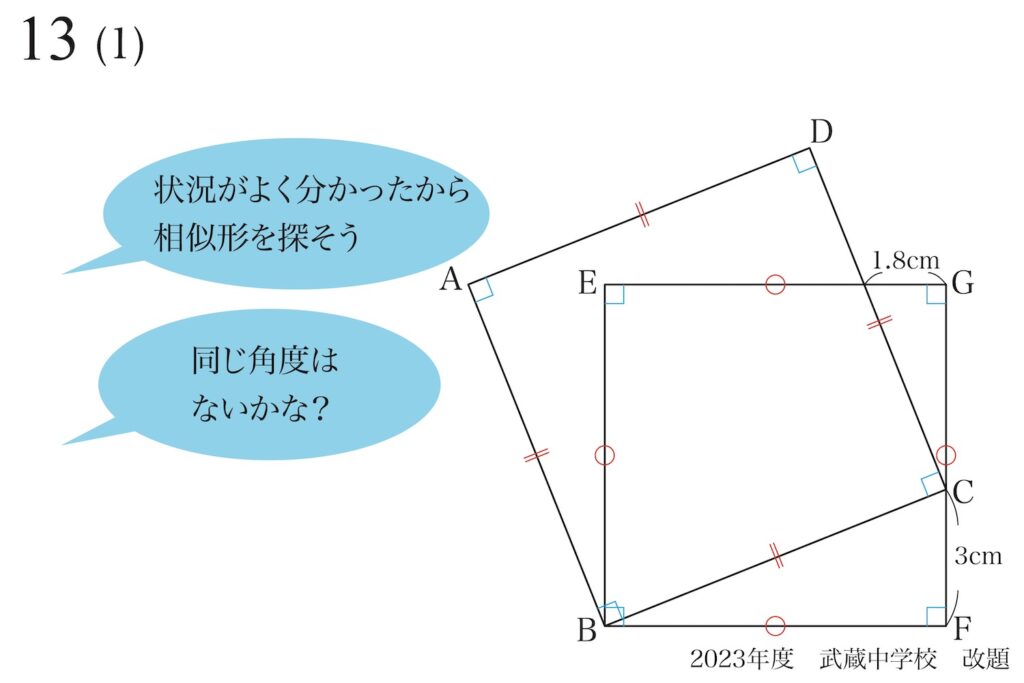

「対応する辺の比が同一」の条件を見つけるのは、なかなか難しいです。
対して「対応する角度が同一」は、角度を一つ一つ検討してゆけば出来そうです。
「同じ角度」を探しましょう。
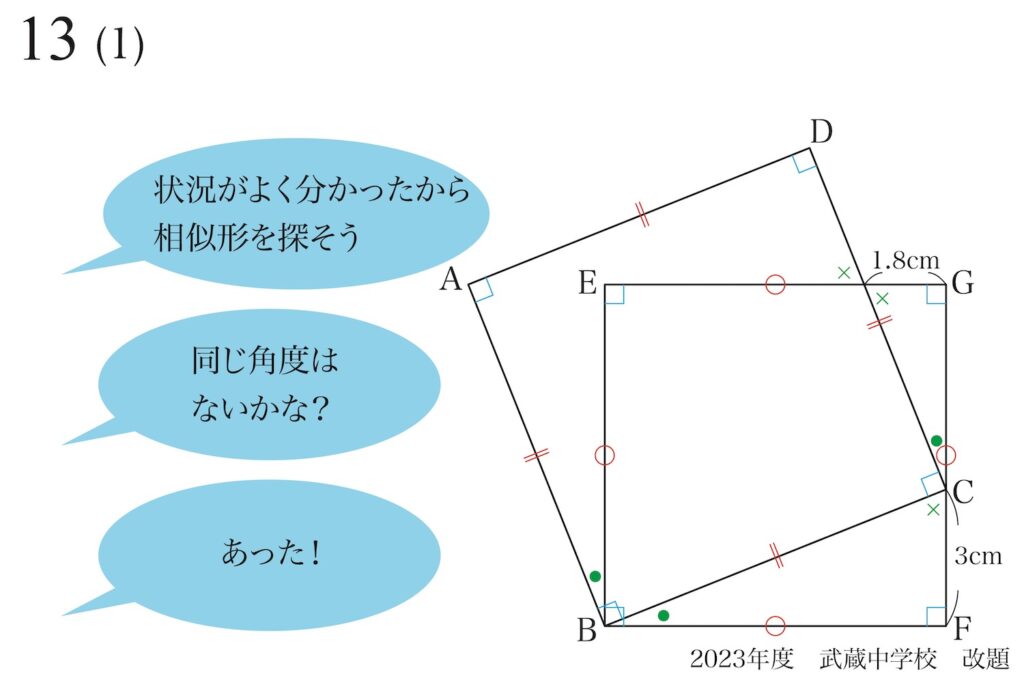

直角がたくさんあるので、たくさんの「同じ角度」が見つかりました。
「180度から直角(90°)を引くと直角(90°)(180-90=90)」です。
「直角は同一角度が見つけやすい」と考えましょう。
・180度から直角を引くと直角:180-90=90
・直角は同一角度が見つけやすい→相似形が見つかりやすい
相似形を見つけたら辺の比:直角三角形の辺の長さ
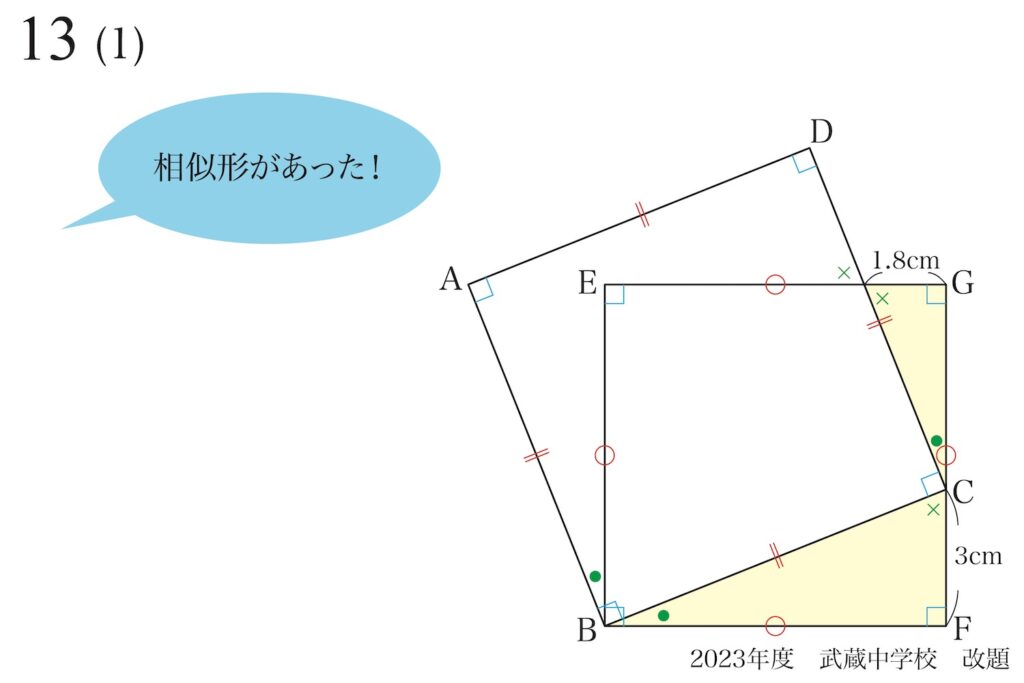

「同一の角度」が沢山見つかり、相似形が見つかります。
・問題の条件を全て描きこむ:同じ長さ・同じ角度など
・図形の性質などを描く過程で、条件を頭で整理するので解きやすくなる
まずは「相似形を一組見つける」を心がけましょう。
一組以上見つかるかもしれませんが、「まず一つ(一組)」という気持ちが大事です。



確かに一つ見つかると、
調子が良くなって、解けやすくなる・・・



まずは「最初のキッカケが大事」
なんだね!
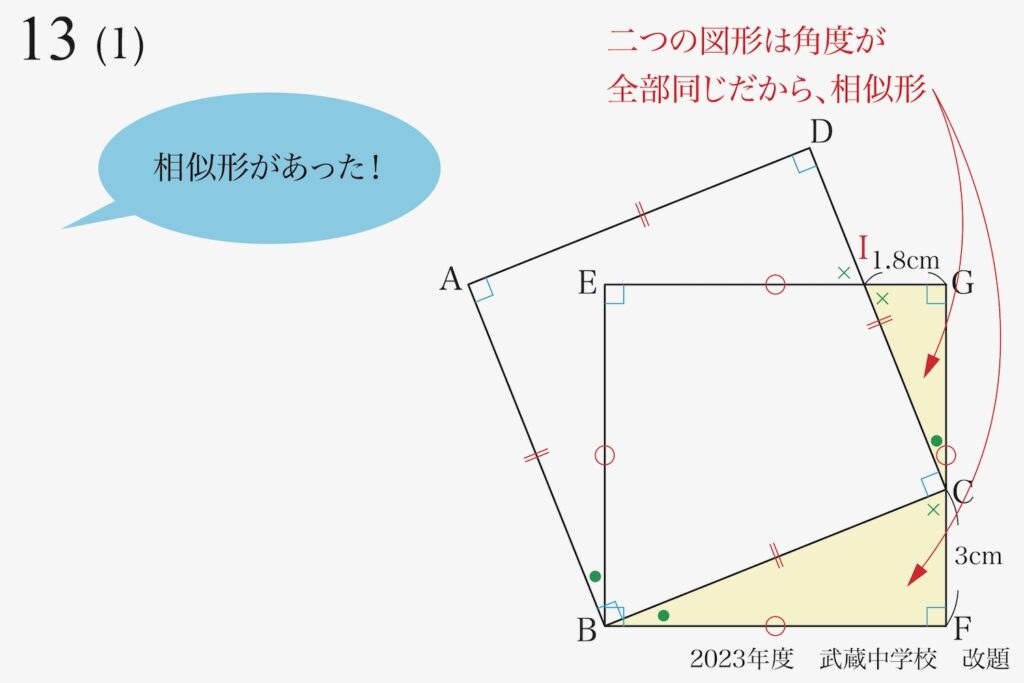

黄色の三角形同士が「対応する角の角度が同一」なので、相似形となります。
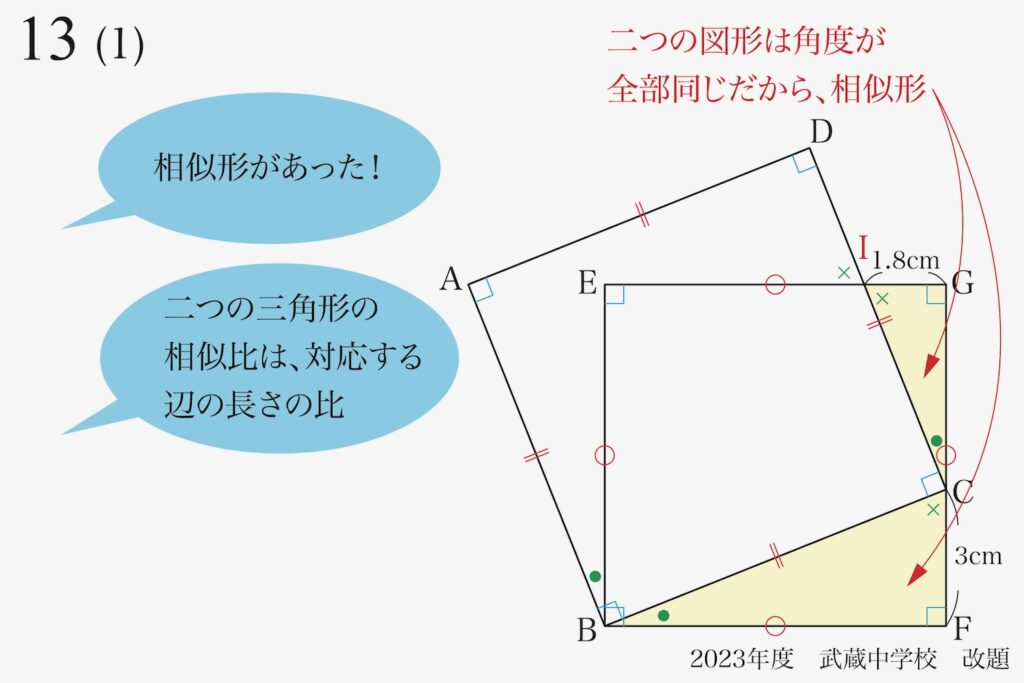

相似形が見つかれば、図形問題は一気に見通しが良くなります。
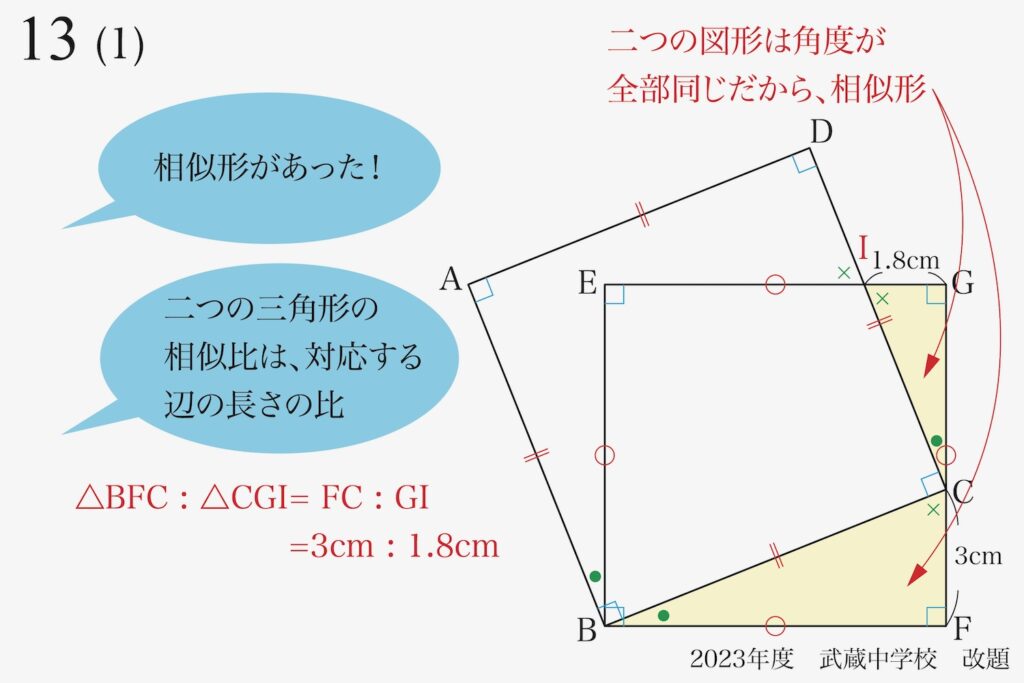

二つの黄色の三角形の「対応する辺の長さ」が分かっているのがポイントです。
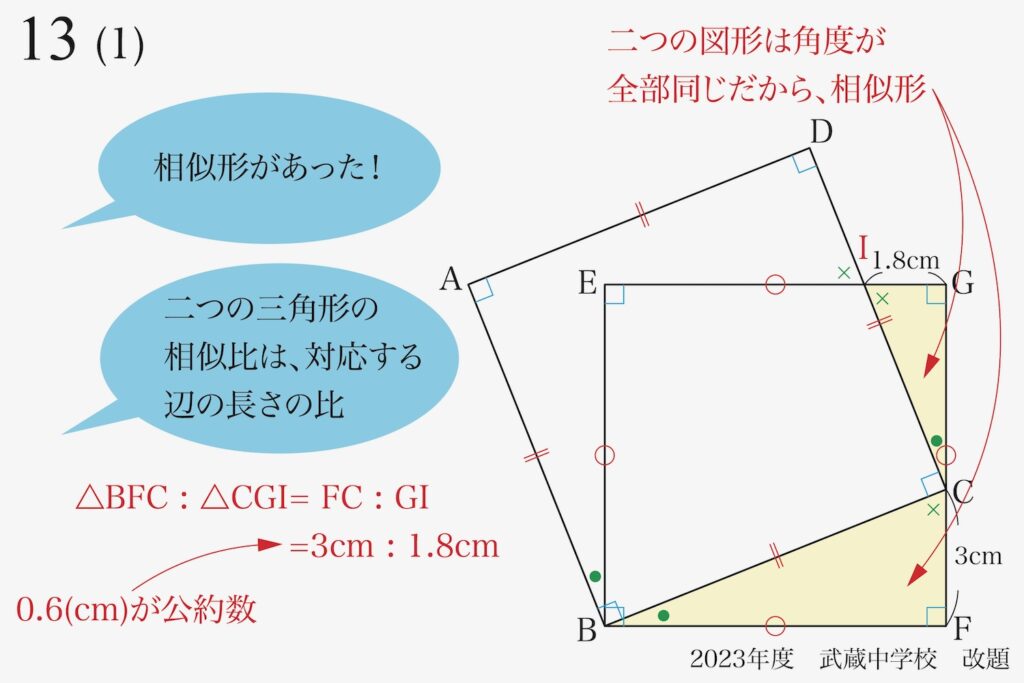

これで、双方の黄色の三角形の「対応する辺の長さの比」=3.0 : 1.8と分かりました。
「相似比」の元となる「辺の長さの比」には公約数(少数含む)があることが多いです。
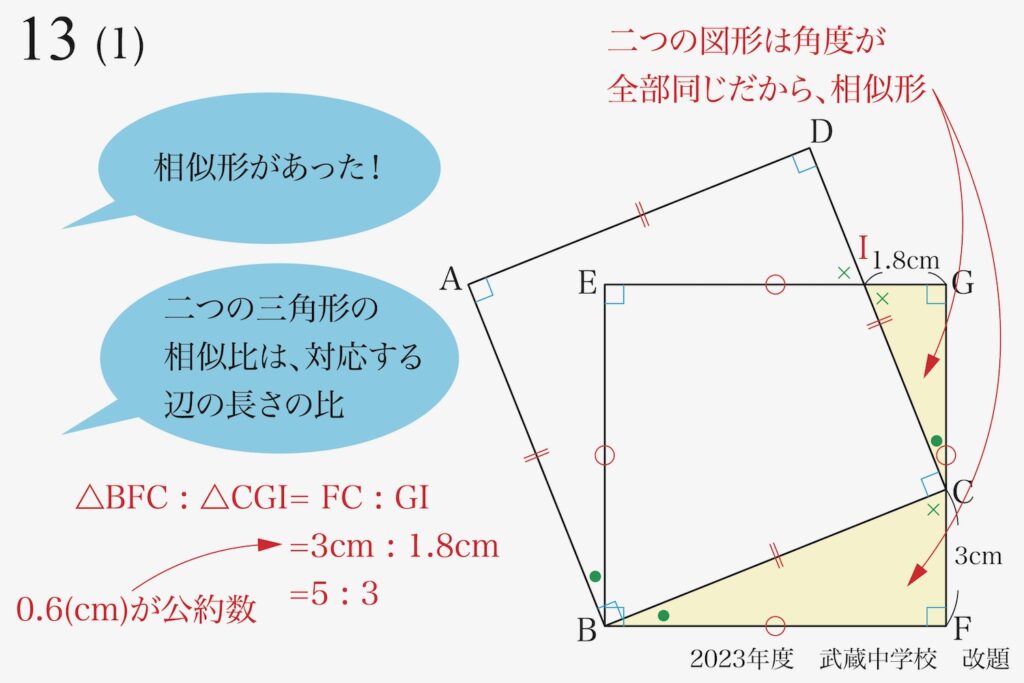

黄色の三角形同士の「相似比=5 : 3」と分かりました。
これで、問題の図形のポイントが分かりました。
一つ相似形を見つけたら、



これで、一つ
ポイントをつかんだ!



問題を解く山を
一つ乗り越えた!
このように考えると良いでしょう。
そういう「前向きな気持ち・姿勢」を持つことも大事です。
出来なかった方も、ここからもう一度図形を見直して、解いてみましょう。
次回は下記リンクで、(1)を求めます。




