斜めの正方形と相似形と長さのポイント〜「一組の相似形」発見・問題の条件を振り返る姿勢・直角三角形の辺の長さ・描いた条件から発見・条件を組み合わせて立式・問題 13(1)解法〜｜武蔵中2023年算数4・過去問・中学受験

前回は「斜めの正方形と相似形攻略のポイント〜「なんとしても相似形を見つける！」姿勢・相似形とは何か・直角の性質・相似形を見つけたら辺の比・直角三角形の辺の長さ・問題 13(1)解法〜」の話でした。

問題 13

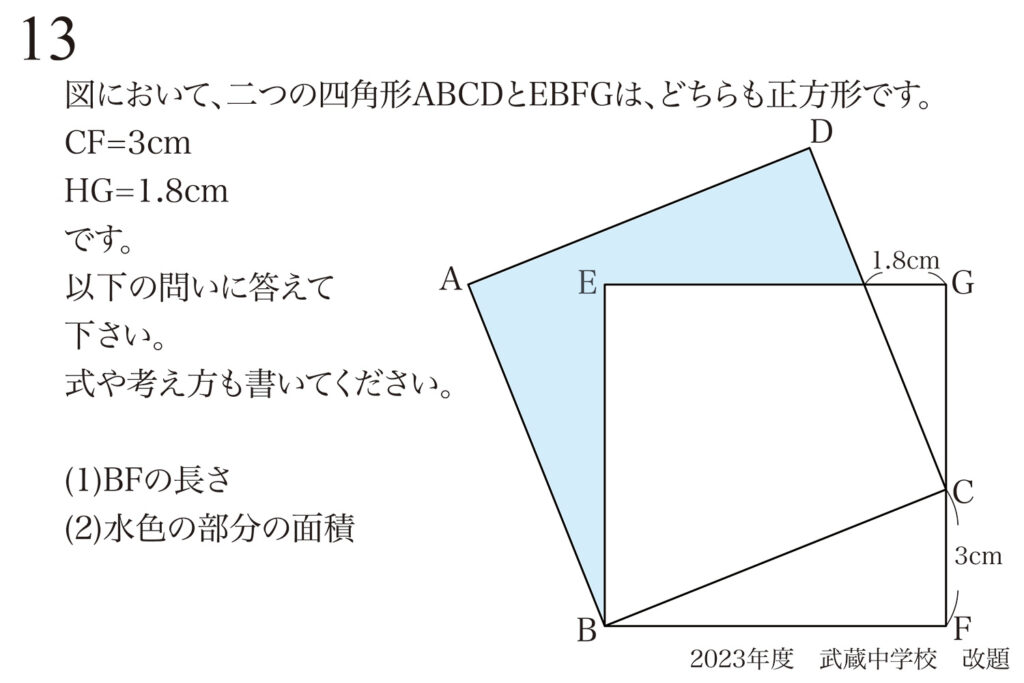
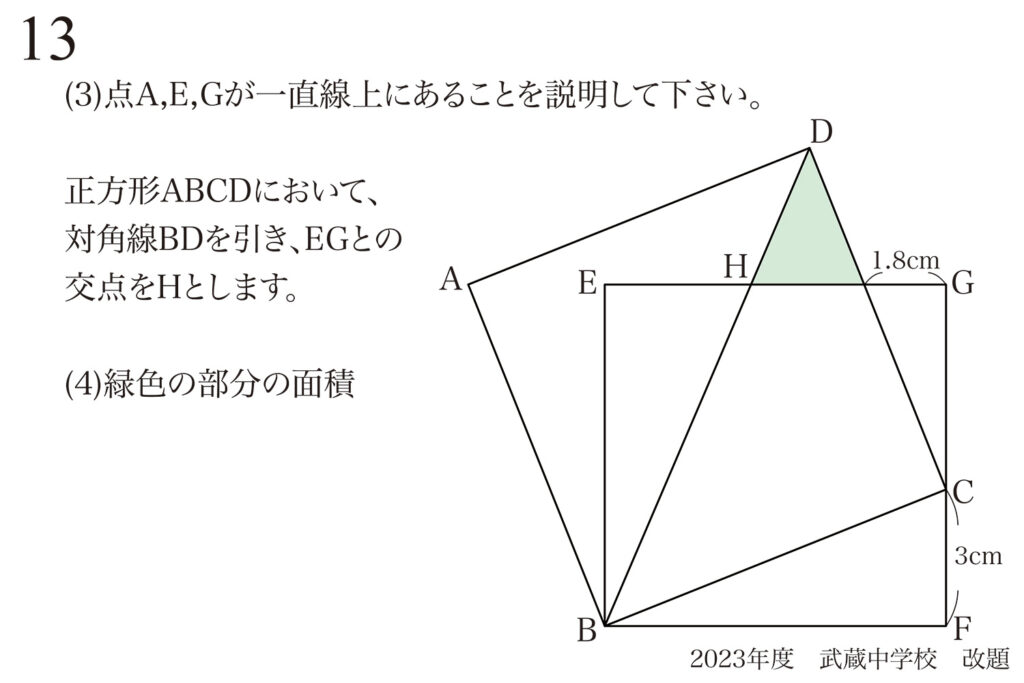
「一組の相似形」発見：問題の条件を振り返る姿勢

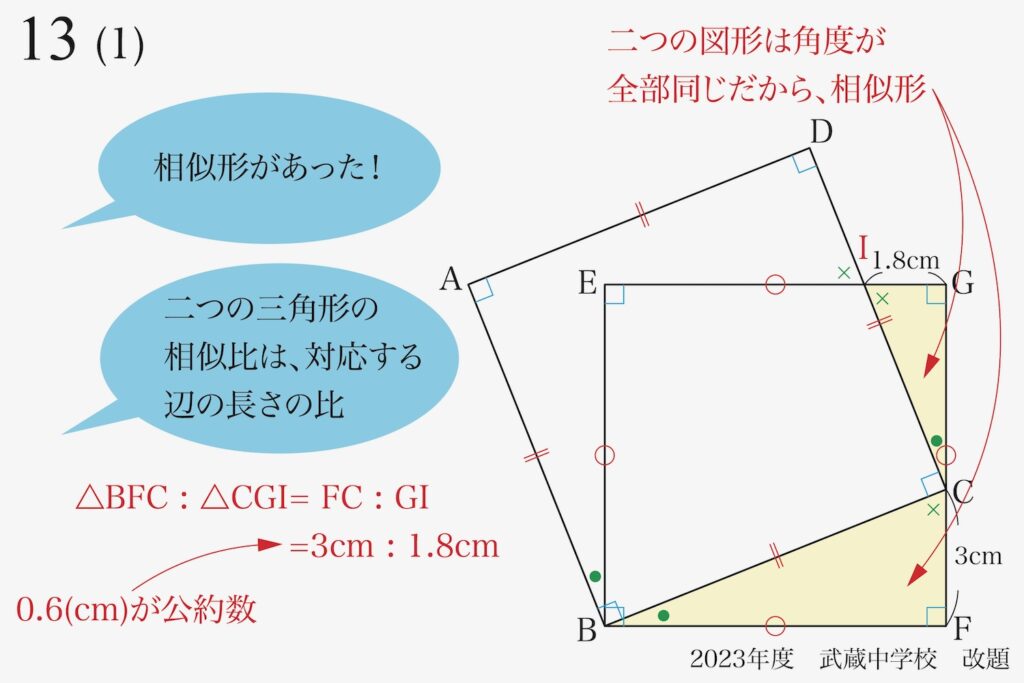
相似形が一組見つかり、さらに相似比が分かりました。

相似比が分かる相似形を一組見つけたら、

ポジティブに考えるようにしましょう。

「見つけた相似比の分かる相似形」が、「必ず解法に至るか」は、問題によります。

「相似形がポイントであることが多い」図形問題。

一組の「相似比の分かる相似形」が決定的であることが多いです。

一つ・一組の条件が分かることは、算数・数学では「とても大きな前進」であると考えましょう。

「二組以上の相似比が分かる相似形がある」場合は、図形の構成が分かりやすい場合です。

パッとみて分かりにくいような図形問題は、まずは「相似比の分かる一組の相似形」発見を目指しましょう。

直角三角形の辺の長さ

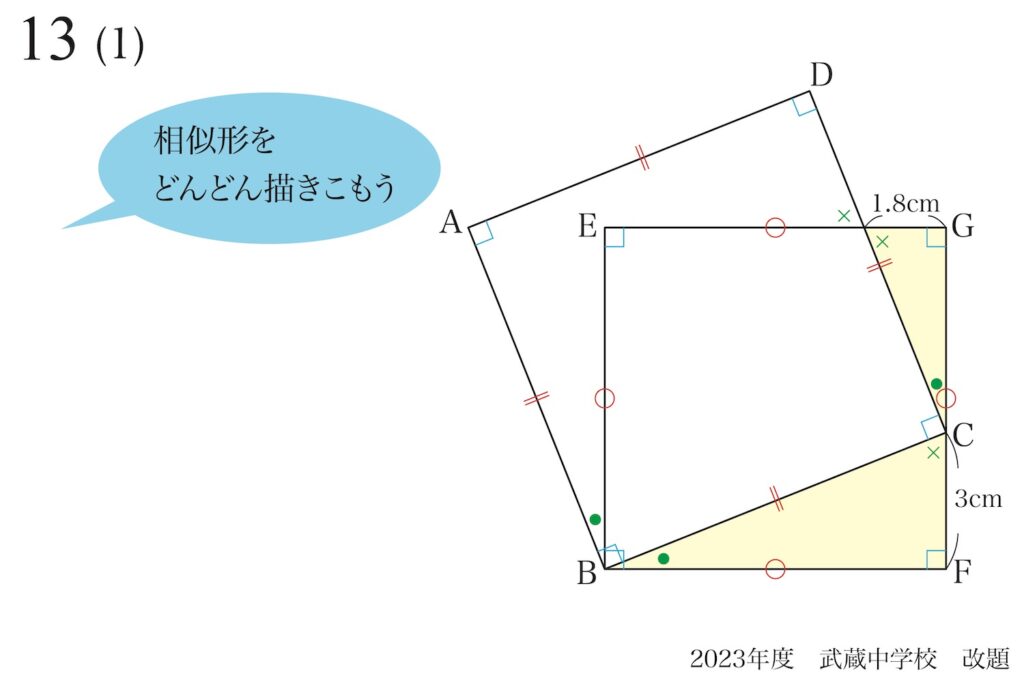
「一組の相似形」を見つけたら、手をどんどん動かすことが大事です。

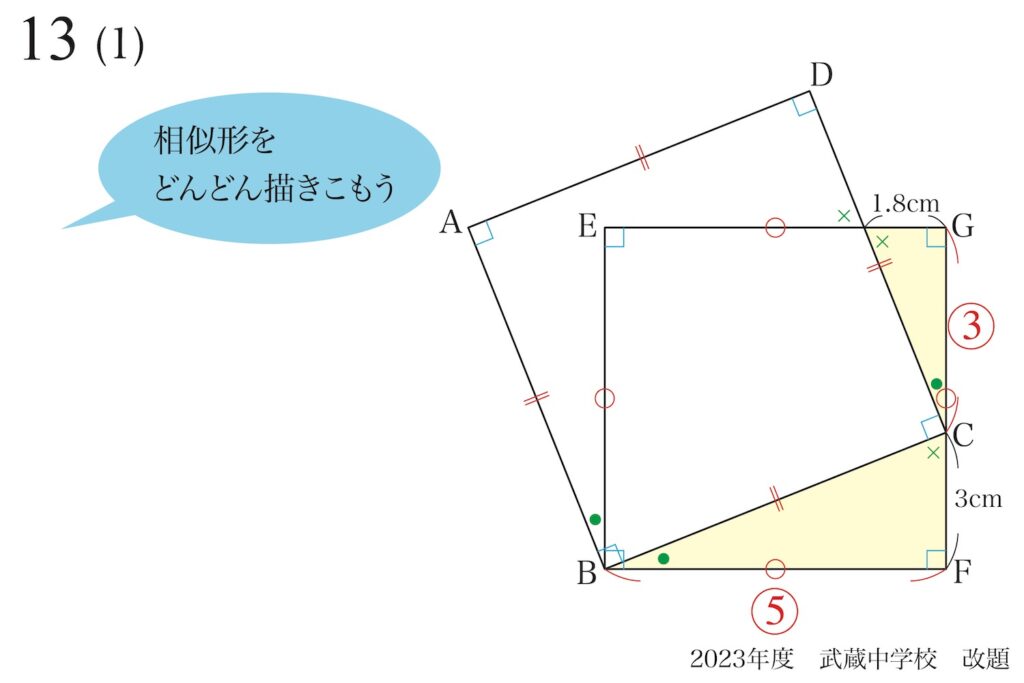
「一組の相似形」を見つけたら、相似比を描きこみましょう。

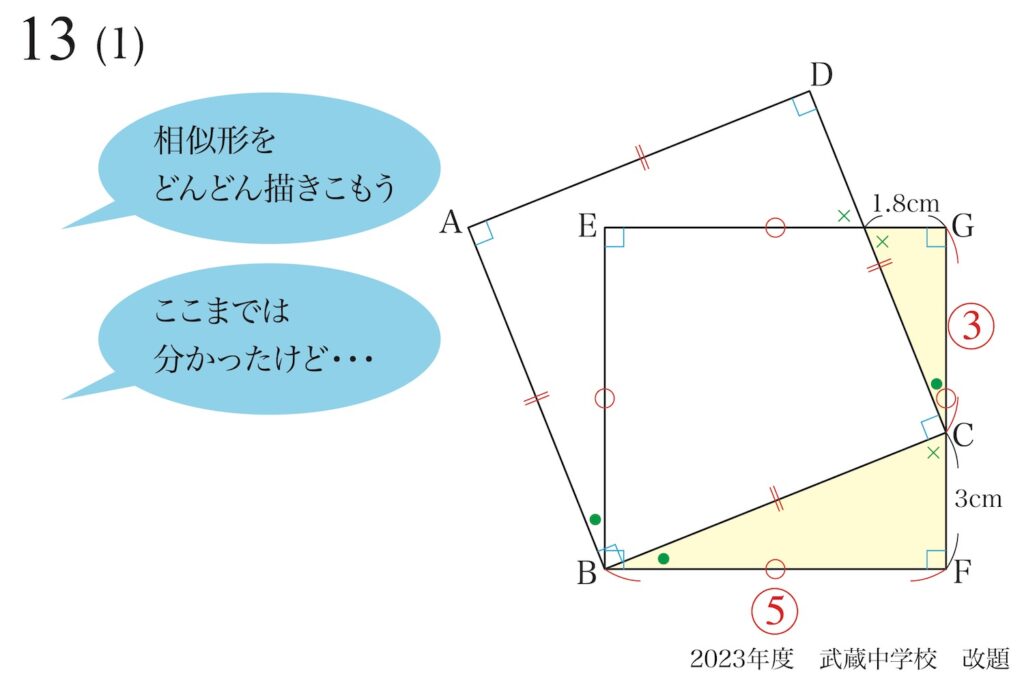
黄色の二つの三角形の斜辺も同じ相似比（=5 : 3）になります。

斜辺は長さが分かりにくいことが多いので、直角三角形ではまずは直角を挟む二辺がポイントです。

ここまで手を動かして、少し悩むことがあります。

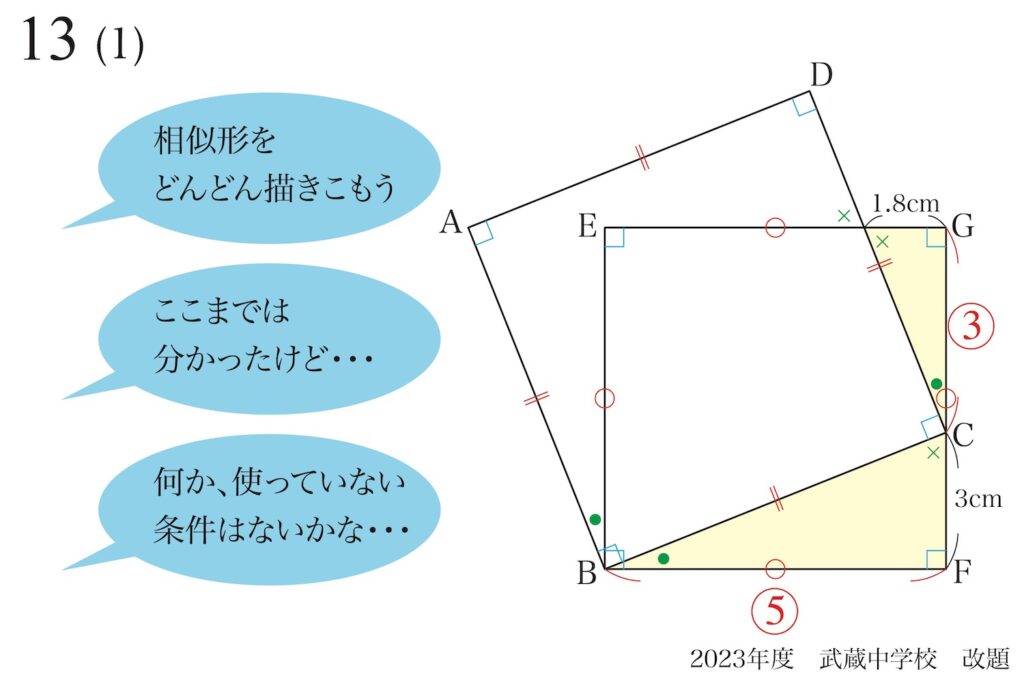
手が止まってしまった時は、

と探してみましょう。

ここで、図形をもう一度じっと眺めてみましょう。

こういう時は、多くの場合に「同じ長さの辺」や「長さの比が分かる辺」などがあります。

描いた条件から発見：条件を組み合わせて立式

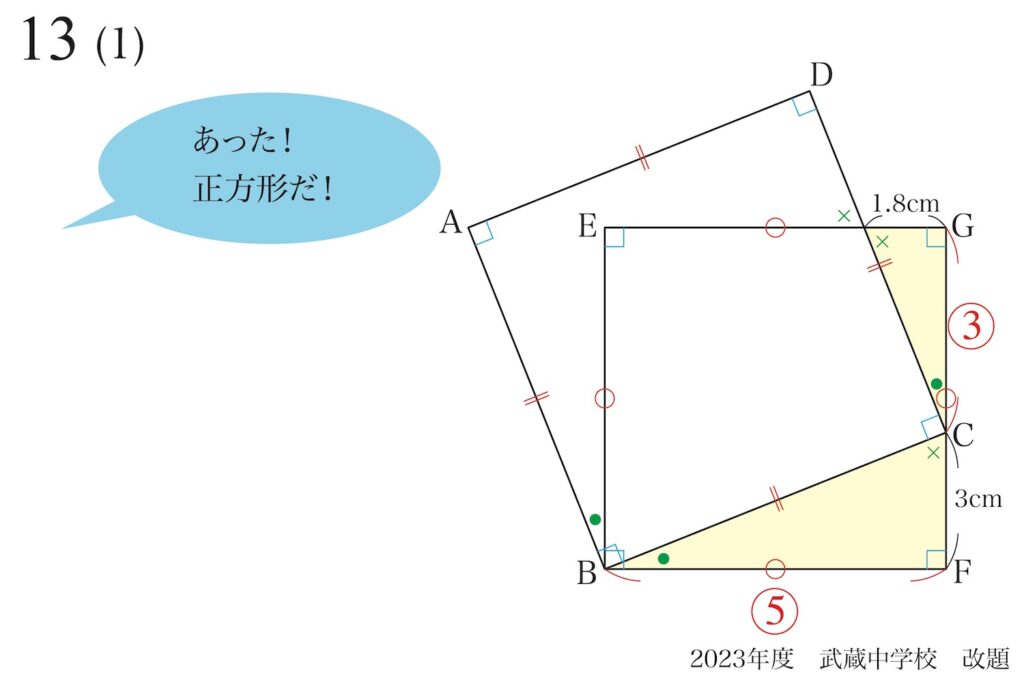
ここで、最初に「状況を整理」していたことが役立ちます。

「正方形の条件」です。

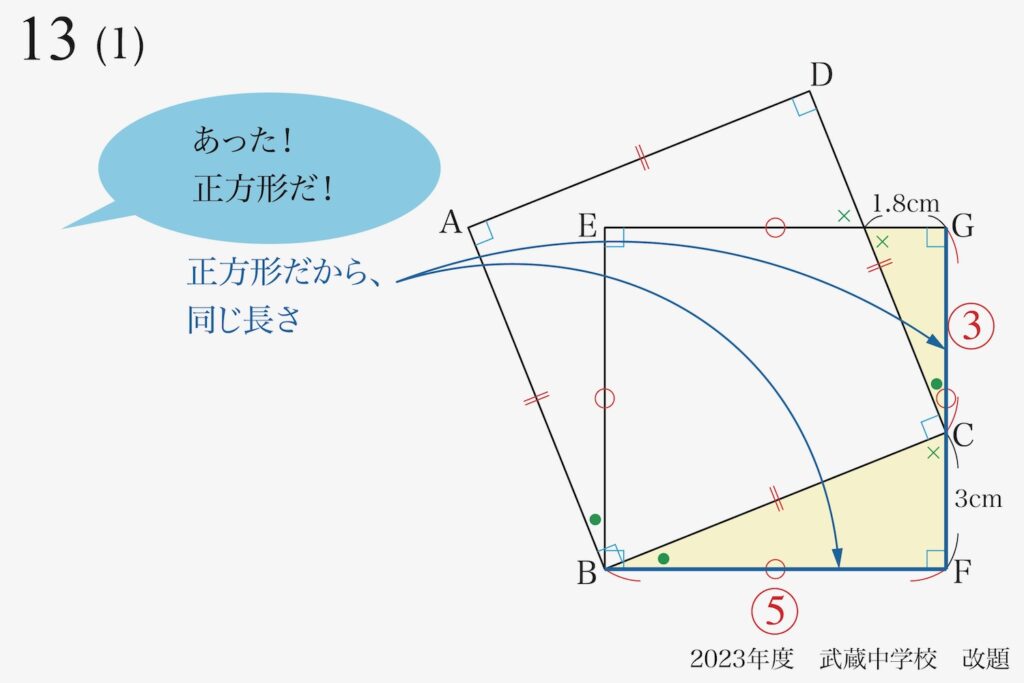
「正方形=四つの辺の長さが同一」という条件は、非常に強い条件です。

非常に特殊な正方形という条件が出てきた時は、「辺の長さが同じ」と考えるようにしましょう。

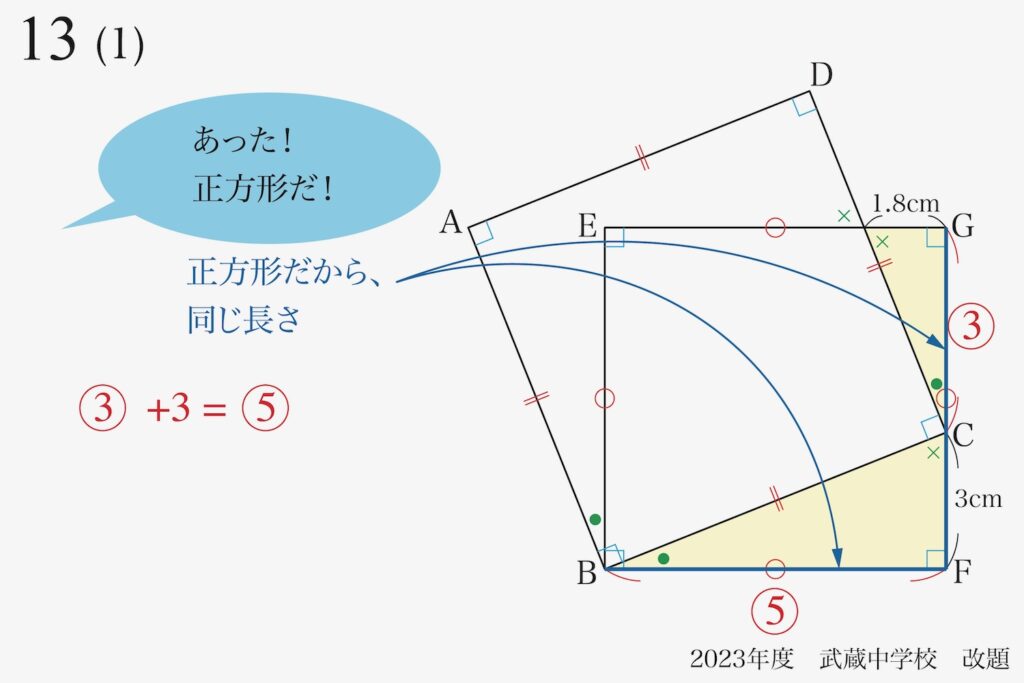
図形のポイントが掴めたら、立式（式を立てる）しましょう。

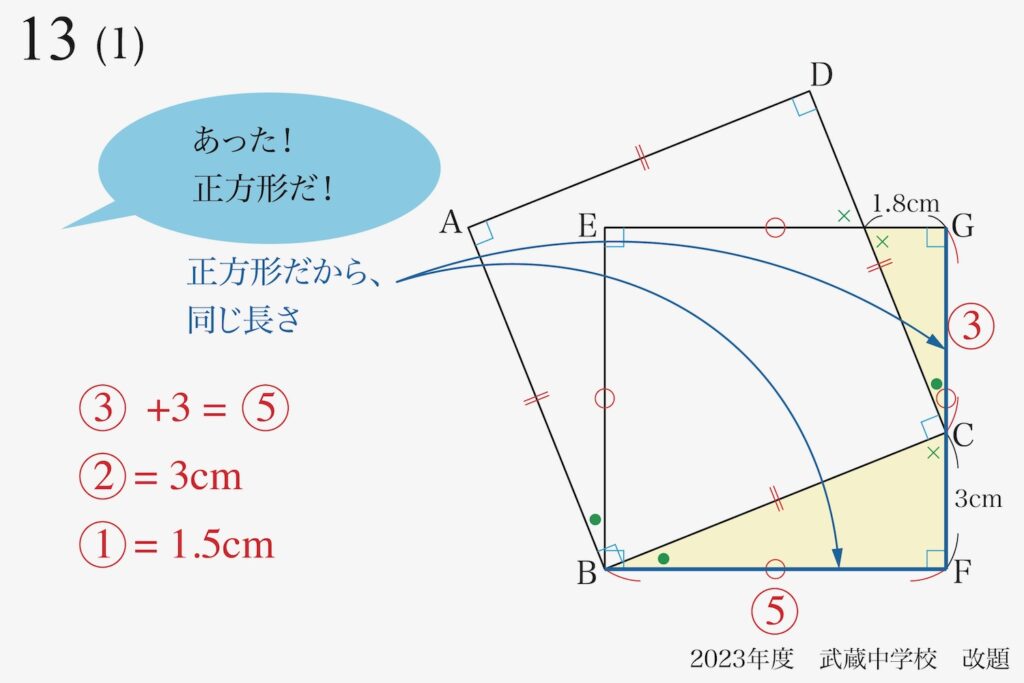
ここまでくると、図形問題から数式の問題になります。

「分からない辺の長さ」の基本的長さ①が分かりました。

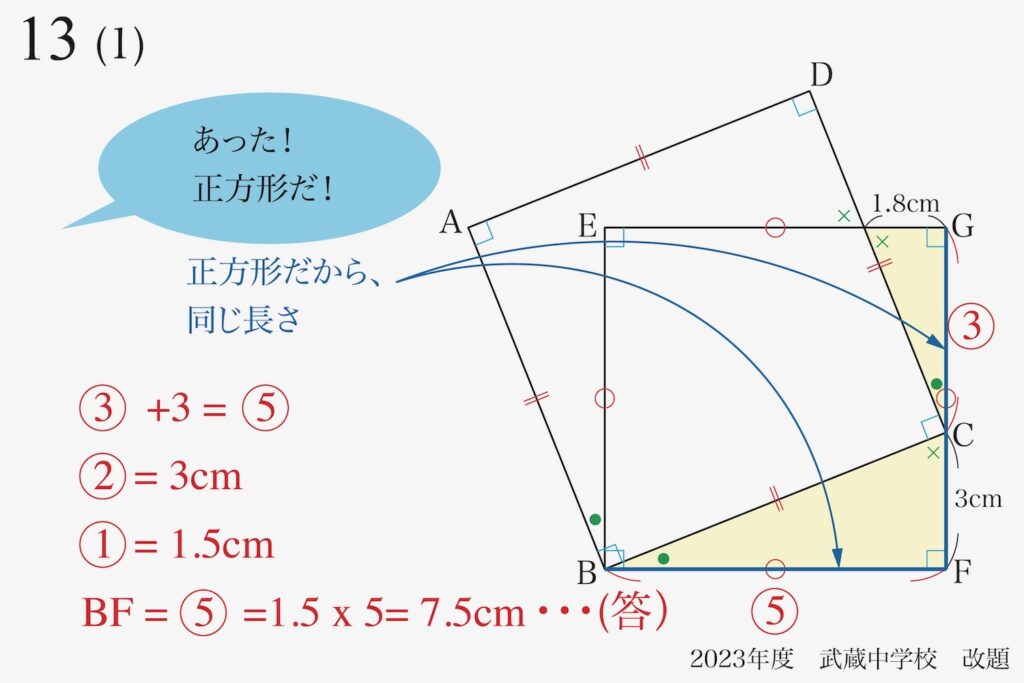
これで解答に至りました。

今回は「相似比の分かる一組の相似形」発見が大きなポイントでした。

そして、問題を解く鍵は「相似形の相似比と正方形」でした。

「相似比」は自分で求めたことで、「正方形」は問題の条件です。

図形問題に限らず、文章題などでも「問題の条件」は非常に大事です。

問題の難易度によりますが、「問題の条件をどう活かすか」が難しいこともあります。

文章題では多くの場合「数字や量・長さ」で表現されている「問題の条件」。

対して、図形問題では正方形・正三角形・正六角形・・・など条件が「隠れている」こともあります。

上の「正方形だから辺の長さが同じ」は「言われれば当然のこと」ですが、気づかないことがあります。

このように「図形の基本性質」が「問題を解く鍵」であることがあります。

算数・数学は、「何か大事なポイント」が分かると一気に見通しが良くなります。

特に図形問題は「相似比の分かる一組の相似形」などが分かったら、

こう考えて、

「もう少しで出来る」と考えるようにしましょう。

(1)はこの考え方が基本ですが、もう一つ考え方があるので、別の機会にご紹介します。

次回は下記リンクです。