前回は「上手い・下手を気にせず描く〜描いて理解・「解答を見てわかった気持ち」にならない姿勢・「見よう見まね」で描いてみる姿勢・「学ぶ」は「真似ぶ」から・上からなぞってみる姿勢・拡大して図形をしっかり理解〜」の話でした。
算数の学力の伸ばし方:様々な図形と様々な解き方
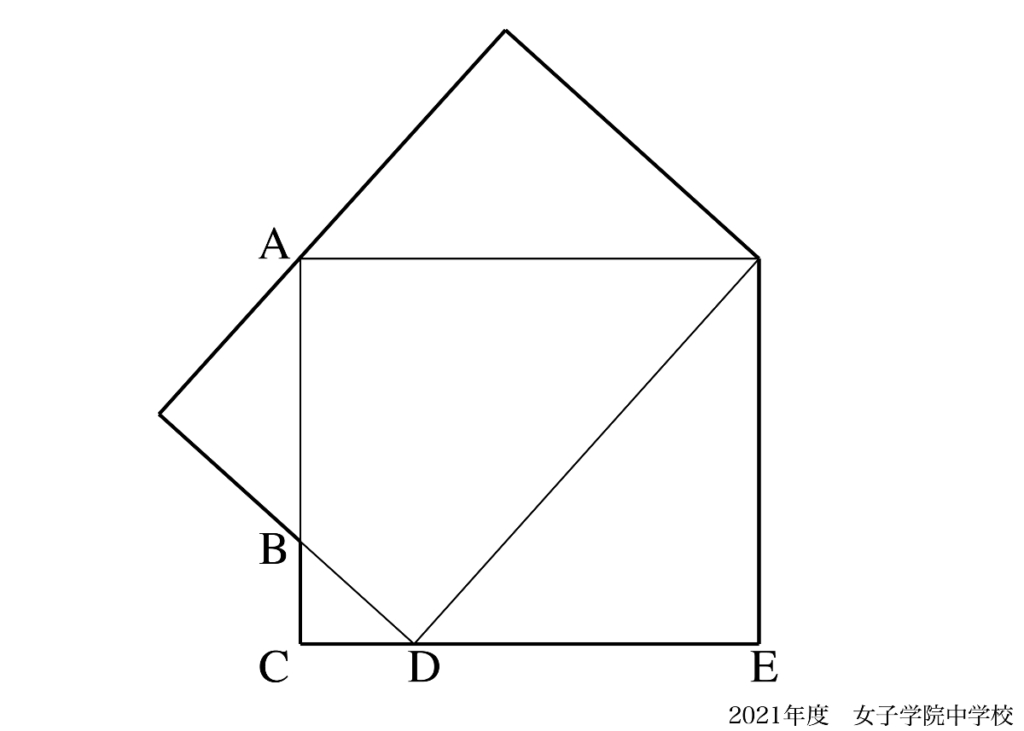
今回は「算数の学力の伸ばし方」の話で、図形問題を例に考えましょう。
上の図形のように「二つの長方形」が登場する図形問題を考えてみましょう。
このように「複数の似た図形」が登場する図形問題は、かなり多いです。
 出題者
出題者ここに三つの正方形が
あります・・・
「複数の似た図形」は、当然のことですが「似た・類似した性質」を持っているので、



この類似した性質から、
ここに大事なポイントが隠れている・・・
類似性を追求すると「大事なポイント」が出てくることが多いからです。
上の図形問題では、「二つの長方形の半分」となる補助線がポイントでした。
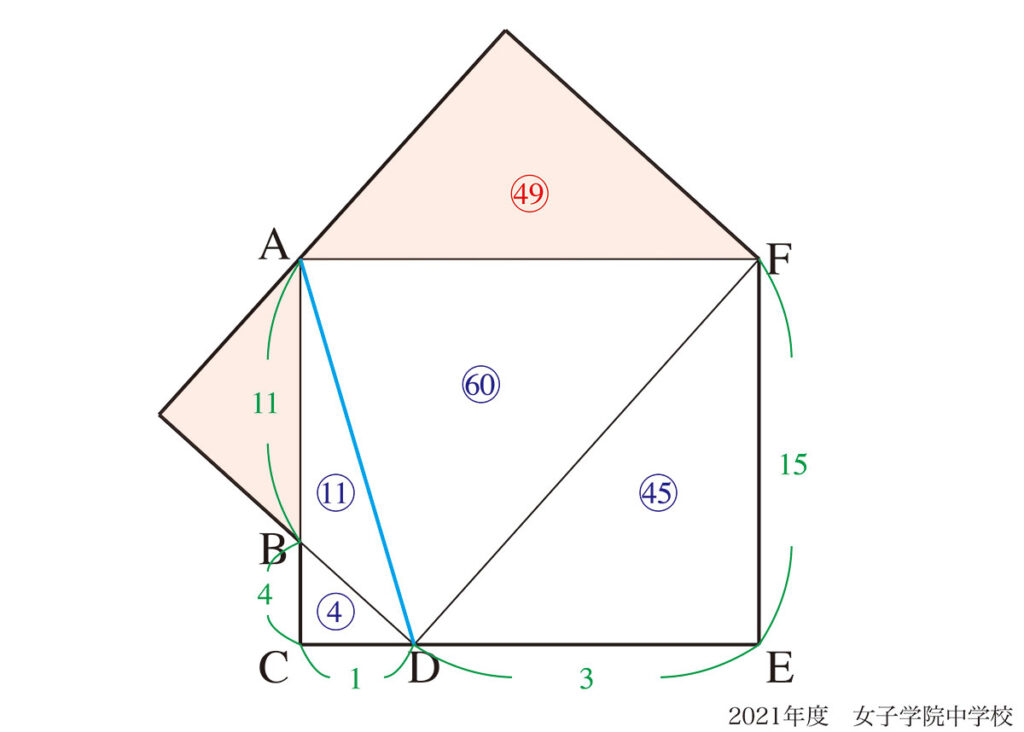

補助線のコツの話を、上記リンクでご紹介しています。
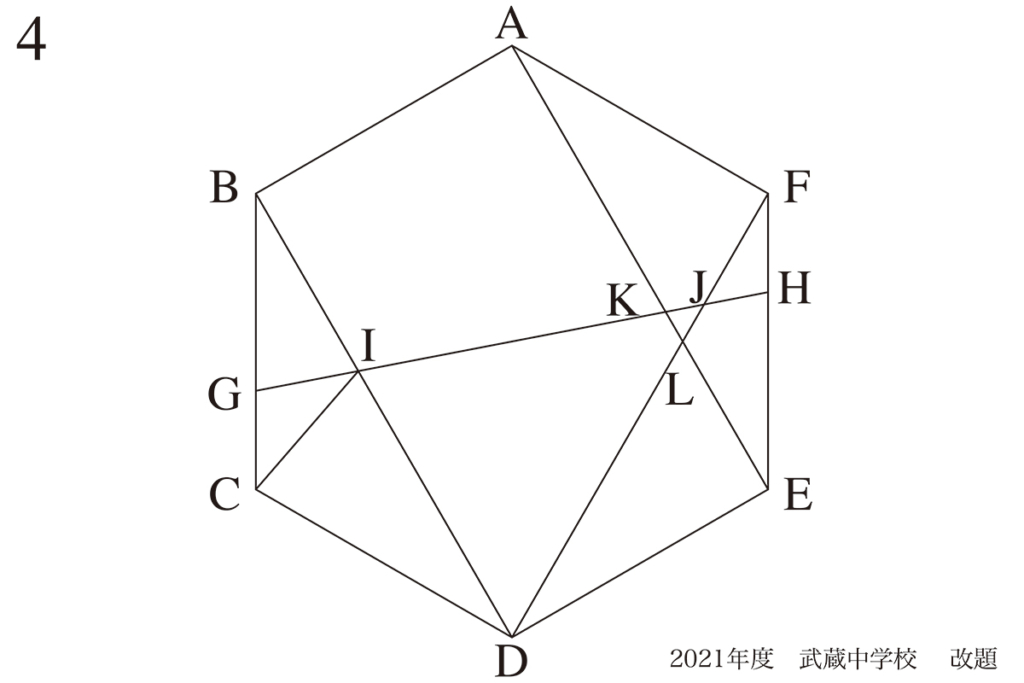

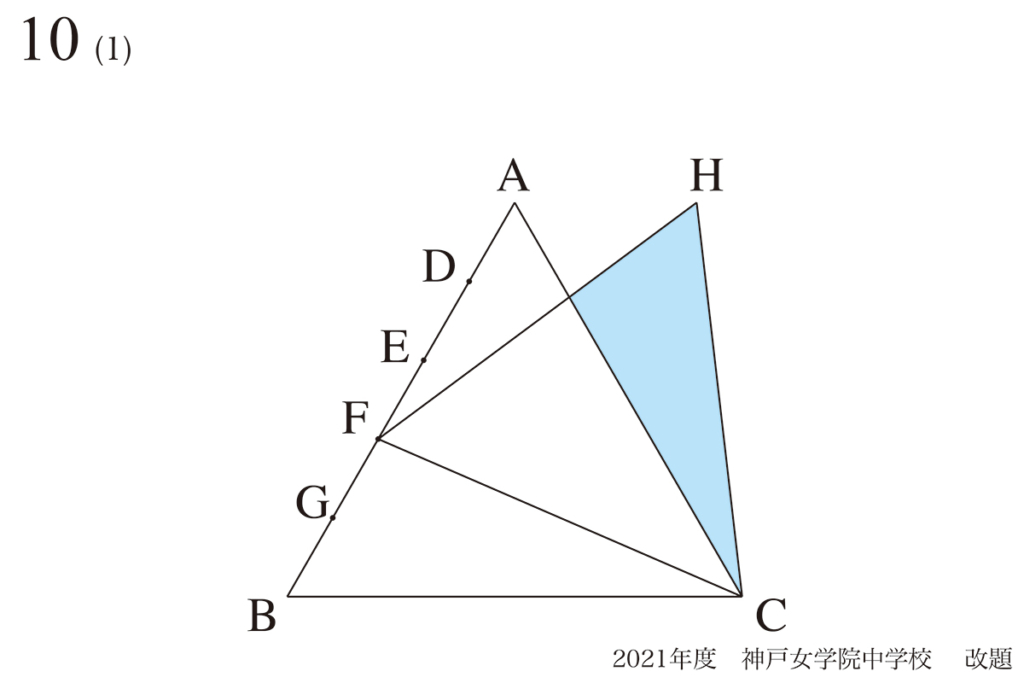
正六角形の問題を考えた時は「正六角形の中心・対象軸」を考えることがポイントです。
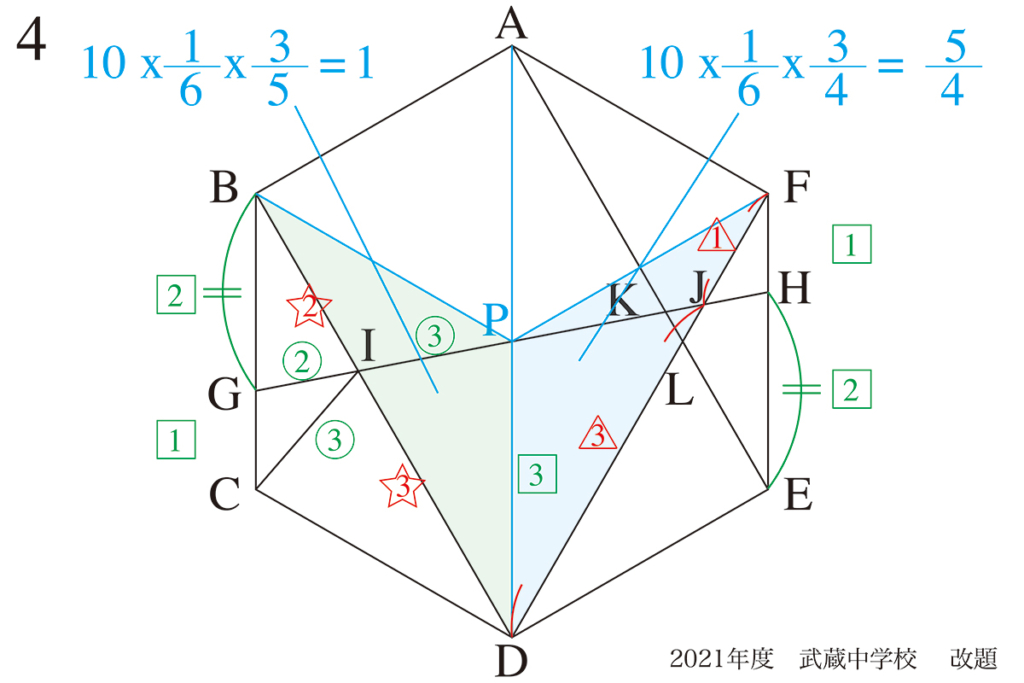

・一気に考えるのではなく、分かるところから徐々に考えてゆく
・図形に「わかっていること」を描いて整理する
正六角形の考え方を、上記リンクでご紹介しています。
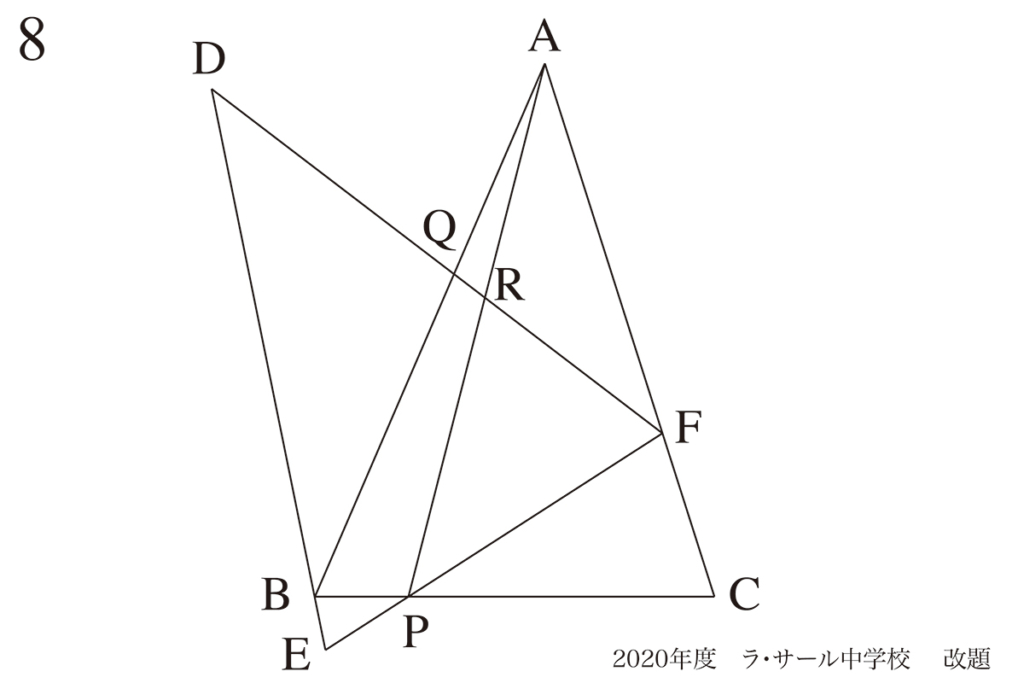

回転する図形では、「回転する前後の図形は同じ」という事実から、同じ角度・同じ辺を考えることがポイントです。
・回転した図形も、元の図形も「同じ図形」であることを強く認識
・「同じ辺の長さ」と「同じ角度」を図形に描きこむ
・たくさんの「同じ角度」から、相似形を見つけて相似比を考える
移動する図形のコツを、上記リンクでご紹介しています。
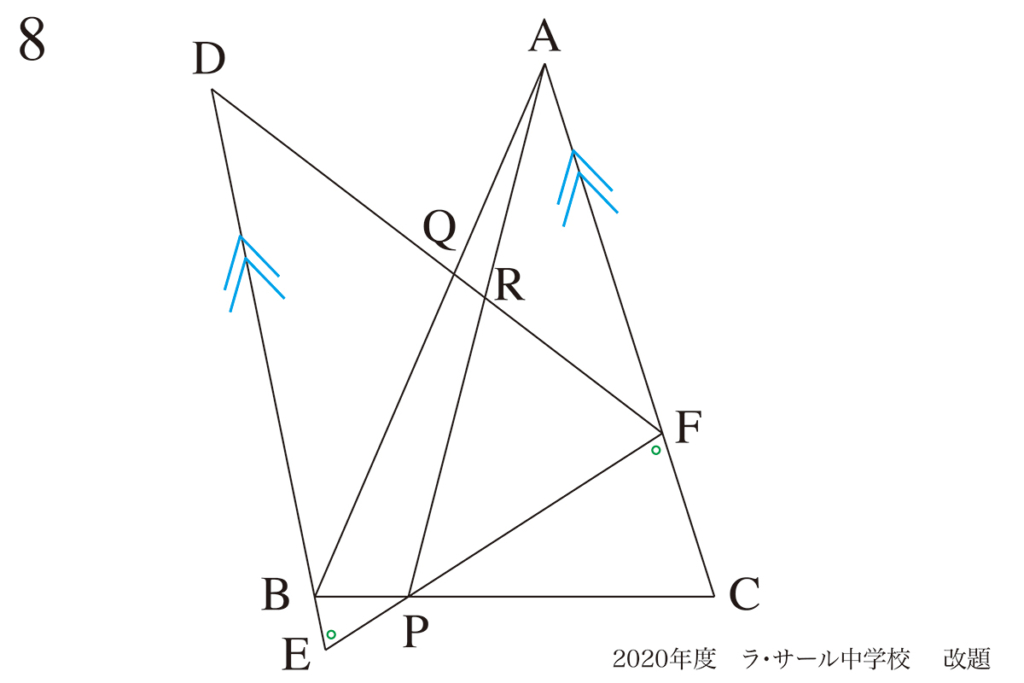

回転する図形の問題を考える時には、



回転するということは、
元の図形と同じだから・・・
「同じ角度=錯覚が同じ」から平行な線を見つけることがポイントです。
・平行な直線同士の錯角は同じ
・錯角が同じ直線同士は平行
平行な線が見つかれば、「相似形がたくさん見つかる」ので問題が解けるようになります。
上記のような、長方形・正方形・回転する図形以外にも、



図形問題って、
たくさんの種類やパターンがあるね・・・
図形の問題は沢山の問題・種類・パターンがあります。



これらの問題を出来るだけ解いて、
全部の解法を頭に入れないと・・・



とても大変・・・
キリがないような気がする・・・
様々な特徴的な図形の基本的性質を考えれば、それに応じて様々な図形の組み合わせなどが考えられます。
さらに、折り返し・回転などの「一種の操作」を加えれば、図形問題は「無限に作れる」でしょう。



はあ・・・・・
どこまで勉強したら、出来るようになるんだろう・・・
中学受験生は大変です。
同じように考える姿勢:大事なポイントを意識して学力アップ






これらの「全然違うように見える」図形問題の解き方。
ところが、図形問題の解き方には、非常に似ている部分がありませんか。



似ているところ?
補助線を引く、かな?



そう言えば、大抵
相似形を考えるね・・・
「補助線を引く」という「解くプロセス」に共通点があります。
一方で、それらは「問題の性質」とは少し異なります。
図形問題では、平行・相似形が頻繁に登場し、「平行と相似形を考えれば解けることが多い」です。



確かに
そうだね!
・直線が互いに交わらない
・直線が互いに「全く同じ向き」を向いている
直線が「平行であること」を、もう一度考えてみましょう。
「平行な直線同士」は「全く同じ方向を向いている」ので、「絶対に交わらない」のです。
・平行な直線同士の錯角は同じ
・錯角が同じ直線同士は平行
そして「補助線で相似形を見つける」ことが大事なポイントです。
そのため「相似形を見つけることが図形問題の共通な解き方」であることを強く意識しましょう。
そして、「相似形が見つからない」ときは「相似形を自分で作る」姿勢が大事です。
・平行な直線のうち、一つまたは二つの直線を延長する
・平行ではない直線を延長して、新たな交点を作ると相似形が出てくる
このように考えると、これらの図形問題には「似ている点」がたくさんあります。
そして、見方によっては、「どれも似ていて、同じような問題」に見えてきませんか。



確かに似ている
かも・・・



同じような
考え方も多いね・・・
このように「図形問題」ならば、「相似形を考える」という大事なポイントを意識しましょう。
横断的に考える:「問題ごとの解法」より大事な「共通する考え方」

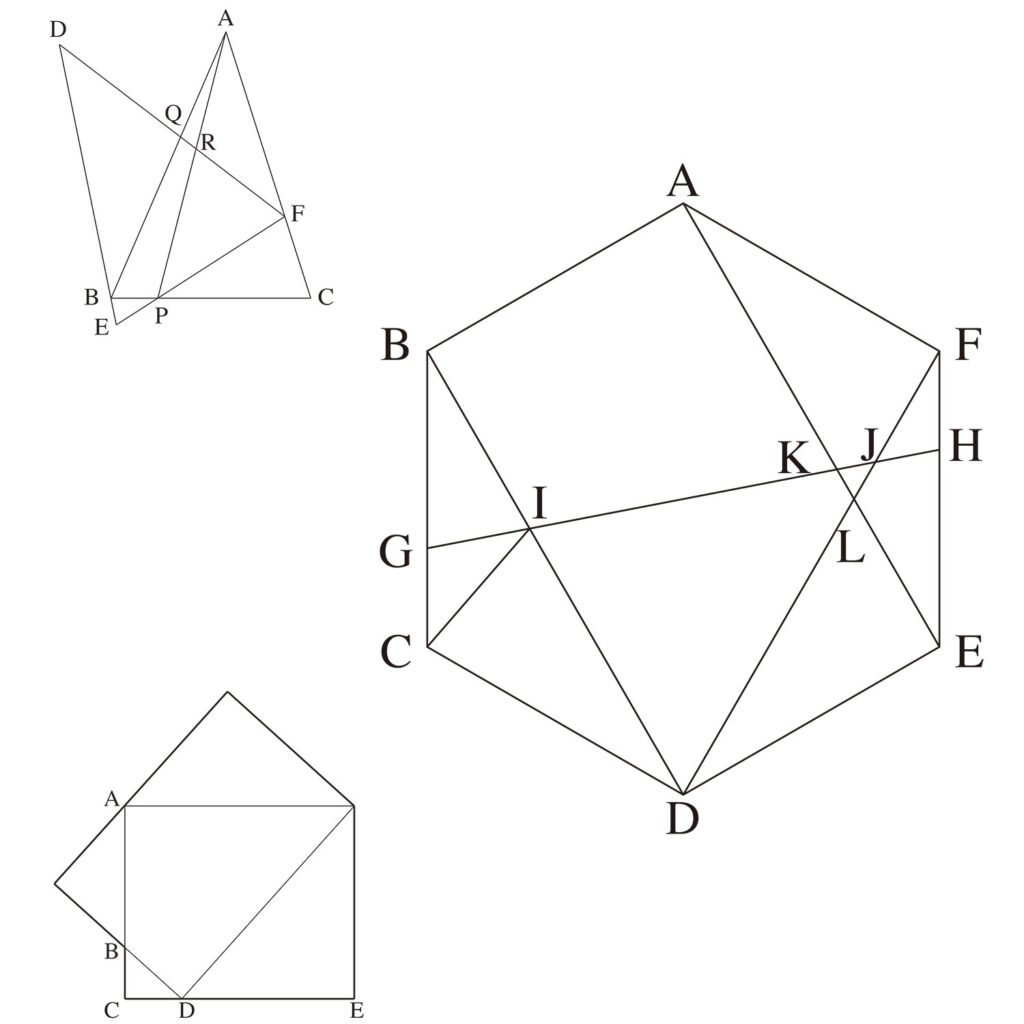
いくつかの図形が重なると「難しく見える」ことが多いです。
こうした図形問題では、大抵小問に分かれています。
・前の問題が後の問題のヒント・鍵になっていることが多い
・「前で考えたこと・解いた結果」は常に意識
小問では「前で考えたこと・解いた結果」は、次の問題のヒントとなることが多いです。
そこで、全体的な流れを意識して問題を解くようにすると、考えた方がより身につくでしょう。

図形問題でも文章題でも同じ面があります。
そして、旅人算・ニュートン算・てんびん算などの「算数的考え方」にも「類似した考え方」があります。
それらの「類似した考え方」をしっかり学ぶと、



このあたりは
「似た考え方」かも・・・
問題数を沢山やらなくても、算数の学力が上がるでしょう。



この問題集を
全部やらなきゃ!
こう考えるのではなく、一題一題しっかり考えて、



この問題の、この考え方は
応用が効きそうだな・・・
このように「理解して考えながら勉強する」と、応用力が上がり様々な問題が解けるようになるでしょう。
問題ごとの解法ではなく、大事な「共通する考え方」を身につけるように勉強してみましょう。
特に秋から直前期の「沢山学んだ後」は、たくさんの解法が頭にストックされているので効果的です。
次回は下記リンクです。





