前回は「回転移動する図形の考え方〜回転すること・同じ図形が2つあること・問題 8〜」の話でした。
今回は(1)の解法です。
問題 8(再掲載)

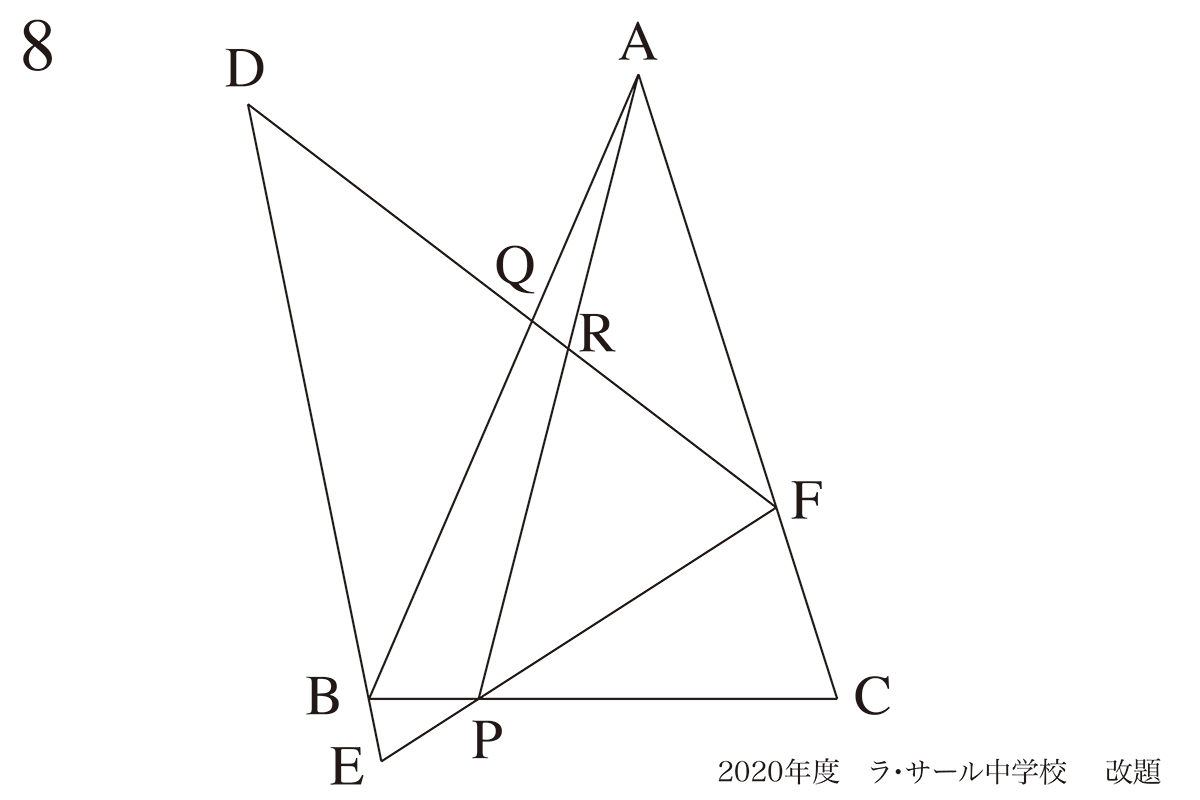
移動・回転する図形の問題:「同じ辺」と「同じ角度」に注目
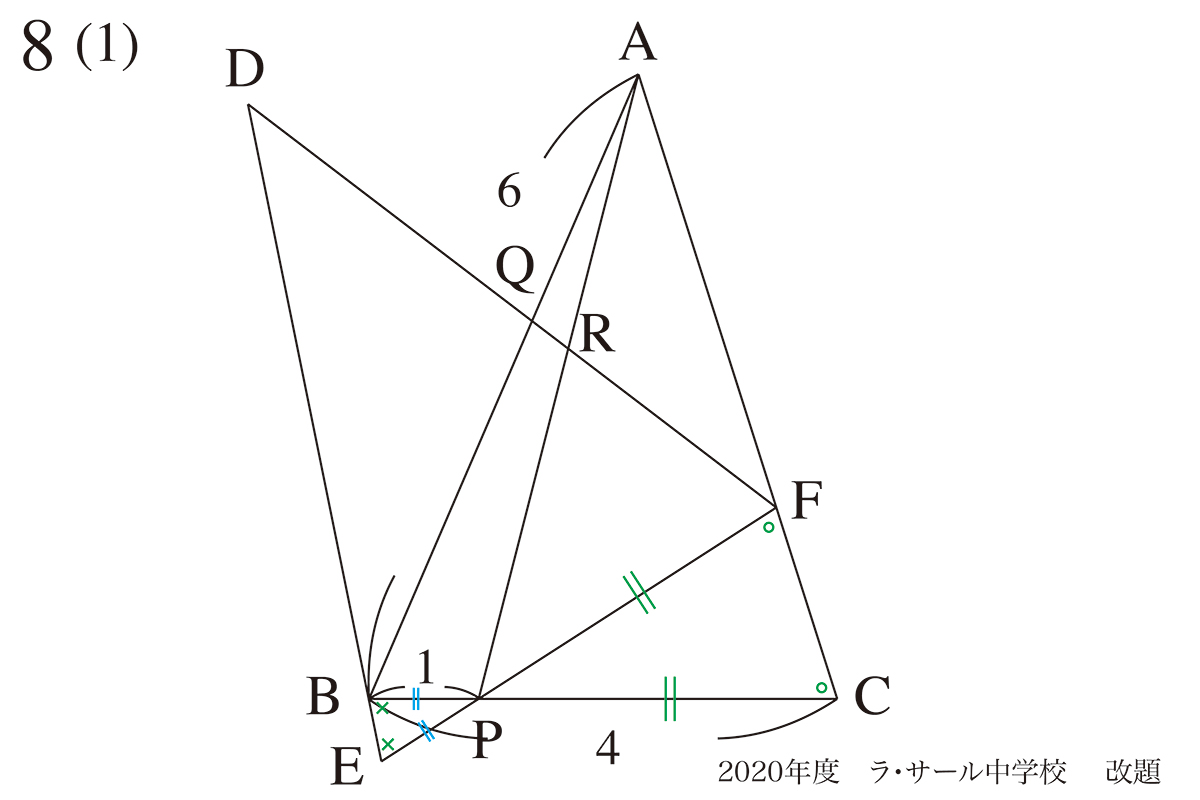
図形を「回転・折り返す」問題は、まず「同じ辺」「同じ角度」を考えましょう。
この問題の場合、回転させて辺・点は移動しています。
辺・点は移動していますが、回転軸となる点Pに関わる辺の長さが同じです。
「同じ辺の長さ」や「同じ角度」をどんどん図形に描いてゆきましょう。
そして、「同じ長さの辺」「同じ角度」をしっかり押さえましょう。
・回転した図形も、元の図形も「同じ図形」であることを強く認識
・「同じ辺の長さ」と「同じ角度」を図形に描きこむ
・たくさんの「同じ角度」から、相似形を見つけて相似比を考える
上のように、二等辺三角形が二つ見えてきます。
△PFCと△PEBが二等辺三角形で、同じ角度があります。
図形に「分かること」を描いて「大事な性質」を理解
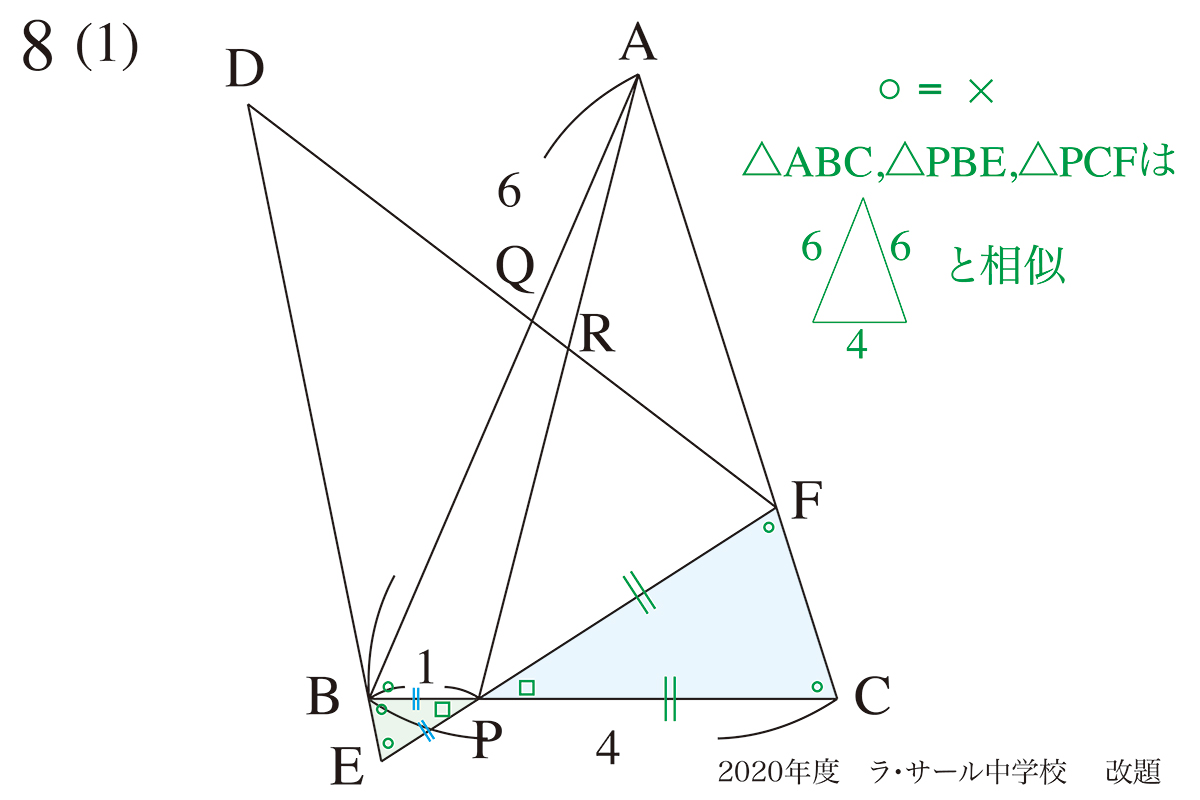
そのため、先ほどの○とxは同じ角度で、△PFCと△PEBは二等辺三角形でさらに相似です。
角BPEと角CPFは、「○とxは同じ角度だから同じ」または「対頂角だから同じ」です。
回転させているので、角BEPと角ABCが同一です。
そこで、△ABC二等辺三角形かつ△PFCと△PEBと相似です。
 男子小学生
男子小学生同じ角度から、
次々と大事な性質が分かってくるね!



なんだか
不思議な感じ・・・
ここが、本問題の最重要ポイントです。
「回転」「折り返し」の図形問題は、このように「同じ角」「同じ辺」を描いてゆくようにしましょう。
そして、「大事な性質が見える」ようにしましょう。
こういう回転・折り返しの図形問題は、まず



どこが
同じかな?
このように「同じ角度・辺」を考えましょう。
すると、全体像が見えてきて、考えやすくなります。
図形問題は「平行」な辺がポイント
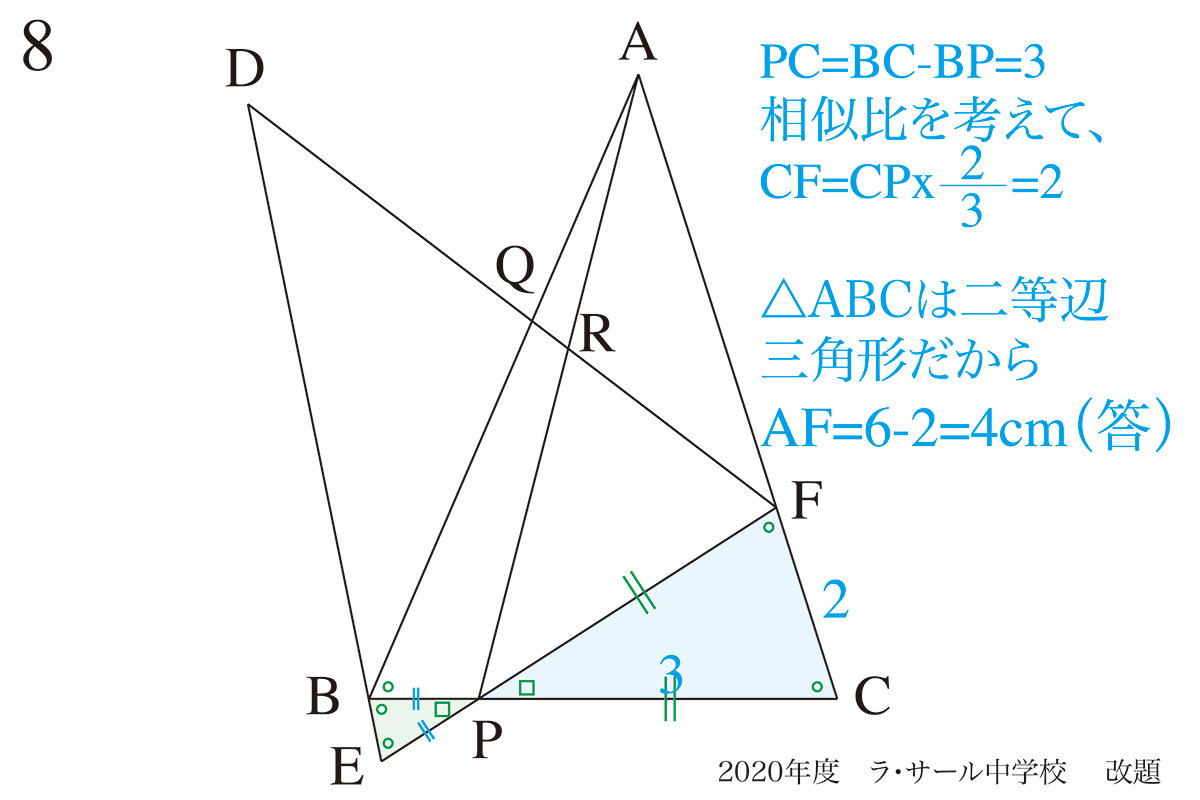

上のように、相似比から長さが求まります。
(1)は「同じ辺」「同じ角度」を押さえられれば、一気に進みます。
(2)は相似図形を考えて、平行な辺を押さえることが大事です。
平行な辺・直線の性質をもう一度復習しましょう。
図形問題では「平行な辺・直線」が非常に大事です。
本問の図形で「平行な辺」は見えますか。



平行な辺は
どこかな?
相似図形は大事なポイントで、平行な辺を見つけることが一つの突破口になります。
(2)解法は次回ご紹介します。
次回は下記リンクです。


