前回は「電気・回路の実戦的考え方 2〜回路の形と電球の配置・算数の問題と理科の問題は友達・対称性があること・形・図形に安定感がある・対称性から分かること・点から点の下がる電圧・状況を整理する姿勢〜」の話でした。
対称軸と中心と重心：モノの最も重要な性質
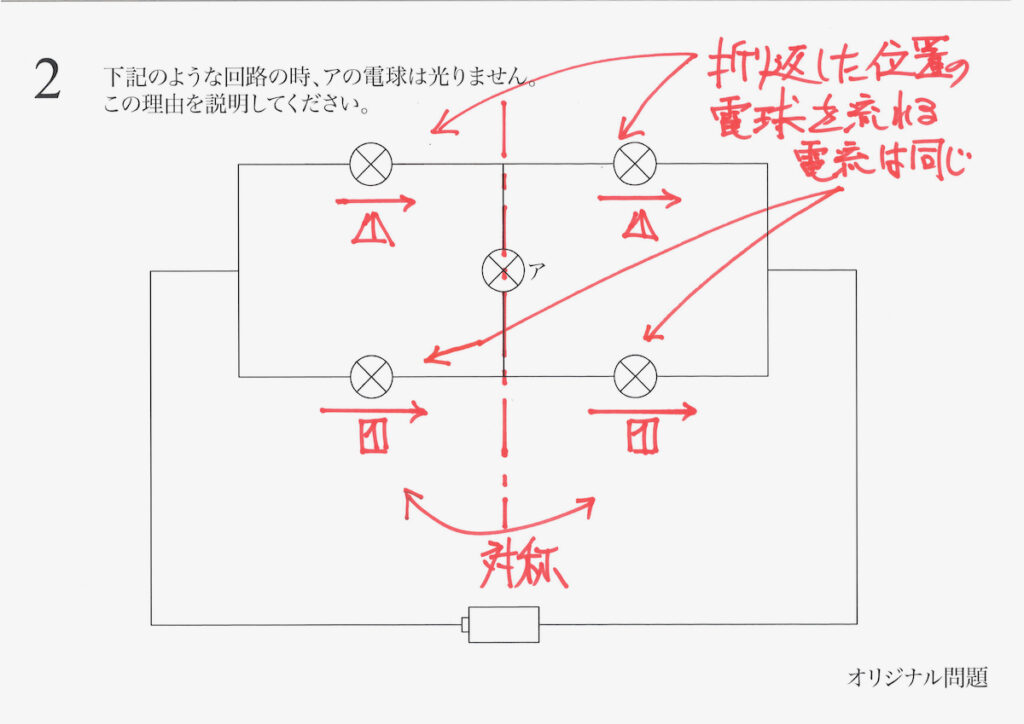
前回は、対称性から「同じ電流の大きさ」が分かりました。
このように「対称性を考える」と、算数や理科は非常に見通しが良くなります。
男子小学生対称性って、
大事な性質なんだね！
女子小学生これからは、対称な形や図形が
あったら、気にしよう！
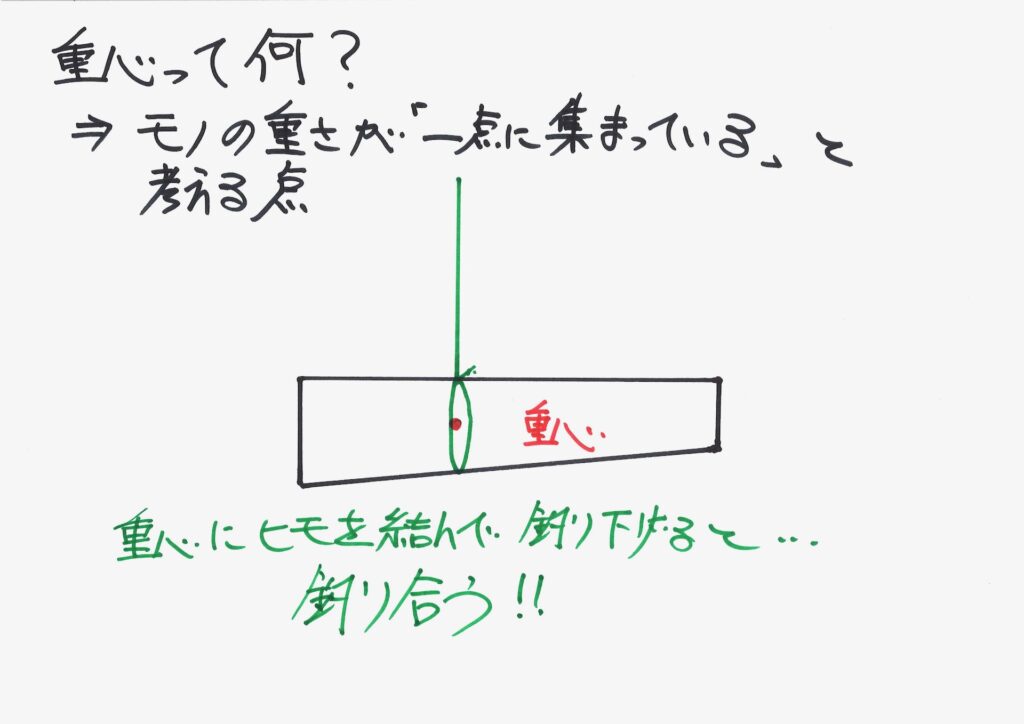
重心もまた「対称となる点」の一つです。
重心は、物理的・数学的に「定義（決まりごと）」がありますが、「中心」というイメージで良いです。
・モノの重さが一点に集まっている点
・重心一点に、モノの重さが全部集まっている
・モノの中心
モノ・物事の中心・重心は、極めて大事で「モノ・物事の最重要な部分」と言っても良いでしょう。
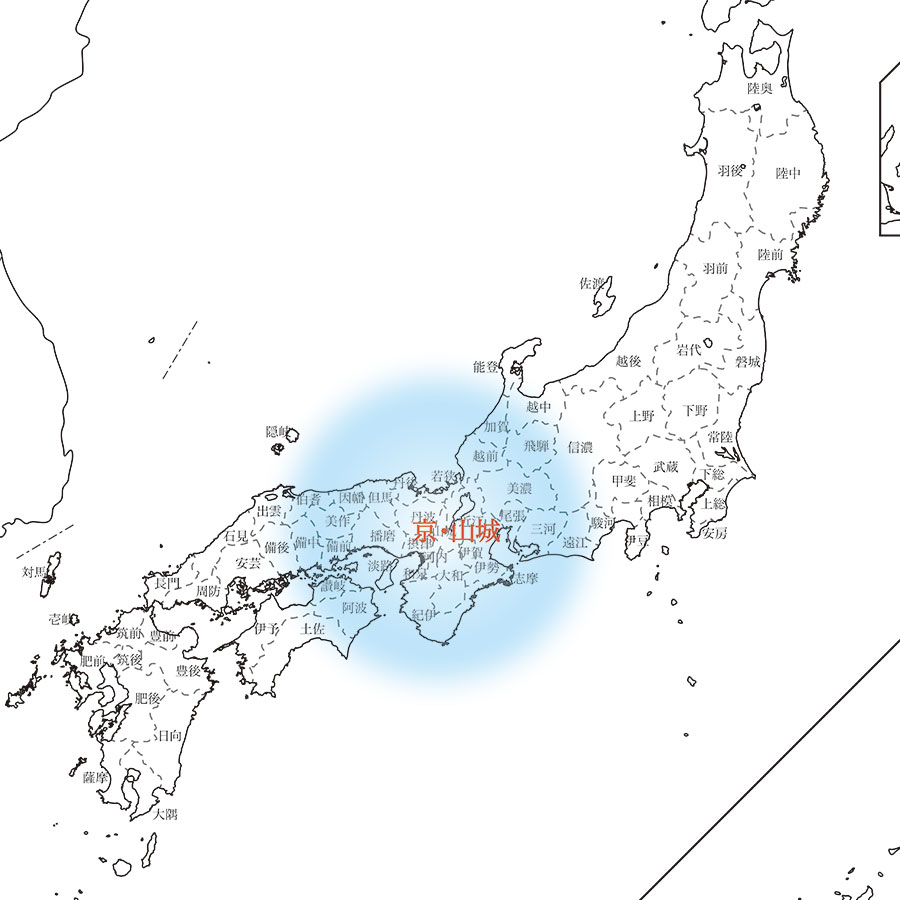
現代とは異なり、京・山城が「日本の精神的中心」であり続けました。
「昔の国の名前」にも、「中心・重心である京の影響力」がありました。
日本の旧国名に関する話を、上記リンクでご紹介しています。
現代、東京が中心であり「東京一極集中」と言われる日本。
その現代日本においても、私たち日本人にとって「京都は特別な、格別な場所」です。
女子小学生前に、京都に家族旅行で行ったけど、
なんだか他の街とは違うように感じた・・・
男子小学生京都の街って、
他の街とは雰囲気違うね！
「一都二府」とまとめられる東京都・京都府・大阪府ですが、京都府の存在感は格別です。
モノの最も重要な性質である対称軸と、中心・重心に気づいたら、
女子小学生対称性を考えたり、
「同じもの」がないか、考えよう！
地道に計算して考える姿勢
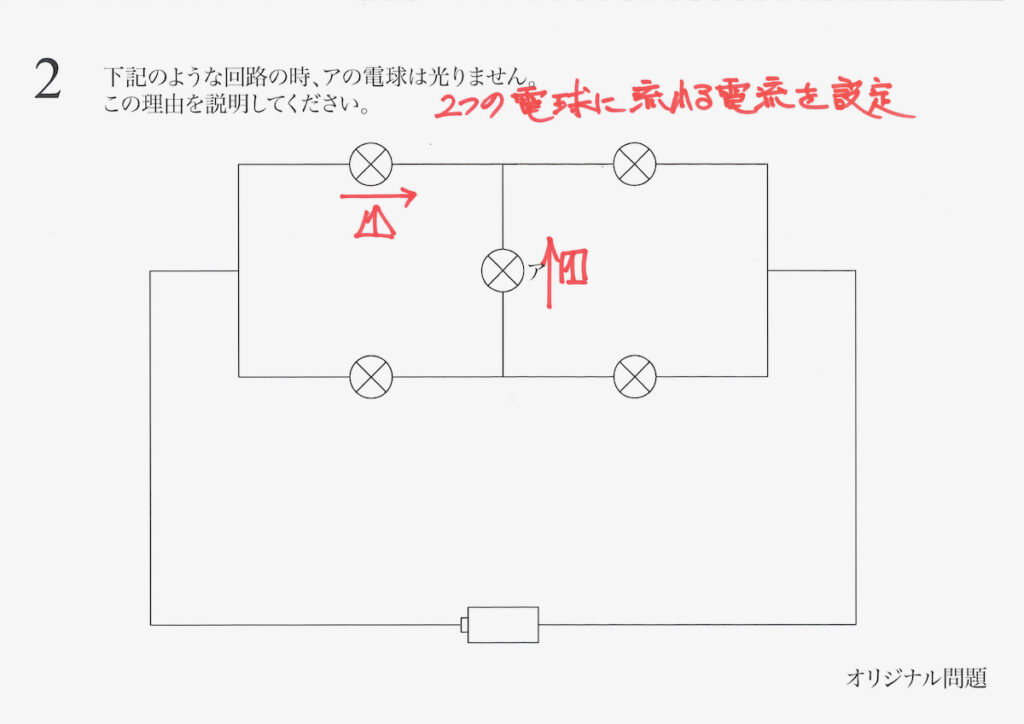
今回は、「対称性に気づかなかった」とします。
男子小学生対称性に気づかなかったら、
解けないんじゃないの？
理科・算数では「何かに気づく」ことが「問題を解く鍵」であることが多いです。
「問題を解く鍵」は非常に大事なポイントですが、「それが分からなくても解ける」場合があります。
女子小学生「解く鍵」が分からなくても、
「解ける」なら、嬉しいかも！
「ポイントに気づかない」と「時間がかかる」ことが多いですが、「解ける」ことも多いです。
今回は、地道に計算して考えましょう。
上の図のように、分からない電流を二つ設定します。
この設定する電流は、この二つではなく、他の二つでも良いでしょう。
中学入試では、大抵の回路は「分からない電流」を一つ、または二つ考えれば出来ます。
高校入試・大学入試では、「分からない電流」が3つ以上になることもあります。
それでも、「3つ未知数を設定」すれば、大抵の問題は解けるはずです。
この後、「合流する電流」「別れる電流」「電圧（降下）」の三つを考えます。
・電流が合流する点で、電流を足す
・電流が分かれる点で、電流を引く
・二つの点で下がる電圧（電圧降下）を「電流x抵抗（1）」で合計する
この三つが基本ですが、まずは「合流する電流」を考えます。
電流の流れは「水の流れ」と同様に、「合流したり、別れたり（分流）」します。
「電流が合流するところ」では、川の流れと同じように「電流は和」になります。
このイメージをしっかり持ちましょう。
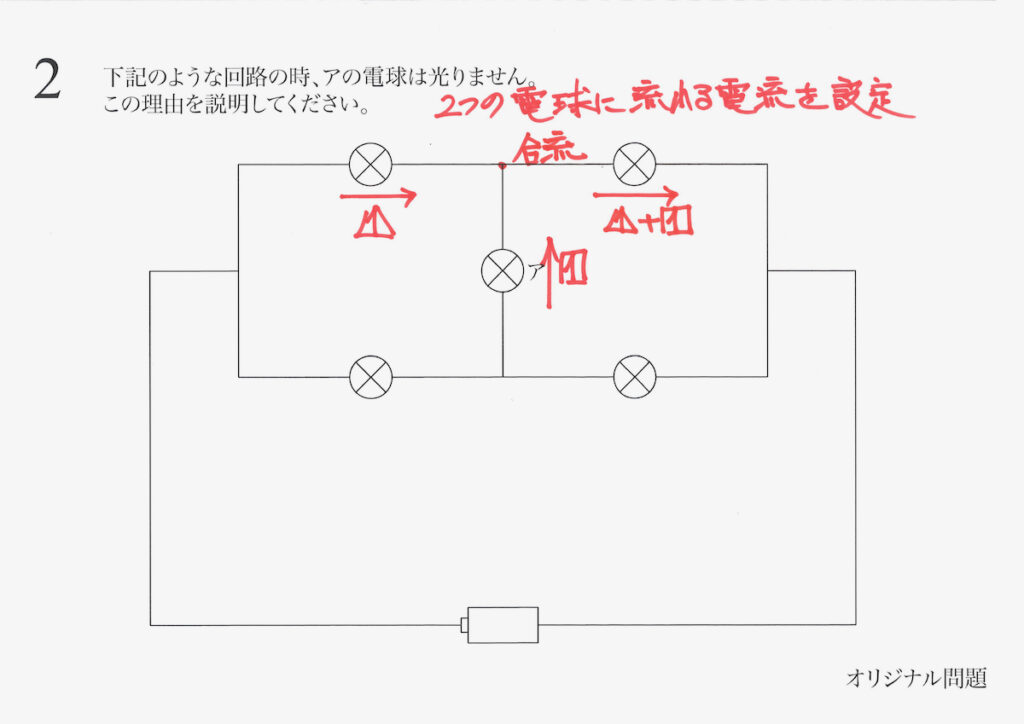
上の図のように、合流する点で電流を合計します。
男子小学生電圧が主役だから、
「電流は後回し」じゃないの？
「電圧が主役」ですが、「主役の電圧を考えるために、電流を考える」が一つのポイントです。
電流から電圧を考える：点から点で下がる電圧
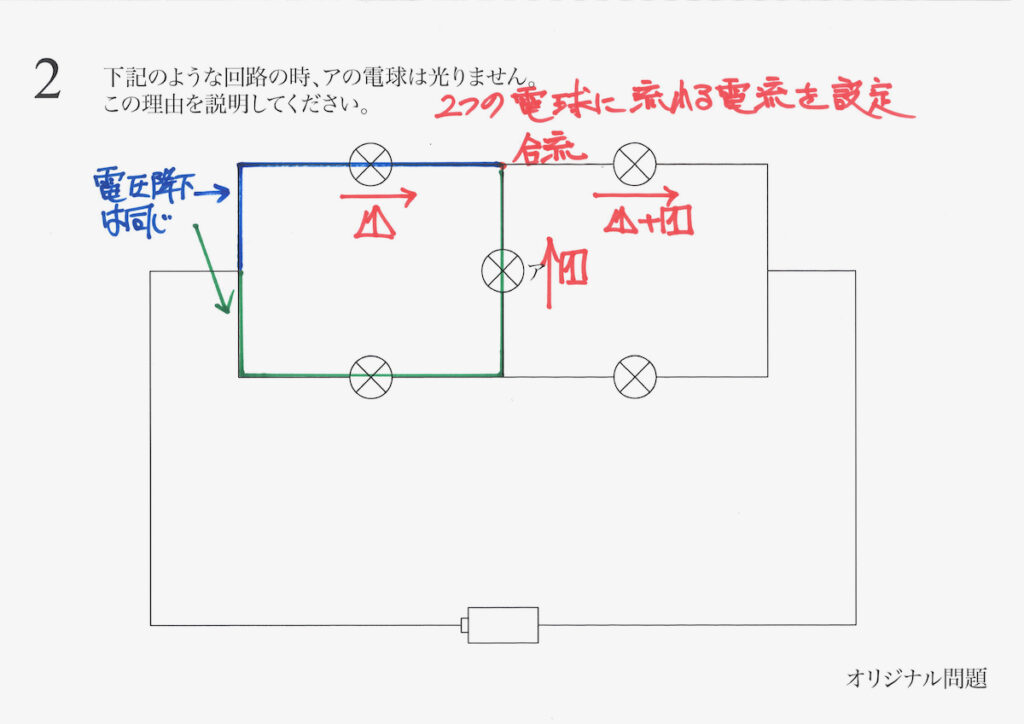
次に「電流が別れる点」を考えることもありますが、ここでは電圧を考えます。
女子小学生「電圧が主役」
の考え方だね！
上の図で、青色と緑色で「下がる電圧（電圧降下）」は同じです。
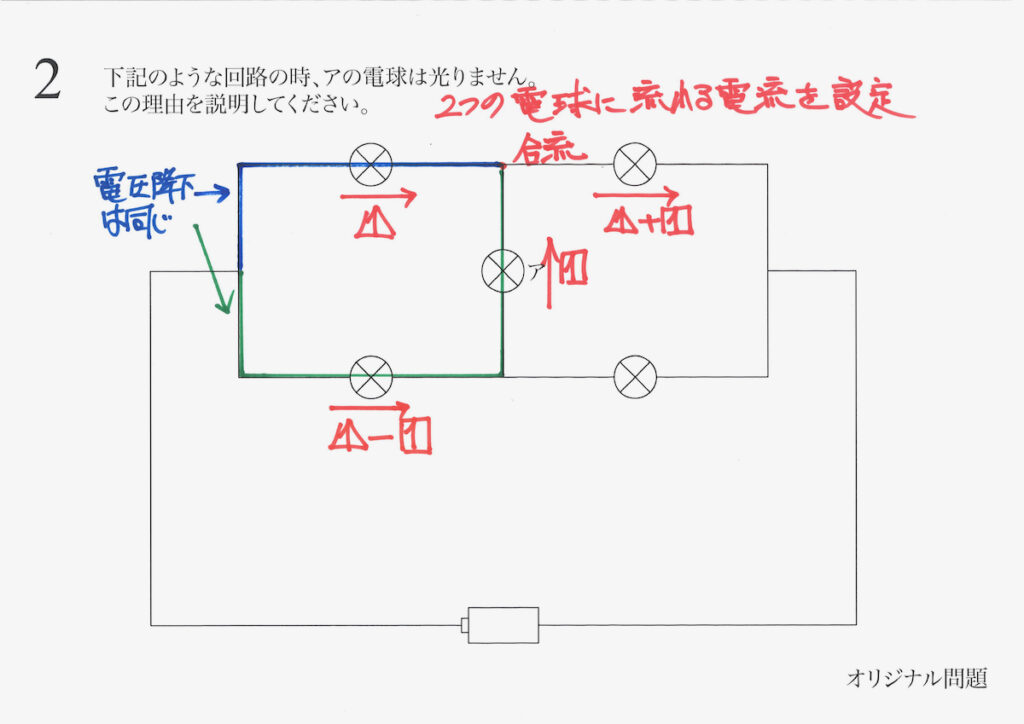
それぞれ「抵抗は1」と考えて、「電流x抵抗」である電圧（降下）が同じになります。
そこで、左下の電球を流れる電流が求まります。
男子小学生少しずつ、何かを解明するように
分かってきたね！
回路の途中まで考えたので、その後を考えてみましょう。
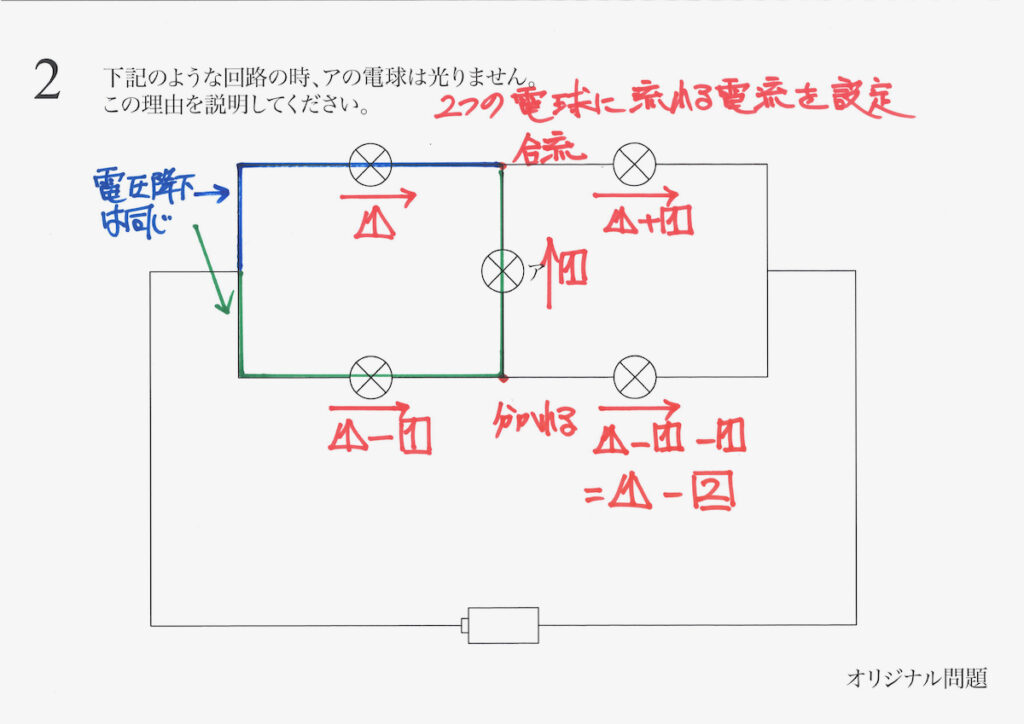
最後に、右下の電球を流れる電流は、電流が分かれます。
そこで、流れる電流を「電流の差：引き算して」求めます。
女子小学生回路を流れる電流が、
だいぶ分かってきたね！
回路全体を考える：部分から全体へ
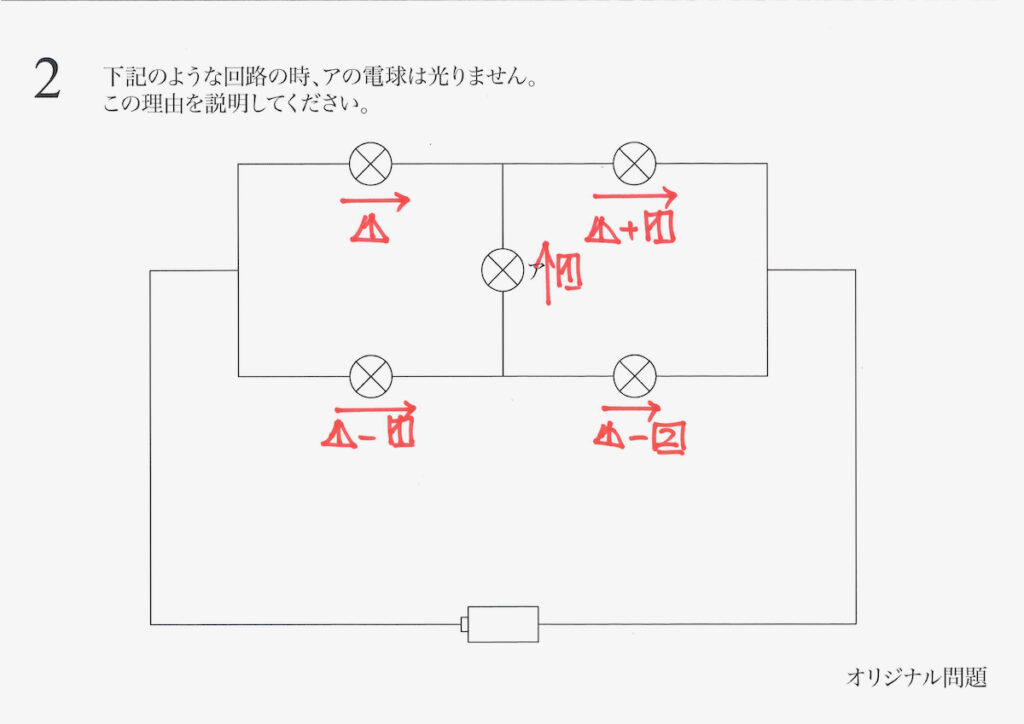
ここで、「分かった電流を一度整理」しましょう。
ここまでは「回路を部分的に考える」方法で、少しずつ電流を求めました。
そして、上の図のように、各電球を流れる電流が全て計算できました。
ここまで分かったら、最後に電流を求める時は、「回路全体を考える」方法にしましょう。
・部分的に考えて、少しずつ解明する
・部分で分かったことを活用して、全体で考えてみる
理科・算数では「部分を考える」ことと「全体を考える」ことを意識しましょう。
すると、考えが整理されるでしょう。
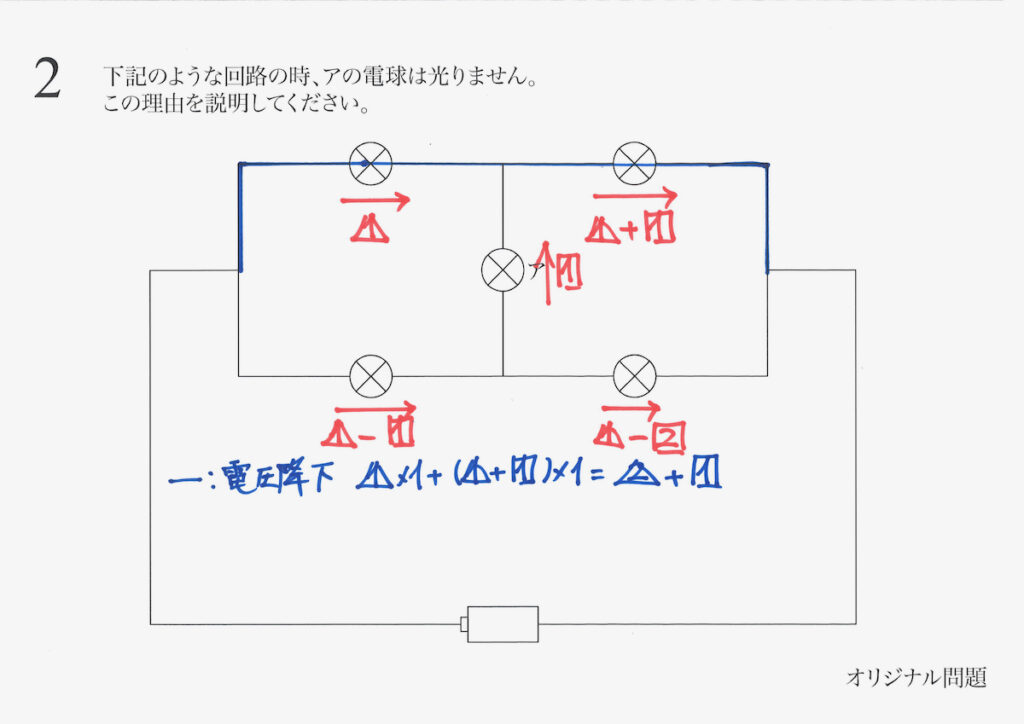
まずは、青色の経路の下がる電圧（電圧降下）を計算しましょう。（抵抗=1）
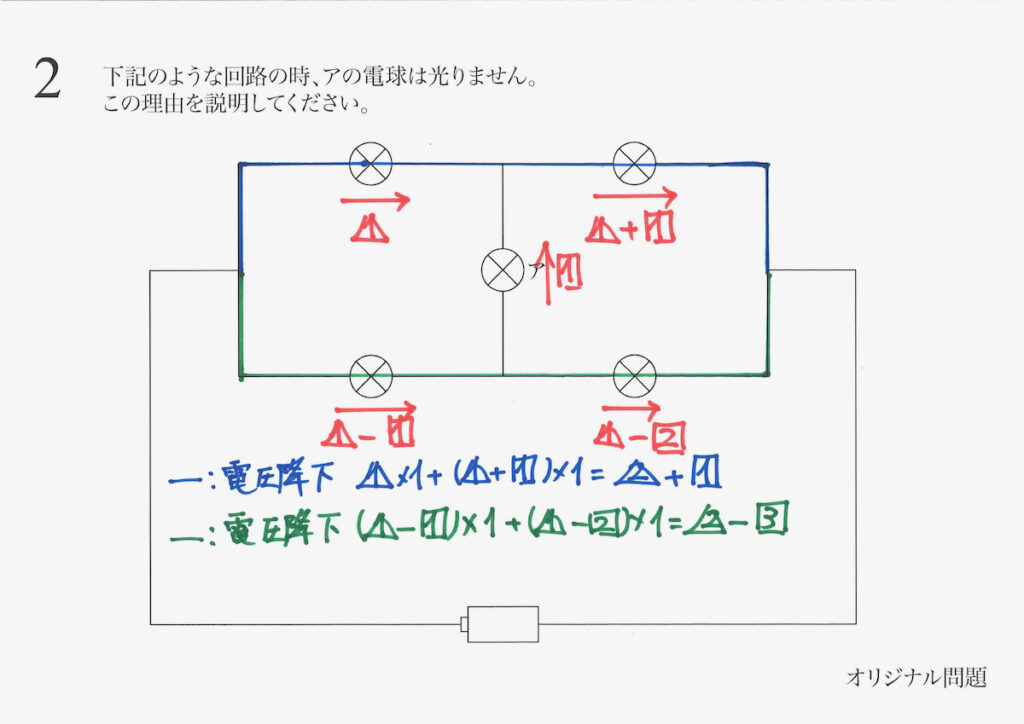
次に、緑色の経路の電圧降下を計算します。
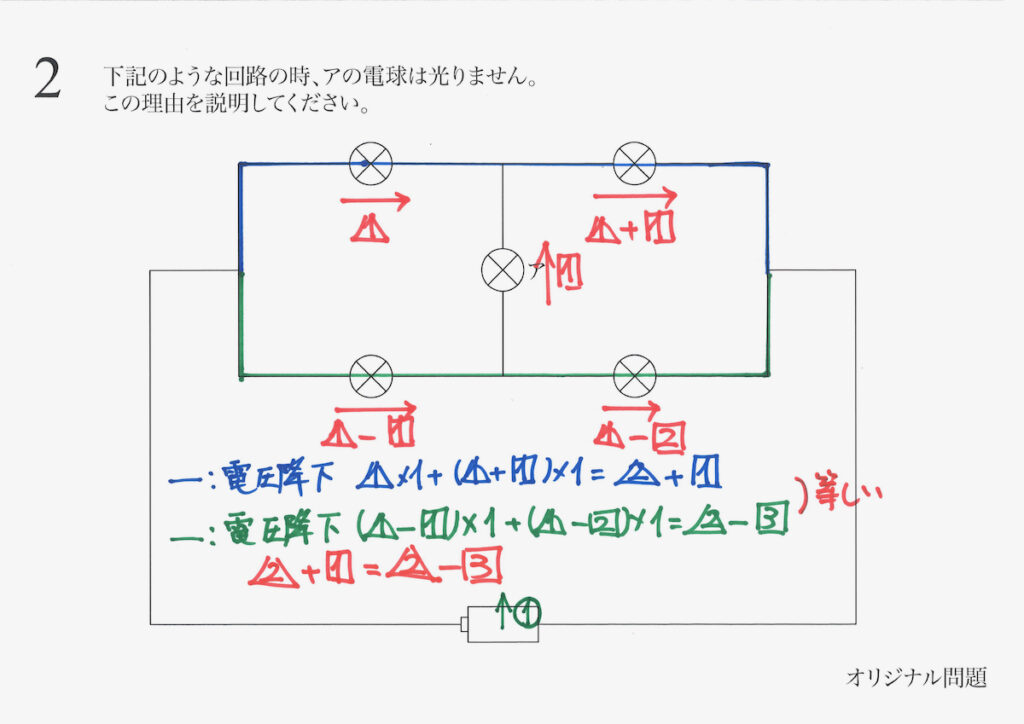
これらの電圧降下は等しいはずです。
そもそも、「電池一つで、エイッと電流を持ち上げている（電圧をかけている）」イメージです。
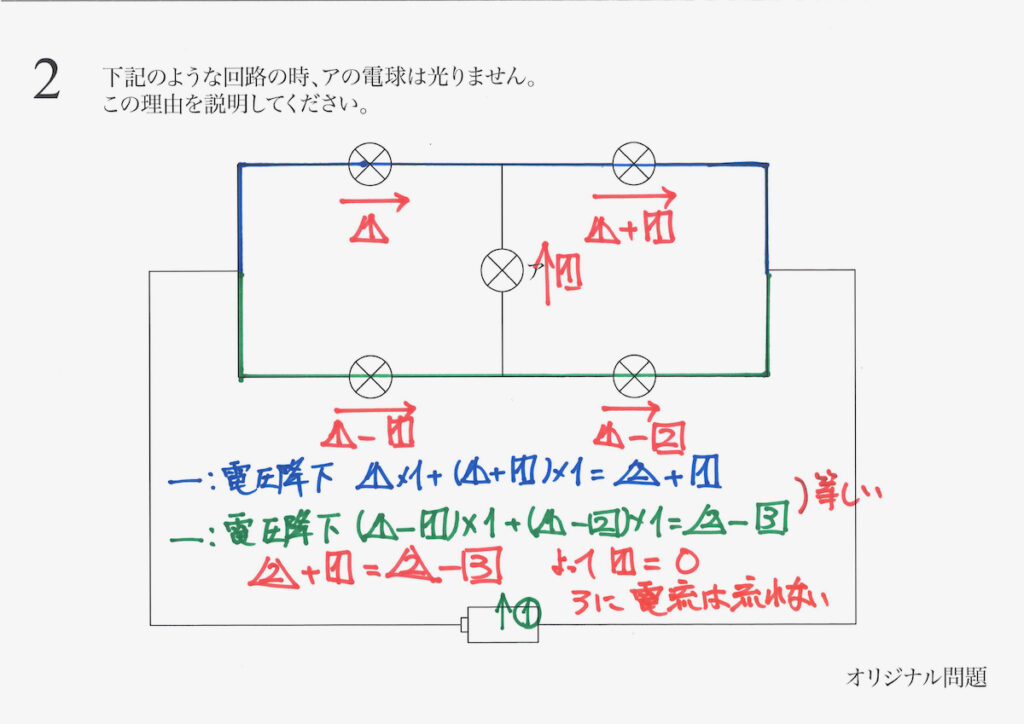
アに流れる電流の大きさは、0となるので、アの電球は光りません。
・計算した結果、アに流れる電流が0だから
今回は、「対称性」という大事な性質を考えずに、ひたすら計算して考えてみました。
男子小学生ちょっと
遠回りな気がする。
女子小学生やっぱり、
対称性に気づいた方が良いわ。
確かに「対称性」に気づくことは大事なことです。
そして、理科では、「対称とするモノ・コトの性質」を理解することが非常に大事です。
この「ひたすら計算して解く」のは、
男子小学生ちょっと、
センスが悪いのかな？
「センスが良くない」と感じるかもしれません。
この考え方は、様々な方の意見があると思います。
筆者は、この様に「性質に気づかなくても、ひたすら計算して答えにたどり着く」力も大事と思います。
それもまた、理科や算数の一つの大事な力だと考えます。
問題文を見て、
男子小学生あっ、
あれだ！
こう分かることも大事ですが、手を動かして進むことも大事です。
色々な考え方を、しっかりと学んで、理解しておきましょう。
理科・算数の学力を上げるためには、特にこのように「しっかりやる」ことが大事です。
すると、総合的に力が伸びて、学力が上がるでしょう。
次回は下記リンクです。
