前回は「学力・成績アップする勉強法〜大事な問題のまとめノート・学力アップが分かりにくい算数・基本的解法・定石をマスター〜」の話でした。
整数問題必勝法：まずは倍数・約数を考える
今回は整数問題必勝法「倍数・約数を押さえる」の話です。
問題6の解法Aの話を、上記リンクでご紹介しました。
この時、大きな要素として「生徒数・学年数・バスの台数」が出てきます。
生徒数は、男子生徒数と女子生徒数に分かれます。
単純に未知数を設定すると、なかなかうまく行かないです。
この「未知数設定」には、「生徒数・学年数・バスの台数は整数」という大事な条件が含まれていません。
ここでは、まず男子：女子=16:15に着目することが大事でした。
「男子生徒数は16の倍数、女子生徒数は15の倍数」になることに気づくことが大事でした。
ここで、男子・女子それぞれ分けて考えても解けます。
15=3×5で、16=2x2x2x2ですから、15も16も比較的「馴染みのある数字」です。
対して、15と16の和の31は、それほど馴染みがある数字ではありません。
31が「馴染みがない」理由は、「31が素数である」からです。
男子・女子を分けて考えても良いですが「大枠=学年全体」を考えてみましょう。
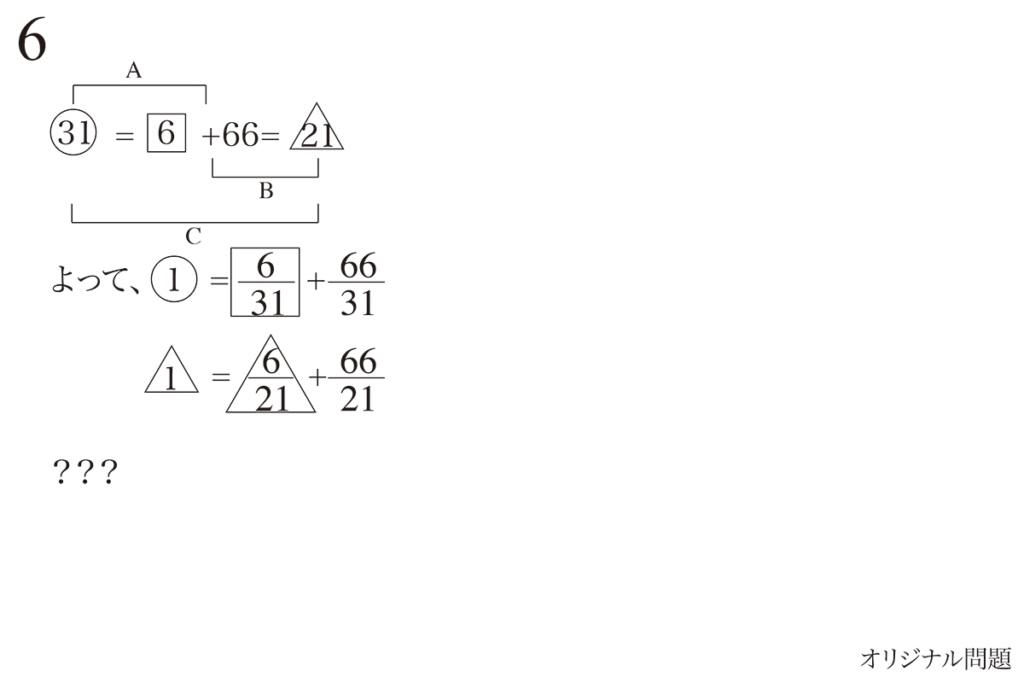
男子：女子=16:15から、「全校生徒数は16+15=31の倍数」となることが、ポイントです。
大きな数字を考える：最小公倍数
全校生徒数は「31の倍数であり、21の倍数である」必要があります。
男子小学生これで、一気に
問題が解ける気がする！
これでかなり絞ることができ、全校生徒数は3パターンになります。
21=3×7ですから、馴染みのある数字です。
仮に先ほどの和=31が3か7の倍数の時、21とその数字に公約数があるので、対象が絞りにくくなります。
今回は、31が素数（約数のない整数）であることがポイントです。
素数は「約数がない」ため、他の数字との最小公倍数が大きくなる傾向があります。
・約数がない数
・素数と他の数の最小公倍数は、比較的大きな数字になる
「素数という馴染みがない数字」が登場することに気づくことが大事です。
全校生徒の人数は6学年であり、「42+24=66」も6の倍数であることがポイントです。
その結果、「全校生徒数は31、21、6の倍数」となるので、一気に対象が絞れました。
文章から具体的にイメージ
この問題では、「各学年の人数」と同時に「学年数」がポイントとなります。
「学年数=6」に気づくことが、一つのポイントになります。
これは問題文に「6学年」とは書いていないので、「気づきにくい」です。
このように「小学校の生徒数」などの身近な問題が出てきたら、具体的にイメージしましょう。
この場合は、「自分が通っている小学校を」イメージしてみましょう。
男子小学生マンションができたら、
地域の家族が増えて・・・
男子小学生子どもも
増えるね・・・
マンションはファミリー向け・単身者向けなど、様々なタイプがあります。
女子小学生子どもが
増えると・・・
「子どもが増える具体的イメージ」を持って考えると、
女子小学生あ、そうか・・・
小学校は6学年だから・・・
「小学校の学年は６であること」に気づきやすいです。
こういう時、
男子小学生う〜ん、
分からない・・・
悩んでしまうことが多いですが、小学校の簡単な絵を描いてイメージすることも大事です。
「小学校の簡単な絵」を描くのは、30秒掛らないで描けそうです。
男子小学生絵を描くのは求められてないから、
時間がもったいない・・・
「時間がかかる」と感じる方もいるかもしれませんが、「描きながら脳は考えている」のです。
そして、「文章だけよりも、具体的な状況を思い浮かべる」と、
女子小学生あっ、この問題のポイントは、
ここかな！
問題のポイント・鍵をつかみやすいです。
整数問題で、いくつかの数字が出てきたら「倍数・約数を考える」ことが大事です。
さらに
男子小学生関係のある
数字はどれかな？
「状況を数値に置き換える」発想が大事です。
男子小学生学校があって、
バスがあって・・・
バスの簡単な絵を描いてみるのも良いでしょう。
「ちゃんとしたバス」を書く時間がかかるようでしたら、単純な長方形でも良いでしょう。
描いているうちに、
男子小学生あっ、
6学年だ！
「問題のポイント」に気づく可能性が高まります。
算数でも理科でも「イメージしてみる」「簡単な絵を描いてみる」は、非常に大事なことです。
「イメージ」によって、文章題はかなり考えやすくなり、解きやすくなるでしょう。
次回は下記リンクです。
