前回は「てこのつり合いのコツ・考え方 4〜つり合う時とつり合わない時・てこの原理のイメージ・「てこ」と加藤清正の熊本城・「なぜだろう？」と考える姿勢・モーメントと「回転する力」〜｜中学受験・理科」の話でした。
てことモーメント（回転する力）のイメージ
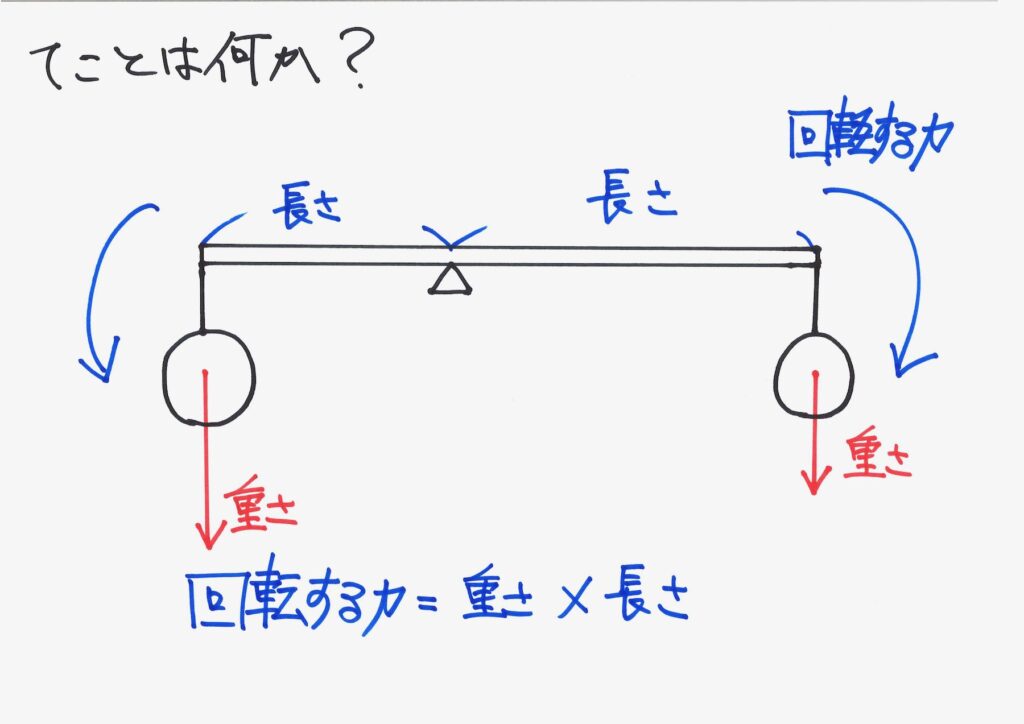
バネ、かっ車などでは登場しなかった「モーメント（回転する力）」が登場する「てこの問題」。
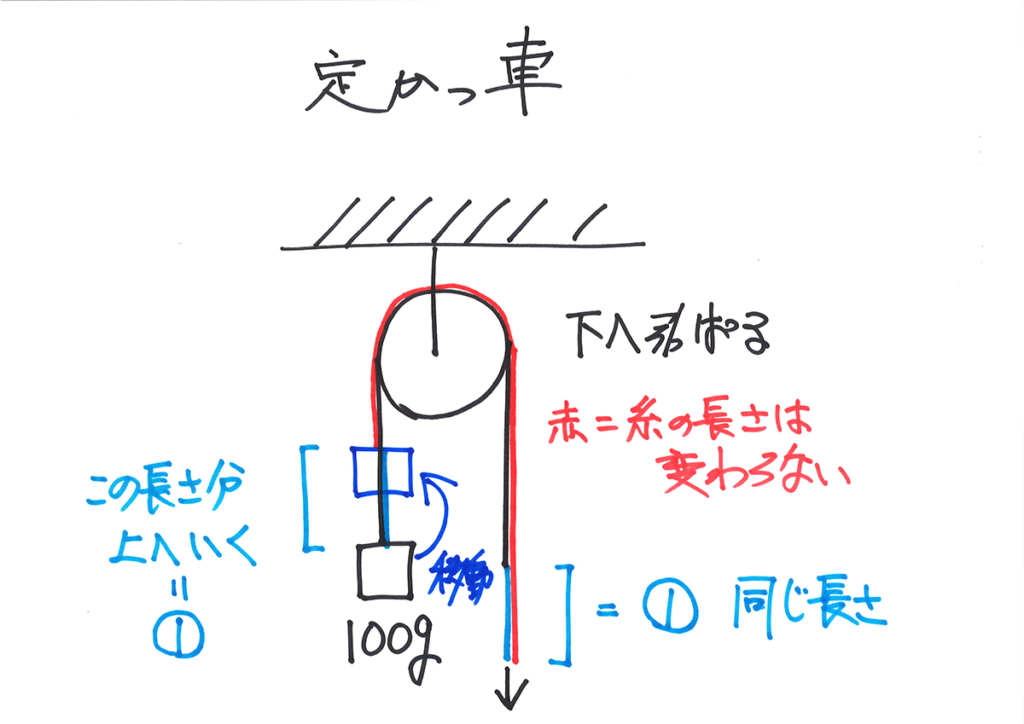
バネ、かっ車では、「重さ・力の矢印」を描いて考えれば、解けます。
男子小学生なぜ、てこでは
モーメントが出てくるんだろう？
女子小学生確かにそう・・・
力・重さだけでは出来ないの？
・モーメントは「回転する力」
・「力 x 長さ」でグルッと、何かを回転させるイメージ
「モーメント」と言うと、少し難しい感じかも知れません。
「力 x 長さ」でグルッと回転させるイメージを持ちましょう。
バネ、かっ車などでは登場しないモーメントは、「モーメントが存在しない」ではないのです。
実際には、全てのモノの動きには、力・重さとモーメントがあります。
建物の構造設計でも、重さ（重力）とモーメントが大事です。
・力（重力）、重さなどのつり合い
・モーメント（回転する力）のつり合い
大きな建物でも、みなさんが座っている椅子でも、力・重さとモーメントの両方がつり合っています。
そこで、「モーメントが登場する」てこを「かっ車・バネと別」と考えないようにしましょう。
そして、モーメント（回転する力）を難しく思わないようにしましょう。
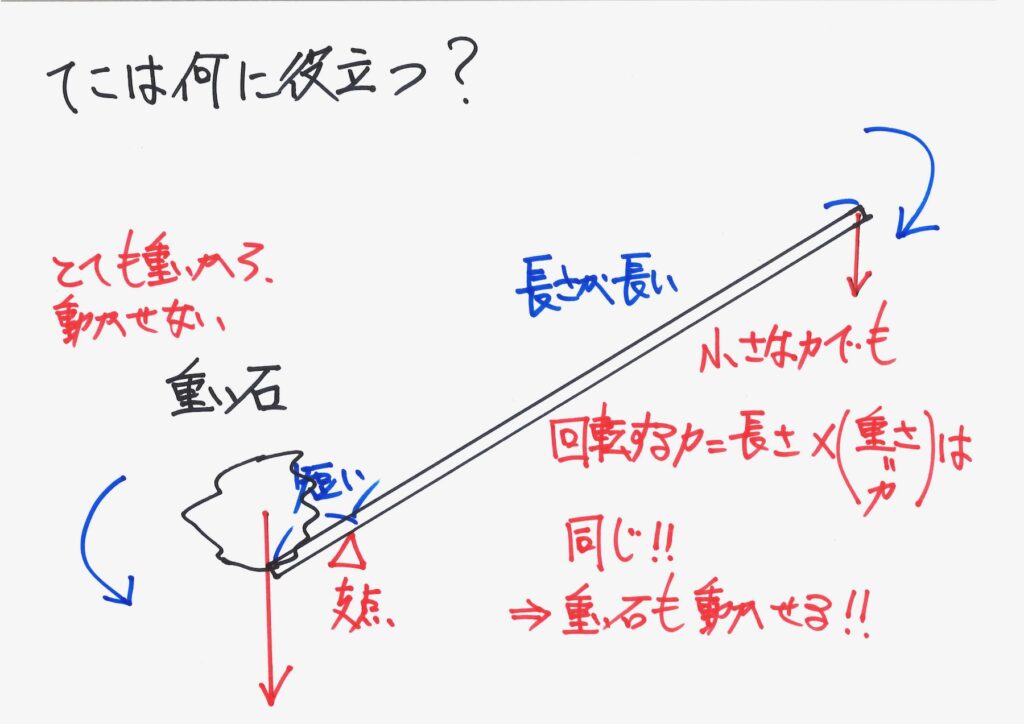
実際に、実生活で上のように「てこを使う」ことは、少ないかも知れません。
その意味では、電車・自動車などにあるバネ・電気とは、少し縁遠い存在かも知れない、てこ。
原理的には、「長さを調整すれば小さな力で、すごく重いモノを動かせる」のです。
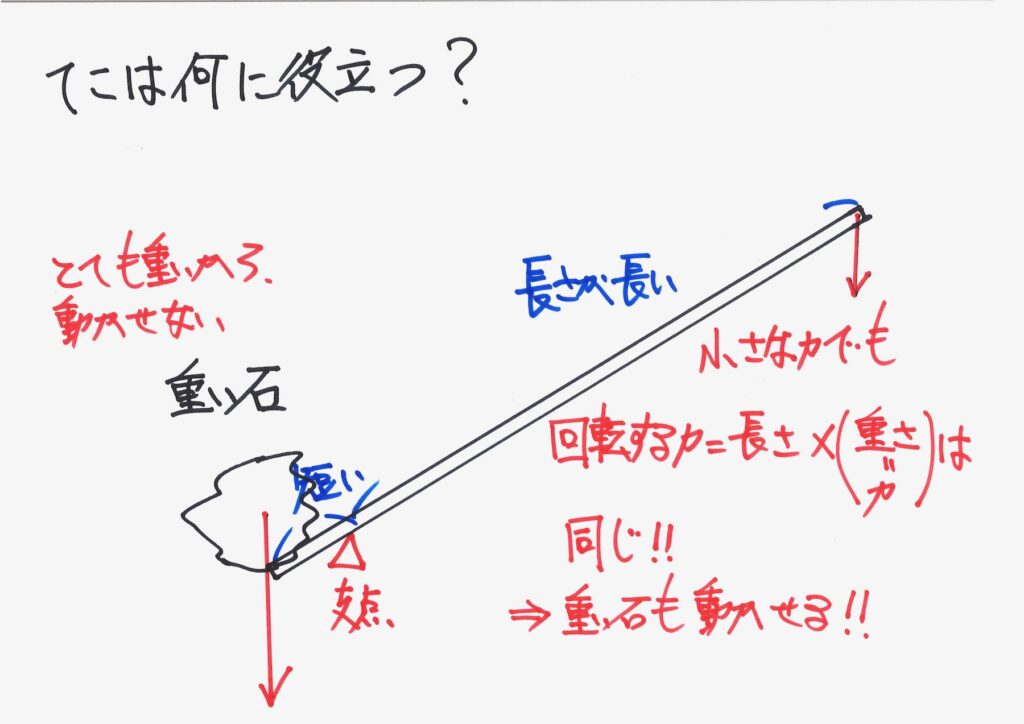
小学生の力でも、「重い・巨大な石を動かせるかも知れない」のです。
男子小学生確かに
そうだね・・・
女子小学生確かに
ちょっと面白いかも・・・
このように、理科は「面白いこと」を考えると良いでしょう。
男子小学生この分野を
勉強して、出来るようにならなきゃ！
「とにかく勉強」になりがちな受験勉強。
理科などでは、実際に役立つイメージなどを考えると、理解が進むでしょう。
そして、てこでは「回転する力」を描いて、しっかりイメージすることが大事です。
公式を理解する姿勢：「逆比」の説明
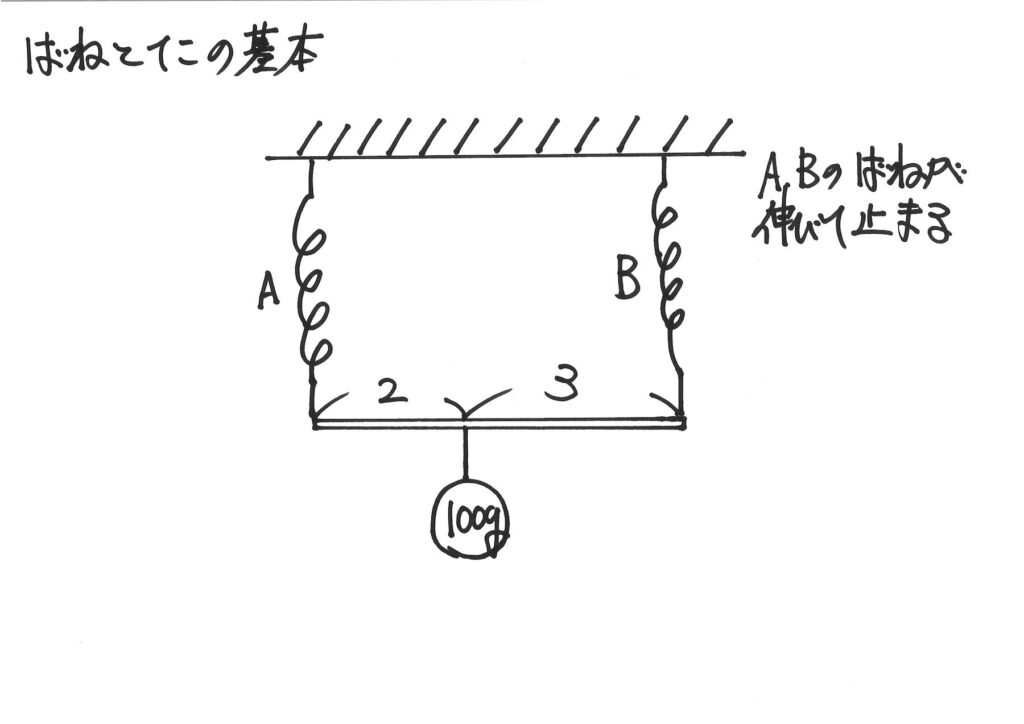
今回は上の表な状況を考えましょう。
今回は「棒の重さは考えない」とします。
男子小学生これは、
分かるよ！
男子小学生バネA、Bには、2:3の逆比の、
3:2の重さが掛かるんだよね。
女子小学生「バネの基本の解き方」として、
教わった！
この「長さの逆比の重さ・力」あるいは「重さ・力の逆比の長さ」は、公式になっています。
この「なぜ逆比か？」を説明できるか、考えてみましょう。
男子小学生えっ、
説明？
男子小学生「そういうものだ」と
思っていたよ。
女子小学生そう・・・
「なぜ？」ではなく、そこから始まると思っていた・・・
女子小学生似た問題も、このように「逆比」で考えれば
解ける、って習ったけど・・・
「なぜか？」をしっかり理解すると、理科・算数は一気に学力が上がります。
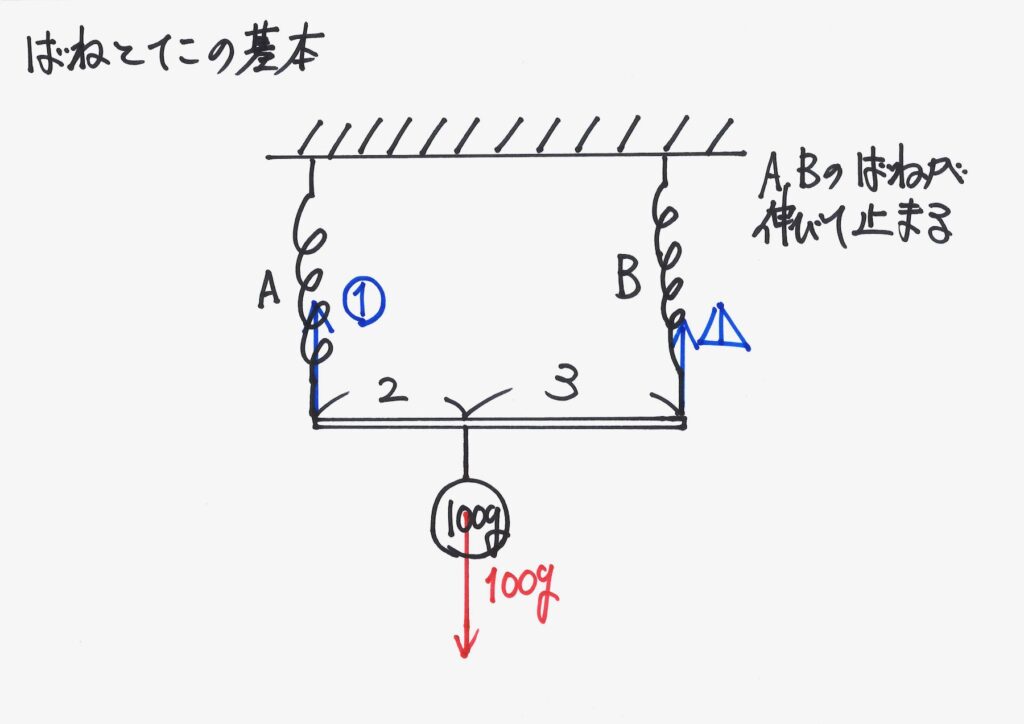
この問題で、「逆比が・・・」と考える前に、「バネが伸びて止まる」ことを考えます。
100gの重さを「2本のバネで支えている」イメージです。
引っ張られるイメージが強いバネですが、実際には「伸びて、引っ張り上げている」のです。
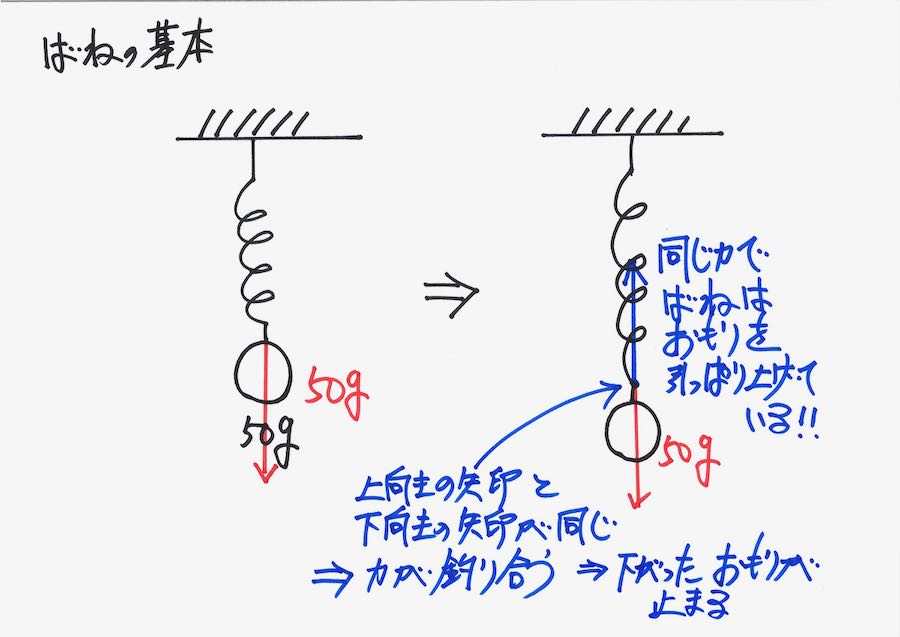
バネの問題の図を見ると、「バネにおもりがかかって、動きがない」ような気がします。
実際には、バネは「伸びて、重さ・力を引っ張り上げている」ことをイメージしましょう。
実際に、バネをグルグルっと描いて「伸びた状況」を描くと分かりやすいでしょう。
ここで、先ほどの公式：逆比で、これらが分かります。
「分からない」として、それぞれの力を未知数で設定します。
男子小学生えっ、
分からないの？
男子小学生ここから、
どうするの？
基本的な考え方がしっかりしていれば分かるので、やってみましょう。
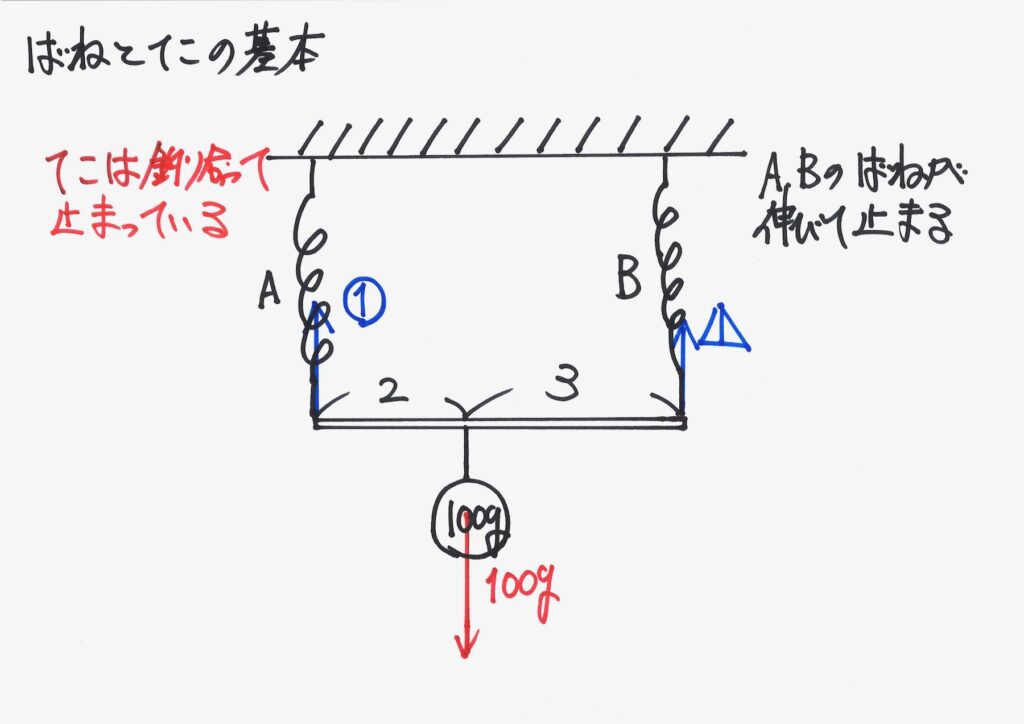
てこは、つり合って止まっている（静止）しています。
この時、てこの棒も「つり合って水平」になっています。
そして、「バネが伸びて、止まっている」状況を考えましょう。
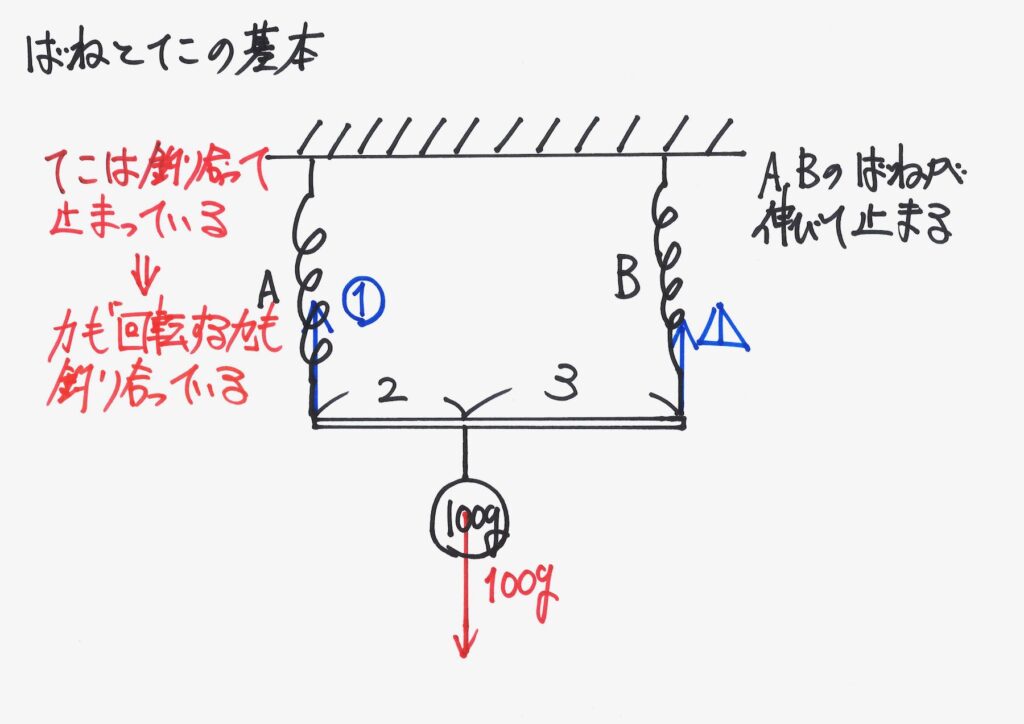
「釣り合っている」のは、特殊な状況です。
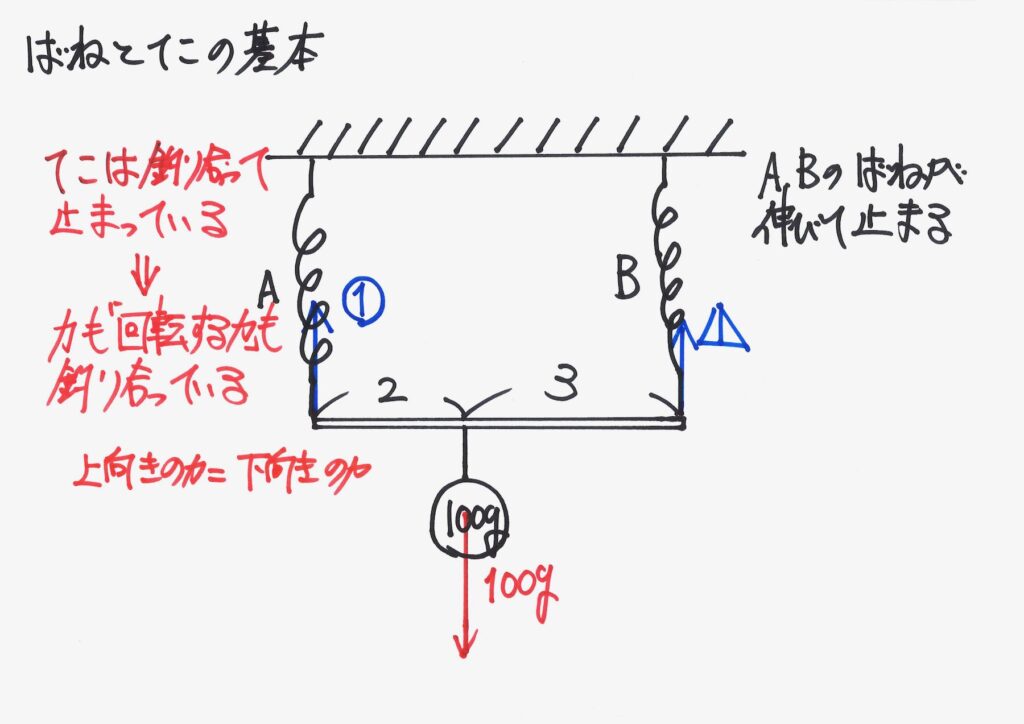
この状況は、まず「上向きの力と下向きの力が釣り合っている」ことが大事です。
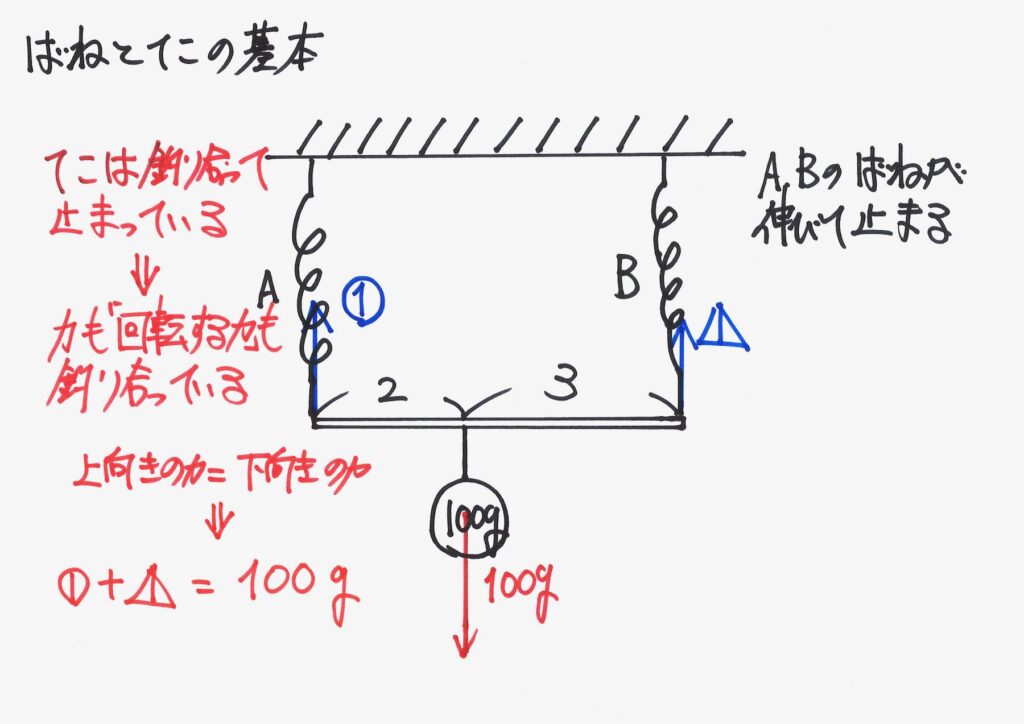
不明な「2本のバネが引っ張っている力」の合計は、分かりました。
男子小学生これは、
分かるけど・・・
男子小学生ここから、
どうするの？
「釣り合っている」状況の、もう一つ大事なことがあります。
女子小学生「モーメント=回転する力」が
釣り合っている、ことだね！
回転する力を、考えてみましょう。
女子小学生でも、どこを支点に、
考えれば良いのかな・・・
男子小学生そう、
支点がないから、「つり合い」が分からないよ・・・
「つり合っている」=特殊な状況：支点を考える
本来「つり合っている」のは、特殊な状況です。
このようにバネ・おもり・棒を使って、実際にやってみると良いでしょう。
小学校で上皿てんびんを使って、重さを測ったことがあると思います。
男子小学生釣り合わせるのって、
結構大変だよね・・・
女子小学生少しずつ「おもり」を
乗せてゆくのが大事だね。
バネ・おもり・棒の全てを家庭で揃えるのは、結構大変なので、学校で実験すると良いです。
このような「バネ・おもり・棒のつり合い」の実験を実際にやる機会は少なそうです。
何かの教材等で「バネ・おもり・棒のつり合い」が、あれば良いです。
実際にやってみれば分かりますが、問題文のように「棒が水平になるように」は難しいです。
少しおもりの位置がずれていると、「棒は傾いてしまう」はずです。
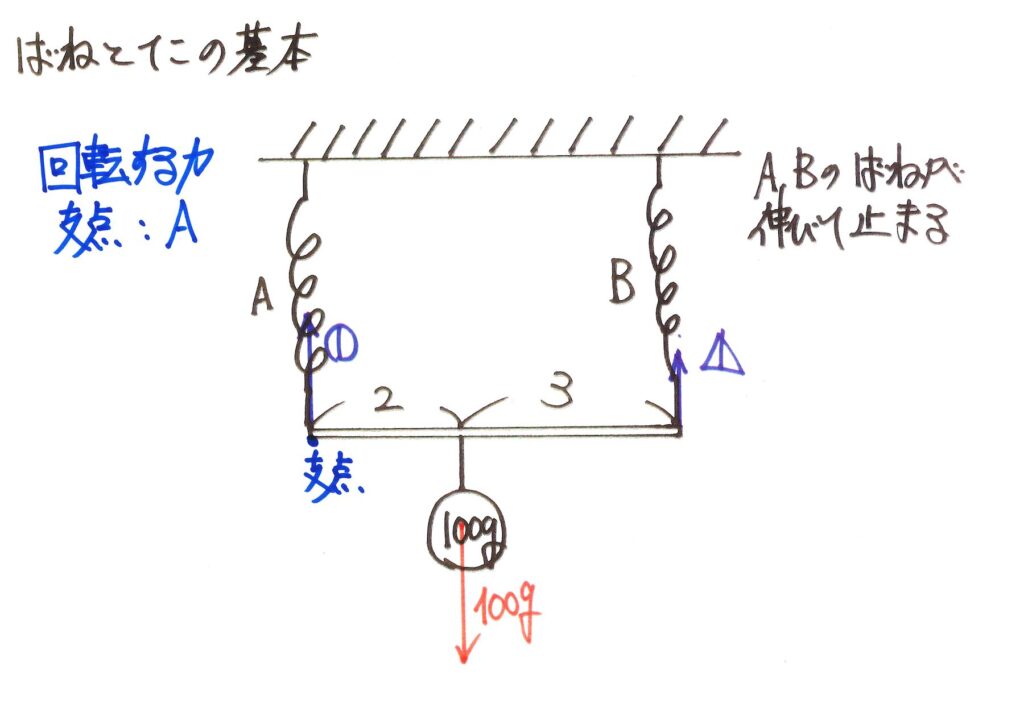
「釣り合っている」ことを、もう少し考えてみましょう。
例えば、Aのバネと棒の繋がっている点（接点）は、釣り合っていて、動きません。
この点を中心にして「回転する力」を考えると、「釣り合っていなければならない」のです。
女子小学生確かに
そうだね。
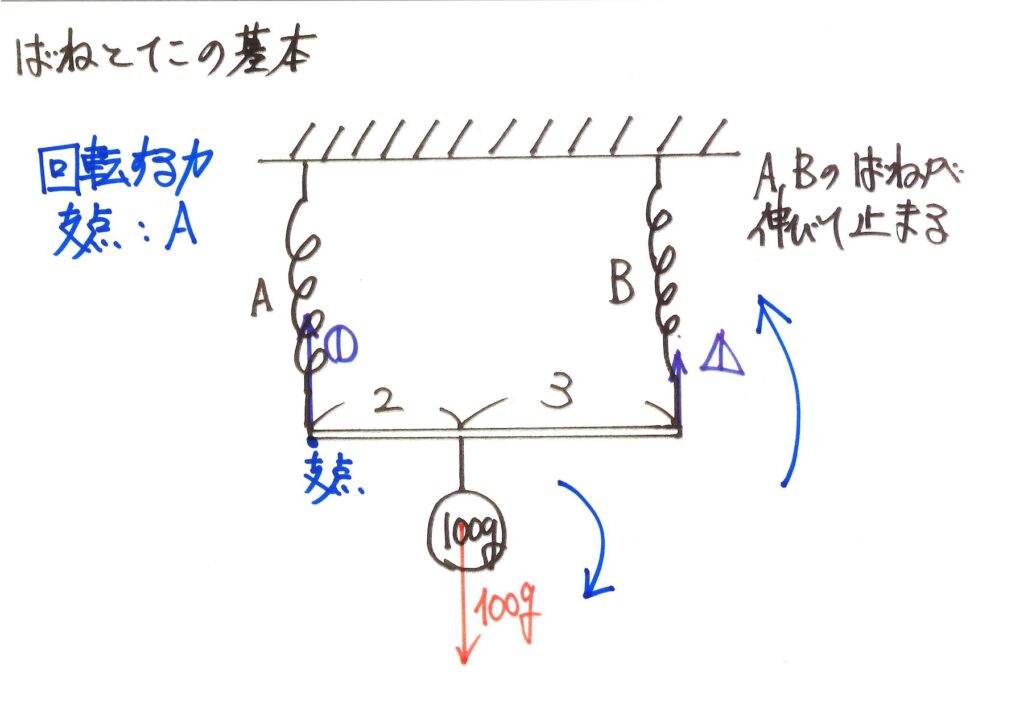
Aのバネと棒の繋がっている点を中心に、「回転する力」を描きましょう。
おもりが「時計回りに回転する力」を、バネBが「反時計回りに回転する力」を作ります。
男子小学生これは分かるけど、
ここは支点ではないけど・・・
支点とは文字通り「支える点」です。
・棒などのモノを支える点
ここが支点であれば、ここで「重さの一部を支えている」状況になります。
その状況ではないですが、この点で「つり合っていないと、動いてしまう」イメージを持ちましょう。
男子小学生確かに、
つり合ってないと、動くかも・・・
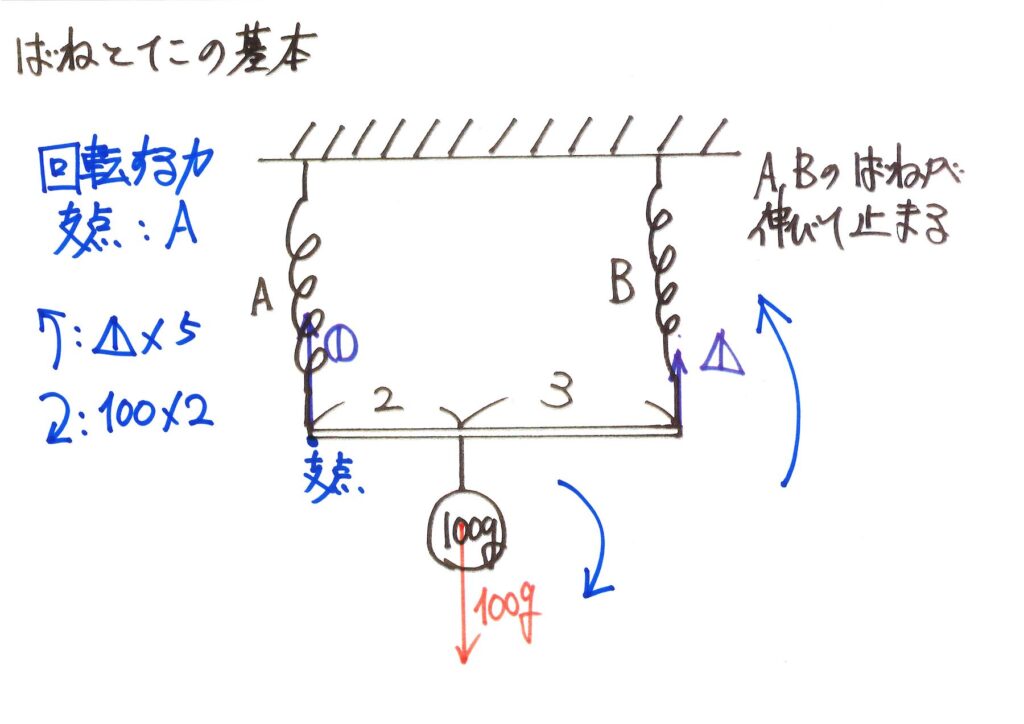
簡単にグルッと「回転する矢印」で、それぞれを表現しましょう。
このようにグルッとモーメント（回転する力）を描くと、この状況が分かりやすいでしょう。
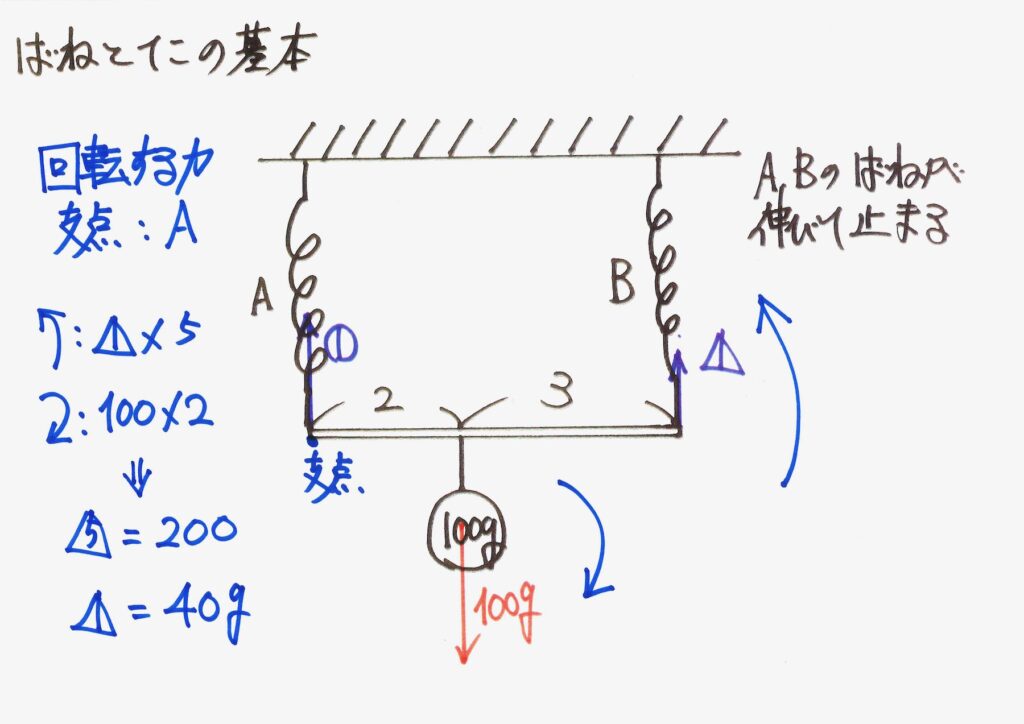
これら二つの「回転する力」が等しいので、バネBの引っ張る力が分かります。
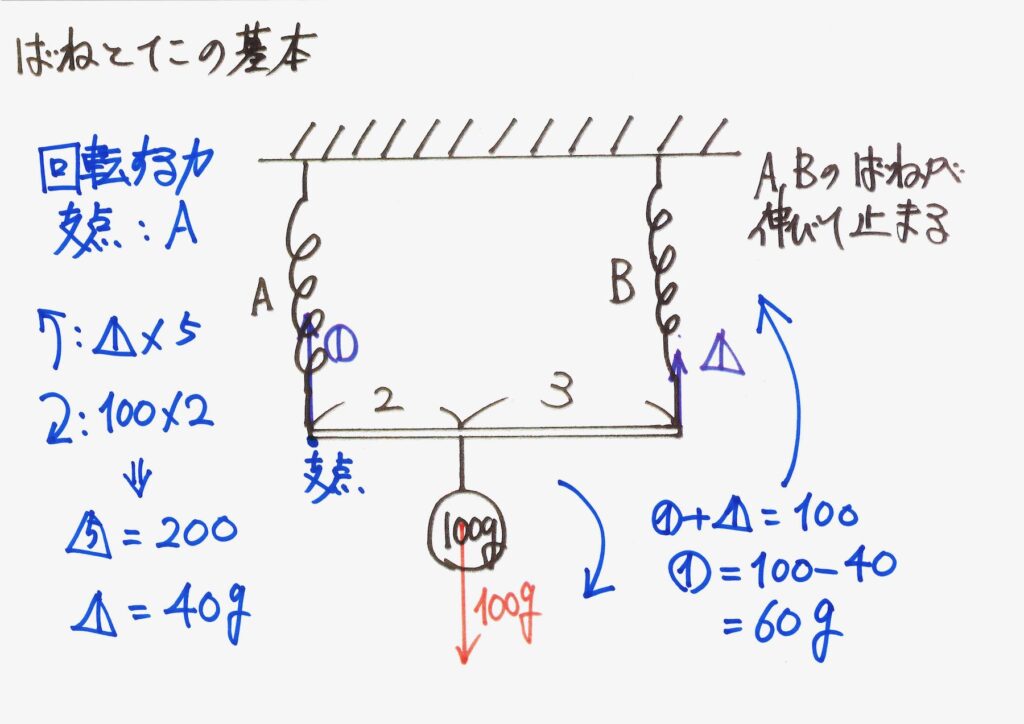
「バネA,Bの引っ張る力の合計」は、おもりの重さと同じなので、バネAの引っ張る力も求まります。
女子小学生これで、
スッキリ分かった！
男子小学生「回転する力」を考えると、
よく分かるね！
それでは、バネBと棒の繋がっている点を中心に、「回転する力」を考えてみましょう。
この点も「つり合って、動かない」状況です。
次回は下記リンクです。
