前回は「動く図形の面積を予想して考えるポイント〜状況を予想する大事さ・描いてイメージ・対象を評価・増える面積と減る面積を比較・具体的に大小を比較・問題 11(5)解法A〜」の話でした。
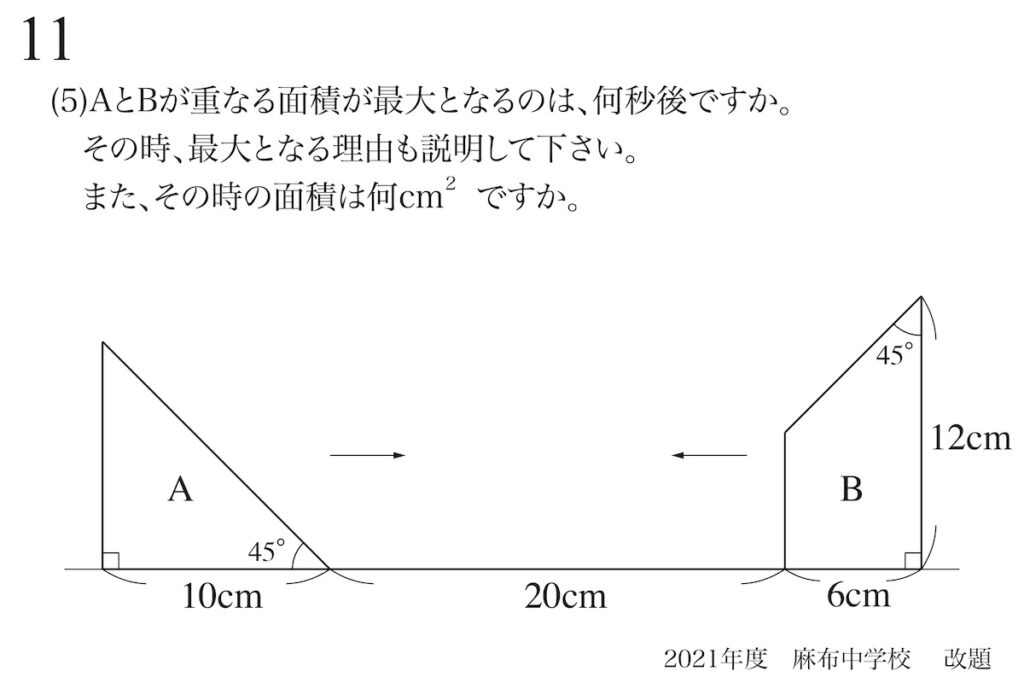
問題11(5)（再掲載）
未知数への姿勢：ケーキやピザをイメージ
直角二等辺三角形と台形が重なる部分の「面積が最大となる」時を予想して、考えました。
・あるものの大小を比較：大きいと小さいを意識
・「大きい」と予想した対象は「より大きく」そして「小さい」と予想した対象は「より小さく」
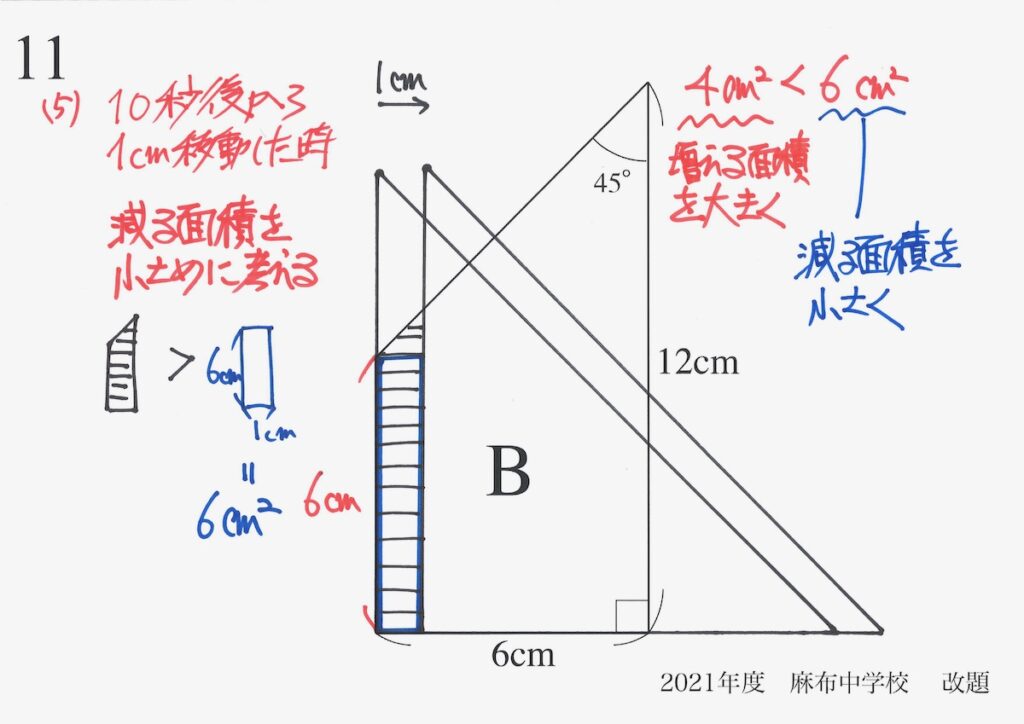
具体的に「増える面積」と「減る面積」の両方の面積を直接計算せずに、簡単な面積で評価しました。
その結果、「増える面積 < 減る面積」が分かりました。
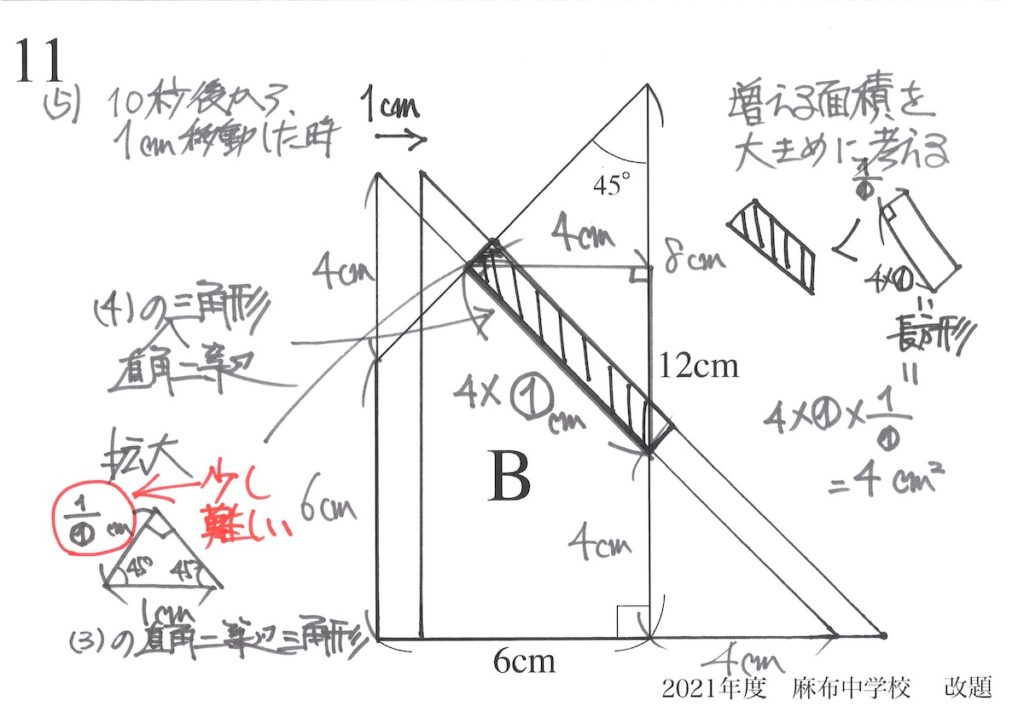
ところが、少し難しい「分からない数①で割る」が出てきました。
「①を掛ける」のは、箱とかを
イメージすれば、なんとなく分かるよ。
分からない数で「割る」のは、
どんなふうにイメージすれば良いのかな・・・
「四則演算の範囲」ですが、「分からない数①を掛ける」に比べて、少し分かりにくいです。
ケーキやピザなどを「分割する」などでイメージするのが一つの手法です。
①などが2とか3ならば、「分割するイメージ」が頭に思い浮かべられると思います。
でも、今回は「①x①=2」っていう
分からない数字だから・・・
分からない数字を
イメージするのは無理だよ・・・
少し分かりにくいかもしれません。
「分からない数字」も「分かりやすい数字と同じように考える」と割り切るのも一つの手段です。
数学だと、こういう計算は「機械的にする」傾向があります。
算数なので、イメージすることを大事にしましょう。
少し分かりにくいので、もう少し違う角度から考えてみましょう。
もっと大雑把に考える：分かる長さを考える
長方形の面積を考えていますが、「短辺の長さが分からない」としましょう。
ここでは、「1/①」と分かるのですが「分かりにくい」ので、違う比較の仕方を考えましょう。
「大小を比較」しているので、「三角形の斜辺の長さは、二つの辺より長い」を考えましょう。
うん。
それは分かるよ！
これは分かるけど、
「1cmより短い」で大丈夫かな・・・
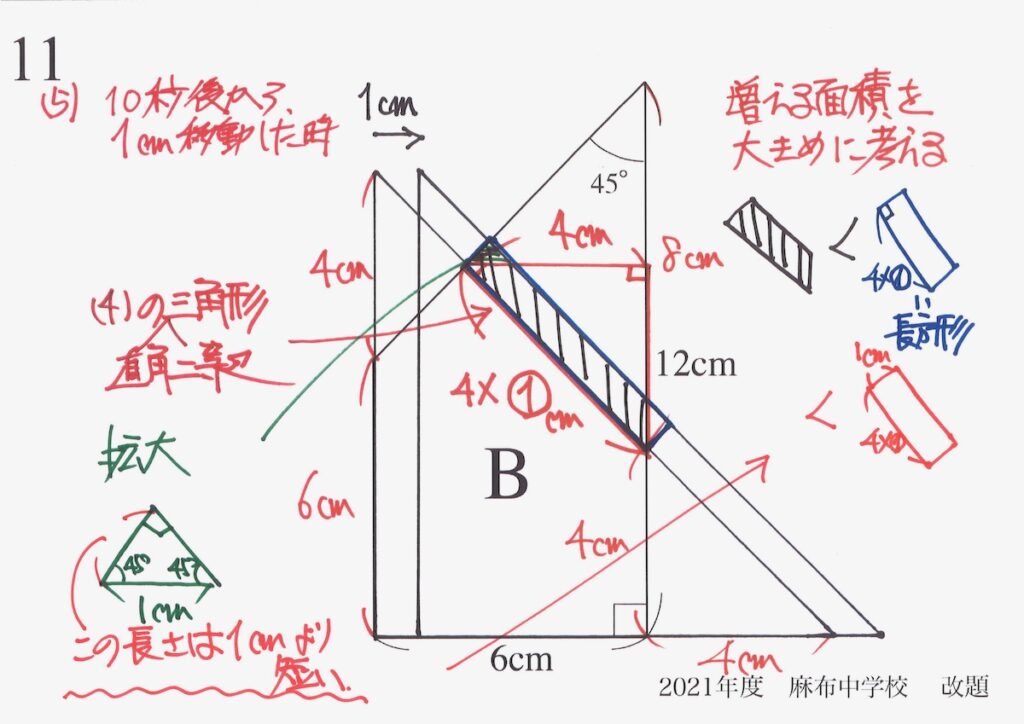
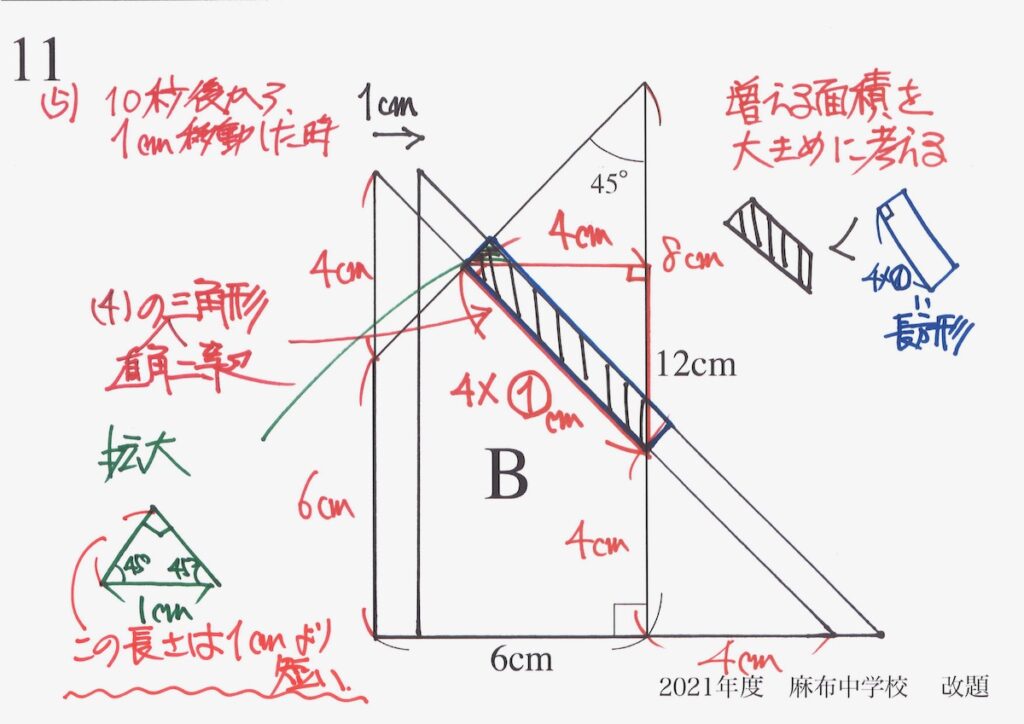
緑の直角二等辺三角形の同じに辺の長さは「斜辺の1cmより短い」ので、右上のように比較できます。
「増える面積 < 4x①」が分かりました。
これで
比較できるの？
ここで、「小問は前の問題がヒントになっていることが多い」を思い出しましょう。
1.最後の問題のみだと難しいため、ヒントを作って解きやすくする
2.問題を分け、出来る部分を明確にして、採点の際に点数の差が出やすくする
この数は、
さっき比較した！
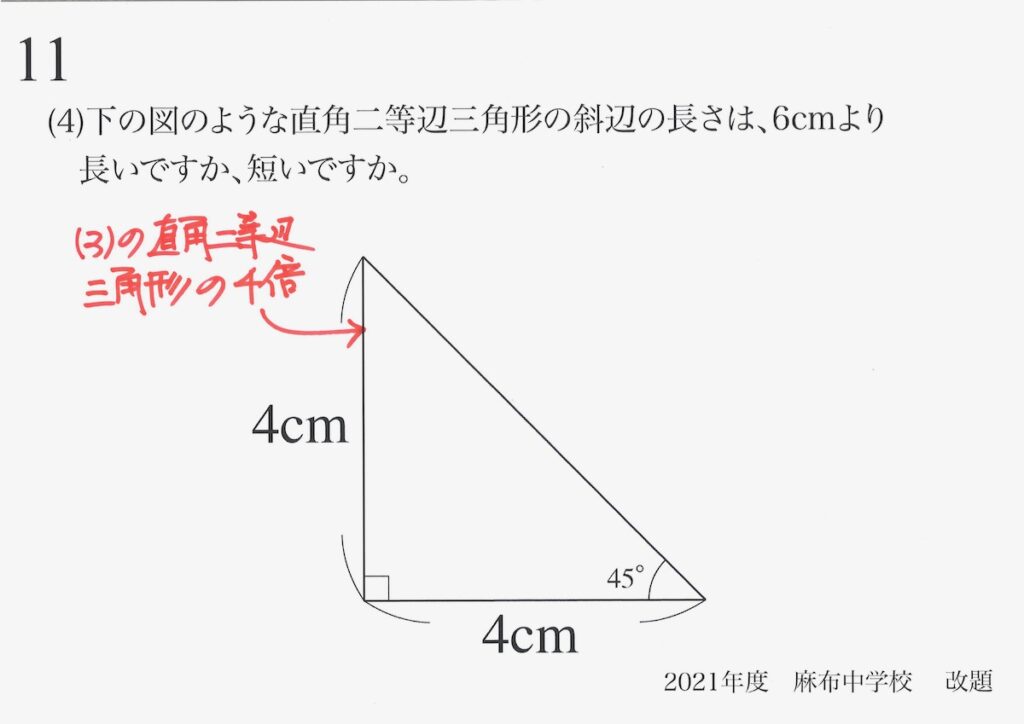
ここで、(4)で考えた直角二等辺三角形と「全く同じ直角二等辺三角形」が登場しました。
確かにそうだね！
たまたまかなあ・・・
こういう時は「たまたま」ではなく、「出題者が考えて、ヒントにしている」ことが多いです。
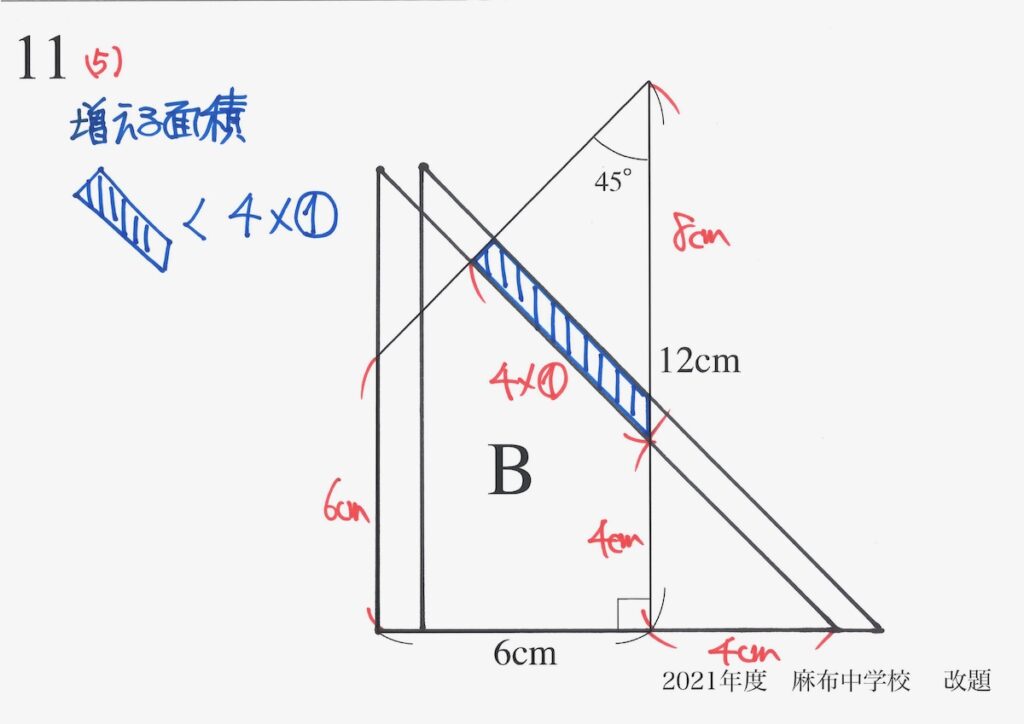
先ほどと同様に「増える面積を大きく、減る面積を小さく」で比較しましょう。
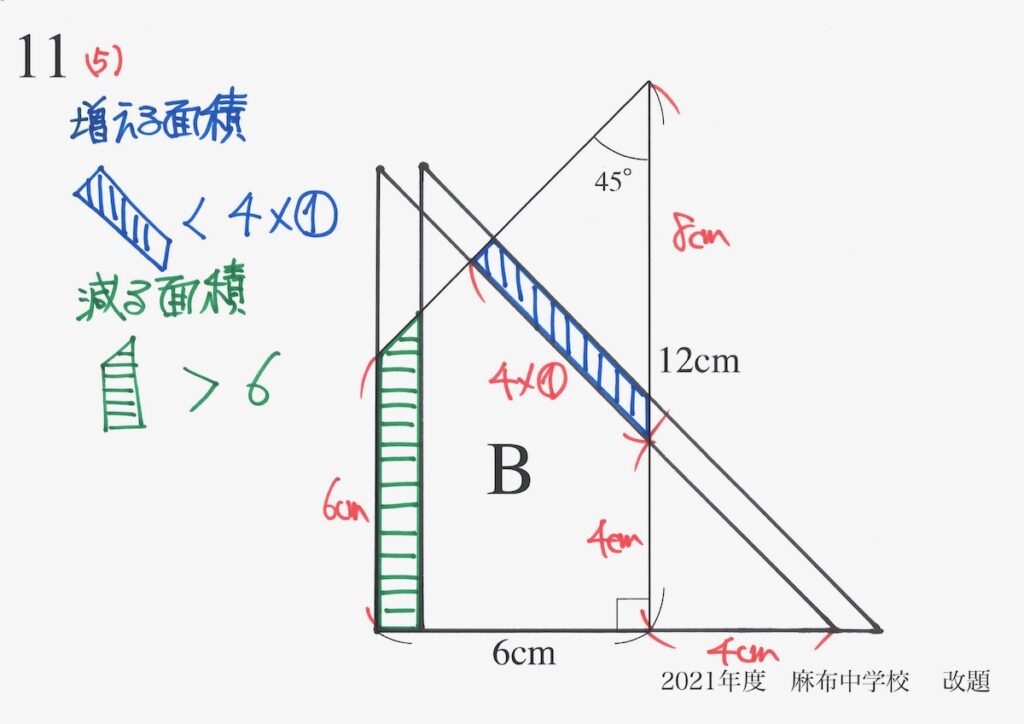
間に挟む面積が
大事なんだよね！
具体的に大小関係を考えてみましょう。
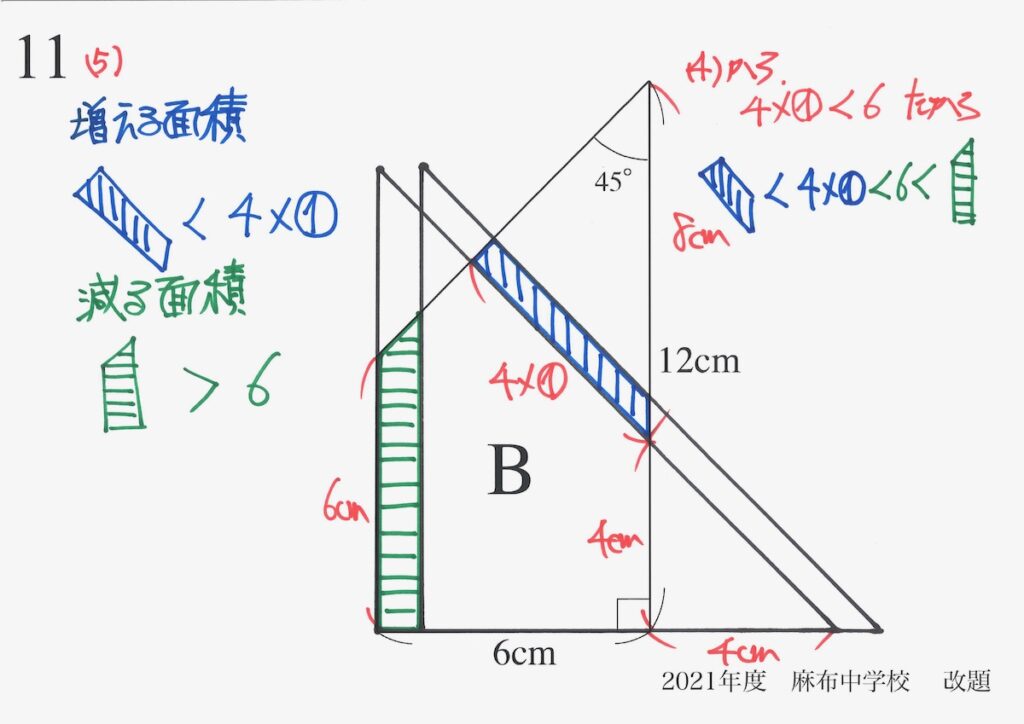
これで
分かったね！
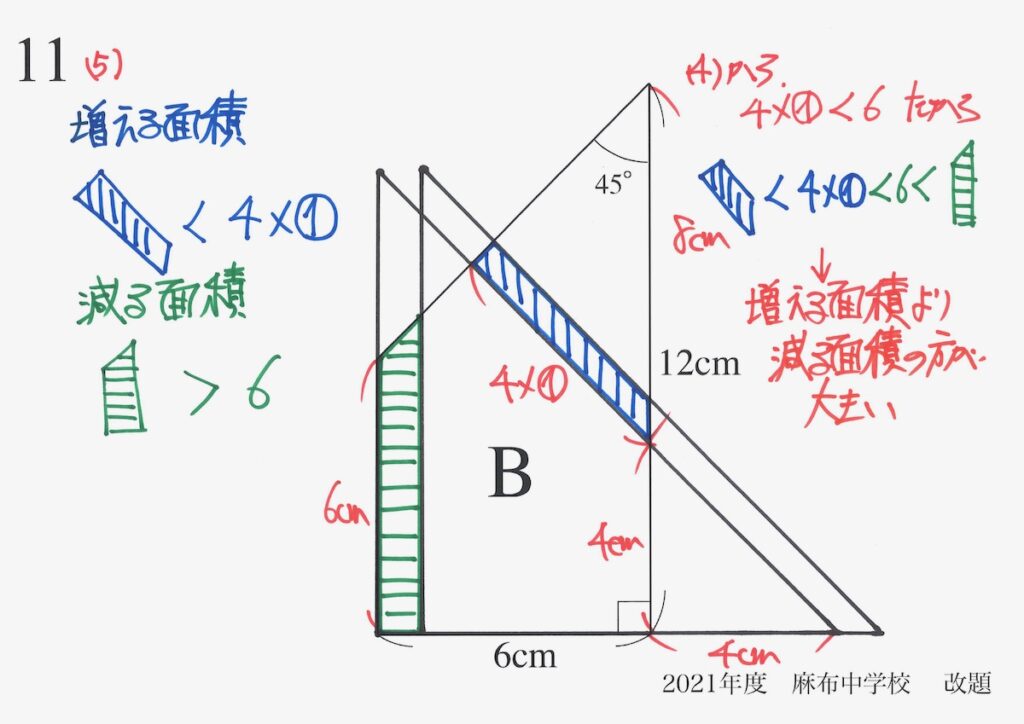
これで「増える面積 < 減る面積」が分かりました。
もっと大雑把に
考えても分かったね！
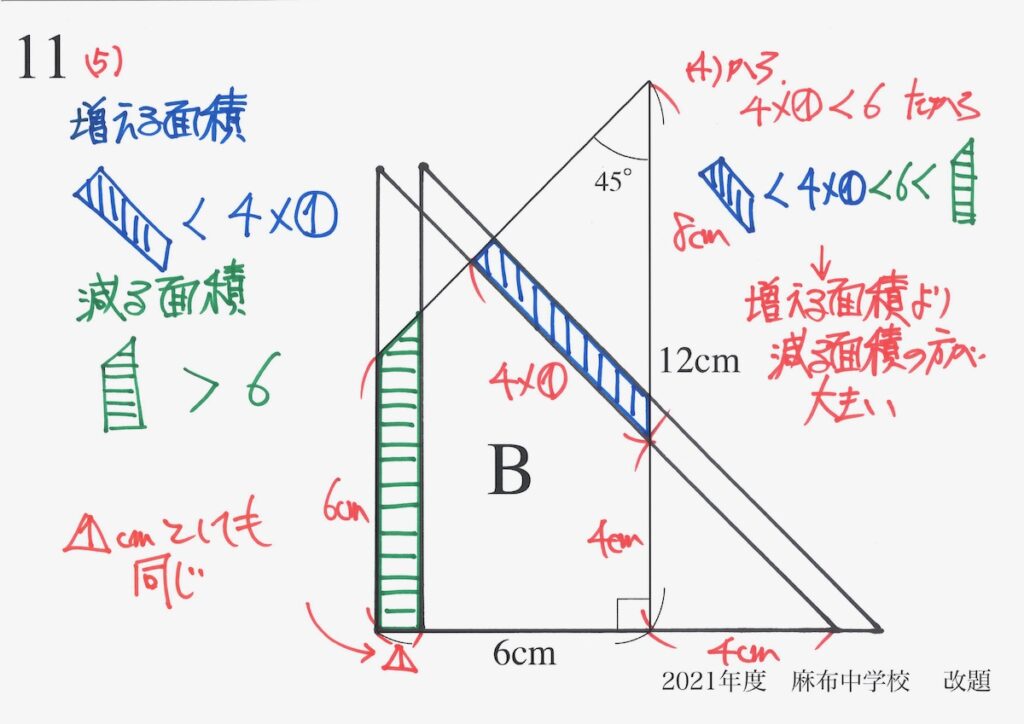
この場合だと、「1cmではなく、他の数字でも同じ」がイメージしやすいです。
これだったら、
「1秒後」でなくても、いつも同じって分かる！
ここから最大値を求めるのは、前回と同様です。
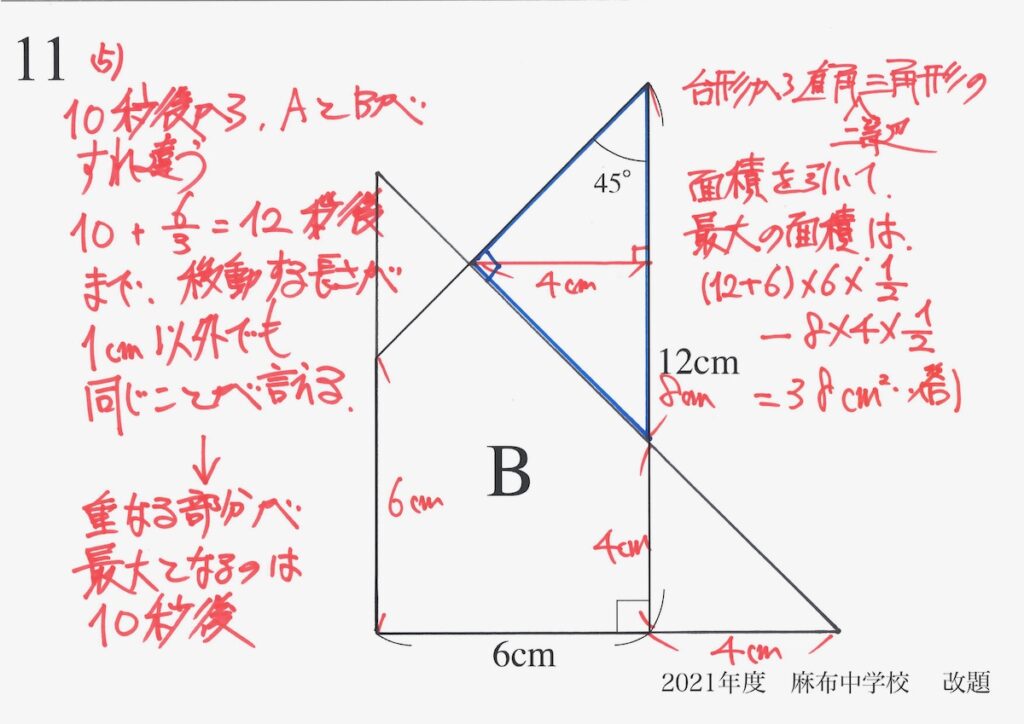
(4)は、
そういうことだったんだ。
小問がある時は、
次のヒントに
なっているかな？
と、考えてみましょう。
すると、より全体像が見えてくるでしょう。
