前回は「動く図形の面積を簡単に考えるコツ〜比較する図形を簡単にする・台形と長方形・減る面積を簡単な図形と比較・問題 11(5)解法〜」の話でした。
問題11(5)(再掲載)
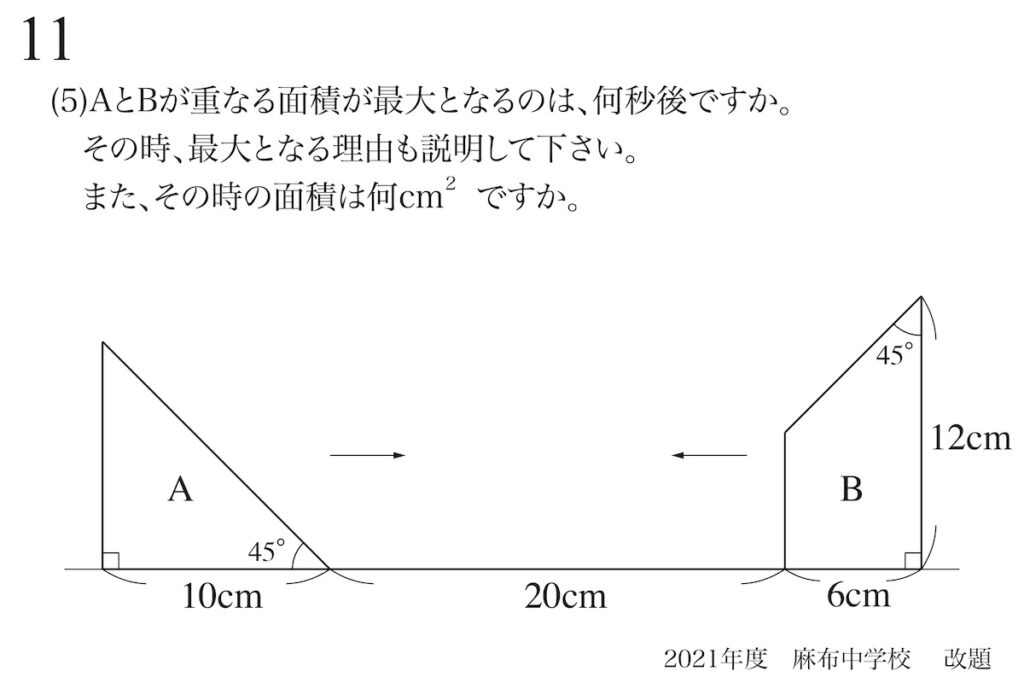
状況を予想する大事さ:描いてイメージ
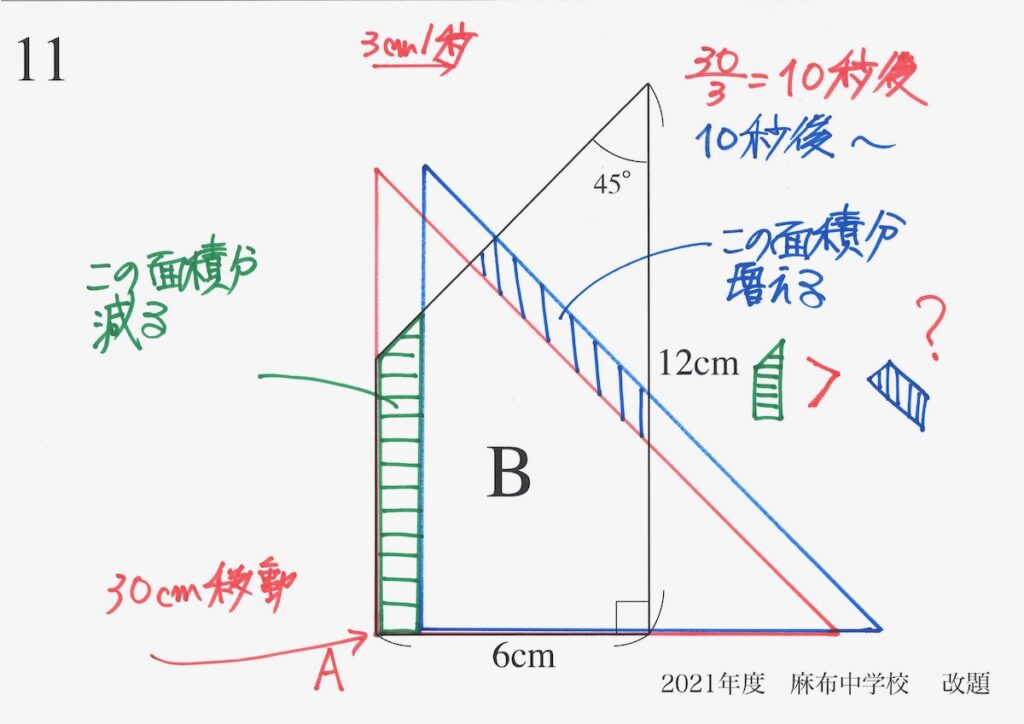
直角二等辺三角形と台形が重なる部分の面積が「最大となる」時は、上の時と「予想」出来ました。
ただし、これは「なんとなく」の予想なので、この理由を説明する必要があります。
中学以降の数学では、最大・最小は「方程式で立式して計算」することがほとんどです。
「方程式で立式・計算」の場合も、「状況を予想する」ことは大事な姿勢です。
算数・数学に限らず、物理・化学分野の理科でも大事なことです。
実験問題などでも「予想する」ことは大事な力で、今回は図形問題に関して考えます。
・動く点や図形に対して状況を予想する
・状況を理解して予想するためには「描いてイメージ」
動く図形の面積を予想して考えるポイント:対象を評価
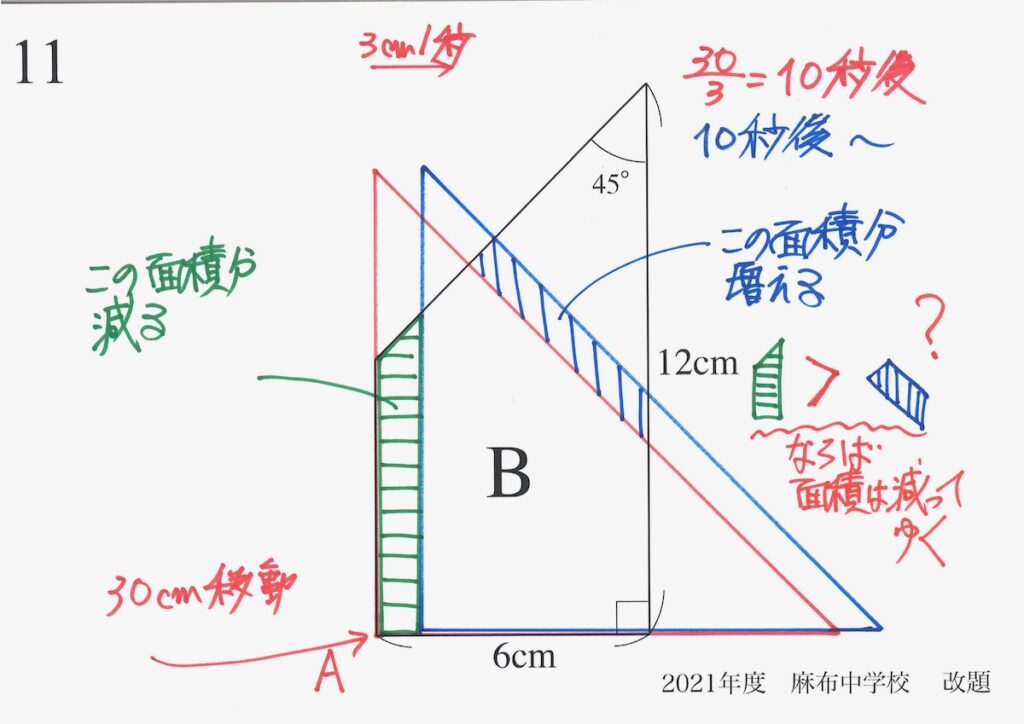
「重なる面積が最大」となる状況を予想して、具体的に「増える面積」と「減る面積」を考えました。
「増える面積」と「減る面積」は、ともに台形で面積を求めるのは難しくありません。
ところが、「台形の辺の長さ」が難しいので、「大雑把に考える」を試みました。
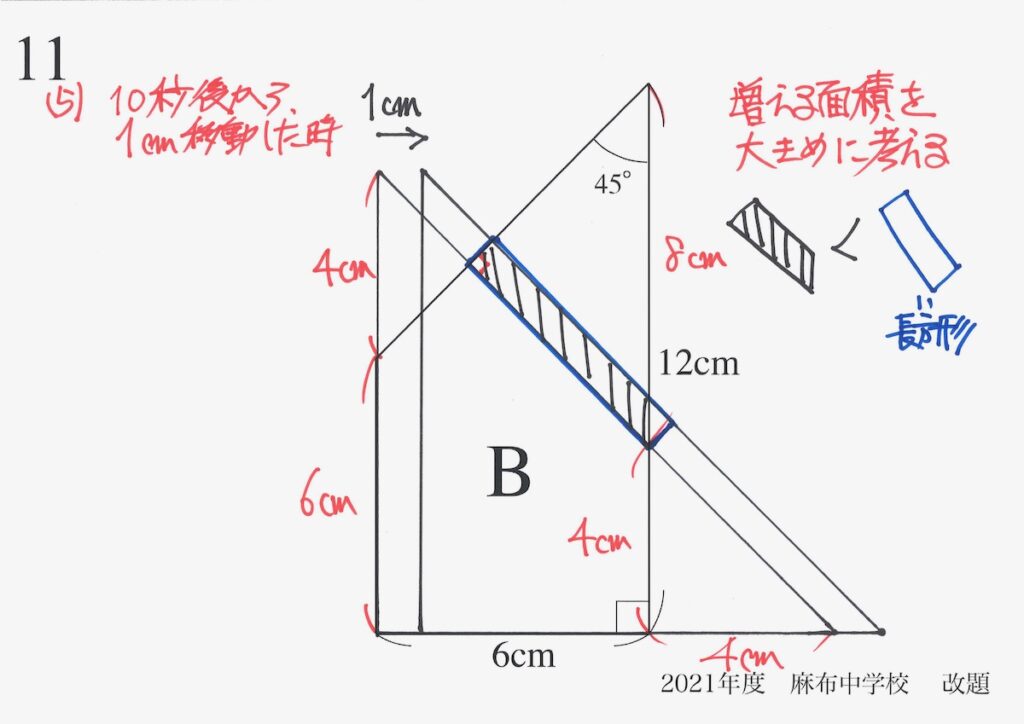
「増える面積」を、少し大きめにして「面積の計算が簡単な長方形」と比較しました。
この「少し大きくする」や「少し小さくする」は、「対象を評価する」ことです。
 男子小学生
男子小学生「対象を評価」って
難しいけど・・・
「評価」は数学的な発想ですが、実は受験生の皆さんは「日頃評価されている」のです。
例えば、



あなたの偏差値は
63です。
偏差値という数字を受けたり、



あなたのA中学の合格判定は
80%以上です。
合格判定を受けることは「評価を受けている」ことです。
他には、小学校の通信簿などがありますが、いずれも「評価されている」ことです。



確かに私たちって、
いつも「評価されている」ね・・・
大人や社会人も大変ですが、学生時代は「常に評価されている」のです。
そこで、たまには「評価する」側に回ってみましょう。



うん!
「評価してみる」をやってみたいね!



でも図形を「大雑把に評価」という
のは、どうやって「大雑把」に評価するの?
ここで「どのように大雑把に評価するか」は、ちょっとしたポイント・コツがあります。
ここで、「大雑把とは?」を考えましょう。
先ほどの、偏差値と合格判定を考えます。
・偏差値63
・合格判定80%以上
ここでは、どちらが「評価が細かい」でしょうか。



それは、1刻みの
偏差値だね!
・偏差値63:1刻みで細かい←こちらは少し細かい
・合格判定80%以上:判定は5種類くらい←こちらは少し大雑把



確かに合格判定って、
少し大雑把なところがあるかも・・・
日頃受けている「自分の評価」にも、「細かい評価」と「大雑把な評価」があるのです。
このように考えて、図形などを「大体の状況を考える」を続けましょう。
増える面積と減る面積を比較
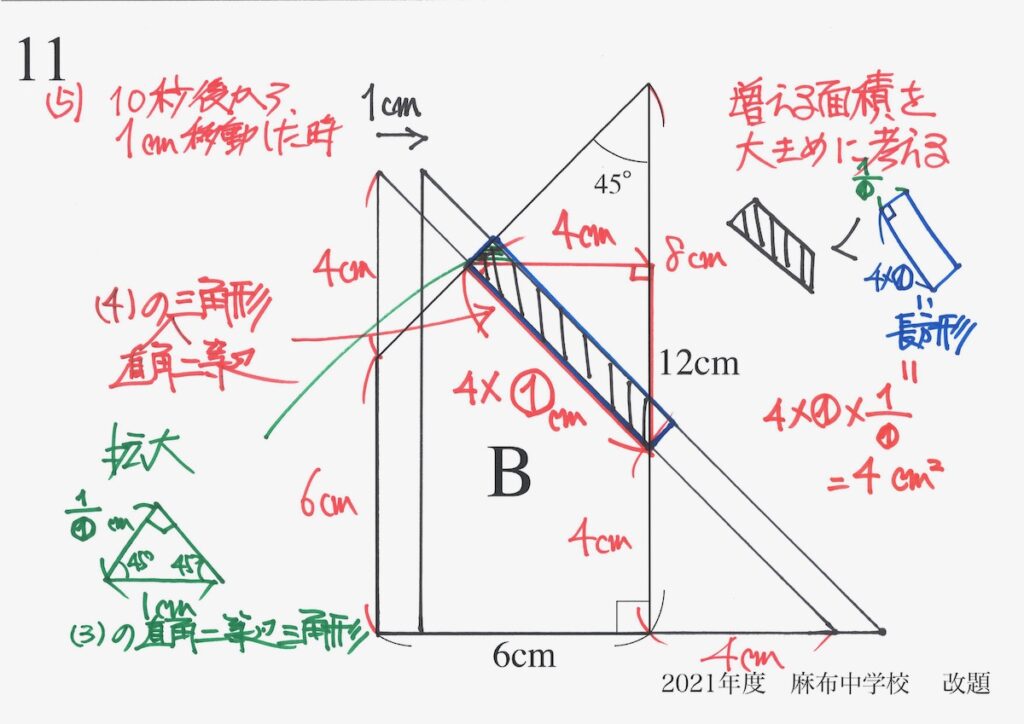

増える面積を少し大きめに考えて、長方形の面積と比較しました。
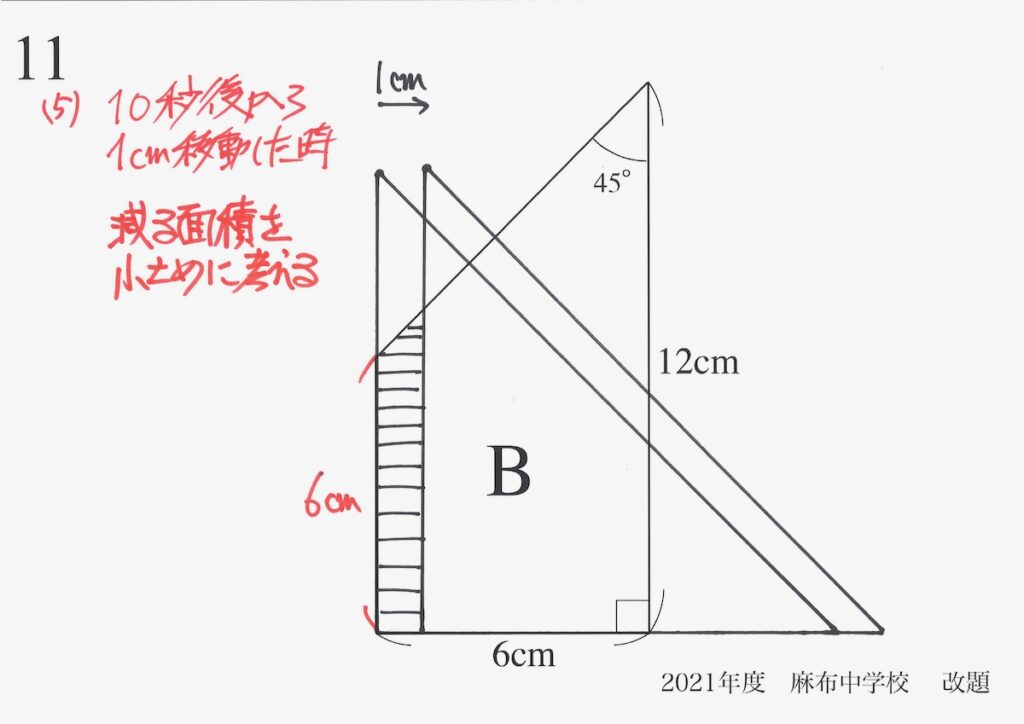

同じように、「減る面積」を少し小さめにしましょう。



さっきと同じように
長方形と比較してみようかな・・・
ここで、「比較して評価するとき」は「大きいと小さいを意識すること」が大事です。
・あるものの大小を比較:大きいと小さいを意識
・「大きい」と予想した対象は「より大きく」そして「小さい」と予想した対象は「より小さく」
「増える面積を大きく考えた」ので、今度は減る面積を小さく考えましょう。
増える面積を大きくした面積=S、減る面積を小さくした面積=Tとします。
「S < T」が言えれば、「増える面積 < S < T <減る面積」となります。
先ほどは、「斜め」だったですが、今回は垂直な長方形と比較しましょう。



「減る面積」だから、
「少し小さくなる」ようにするんだね!
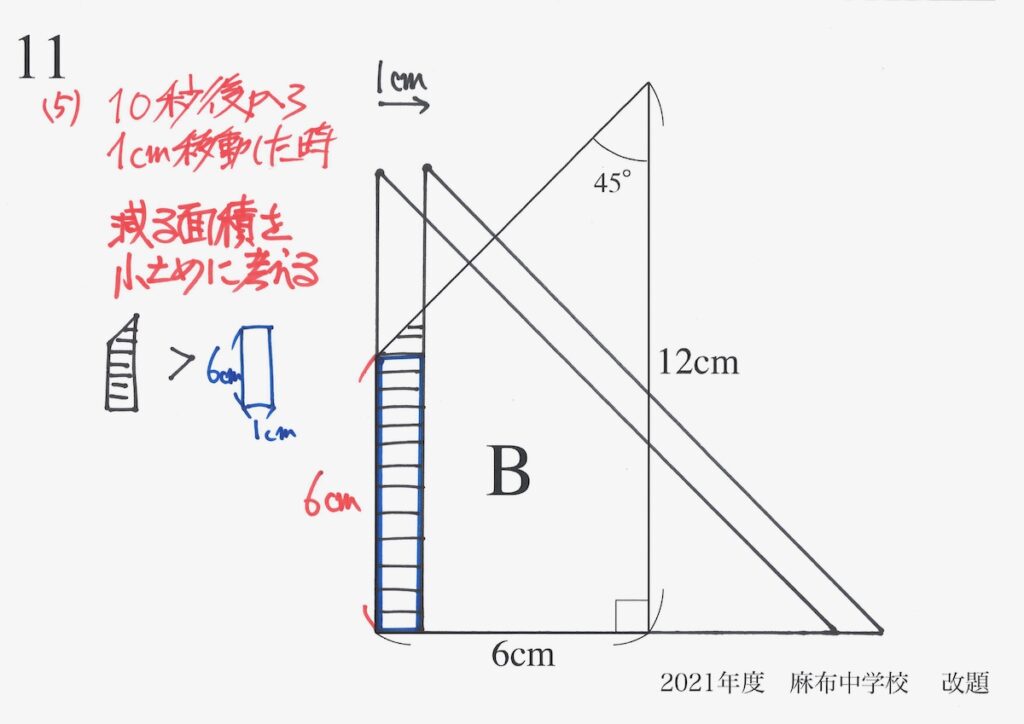

「減る面積 > 上の図の青色の長方形」です。
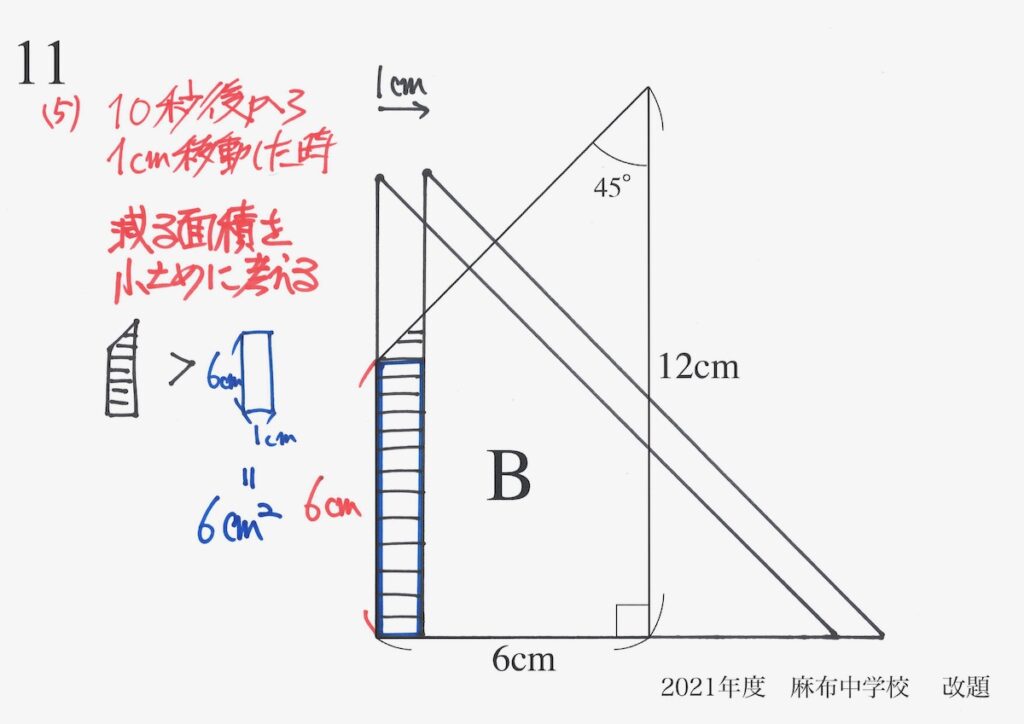

面積は簡単に計算できます。
これで「減る面積が6cm2より大きい」事実が分かりました。
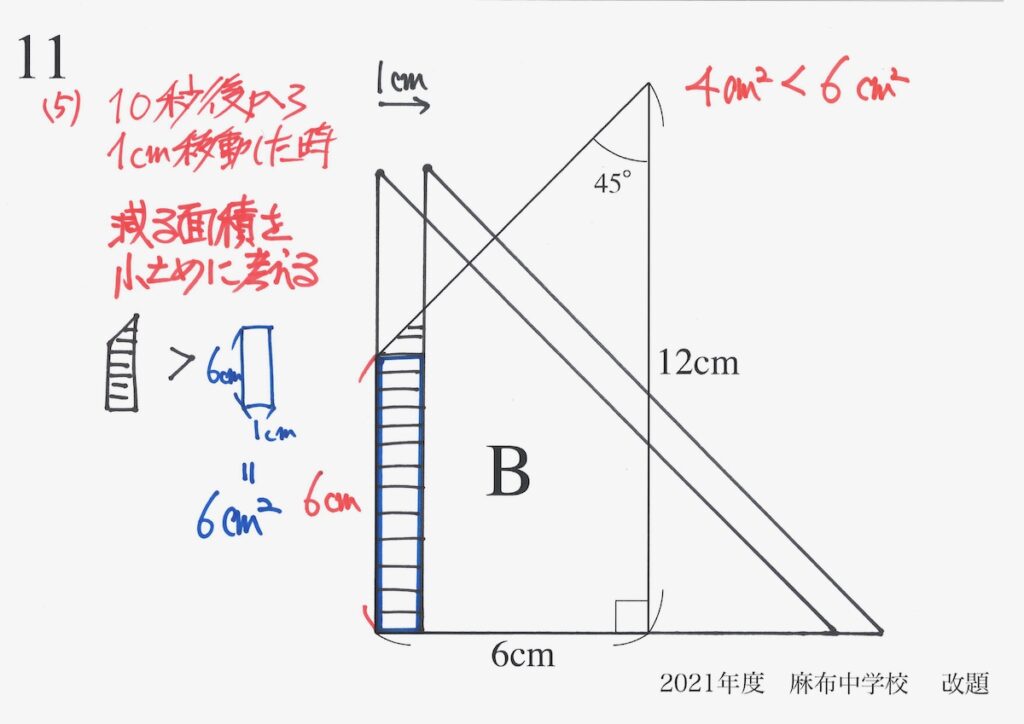




これで、減る面積は
「6cm2より大きい」って分かったね!
具体的に大小を比較
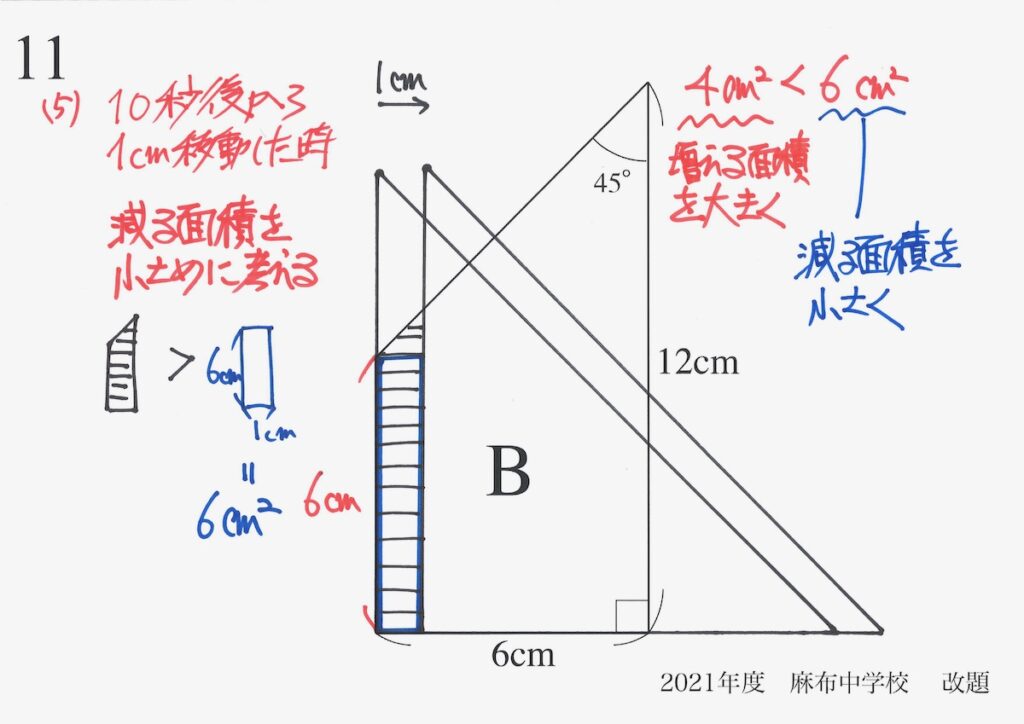

「増える面積 < 4cm2 < 6cm2 <減る面積」が分かりました。



これで、
減る面積と増える面積が比較できたね!
「増える面積を大きくした面積 < 減る面積を小さくした面積」と分かりました。
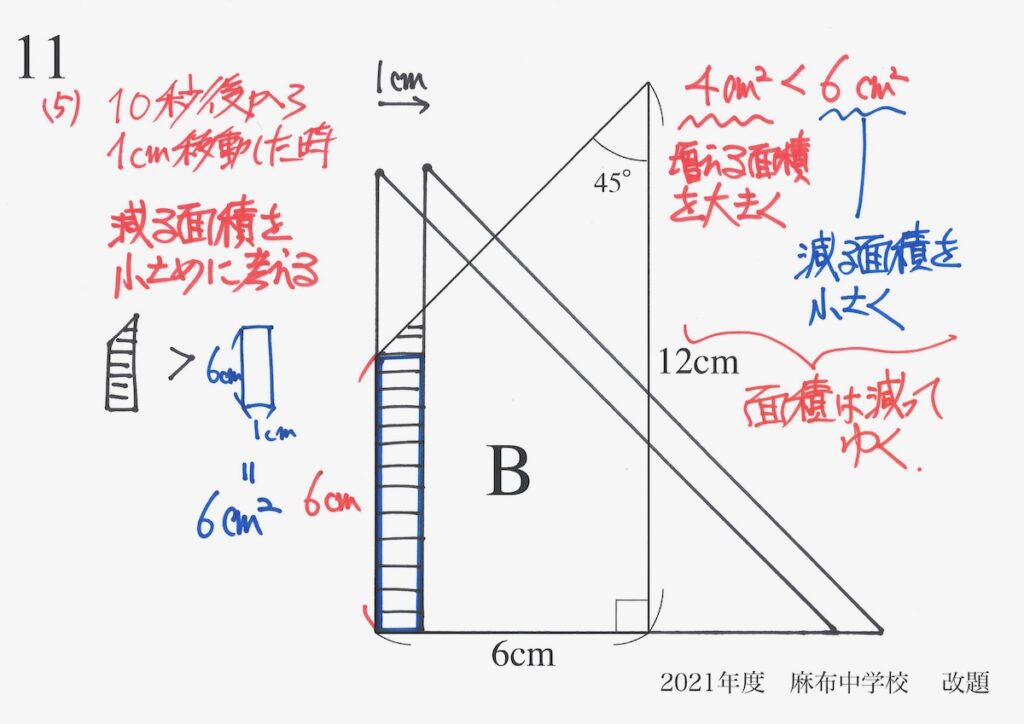

これで、「10秒後から面積は減ってゆく」のが分かりました。



でもさ、この話は
「1秒後」の話だよね・・・



「1.5秒後」とか「2秒後」とか
どうなっているんだろう・・・
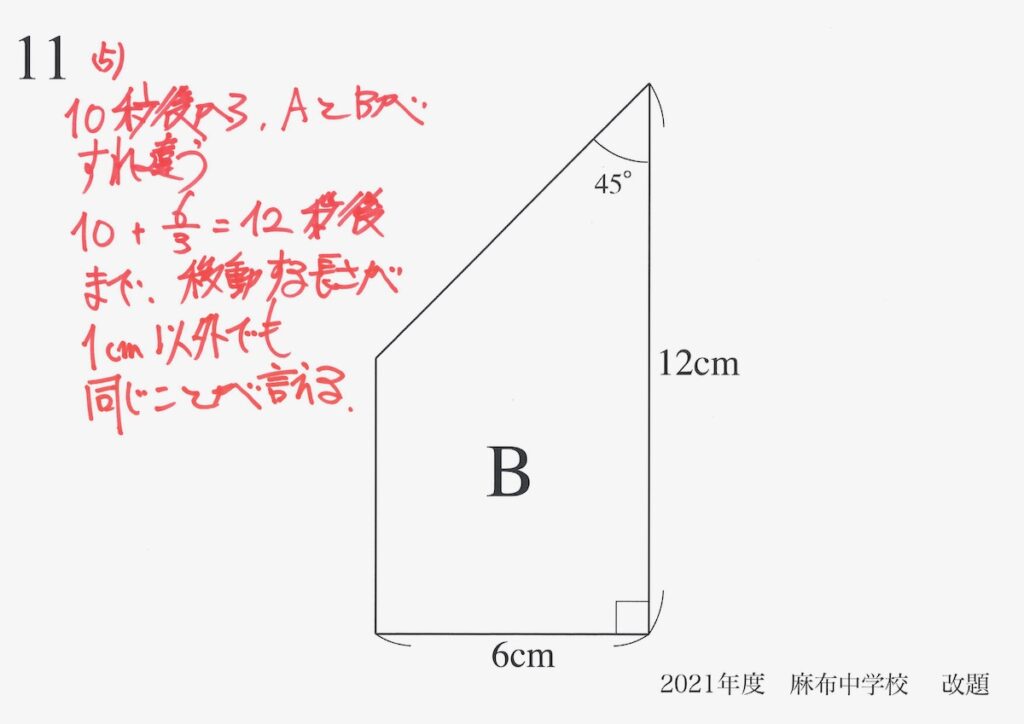

「1cm右に動く状況」を考えましたが、すれ違うまで「同じことが言える」ことです。



確かに「少し動かす」状況は
一緒だから、同じだね。
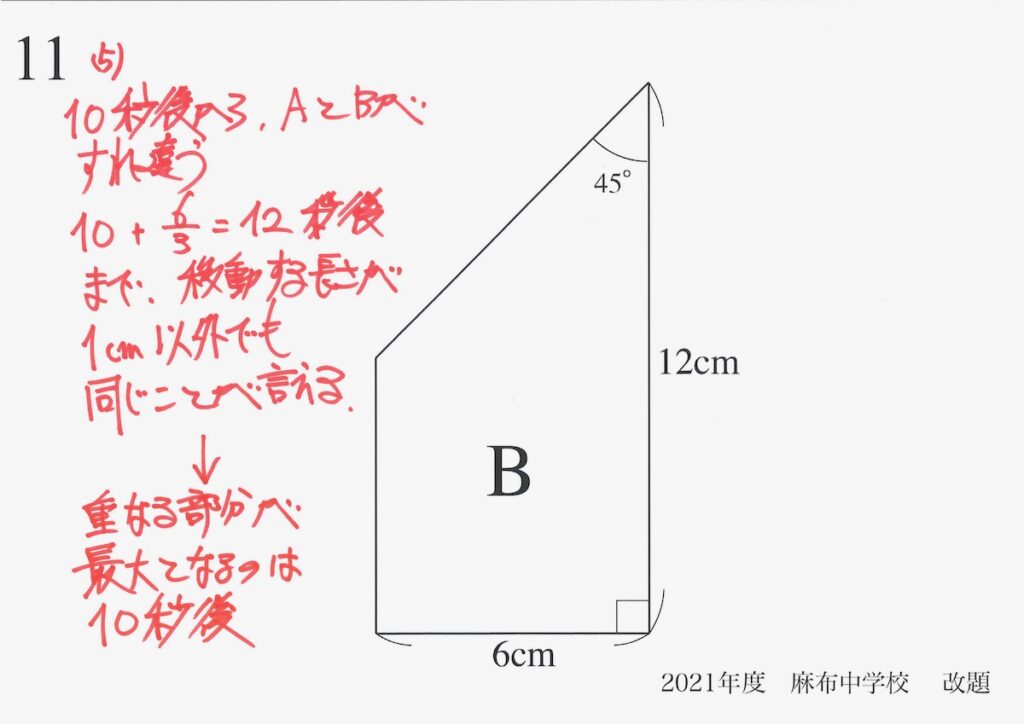

重なる面積が最大となるのは、10秒後と分かりました。
もっと大雑把に考える
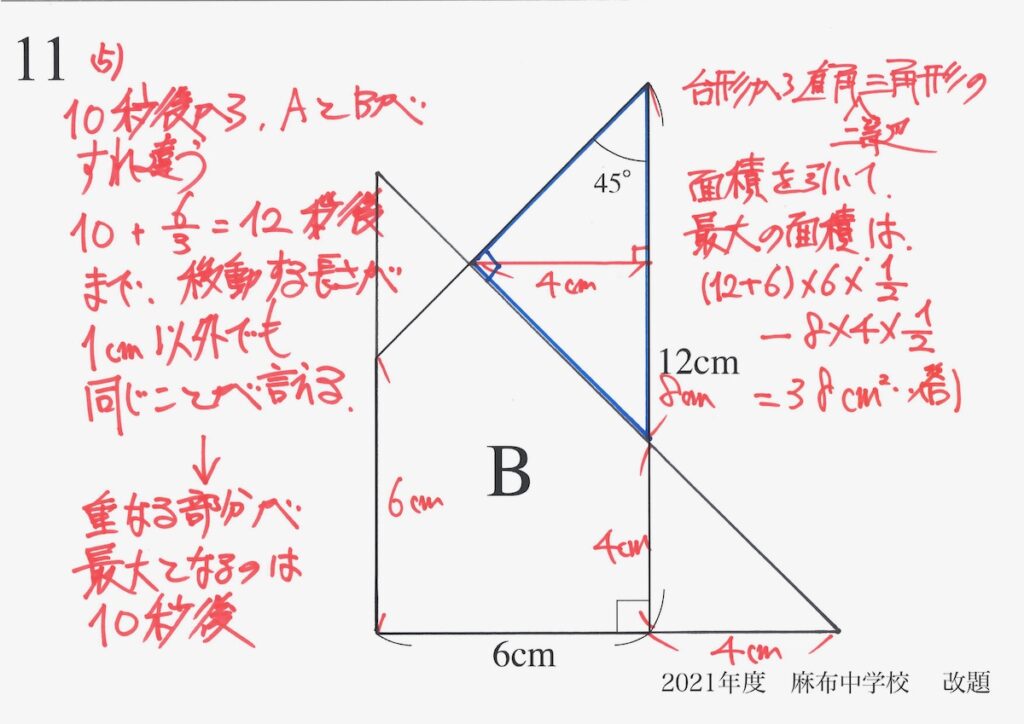

具体的に面積を計算しましょう。
Aは直角二等辺三角形で、Bは「正方形+直角二等辺三角形」です。
そこで、直角二等辺三角形がたくさん出てきます。
面積を比較する際に、「簡単な図形を間に入れる」考え方でした。
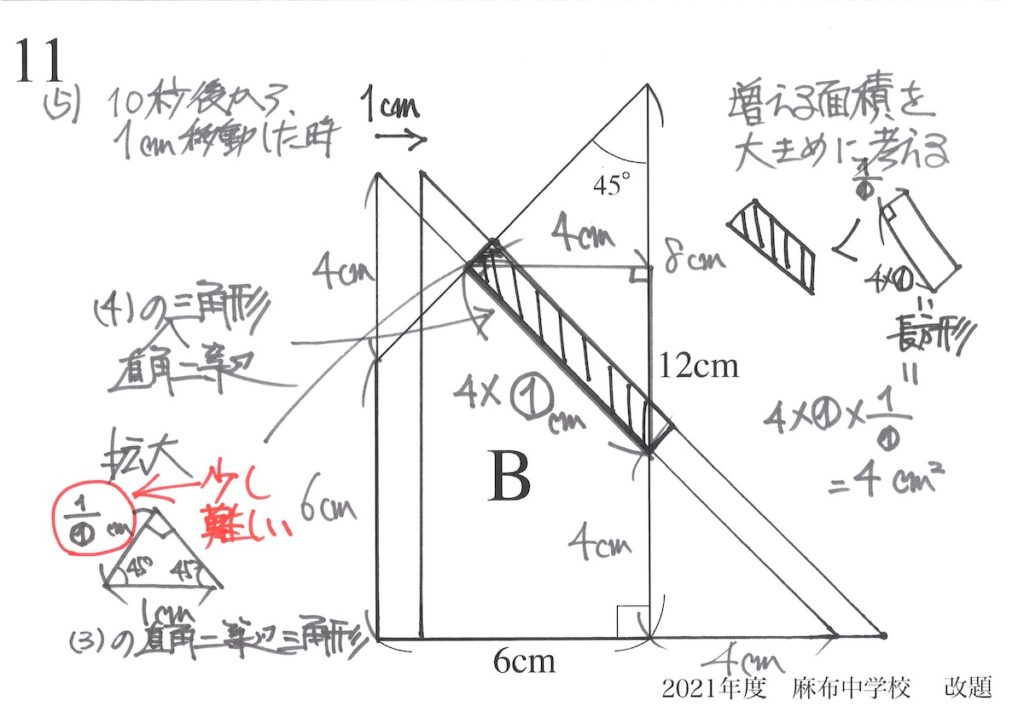

(3)の結果を利用していますが、「よく分からない①で割る」のは、少し数学的な考え方です。



ちょっと
イメージしにくいよ・・・



少し
違和感があるかも・・・
「算数の領域」を逸脱しているようにも感じます。
そこで、上記の「1/①」を考えずに、もっと大雑把に考えてみましょう。



大雑把で
いいの?
少し考えてみましょう。
次回は下記リンクです。



