前回は「動く図形の面積のポイント〜二つの図形が動く時・相対的位置・重なる面積の形を追いかける・少し動かして考える・増える面積と減る面積・問題 11(5)解法〜」の話でした。
問題11(5)（再掲載）
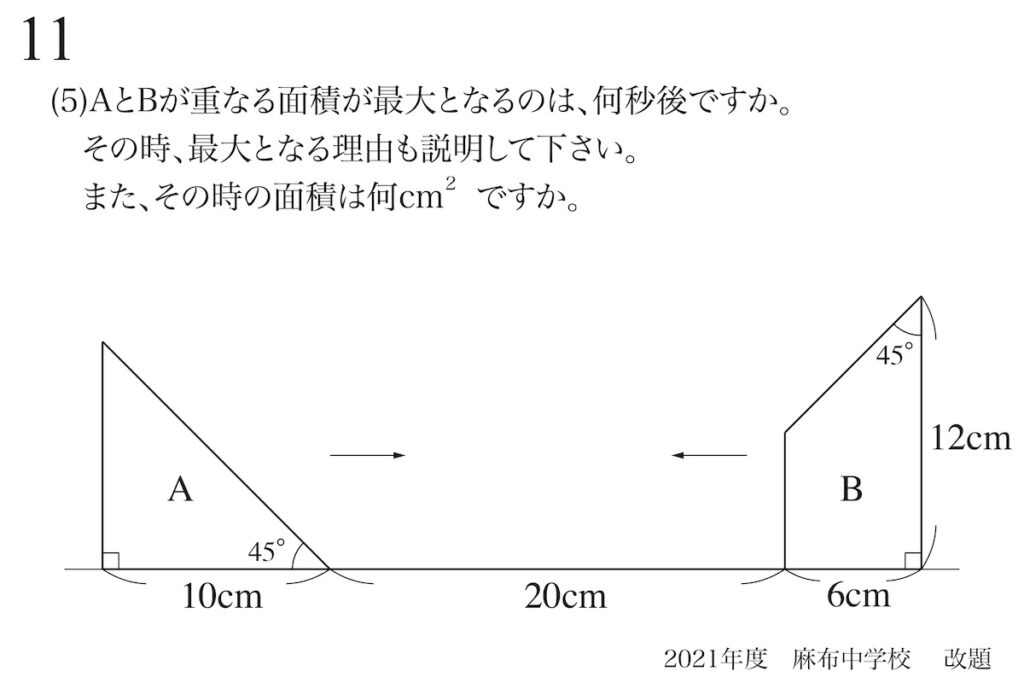
比較する図形を簡単にする：台形と長方形
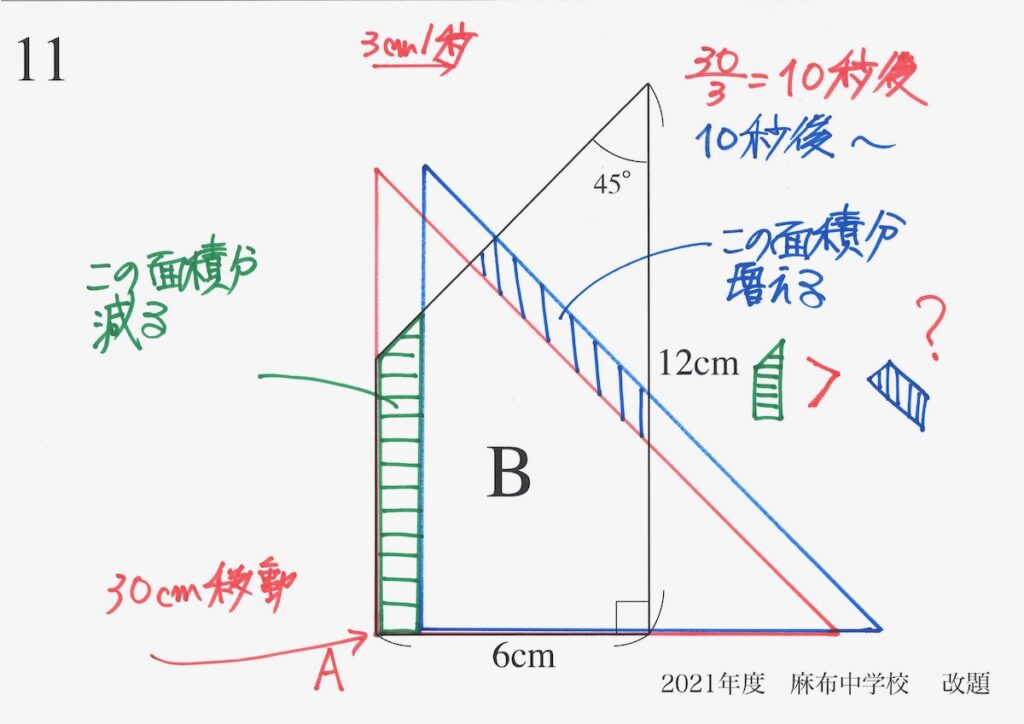
重なる面積が増え続けた後の状況を、「Aの図形を少し右に動かして」考えてみました。
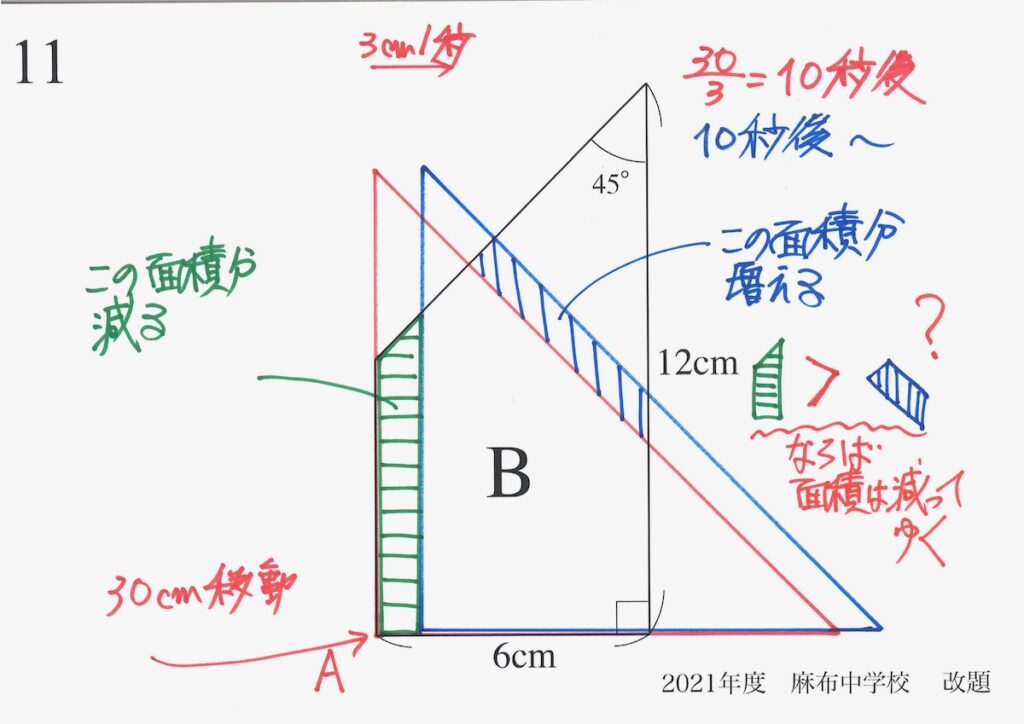
「減る面積 > 増える面積」になりそうです。
そこで、「減る面積 > 増える面積」を説明することを考えましょう。
両方とも形は台形です。
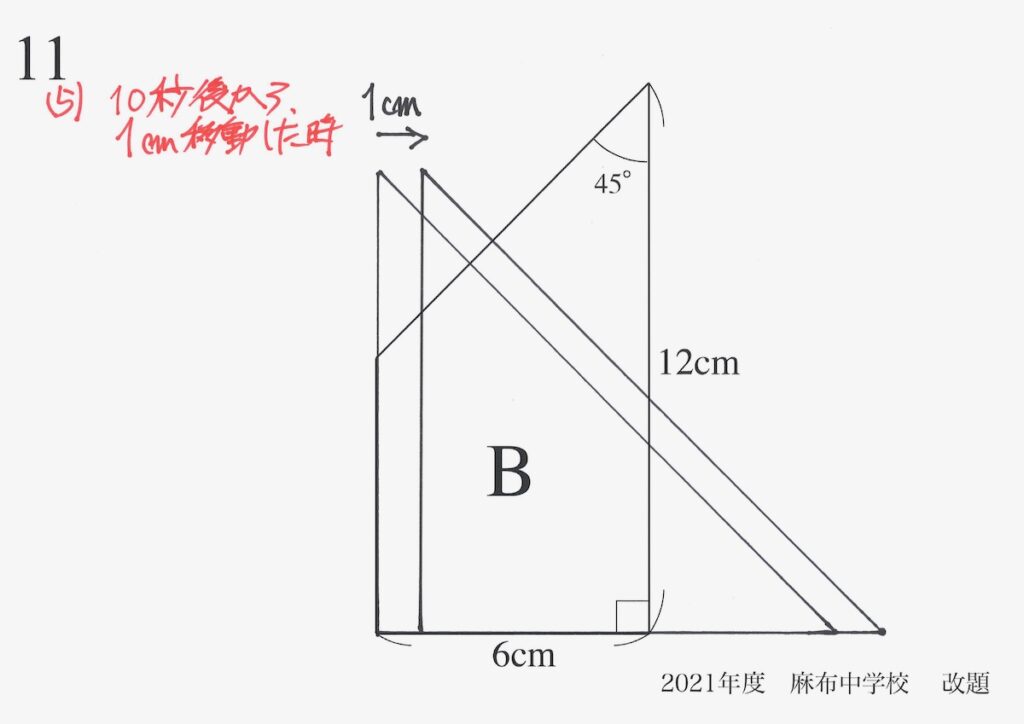
ここで、具体的に「10秒後から1cmAが移動した状況」を考えましょう。
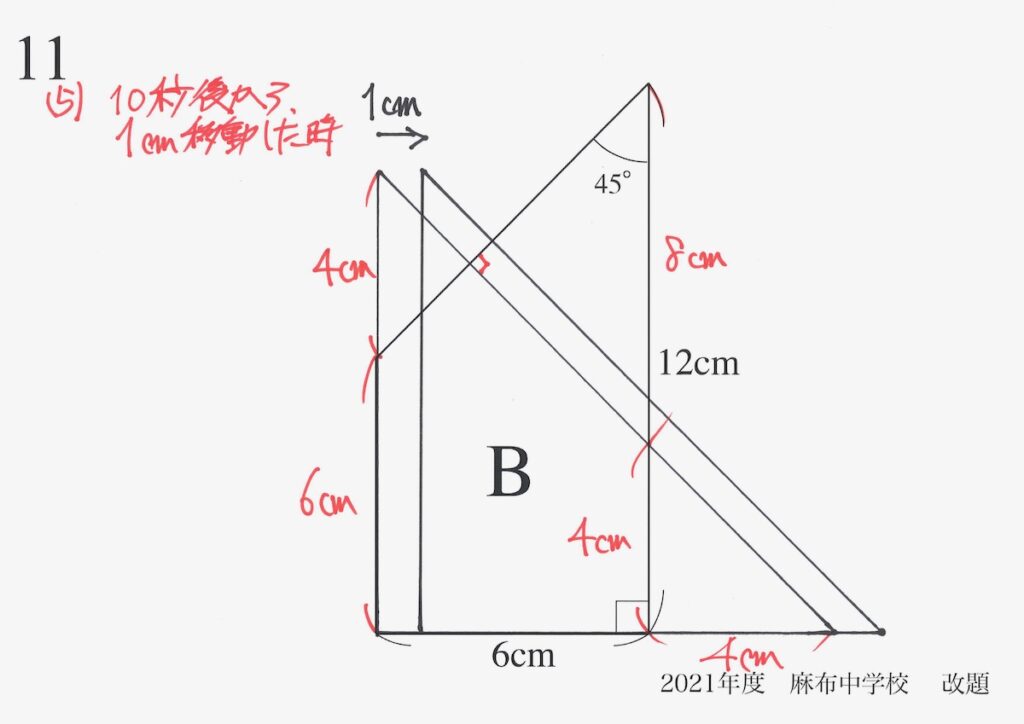
分かる長さを書いてみましょう。
A、Bの図形は、直角二等辺三角形があるので、重なると直角二等辺三角形が次々に生まれます。
男子小学生なんとなく、
イメージは湧くけど・・・
女子小学生ちょっと
難しいかも・・・
前回は「少し後」を考えましたが、今回は具体的に「1秒後」を考えます。
前回描いた図とは、「増える面積」と「減る面積」は見るからに大きさが違います。
女子小学生やっぱり、減る面積の
方が大きい気がする！
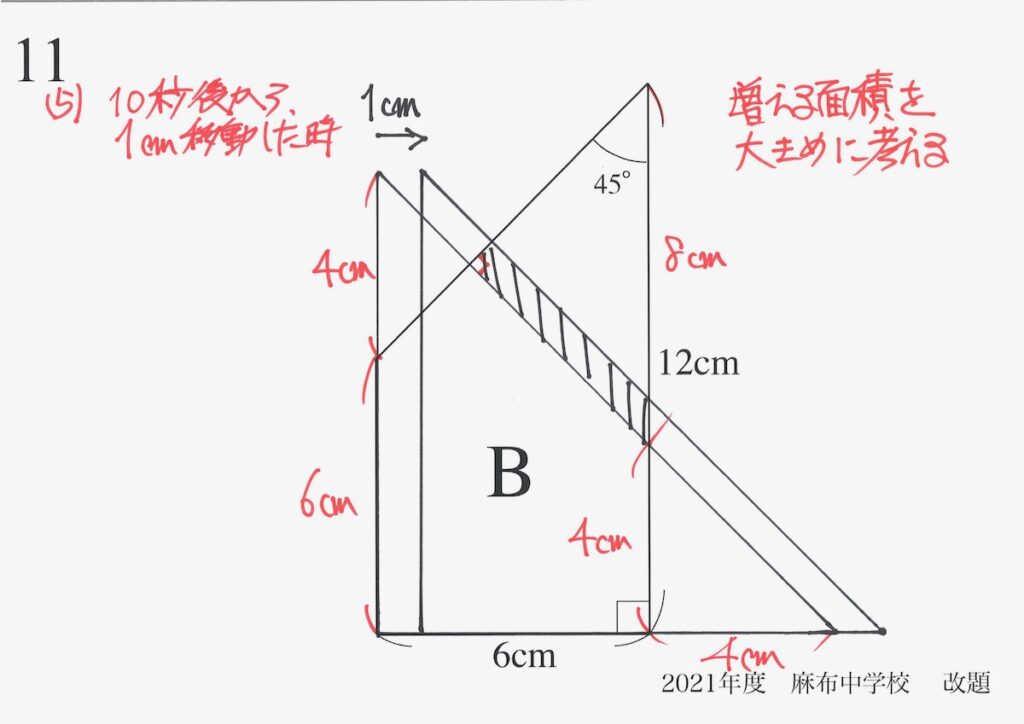
そこで、「増える面積」を大きめに考えてみましょう。
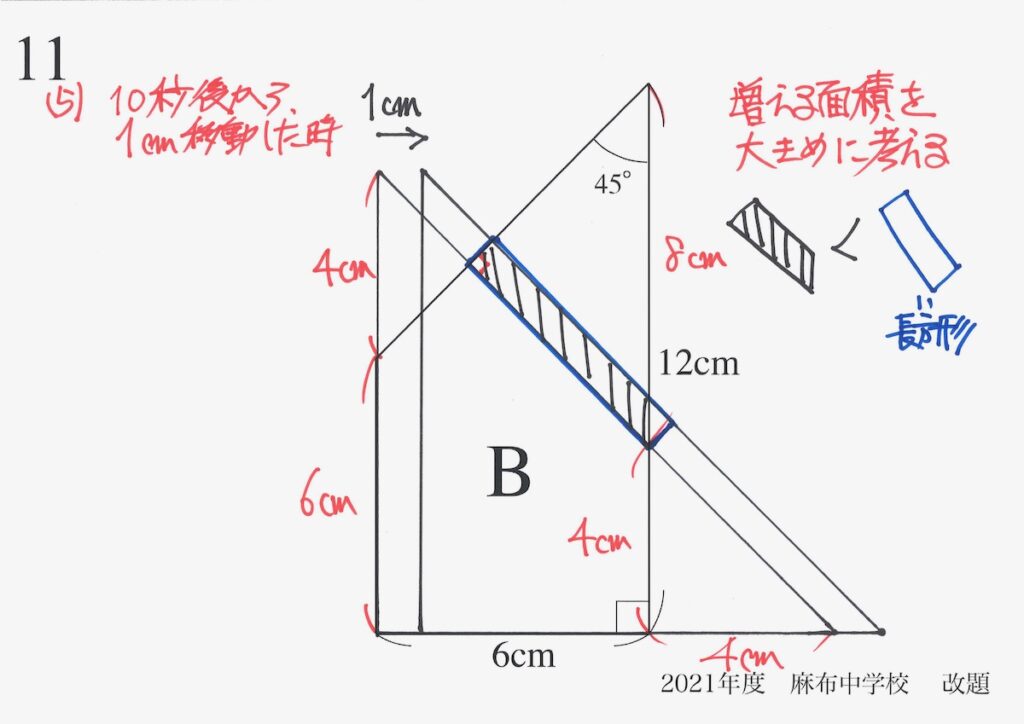
増える面積は、上の図の青色の長方形より、面積が小さいです。
男子小学生増える面積を
勝手に増やしていいの？
台形よりも長方形の方が「考えやすい」ので、少し増やして考えてみましょう。
最終的に「増える面積 < 減る面積」が分かるようにしたいです。
そこで、「増える面積を少し大きくして」比較します。
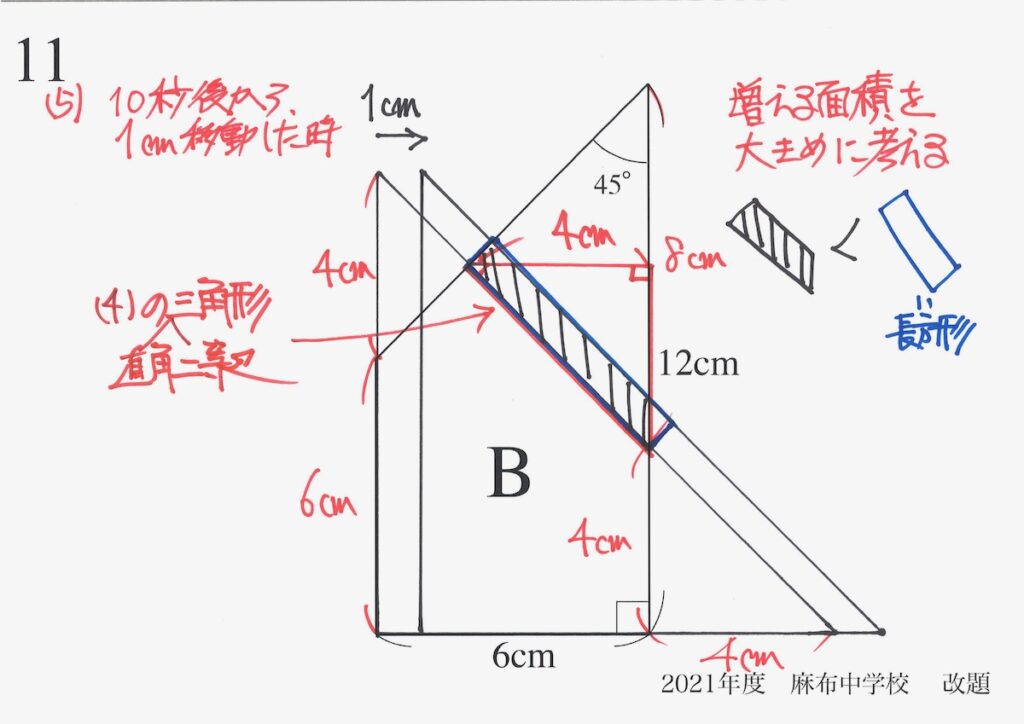
分かる長さを描いてゆくと、「(4)で考えた直角二等辺三角形」が出てきます。
女子小学生ここで、「前の問題がヒント」という
考え方が役立ちそうだね！
1.最後の問題のみだと難しいため、ヒントを作って解きやすくする
2.問題を分け、出来る部分を明確にして、採点の際に点数の差が出やすくする
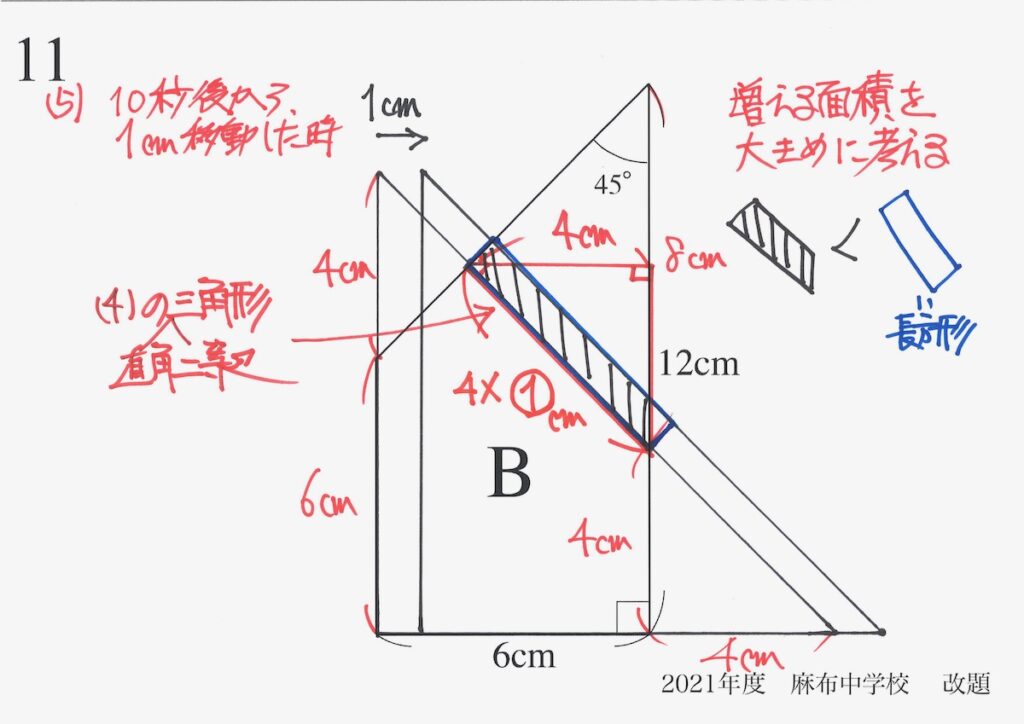
これで、青色の長方形の「長い辺の長さ」が分かりました。
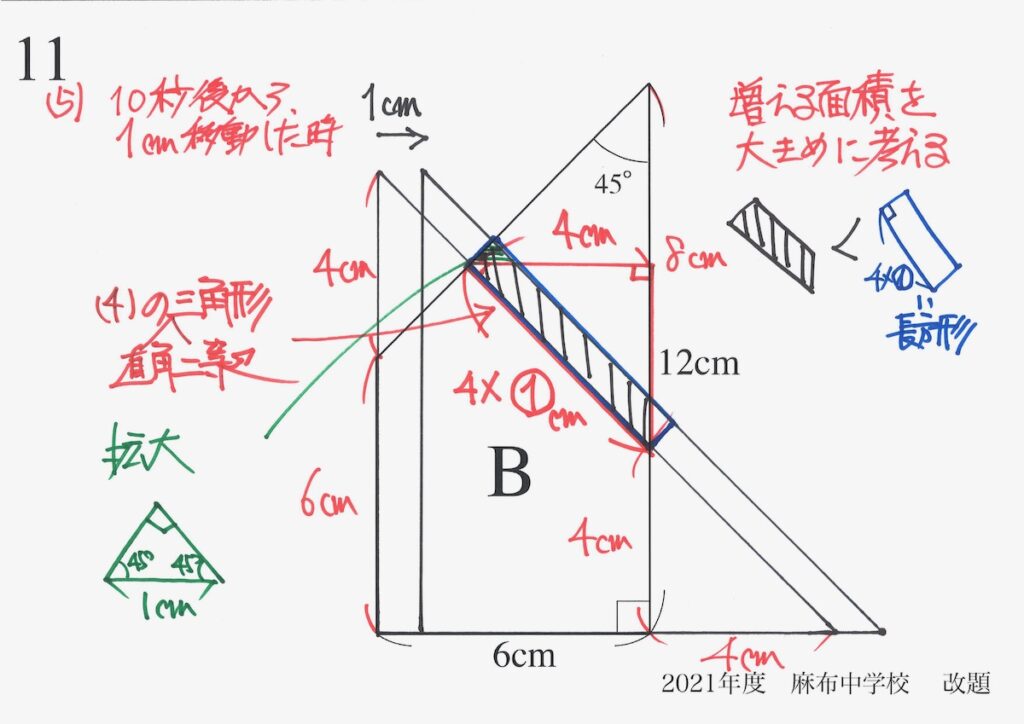
次は、青色の長方形の「短い辺の長さ」を考えましょう。
青色の長方形の左上の部分を拡大してみましょう。
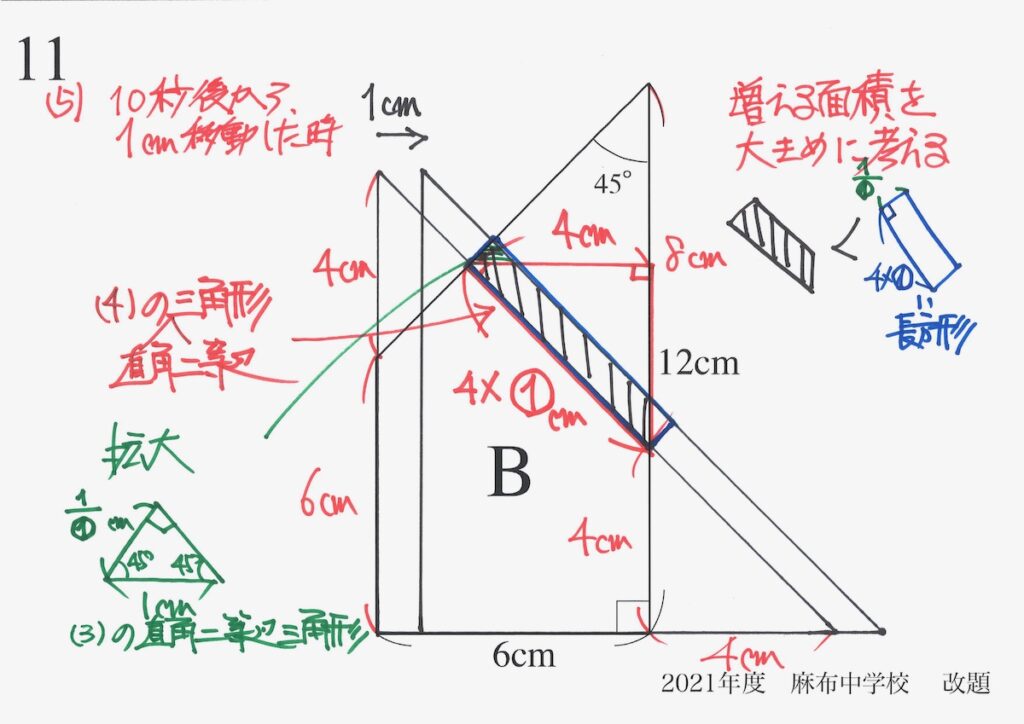
すると、直角二等辺三角形が現れます。
この直角二等辺三角形は(3)と似ています。
ここでは、「斜辺の長さが1cm」で、(3)では「等しい辺の長さ1cmのとき、斜辺の長さ①cm」でした。
そこで、この緑色の直角二等辺三角形の「等しい辺の長さ=1/①cm」です。
これで、青色の長方形の辺の長さが分かりました。
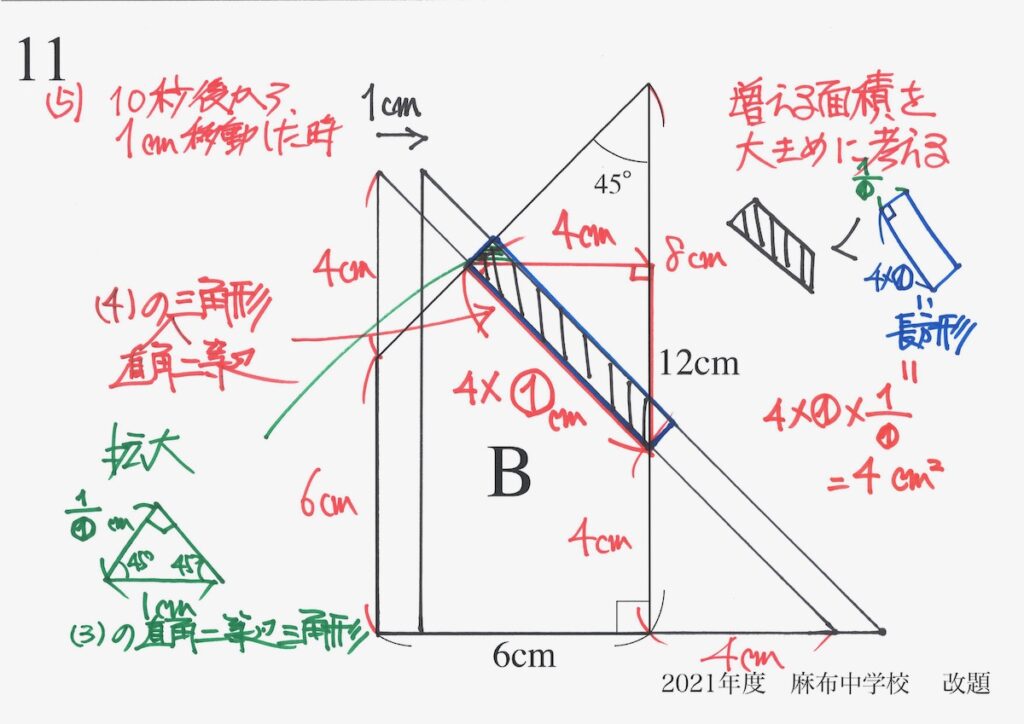
面積を計算すると、4cm2となります。
これで、「Aが1cm右に移動した時、増える面積は4cm2より小さい」と分かりました。
減る面積を簡単な図形と比較
「増える面積を大きく考えた」ので、今度は減る面積を小さく考えましょう。
増える面積を大きくした面積=S、減る面積を小さくした面積=Tとします。
「S < T」が言えれば、「増える面積 < S < T <減る面積」となります。
女子小学生比較する対象を変えるって
ことだね！
男子小学生勝手に自分で大きくしたり、小さくしても
比較する対象の大将が分かればいいんだね！
「増える面積 < 減る面積」から、10秒後が面積の最大となることが言えます。
減る面積は、簡単な面積と比較するように考えましょう。
次回は下記リンクです。
