前回は「向かい合う点の移動が分かるコツ〜電車のイメージ・動く点の片方を止める・「速さを足す」理由と矢印・問題11(1)解法AB〜」の話でした。
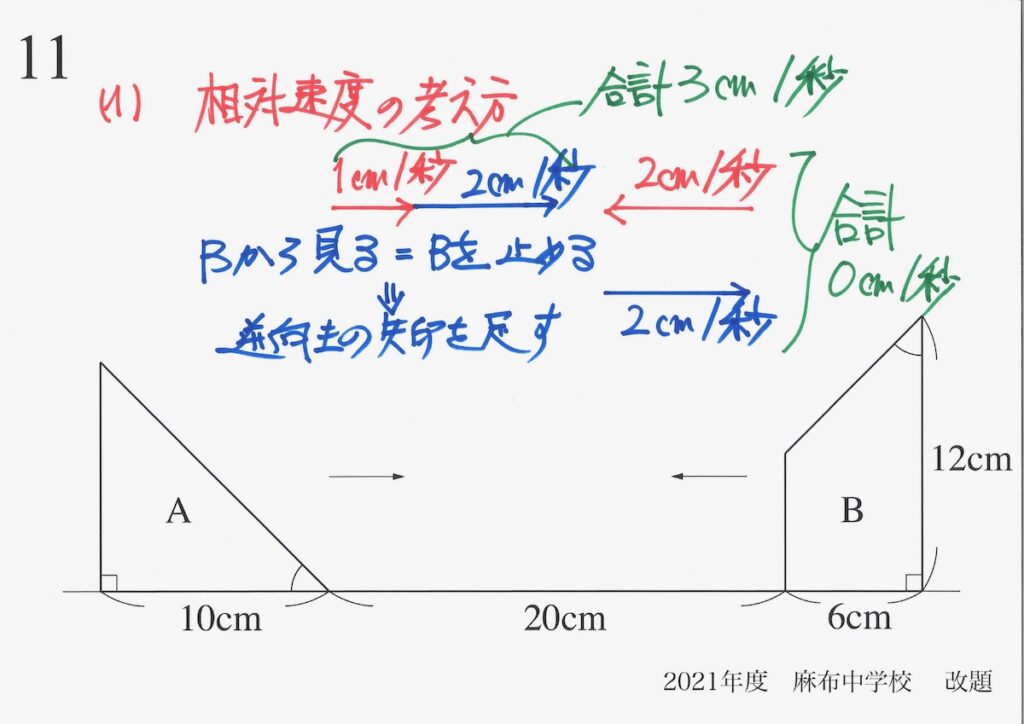
問題11（再掲載）
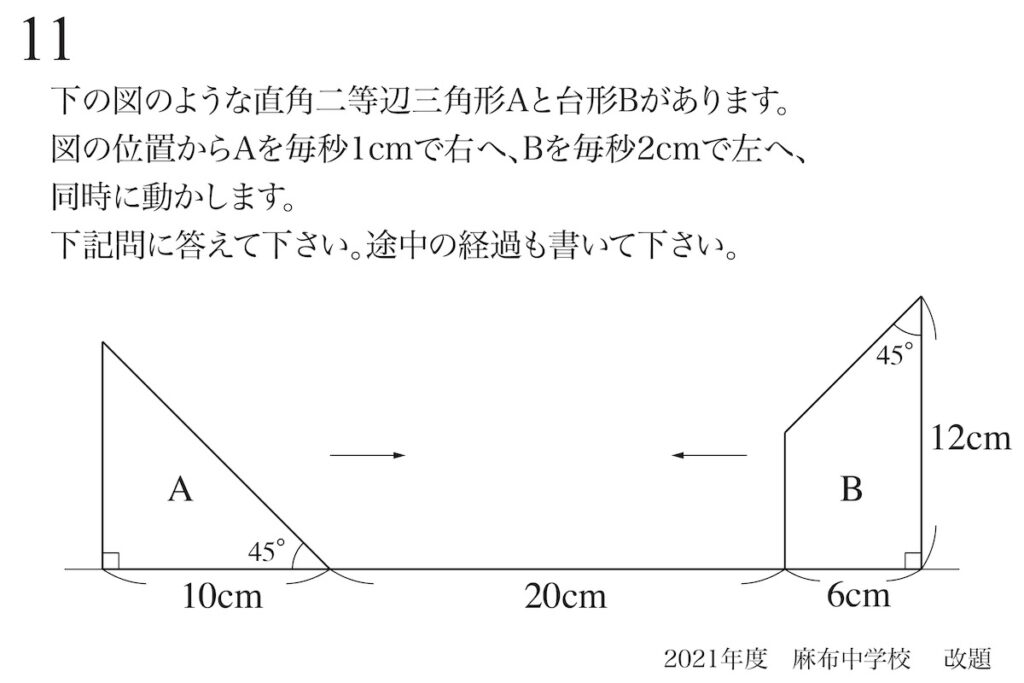
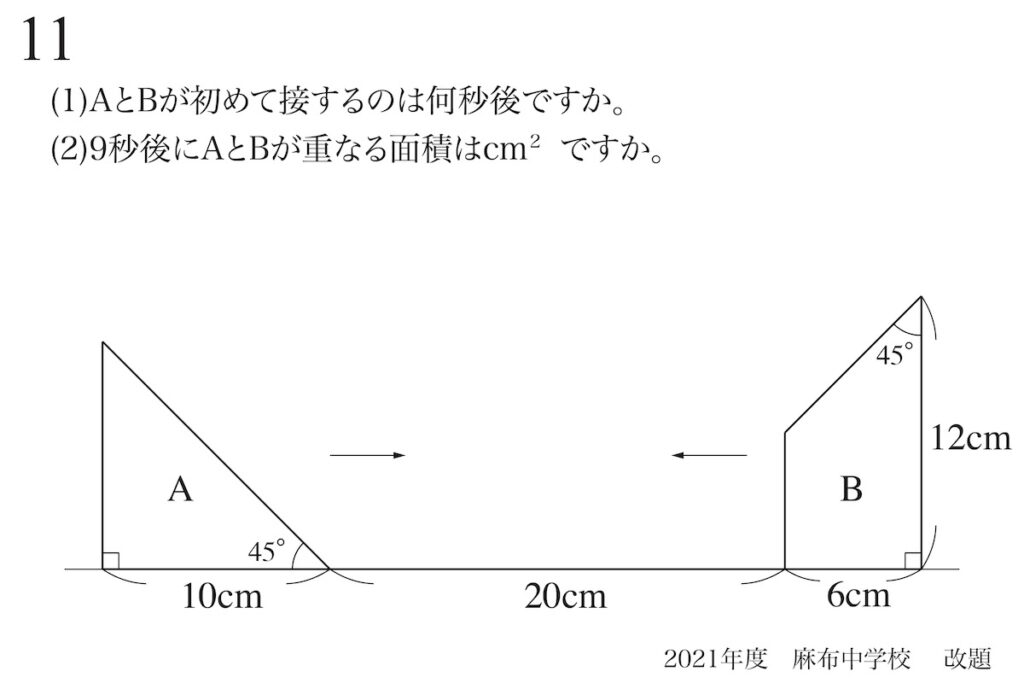
二つの移動する図形が分かるポイント・コツ
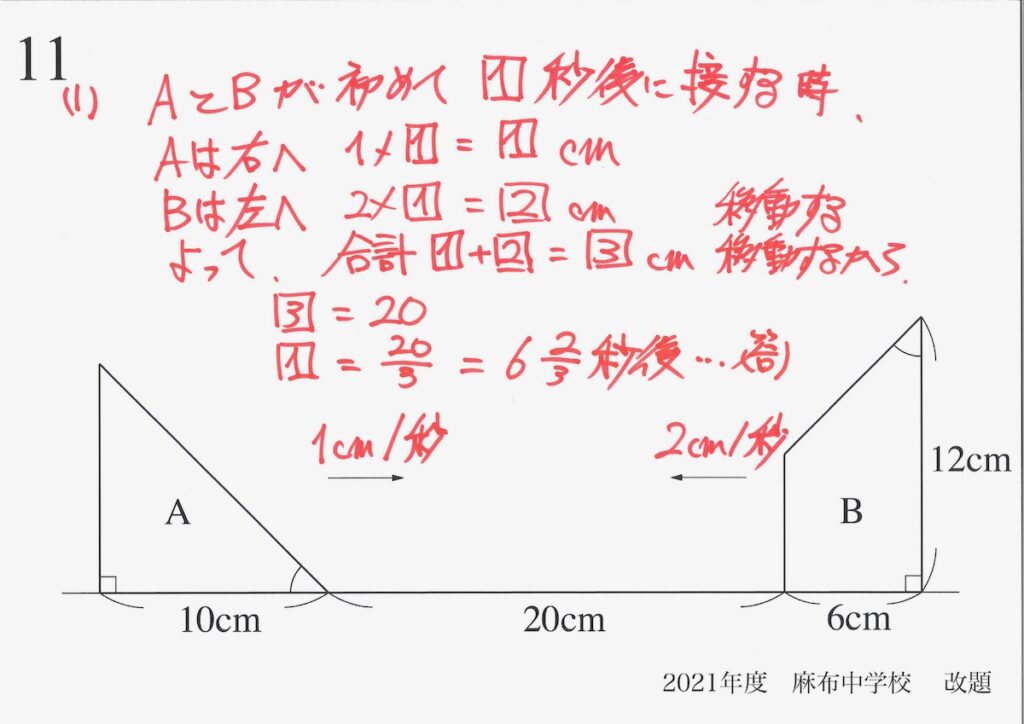
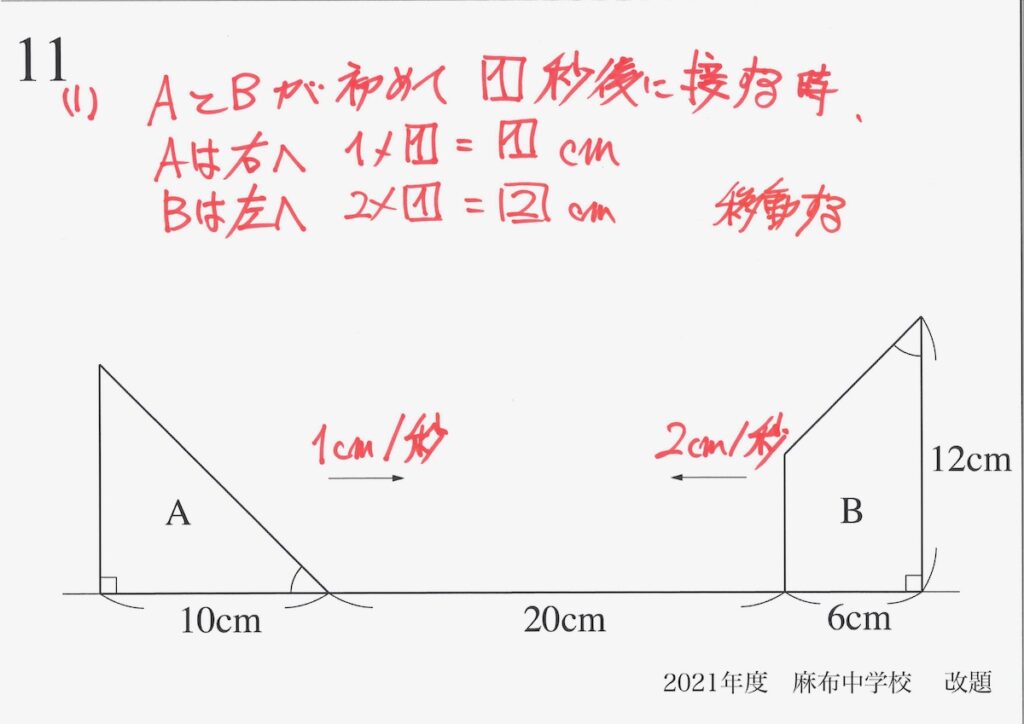
(1)では、未知数を設置する方法と相対的速さを考える方法を考えました。
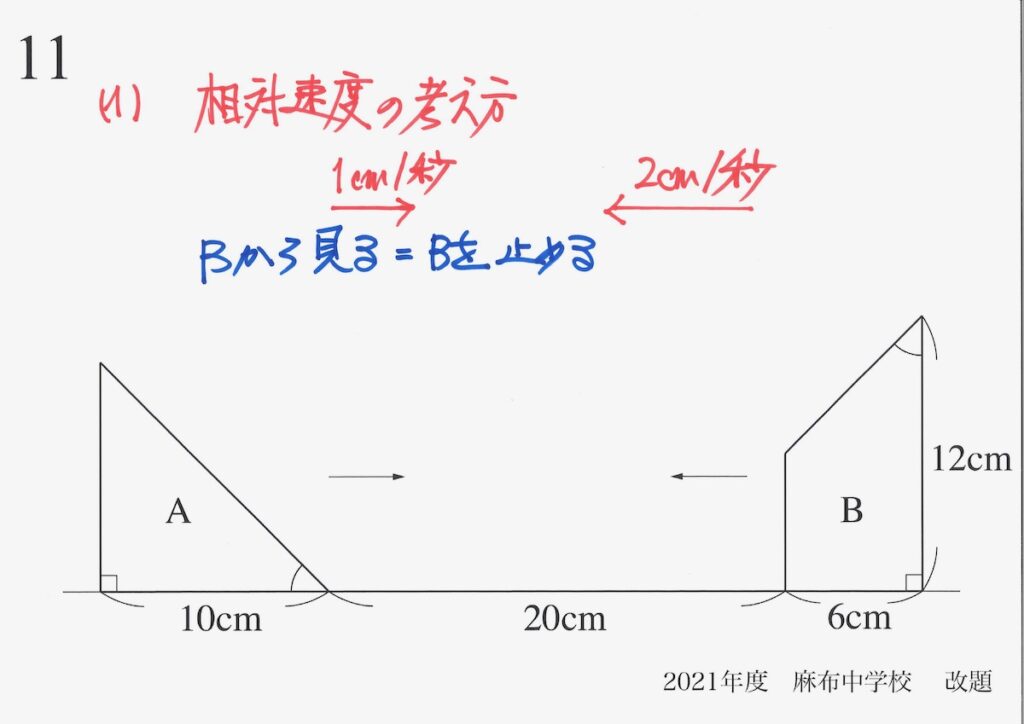
このように「動く図形・点の問題は片方止める」では、イメージして理解することが大事です。
「向かい合う図形の速さは合計（和）になる」ことを矢印でしっかり理解しましょう。
(2)のように、図形や点などが二つ動いて「〜秒後の状況」を考える問題があります。
男子小学生とりあえず、「一つを止める」って
習ったよ。
こういう時は「一つを止めて考える」のが、いわゆる「鉄則」です。
この考え方は非常に有効ですが、「鉄則」というよりも「考え方をしっかり理解」しておきましょう。
中学の算数で「動く二点の問題」のご紹介をしました。
これらの問題で「二点、二つが動く時」の考え方が紹介されています。
ただ「一つ止めれば良い」と考えていると、応用力が伸びない傾向があります。
そして、少し変化球の問題になると、
男子小学生どう考えたら
いいのかな？
応用問題や難問に対して、対応しにくくなることがあるでしょう。
二つ・二点動く時は、「一つを止める」のは「相対的な位置を重視する」姿勢です。
相対的位置：「変化しない量」は大事なポイント
「一つを止める」あるいは「片方から見る」方が、考えやすいことがあります。
それら動く図形・点などが「それぞれの位置」よりも「相対的位置」の方が重要な時に大事です。
女子小学生「なぜ、相対的位置が大事か」を
考えてみれば良いのね。
今回の問題では、一度、それぞれの図形を動かしてみても良いでしょう。
9秒後の状況を、具体的に考えてみて絵を描いてみましょう。
男子小学生9秒後の具体的な
図形を描いてみるね！
二つ動く問題は、難しいです。
それは、「片方を考えている間に、もう片方が動いてしまう」からです。
考える対象が二つになると、非常に難しく感じてしまいます。
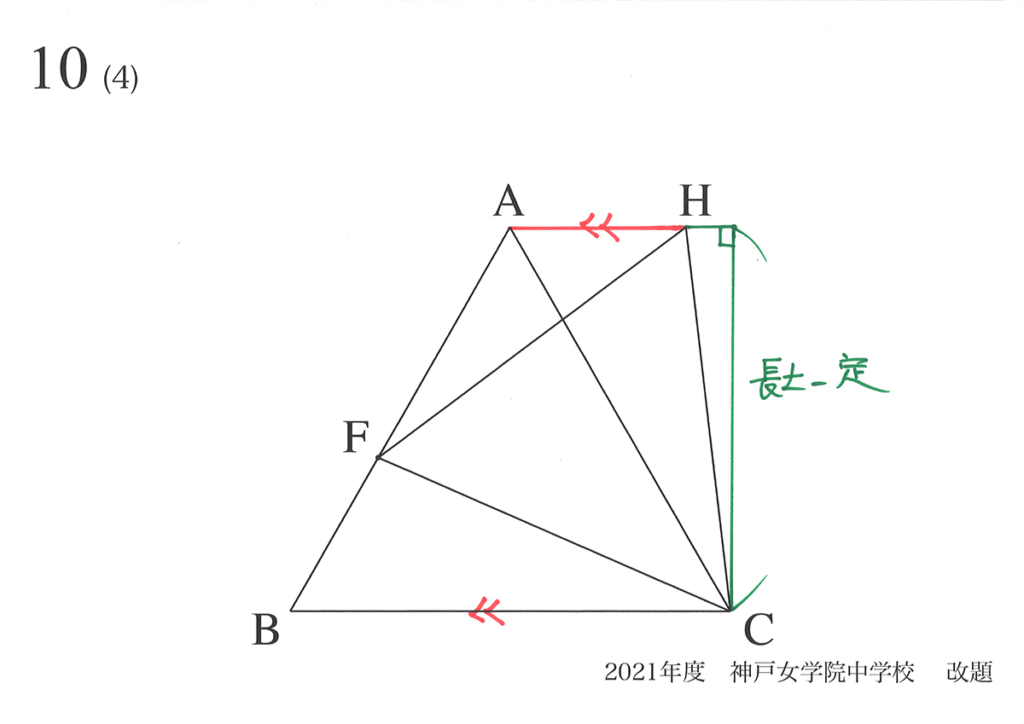
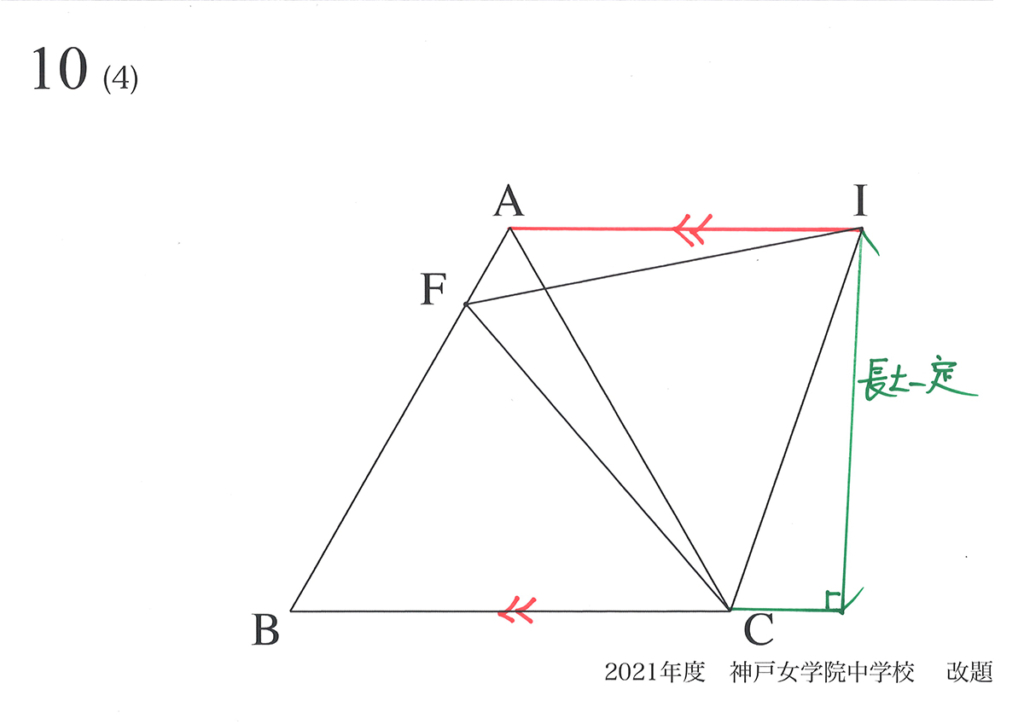
動く点の問題で「変わらないモノ（長さ）に注目」する話をご紹介しました。
「算数実践 54」では、「ある長さが変わらない（不変）」であることに注目しました。（上記リンク）
「二つの図形・点などが動く」時は、「変わらないモノは何かな？」と考えてみましょう。
今回の問題では、「変わらないモノ」は何でしょうか？
男子小学生変わらない
モノ・・・
女子小学生二つの図形は、
それぞれ動くから・・・
男子小学生それぞれ動く速さは、
変わらないね。
女子小学生そうね。
「Aから見た速さ=Bから見た速さ」で、変わらない！
Aが右に1cm/秒で、Bが左に2cm/秒で進んで、
相対的な速さは「お互いが3cm/秒で近づく」ことで、「変わらないモノ」です。
「変わらない長さ」や「変わらない速さ」など「変化しない量」は大事なポイントです。
このことを、しっかり理解して考えてみましょう。
解法は次回（下記リンク）ご紹介します。
