前回は「動点Pの攻略法〜動く点の行動範囲と対称性・面積が最小となる時・直角三角形の基本性質〜」の話でした。
問題10(4)再掲載
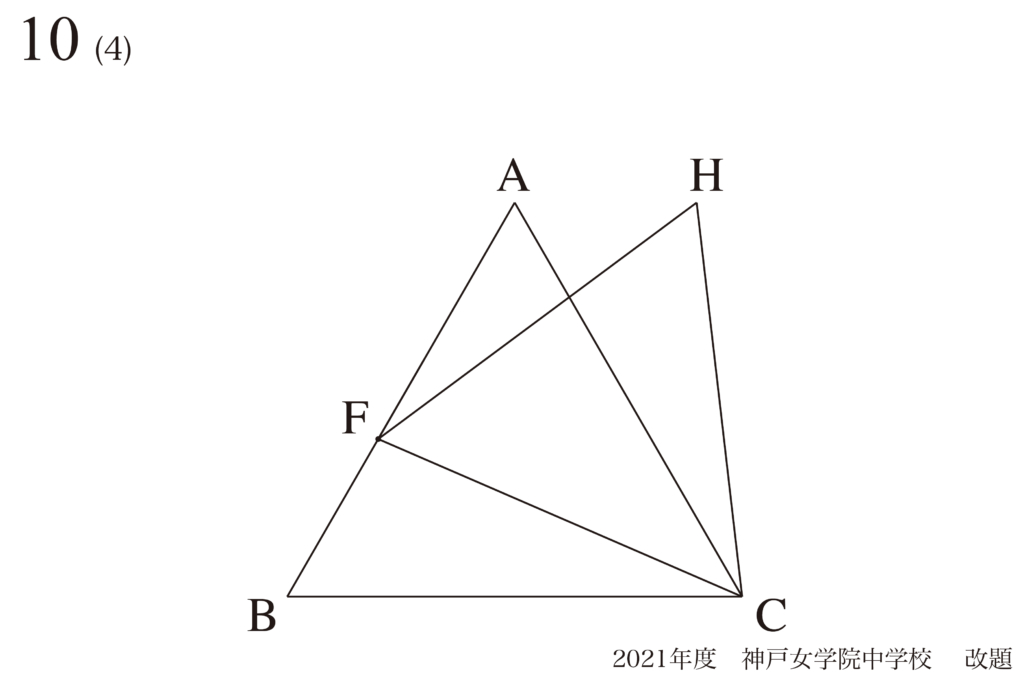
動点Pの問題が「できない」から「できる」へ：変化しない量・長さ・モノに注目
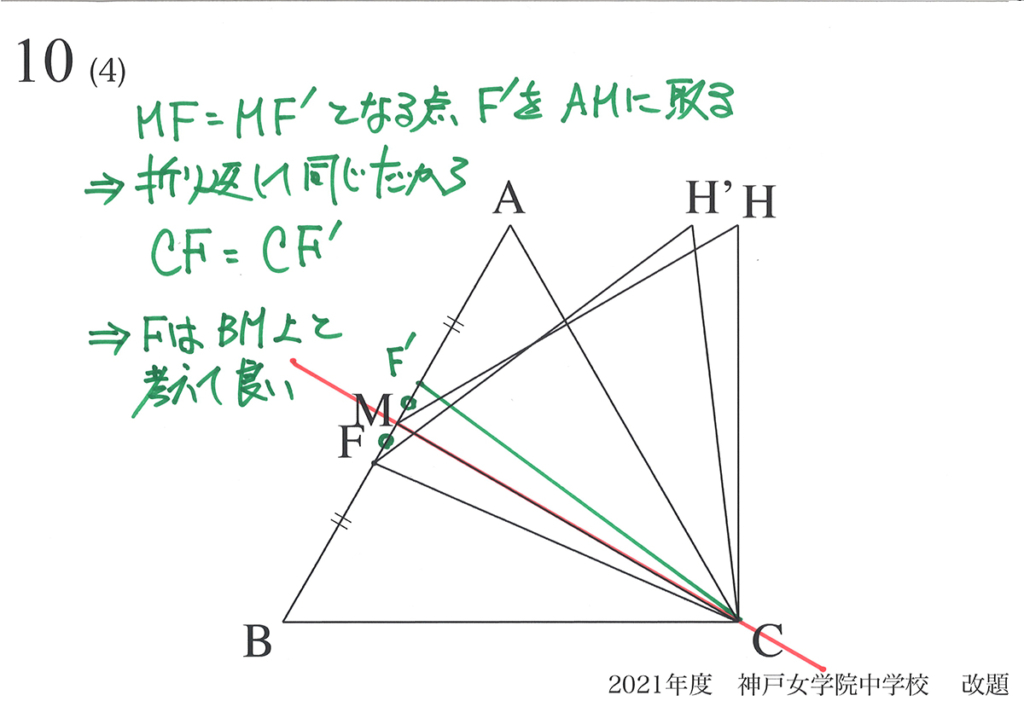
「面積が最小となる」時を考えるために、まず動く点Pの動く範囲を絞りました。
動く点Pが「辺ABを動く」から「辺BMを動く」状況を考えればよく、「半分になった」のです。
女子小学生考えなければならないのが、
半分になるのは、とても助かる！
男子小学生これは、とても
考えやすくなるね！
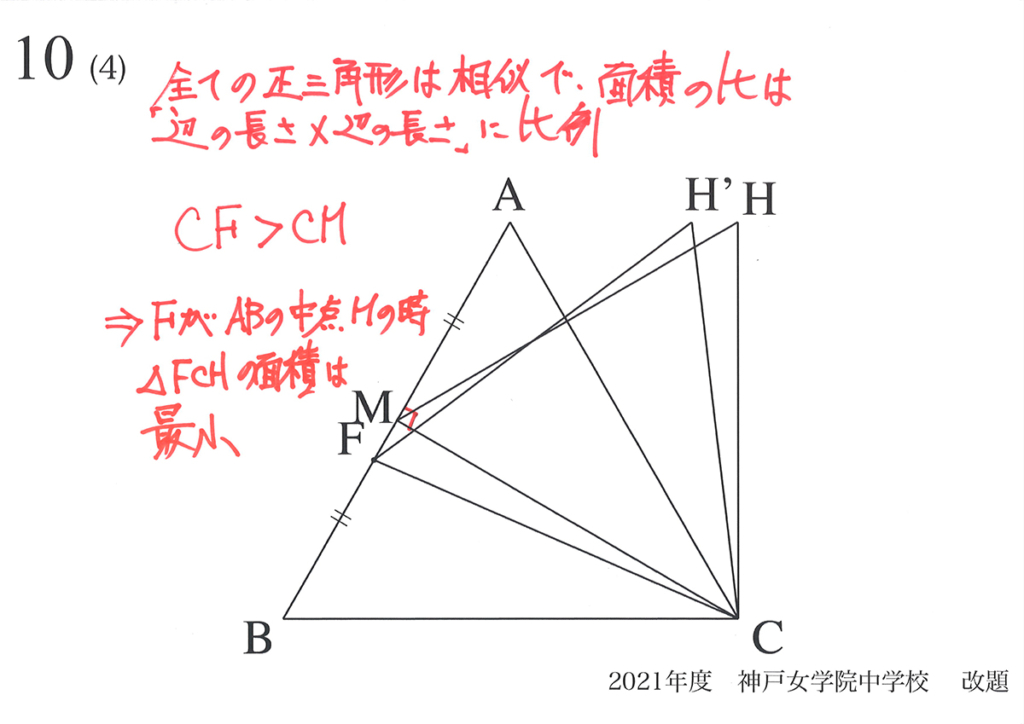
ここで、「相似比=辺の比 x 辺の比」から、正三角形の「一つの辺の長さの比較」を考えました。
すると、「面積が最小」が「長さが最小」となる時を考えればよく、とても簡単になりました。
男子小学生「面積が最小」って、
難しいよ・・・
男子小学生でも、「長さが最小」なら
分かりやすいかもね。
簡単になったのは、理由があります。
「長さ」は一次元で分かりやすいのに対して、「面積」は二次元で「二つの長さが関係する」からです。
・長さは「cm」「m」など一次元
・面積は「cm2「「m2」 など、「単位に小さな2がつく」二次元
面積は、例えば「100平方センチメートル」と表現しますが、この「平方」が二次元です。
・比較する対象の次元を小さくできないか、考える
・面積は「長さx長さ」で二次元、長さは一次元なので、一次元の方が簡単
面積の計算の仕方は、様々な図形の形によります。
基本的には三角形に分割できるので、「底辺 x 高さ /2」です。
解法Aの良いところは、相似形の面積比は「辺の長さの相似比が分かれば良い」点に注目したことです。
これで、面積を考えるために、動くモノが二つ（辺と高さ）だったのが、一つになりました。
そのため「非常に考えやすくなった」のです。
女子小学生確かに、二つ同時に変わるから
難しかったけど・・・
女子小学生動くのが一つだったら、
簡単になるね！
男子小学生動く点の問題は、
簡単に考えるコツが分かれば、できそう！
2つのモノが動く時：変化しないモノは何か
(4)は、この考え方で解けましたが、今回は別の視点から考えてみましょう。
「動く一点を止める」のが「定石」です。
「定石」ですが、「そもそも動いている点を止めて考える」のは不思議です。
男子小学生動いているから、困るのに
勝手に止めていいの？
女子小学生「動く一点を止める」が分からないのは、
算数のセンスがないのかな・・・
「動く一点を止める」のが「不思議に感じる」方が正しい感覚でしょう。
「止める」のが違和感があるようでしたら、「片方が超高速で動いているイメージ」も良いでしょう。
あるいは「相対的位置」を考えると良いでしょう。
二つのモノが動くと、手に負えなくなってしまうのです。
そこで、
男子小学生変わらないものは、
ないかな？
このように「対象を絞ってゆく」考え方は、非常に大事です。
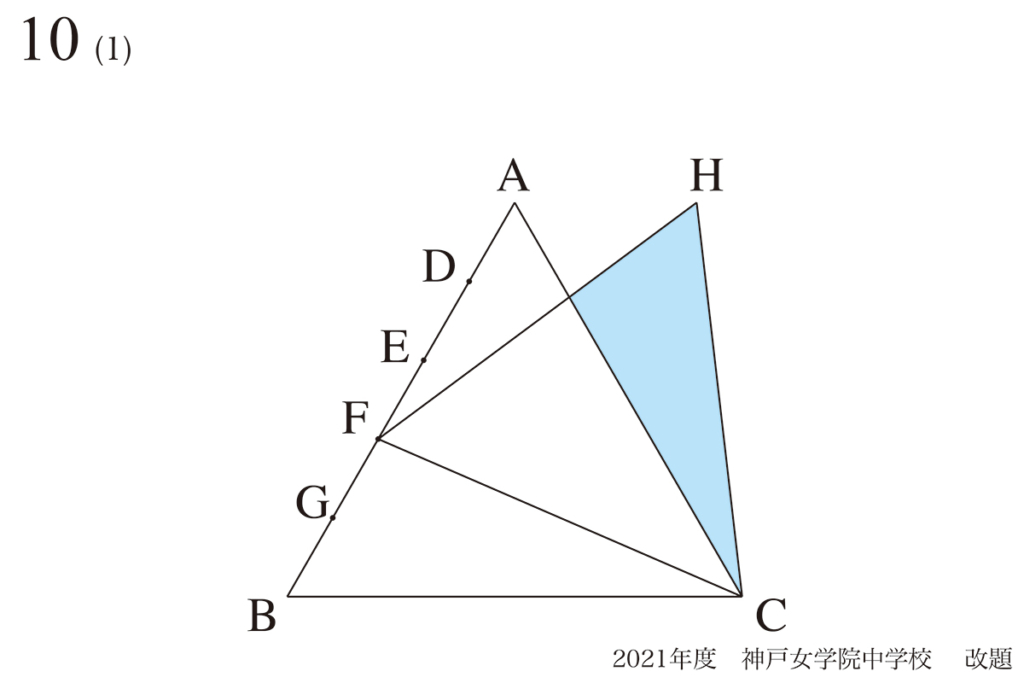
△FCHの面積を考えるに当たって、「変化しないモノ」を考えてみましょう。
ヒントは、最初の方で分かった大事な「平行」です。
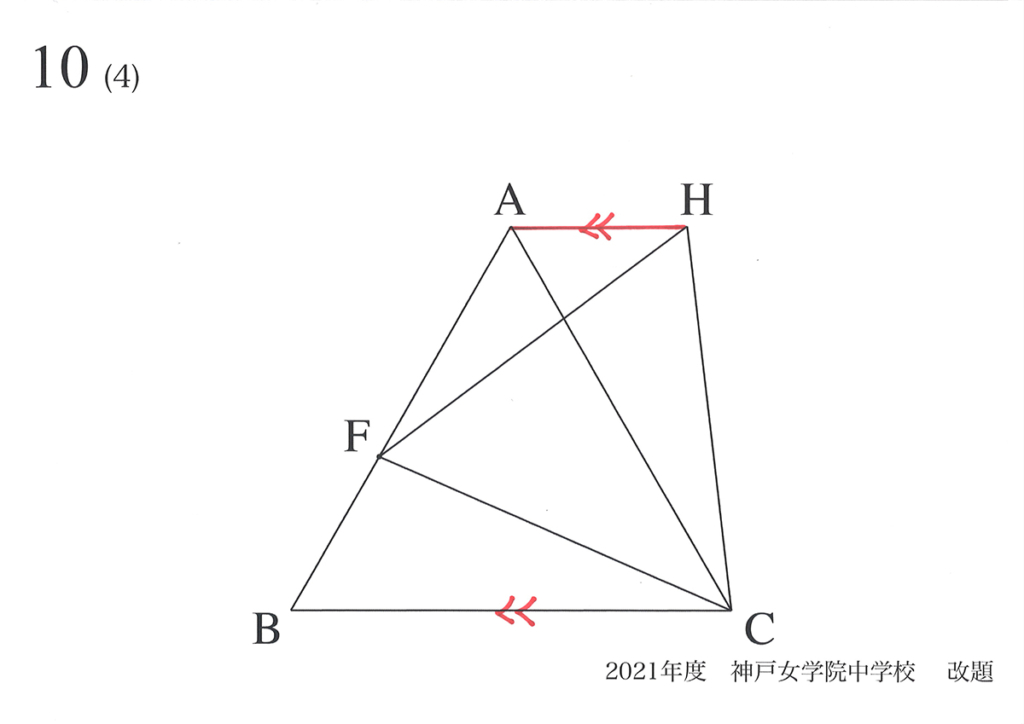
少し試行錯誤して、考えてみましょう。
次回は下記リンクです。
