前回は「動く点と図形の面積のグラフを描くコツ・ポイント〜まずは最大・最小・最も大きな特徴を考える・図形の対称性とグラフの対称性・問題10(5)解法〜」の話でした。
問題10(5)（再掲載）
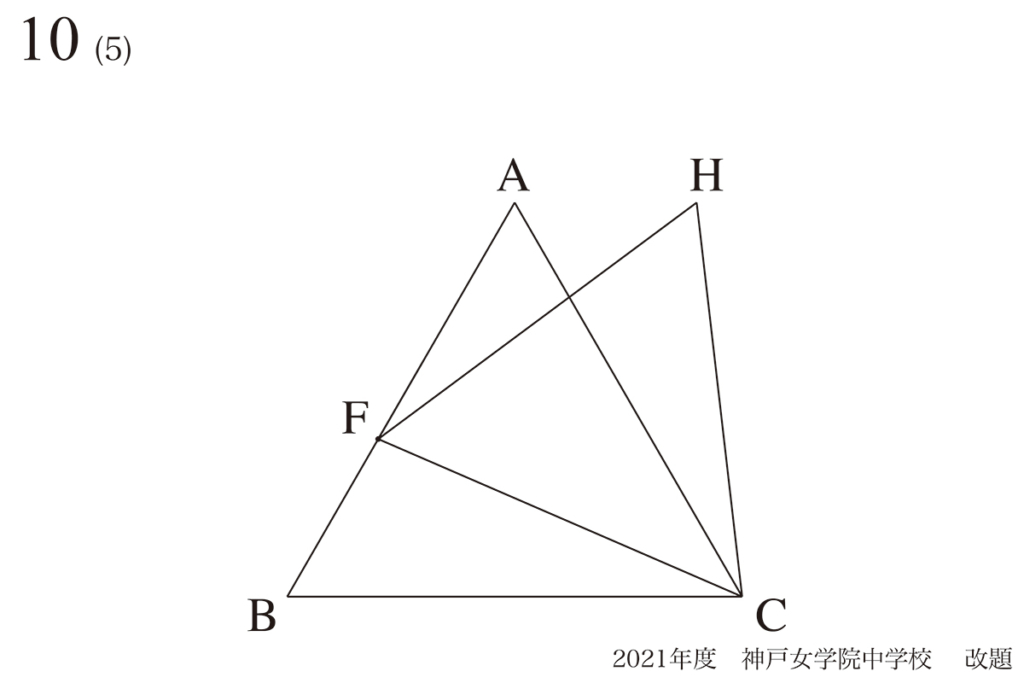
グラフを描く・理解するのが得意になるポイント：図形の対称性
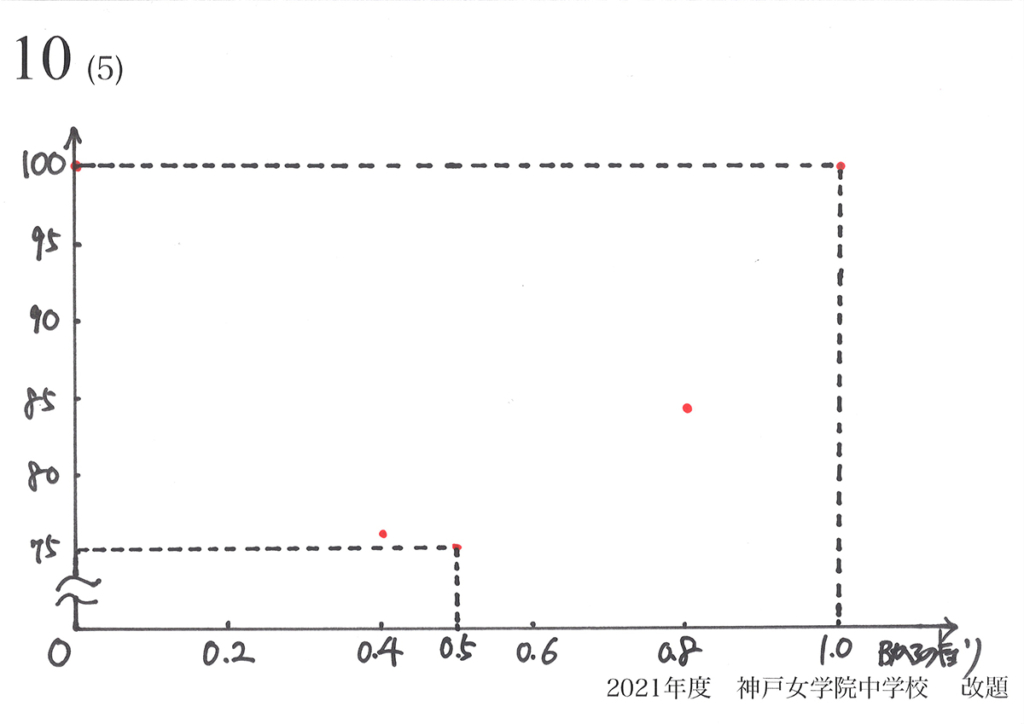
グラフの最も大事な「最大・最小の点」と分かる点をプロットしました。
・最も大きな特徴である「最大・最小」を把握
・グラフの直線・曲線の大体の雰囲気と傾向を把握
ここからは、グラフの大体の形・概形を考えてみましょう。
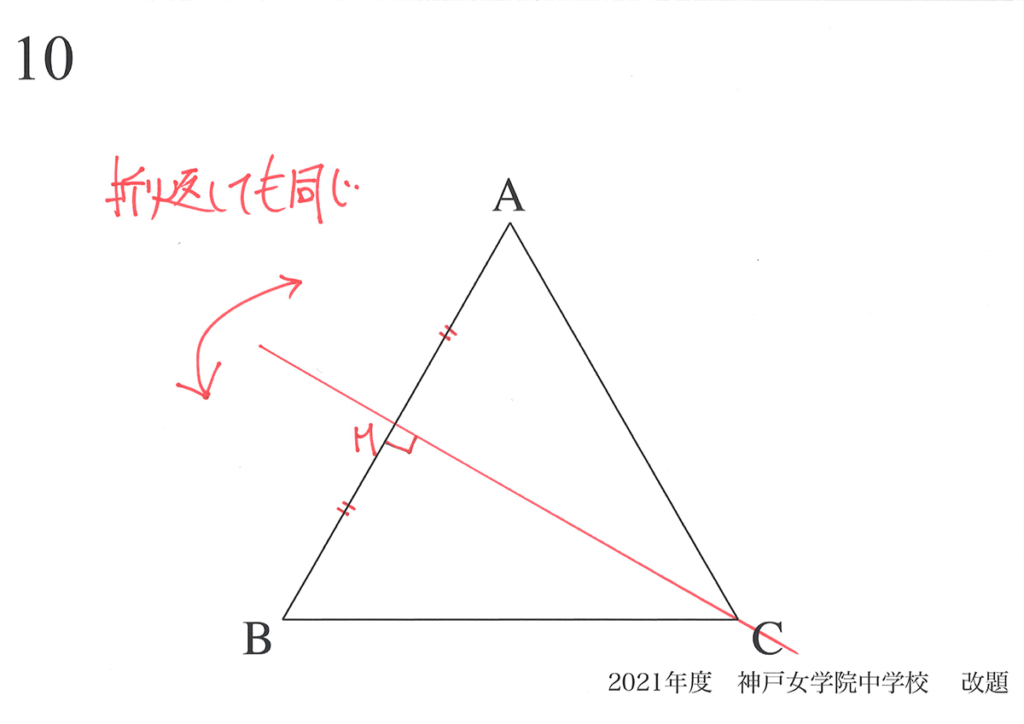
正三角形は「軸に対して対称性がある」図形です。
・ある線で折り返すと、きれいに折り返せる（折り返したら同じ）
・対称性のある図形には、様々な特徴（辺の長さが等しい、角度が等しい）がある
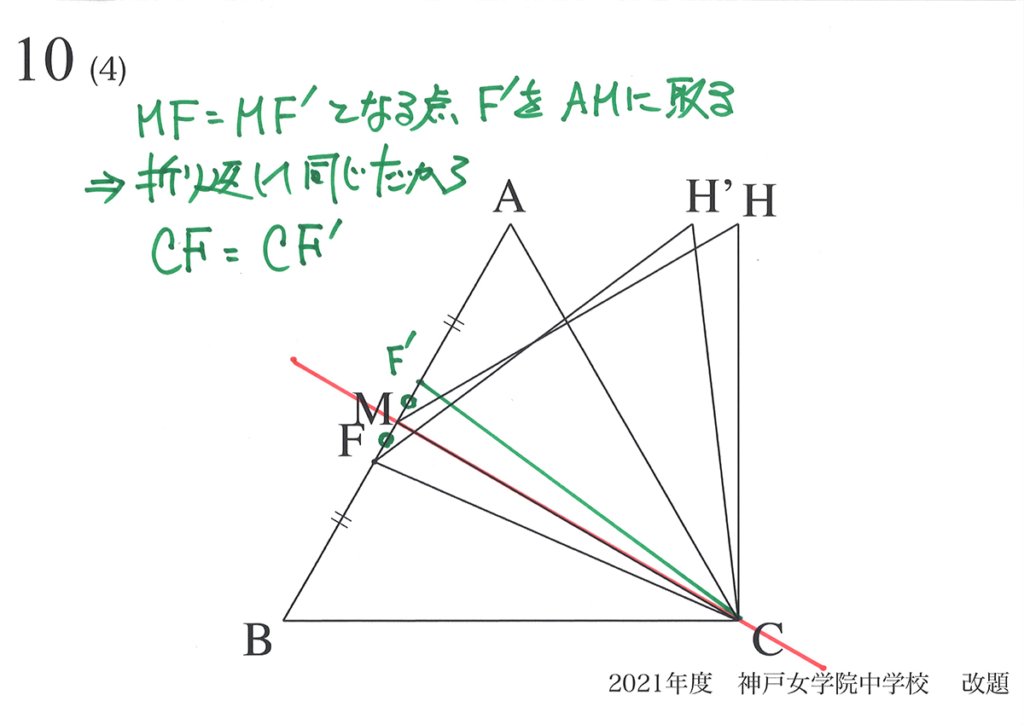
そして、「対称性がある」ので、動く点Fの位置が「BMの時とCMの時で同じ」はずです。
女子小学生「折り返したら同じ」だから、
「面積も同じ」はずだね！
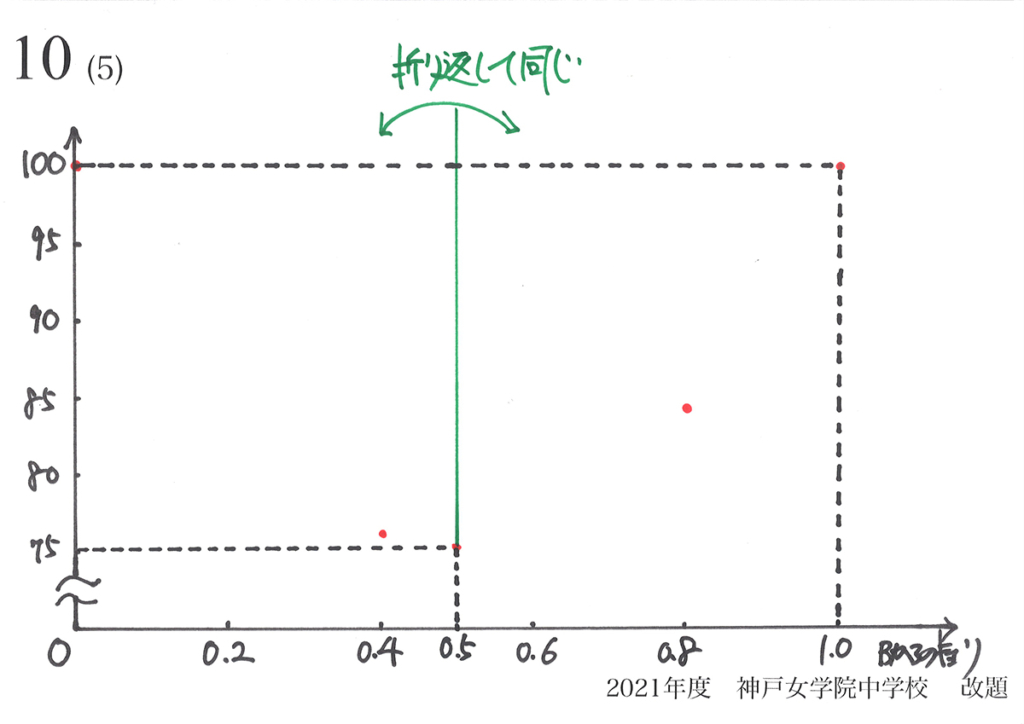
図形の対称性から、「グラフも対称性を持つ」ことがわかります。
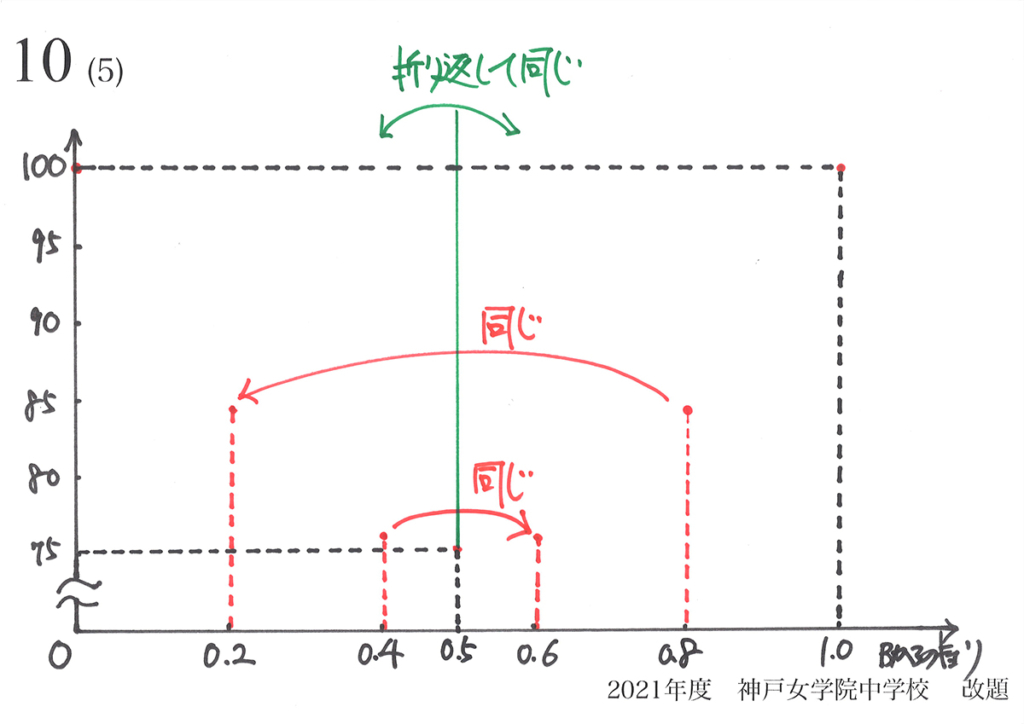
グラフも対称性を持つ、つまり「折り返して同じになるはず」です。
横軸の「ABの中点M =Bからの距離0.5」のところで、「折り返すと同じ」になります。
男子小学生さっきまで、最大・最小の3点と
他の2点で合計5点分わかっていたけど・・・
男子小学生「同じ」を考えると
「面積が分かる点」が2点増えたね！
女子小学生これで、
グラフの大体の形が分かるね！
これで、大体の感じが掴めました。
点をつないでグラフを描く：状況をイメージ
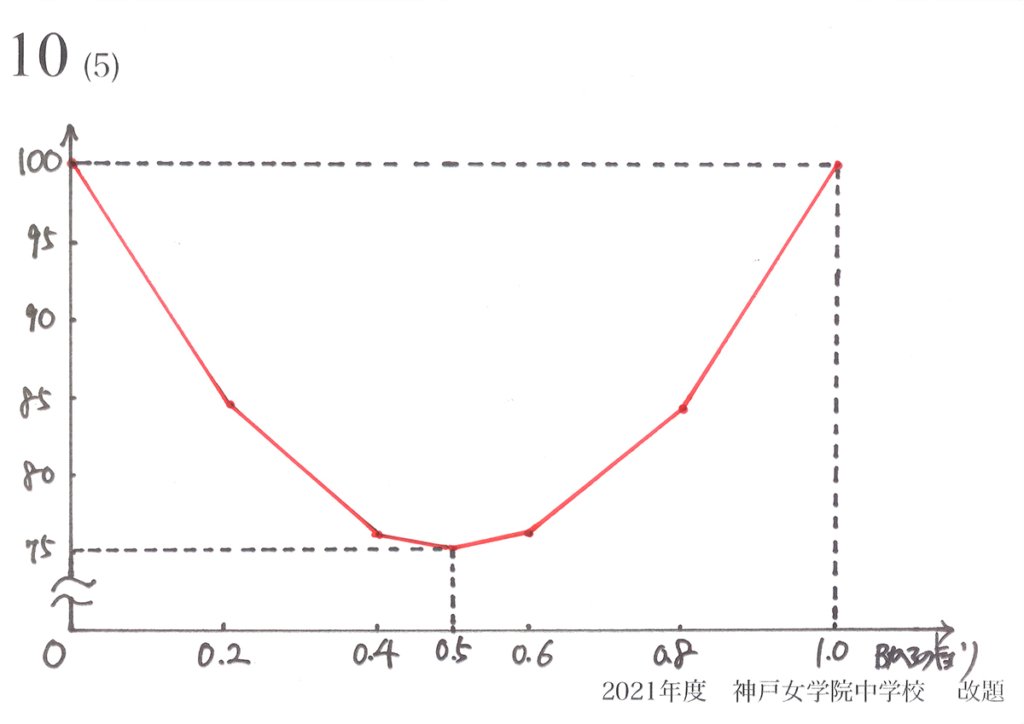
グラフの大体の形を描けば良いので、これらの7つの点をつないでみましょう。
点同士を直線で繋ぐと、上のグラフのようになります。
このグラフは小学校で習った「折れ線グラフ」ですね。
男子小学生これで
出来たね！
実は、このような「折れ線グラフ」の形にはなりません。
男子小学生えっ、
ダメなの？
「明確な間違い」ではありませんが、「大体の形」からはちょっと違います。
「直線で繋いだ点同士」のところを考えてみましょう。
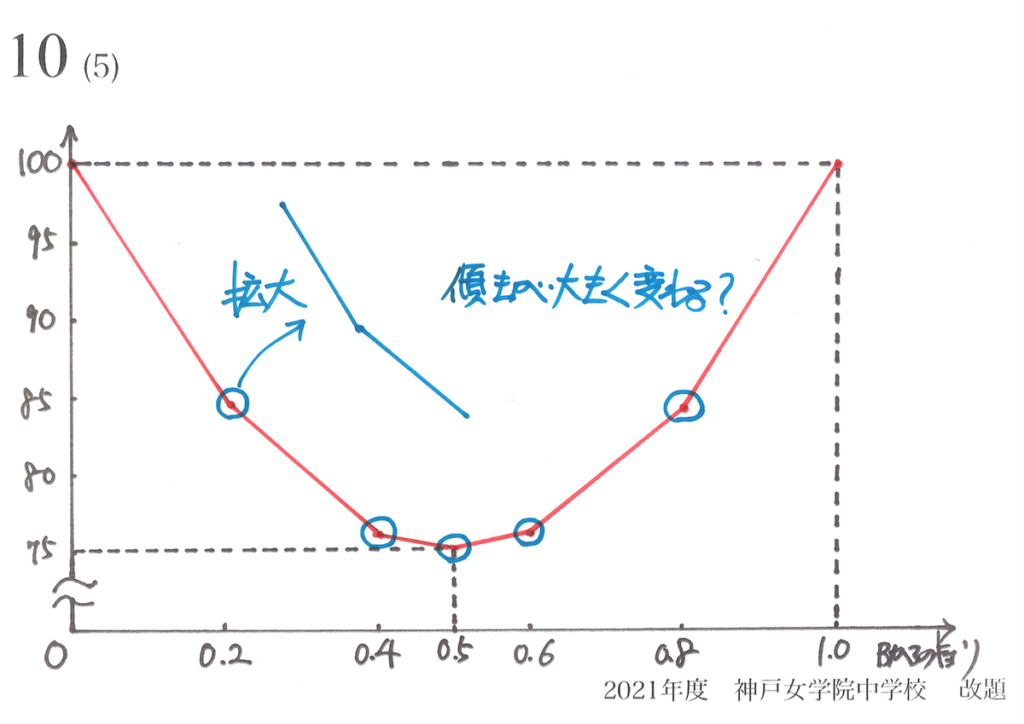
男子小学生ちょっとカックンカックン
してるね。
女子小学生ちょっと
変な感じがする・・・
矢印の話で考えた時に、正三角形FCHがどのようにできてゆくか、もう一度考えてみましょう。
問題にある「辺ABの5等分の点」で、大きな変化があるグラフになっています。
この「グラフの大体の形を描く」ことの一つの大事なポイントである「対称性」が表現されています。
そのため中学受験で出題される場合は、「ここまでで十分」という考え方もあります。
女子小学生理科実験のグラフとかは、
なめらかな曲線になるね・・・
男子小学生でもさ、これは算数の問題で
実験ではないよ。
女子小学生そうよねえ・・・
でも、同じ感じになりそうな気がするけど・・・
男子小学生確かに「カックンカックン」は
ちょっと変な感じだね・・・
実験ではありませんが、「正三角形が出来てゆく状況」を考えてみましょう。
男子小学生「状況を考える」って、
実験みたいだね！
「大体の形」をもう少し、考えてみましょう。
続きの話は、次回（下記リンク）ご紹介します。
