前回は「回路のわかりやすい考え方 3〜回路全体をイメージ・回路を難しく考えない姿勢・電気が「難しい」「出来ない」から「出来る」へ〜〜」の話でした。
回路全体をイメージ：流れる電流
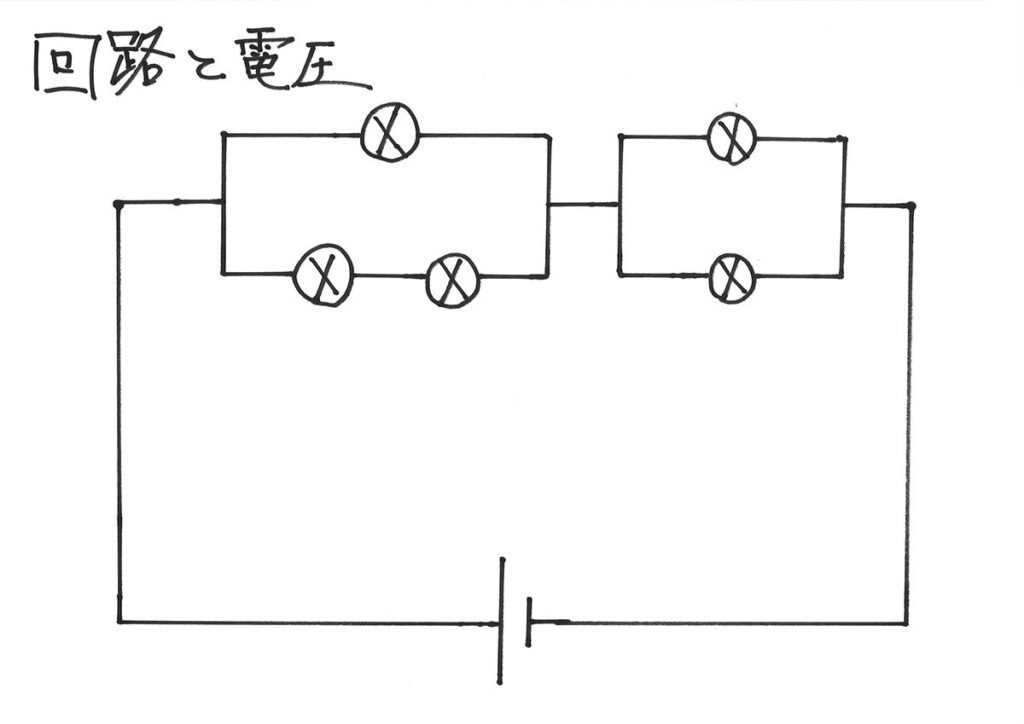
公式の「合成抵抗」を計算して、電流を求めることが多い「回路」の問題。
今回は、一つ一つ「流れる電流」と「それぞれの閉じた回路の電圧」を考えました。
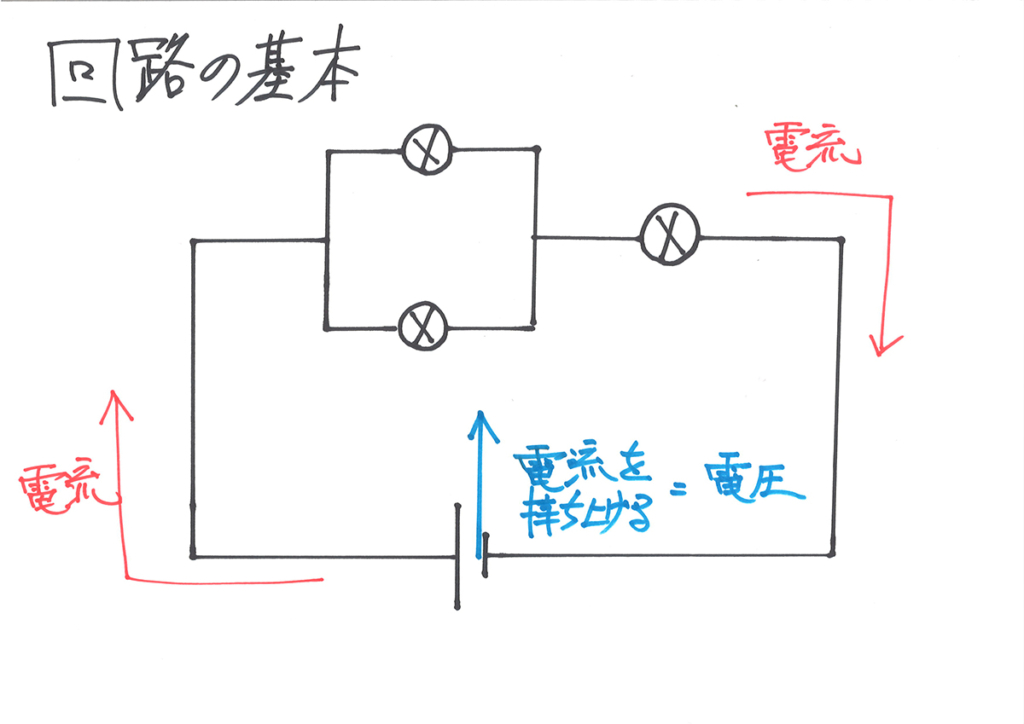
電池が電流をエイッと持ち上げて（起電力・電圧）が、グルッと回路を回ります。
流れる電流を実際に描いて、回路の中を別れたり、合流したりする電流を描きました。
「電気の流れ」である電流は、「水の流れ」である水流と同じようなイメージです。
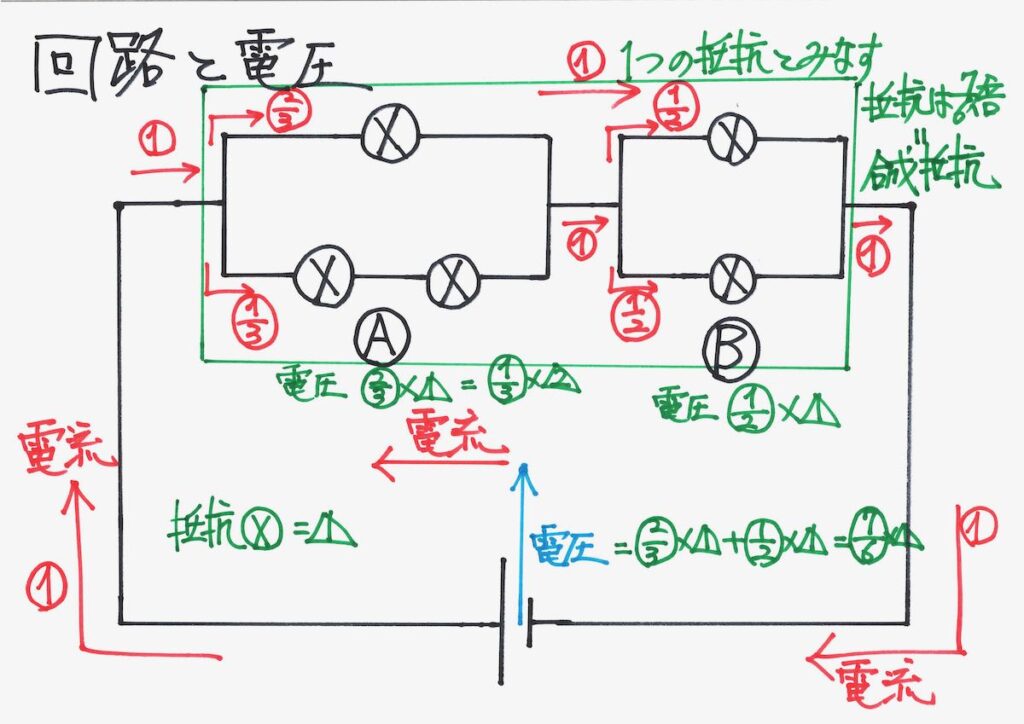
そして、回路全体の電流・電圧が全て分かりました。
基本回路（電池・電流1つ）と比較
回路を流れる電流・電圧の全容が分かりました。
今回は、合成抵抗を考えてみましょう。
「合成抵抗」という言葉が
難しく感じる・・・
公式は
暗記したよ！
「合成抵抗」というと、確かに「難しそうな」言葉です。
名前の通り「合成した」だけで、「抵抗をまとめる」とイメージしましょう。
公式を暗記した方も多いと思いますが、今回は「合成抵抗を公式ではなく、計算して」求めましょう。
今回は、基本的回路ですが、少し複雑な回路をA,Bに分けて、順次考えました。
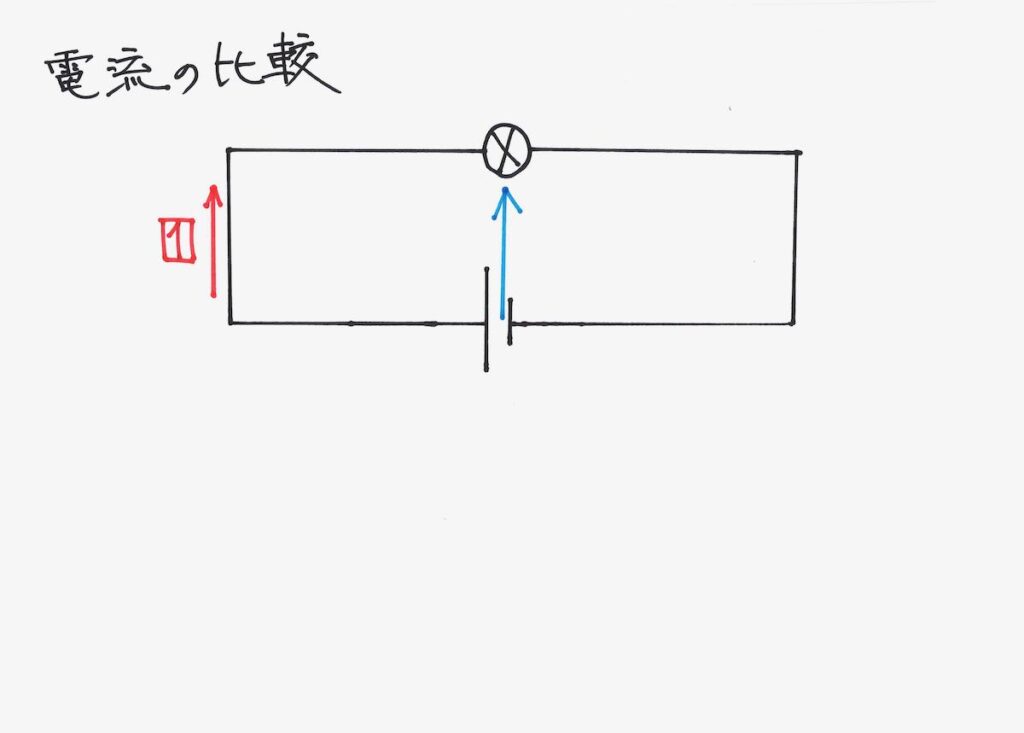
同じ電池（電圧）で、「抵抗が1つだったら、どうなるか」を考えます。
上記のような回路の場合、すぐに分かります。
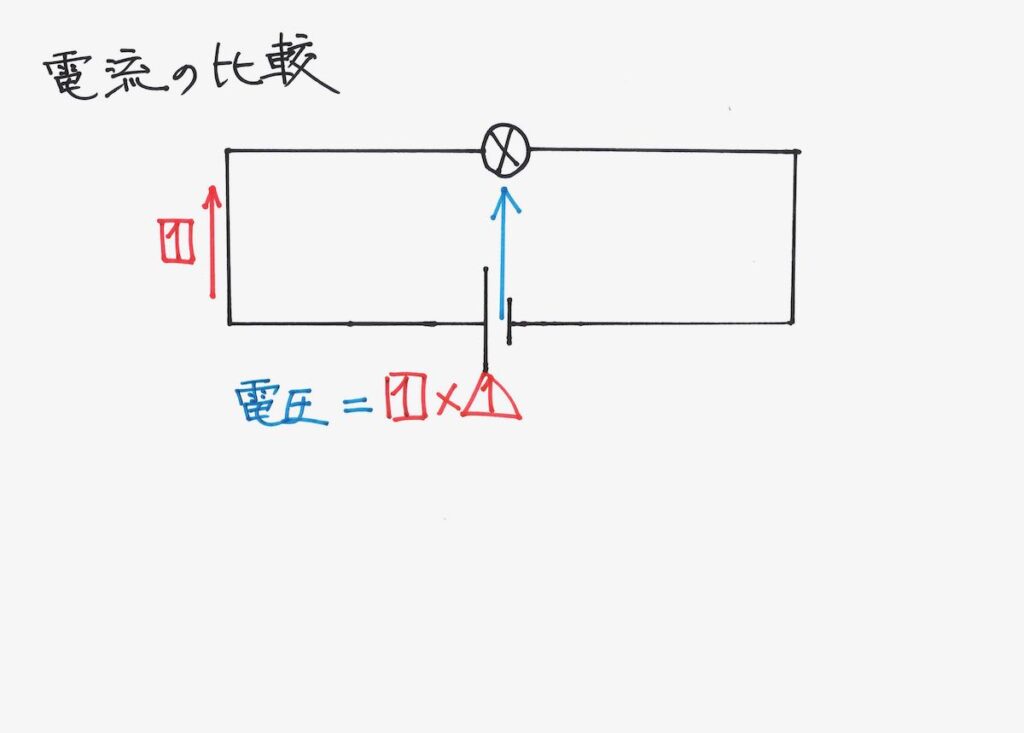
これを「基本回路」と呼びましょう。
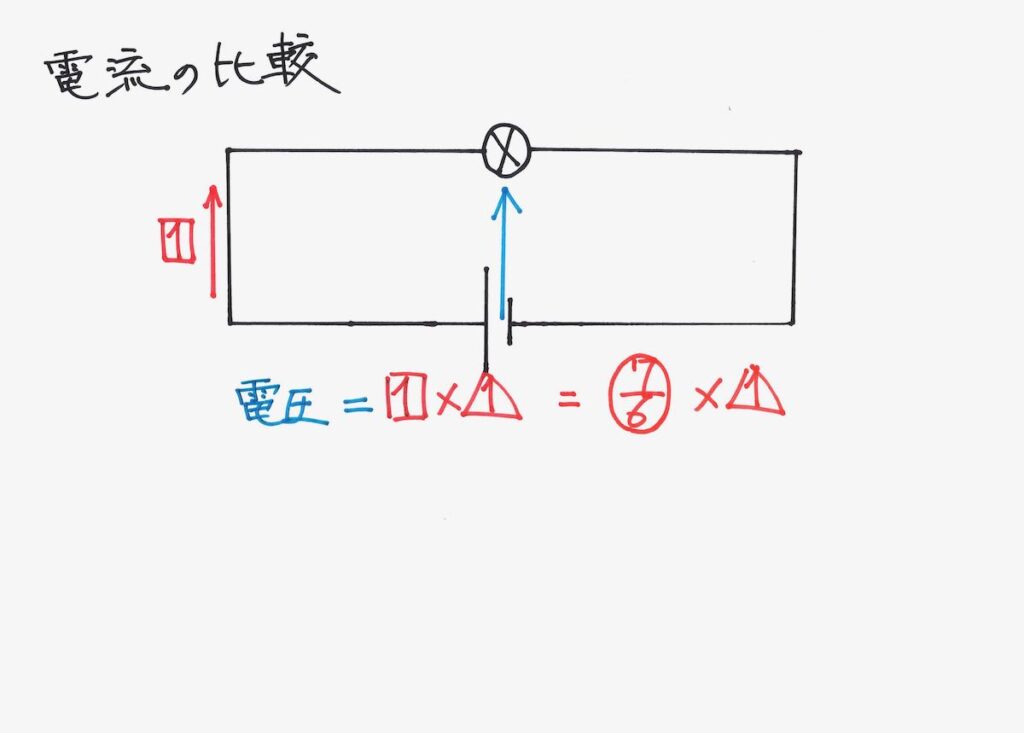
「基本回路」の電流と、先ほどの回路の電流を比較しましょう。
同じ電池（電圧）なので、等式が出来ます。
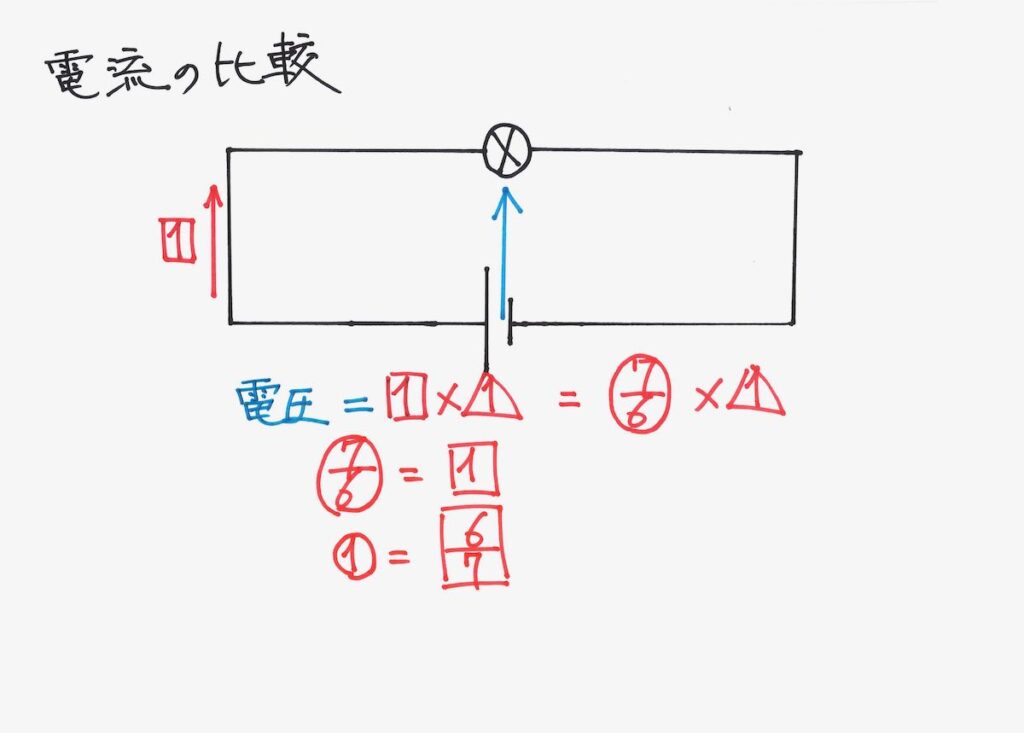
すると、「基本回路」の電流と、先ほどの回路の電流の関係式がわかります。
「電球が5個ある少し複雑な回路」と「基本回路」の全体の「電圧・起電力が同じ」が大事です。
これで、
二つの回路の間の関係が分かるね。
合成抵抗を求める：「抵抗をまとめる」イメージ
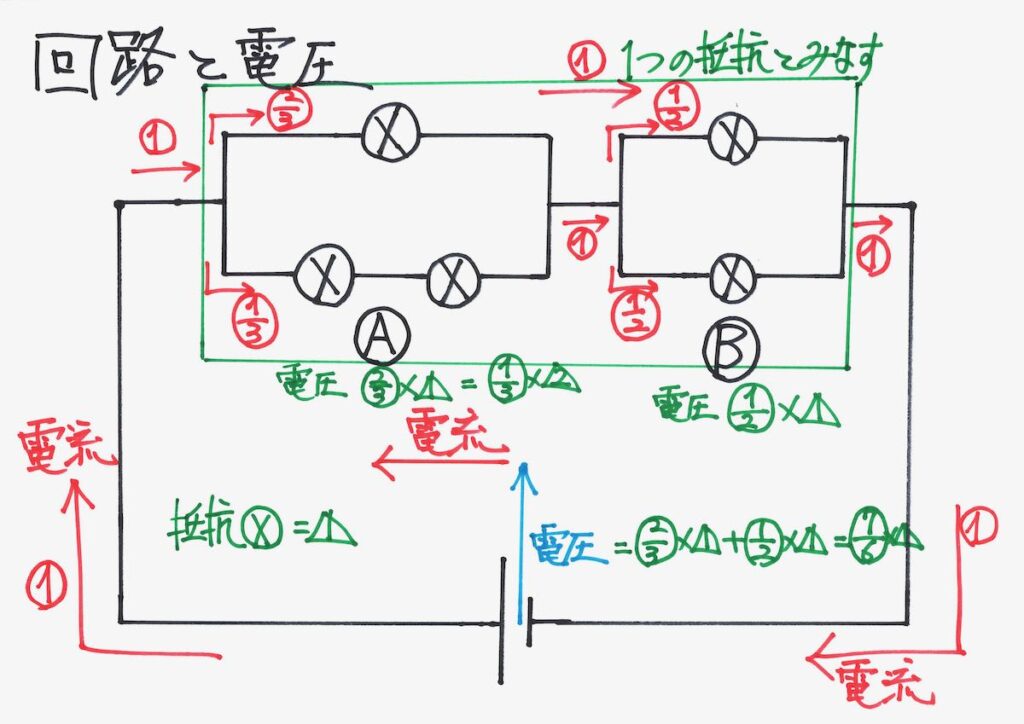
これまで考えてきた、AとBの部分をまとめて「一つの抵抗だったら」と考えましょう。
でも、
一つじゃないよね。
「まとめたら、どうなるか」をイメージしましょう。
それが「合成したら、どうなるか」です。
一つじゃないけど、
「一つになったら」と考えるんだね。
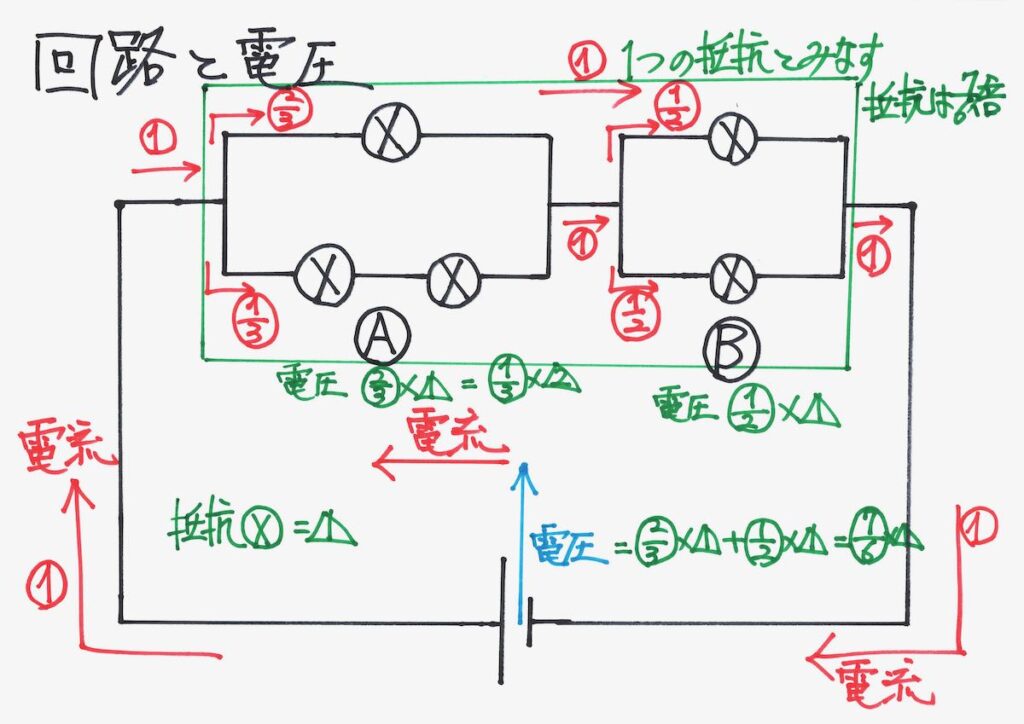
基本回路と比較すると、同じ電圧で電流が、6/7倍になりました。
そこで、電流x抵抗が同じですから、抵抗は逆数の 7/6倍になります。
この7/6を「合成抵抗」と呼びます。
これで、
合成抵抗が分かった！
こういうこと
だったのね！
・直列の抵抗：合成抵抗 R = r1 + r2
・並列の抵抗：合成抵抗 1/R = 1/r1 + 1/r2
公式の意味を考える
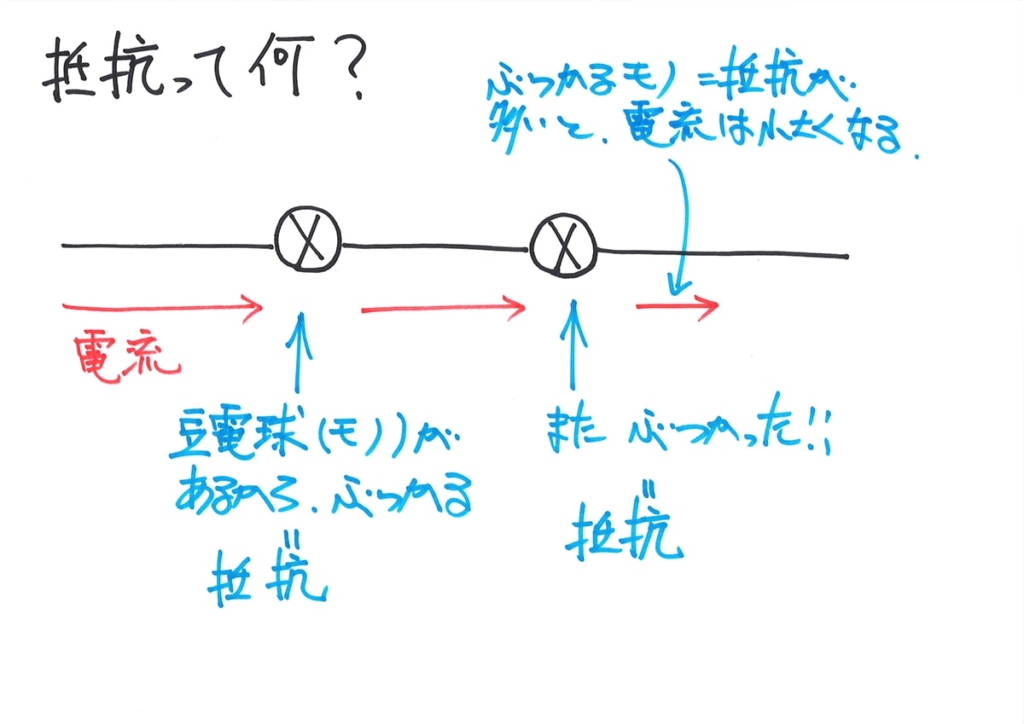
これらの直列・並列抵抗の公式は「暗記する」のが良いでしょう。
「ただ暗記」ではなく、これまで考えたような「電圧・電流を考える」姿勢があると理解が進みます。
また、「ただ暗記」ではなく、イメージを持つと良いでしょう。
「直列の抵抗」は、比較的イメージしやすいです。
直列の抵抗を流れる電流は、次々に「抵抗にぶつかる」状況になります。
そこで、「直列の抵抗 = 抵抗の和」となります。
少し難しいので、「並列の抵抗の合成抵抗」です。
「逆数（1/A)の和を計算して、さらに逆数」というのが、少し難しく感じます。
分かる、と言えば分かるけど、
ちょっと難しい・・・
「逆数」は「分数の一つ」なので、難しく感じないようにしましょう。
並列で「逆数」が出てくるのは、これまで考えた「並列の電流は、抵抗の逆数」だからです。
下がる電圧（電圧降下）が
同じだからだね。
「逆比の電流に分かれて、合流する」電流に対して、その「電流の抵抗=合成抵抗」になります。
そうか！
だから、「抵抗の逆数」を足すんだね。
「逆数を足す（和をとる）」のが難しく感じるかも知れませんが、「逆数比の電流が合流」します。
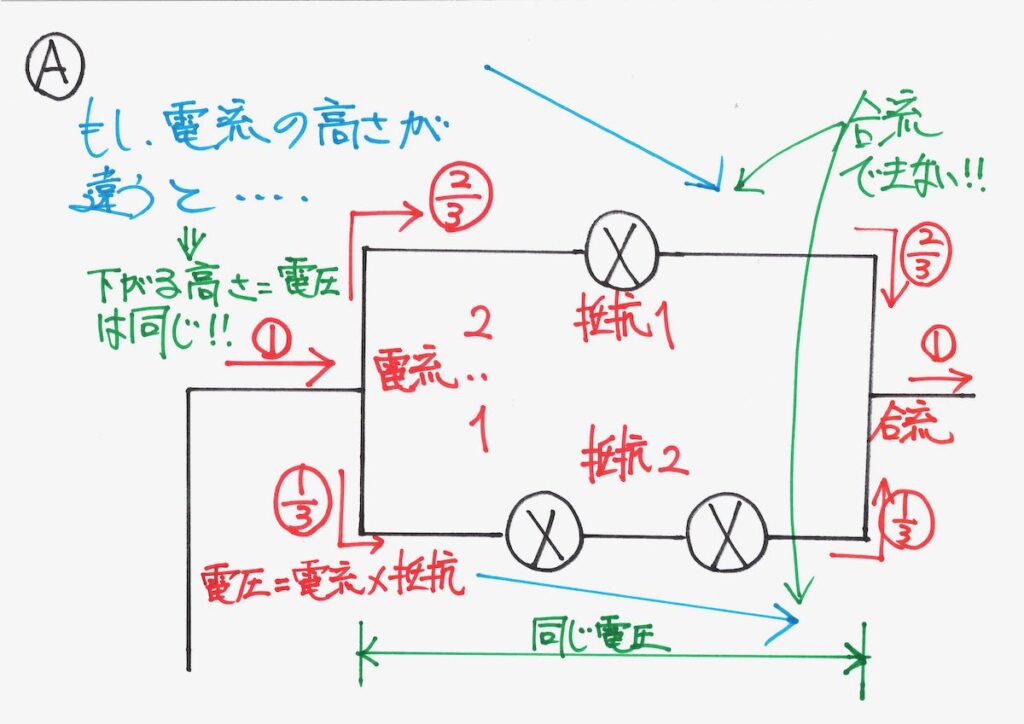
この「電圧(V)が主役」で「分かれ、合流する電流( I = V / R )」をしっかりイメージしましょう。
すると、どんな回路でも解けるようになります。
どんなに複雑な回路になっても、これまで考えたように「電流の流れ・電圧」を考えましょう。
そして、その次に「合成抵抗」などを考えるようにしましょう。
・電圧が主役：電圧降下は同じ
・電流(I = V /R )が回路全体を流れ、分流・合流するイメージ
・このイメージを持った後に、合成抵抗など計算して、電流・明るさを考える
「まず合成抵抗」と考えると、
あれっ、
合成抵抗求めたら、どうなるんだっけ？
となってしまうこともあるでしょう。
電気に限らず、理科・算数・数学では「まず公式」ではなく「状況をイメージして、公式」が大事です。
公式をたくさん覚えることも大事ですが、「公式をどう使うか」をしっかり理解しましょう。
公式を理解する大事さ
「公式を考える・理解する大事さ」をご紹介しました。
理科も同様で、電気・かっ車などの「公式」は理解しましょう。
電気は、基本を学んだ後に
合成抵抗は、
この逆数とこの逆数を足して・・・
そして、最後に逆数にすると
求まります！
と教わることも多いかと思います。
「こうすれば求まります」は、試験では有用ですが、最も大事な「理科への好奇心」が失われます。
公式を使うと「パパッとできる問題」もあります。
上記のように「基本・原理をしっかり考える」と、全ての問題が解けるようになるでしょう。
理科はイメージして、描いて、全体を理解するようにしましょう。
複雑な回路の問題も慣れると「抵抗と電流の関係」から、短い時間で全容が把握できるようになります。
それには、最初は描いて、しっかりイメージが大事です。
次回は下記リンクです。
