前回は「てんびん算のコツ・混ぜる・解き方 1〜3つの食塩水の絵を描く・「食塩水を混ぜる」とは・食塩水を理解・てんびん算の「つりあい」・食塩水=食塩+水・食塩水を分解〜」の話でした。
描いて気づくこと:3つの食塩水
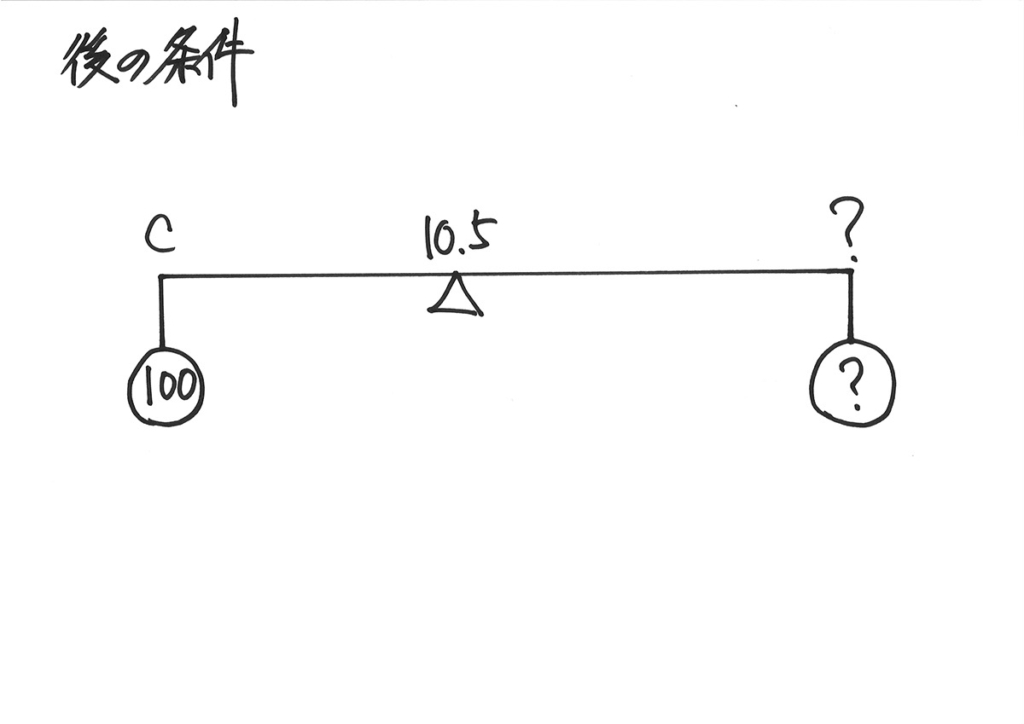
濃度も重さも不明なため、てんびんの「つり合い」が不明で進みません。
ここで、「混ぜて半分にする」ことの本質を考えましょう。
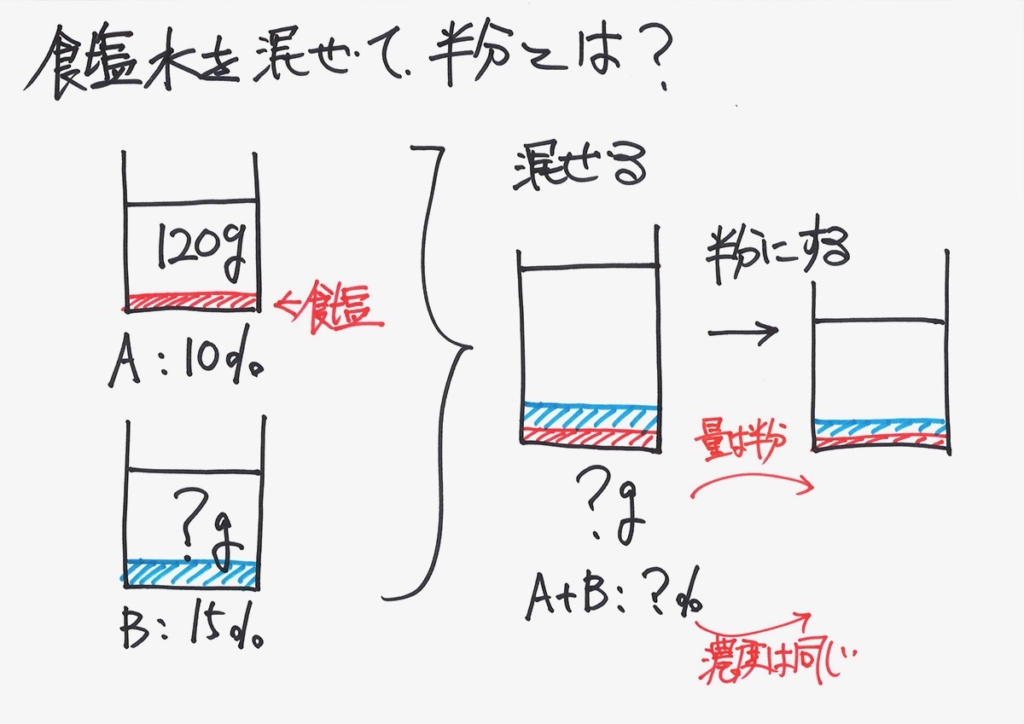
食塩水は、「水に食塩が溶けている」状況ですが、元々は「水と食塩が混ざっている」のです。
 男子小学生
男子小学生確かに、元々は
水と食塩だね。
算数でも理科でも、「混ぜる」などの時は、「混ぜるものは、そもそも何か?」を考えましょう。
食塩水を混ぜる:食塩と水を分離して描く
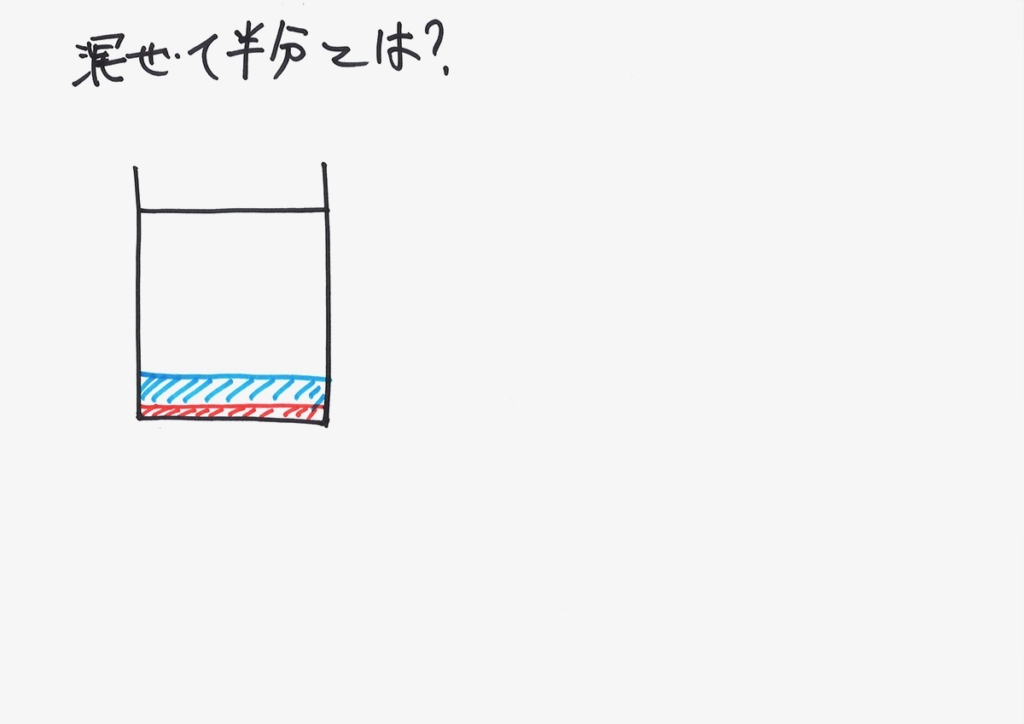

もう一度、「混ぜて半分」を考えましょう。
AとBを混ぜると、本来は、食塩水の中の食塩は「もともとAかBか?」は分からなくなります。



そう・・・
混ざってしまうからね・・・
ここでは、上のように、AとBの食塩水の「水と食塩を分離して」描いてみましょう。



これは、食塩水では、
ないのではないの?



溶けている食塩を
勝手に分離していいの?
「食塩水のイメージ」として、分離して描きました。



間違っては、
なさそうだね。



食塩が溶けないで、沈澱すれば、
この絵のようになるかも・・・
「食塩水に溶ける食塩の量」は、水の温度などで変化します。
理科で、そういう問題があるかもしれませんが、ここでは「食塩が全部溶けないで沈澱」のイメージです。
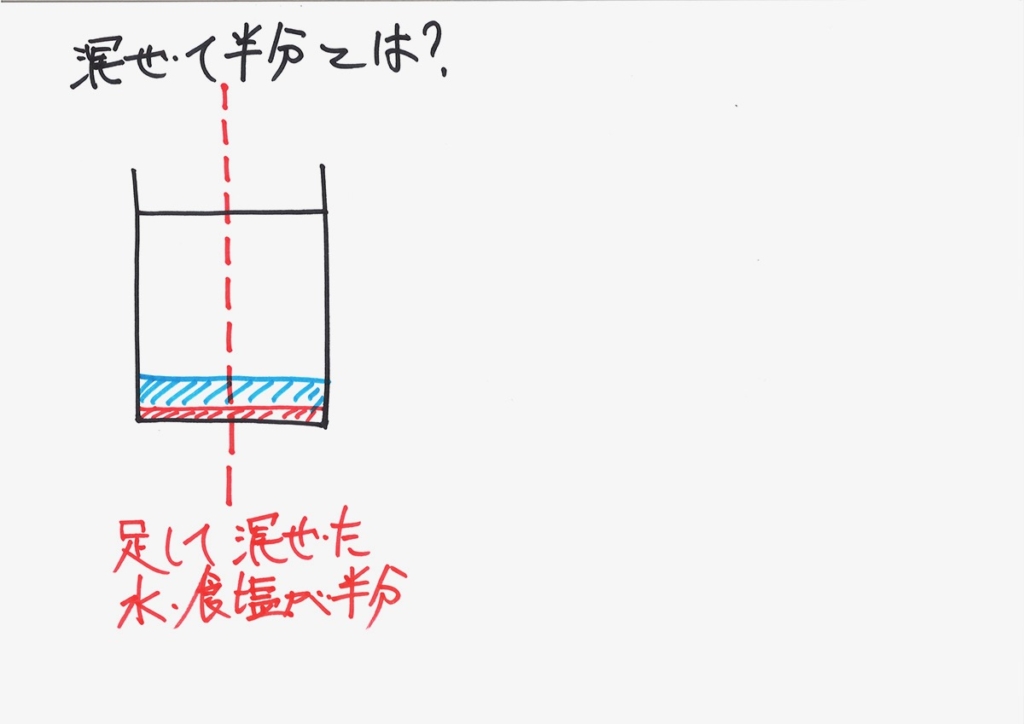

「AとBを足して、混ぜた半分」を考えますが、上の図のように実際に半分にしてみましょう。
紙の上で半分に:「頭の中」の世界は自由
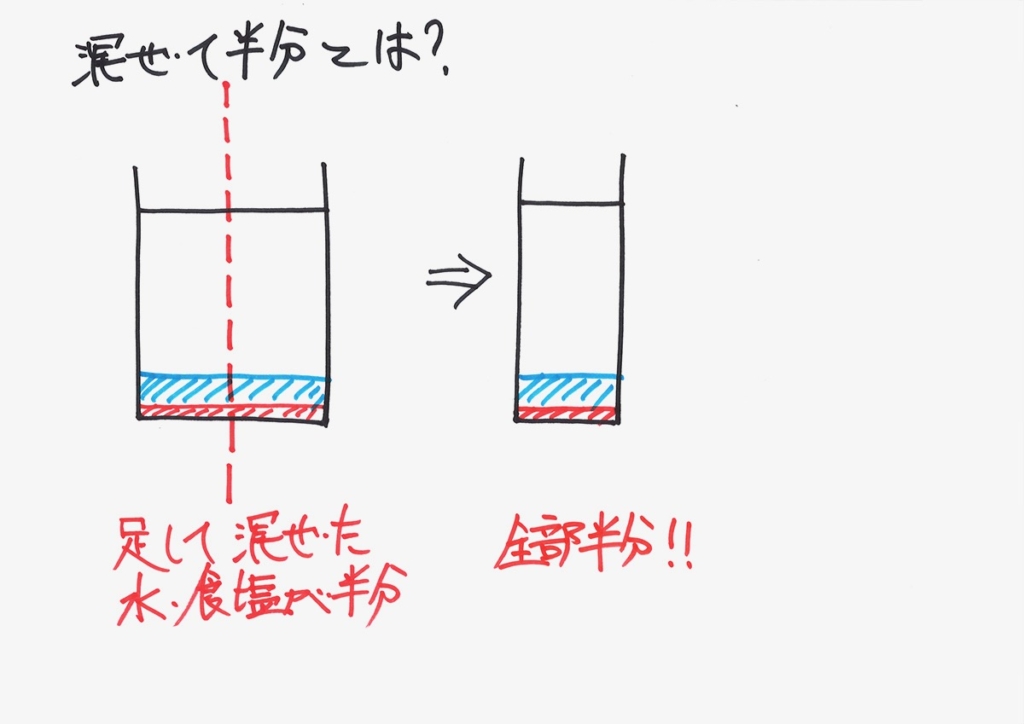

食塩水とビーカーを、実際に「縦にバサっと切る」ことは、とても難しいです。
「縦にバサっと切る」ことが出来ても、食塩水がこぼれてしまいます。



「切る」ことが難しくて、
食塩水がこぼれるなら、やっちゃダメじゃないの?
紙の上で、頭の中では可能です。



確かに
「頭の中」なら出来るけど・・・
そこで、「紙の上・頭の中のイメージ」として、考えましょう。



全部
半分になるね。



あれ?
ということは・・・



ひょっとして・・・
水と食塩は・・・
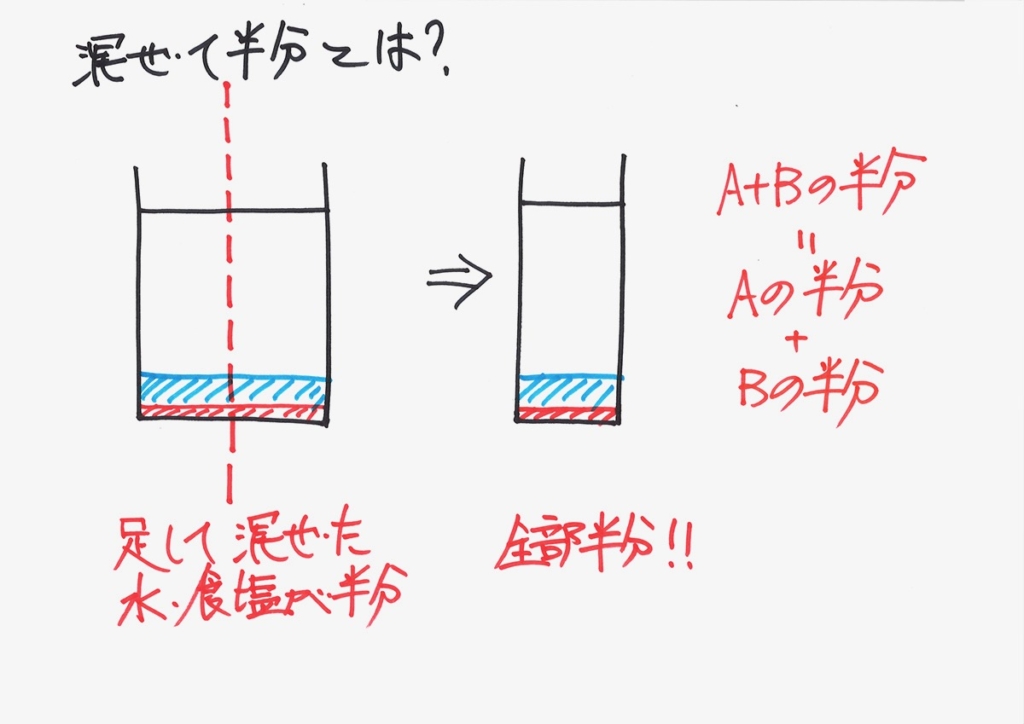




確かに、水も食塩も
半分になるね!



これなら
少し分かりそう!
描いてみたら、大事なことが分かりました。



でも、ちょっと
ピンとこないかも・・・
「ピンとこない」ようでしたら、、水も「Aの水」と「Bの水」を分けて描いてみましょう。
「AとBを混ぜて半分」とは「Aの半分とBの半分を混ぜる」と同じことです。
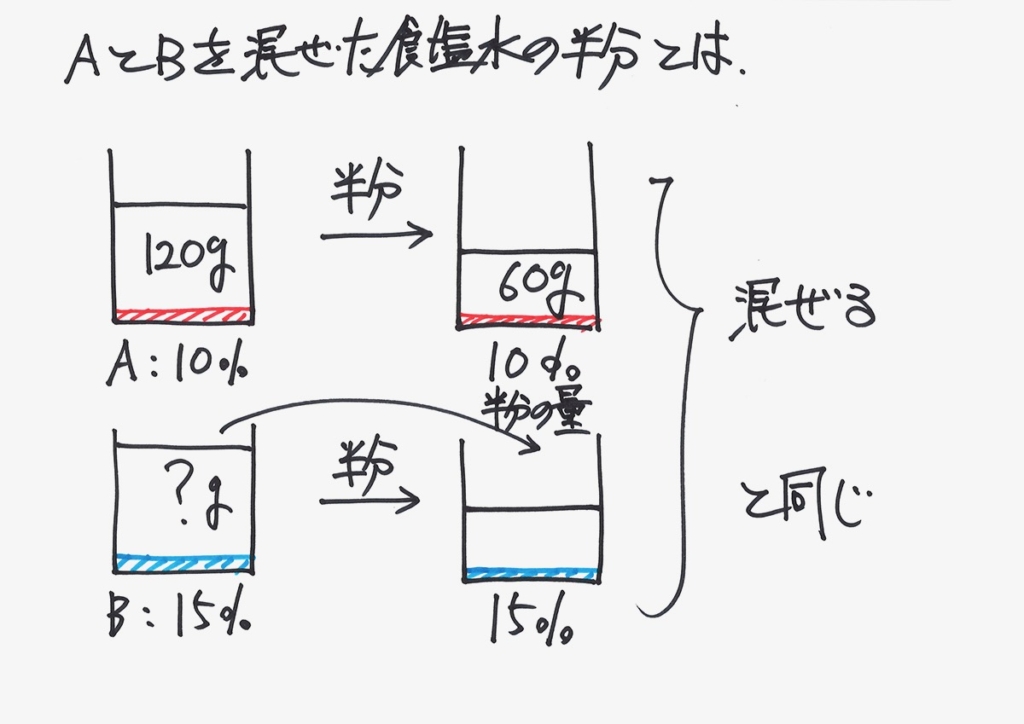




うん。
確かにそうだ!



描いてイメージしたら、
分かる!
「混ぜて半分」は「半分にして混ぜる」と同じことであることは、本質的な話です。
「混ぜて、後で半分」と「先に半分して、混ぜる」が同一であるイメージを持ちましょう。
このイメージは、算数・理科の様々な考え方にも有効な面があるでしょう。



なんか、
面白いね。



こうして描いてみるって、
大事だね!
このように、「描くと気づくこと」があります。
これらは、「頭で考えていても、なかなか分からないこと」です。
理科の「かっ車」などを描いて学ぶ話を、上記リンクでご紹介しています。



これなら、てんびん算で
出来るかも。
この考え方で、この問題を、てんびん算で考えてみましょう。
てんびん算での解く考え方は、次回ご紹介します。
次回は下記リンクです。



